پیشتر در مجموعه آموزشهای ریاضی مجله فرادرس، با مفهوم انتگرال آشنا شدیم. همچنین، مباحثی مانند انتگرال توابع مثلثاتی ، انتگرال توابع لگاریتمی و انتگرال توابع رادیکالی را ارائه کردیم. در این آموزش، درباره انتگرال توابع نمایی بحث خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
توابع نمایی و لگاریتمی در مواردی مانند مدلسازی رشد جمعیت، رشد سلول، رشد اقتصادی، توصیف فروپاشی رادیواکتیو، مصرف منابع و چندین مورد دیگر کاربرد فراوانی دارند.
انتگرال توابع نمایی
تابع نمایی یکی از توابع مهم است که در عملیاتهای ریاضی بسیار با آن سر و کار داریم. مشتق و انتگرال تابع نمایی y = e x y = e ^ x y = e x
با استفاده از فرمولهای زیر میتوان از توابع نمایی انتگرال گرفت:
∫ e x d x = e x + C \large ∫ e ^ x \, d x = e ^ x + C ∫ e x d x = e x + C
∫ a x d x = a x ln a + C \large ∫ a ^ x \, d x = \dfrac { a ^ x } { \ln a } + C ∫ a x d x = ln a a x + C
مثال ۱
پادمشتق تابع نمایی e − x e^{−x} e − x
حل: از تغییر متغیر u = − x u = - x u = − x d u = − 1 d x d u = - 1 d x d u = − 1 d x d u du d u − 1 -1 − 1 − d u = d x -du=dx − d u = d x
∫ e − x d x = − ∫ e u d u = − e u + C = − e − x + C . \large ∫ e ^ { − x } \, d x = − ∫ e ^ u \, d u = − e ^ u + C = − e ^ { − x } + C . \nonumber ∫ e − x d x = − ∫ e u d u = − e u + C = − e − x + C .
یک اشتباه رایج در هنگام محاسبات مربوط به نماییها این است که با نمایی e e e e e e
مثال ۲
پادمشتق تابع نمایی e x 1 + e x e^x\sqrt{1+e^x} e x 1 + e x
حل: ابتدا توان را به صورت یک عدد گویا مینویسیم:
∫ e x 1 + e x d x = ∫ e x ( 1 + e x ) 1 / 2 d x . \large ∫ e ^ x \sqrt { 1 + e ^ x } \, d x = ∫ e ^ x ( 1 + e ^ x ) ^ { 1 / 2 } \, d x . \nonumber ∫ e x 1 + e x d x = ∫ e x ( 1 + e x ) 1/2 d x .
با استفاده از تغییر متغیر u = 1 + e x u=1+e^x u = 1 + e x d u = e x d x du=e^x\,dx d u = e x d x
∫ e x ( 1 + e x ) 1 / 2 d x = ∫ u 1 / 2 d u . \large ∫ e ^ x ( 1 + e ^ x ) ^ { 1 / 2 } \, d x = ∫ u ^ { 1 / 2 } \, d u . \nonumber ∫ e x ( 1 + e x ) 1/2 d x = ∫ u 1/2 d u .
در نتیجه:
∫ u 1 / 2 d u = u 3 / 2 3 / 2 + C = 2 3 u 3 / 2 + C = 2 3 ( 1 + e x ) 3 / 2 + C \large ∫ u ^ { 1 / 2 } \, d u = \dfrac { u ^ { 3 / 2 } }{ 3 / 2 } + C = \dfrac { 2 } { 3 } u ^ { 3 / 2 } + C = \dfrac { 2 } { 3 } ( 1 + e ^ x ) ^ { 3 / 2 } + C \nonumber ∫ u 1/2 d u = 3/2 u 3/2 + C = 3 2 u 3/2 + C = 3 2 ( 1 + e x ) 3/2 + C
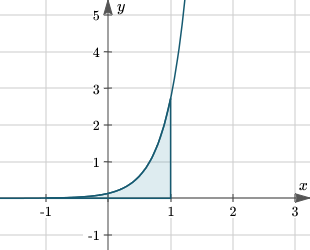
شکل ۱ مثال ۳
حاصل انتگرال ∫ 3 x 2 e 2 x 3 d x \displaystyle ∫3x^2e^{2x^3}\,dx ∫ 3 x 2 e 2 x 3 d x
حل: توان تابع نمایی را به عنوان u = 2 x 3 u=2x^3 u = 2 x 3 d u = 6 x 2 d x du=6x^2\,dx d u = 6 x 2 d x 3 x 2 3 x ^ 2 3 x 2 6 x 2 6 x ^ 2 6 x 2 1 2 \dfrac{1}{2} 2 1 u u u x x x
∫ 3 x 2 e 2 x 3 d x = 1 2 ∫ e u d u . \large ∫ 3 x ^ 2 e ^ { 2 x ^ 3 } \, d x = \frac { 1 } { 2 }∫ e ^ u \, d u . ∫ 3 x 2 e 2 x 3 d x = 2 1 ∫ e u d u .
با انتگرالگیری از عبارت برحسب u u u x x x
1 2 ∫ e u d u = 1 2 e u + C = 1 2 e 2 x 3 + C . \large \frac { 1 } { 2 } ∫ e ^ u \, d u = \frac { 1 } { 2 } e ^ u + C = \frac { 1 } { 2 } e ^ 2 x ^ 3+ C . 2 1 ∫ e u d u = 2 1 e u + C = 2 1 e 2 x 3 + C .
مثال ۴
انتگرال معین زیر را با استفاده از تغییر متغیر حل کنید:
∫ 1 2 e 1 / x x 2 d x . \large ∫ ^ 2 _ 1 \dfrac { e ^ { 1 / x } } { x ^ 2 } \, d x . \nonumber ∫ 1 2 x 2 e 1/ x d x .
حل: باید مسئله را بازنویسی کنیم. ابتدا نمایی را طوری مینویسیم که x x x x 2 x ^ 2 x 2
∫ 1 2 e 1 / x x 2 d x = ∫ 1 2 e x − 1 x − 2 d x . \large ∫ ^ 2 _ 1 \dfrac { e ^ { 1 / x } }{ x ^ 2 } \, \, d x = ∫^ 2 _ 1 e ^ { x ^ { − 1 } } x ^ { − 2 } \, d x . \nonumber ∫ 1 2 x 2 e 1/ x d x = ∫ 1 2 e x − 1 x − 2 d x .
توان نمایی را u = x − 1 u=x^{−1} u = x − 1
d u = − x − 2 d x \large d u = − x ^ { −2 } \, d x \nonumber d u = − x − 2 d x
− d u = x − 2 d x . \large − d u = x ^ { − 2 } \, d x . \nonumber − d u = x − 2 d x .
با بیرون آوردن علامت منفی، مسئله به صورت زیر خواهد بود:
− ∫ e u d u . \large − ∫ e ^ u \, d u . \nonumber − ∫ e u d u .
بنابراین، حدود انتگرال به صورت زیر تغییر خواهند کرد:
u = ( 1 ) − 1 = 1 \large u = ( 1 ) ^ { − 1 } = 1 \nonumber u = ( 1 ) − 1 = 1
u = ( 2 ) − 1 = 1 2 . \large u = ( 2 ) ^ { − 1 } = \dfrac { 1 } { 2 } . \nonumber u = ( 2 ) − 1 = 2 1 .
در نهایت، انتگرال به صورت زیر محاسبه میشود:
− ∫ 1 1 / 2 e u d u = ∫ 1 / 2 1 e u d u = e u ∣ 1 / 2 1 = e − e 1 / 2 = e − e . \large − ∫ ^ { 1 / 2 } _ 1 e ^ u \, d u = ∫ ^ 1 _ { 1 / 2 } e ^ u \, du = e ^ u \big | ^ 1 _ { 1 / 2 } = e − e ^ { 1 /2 } = e − \sqrt { e } . \nonumber − ∫ 1 1/2 e u d u = ∫ 1/2 1 e u d u = e u 1/2 1 = e − e 1/2 = e − e .
انتگرالهایی با لگاریتم طبیعی
انتگرالگیری از توابعی به فرم f ( x ) = 1 x f(x)=\dfrac{1}{x} f ( x ) = x 1 f ( x ) = x − 1 f(x) = x^{−1} f ( x ) = x − 1 x x x − 1 -1 − 1
∫ 1 x d x = ln ∣ x ∣ + C \large ∫ \frac { 1 } { x } \, d x = \ln | x | + C ∫ x 1 d x = ln ∣ x ∣ + C
در حقیقت، میتوانیم این فرمول را برای انتگرالدههای کسری که در آنها صورت مشتق مخرج است تعمیم دهیم. در واقع، با استفاده از قاعده زنجیرهای میتوانیم مشتق y = ln [ u ( x ) ] y = \ln[u(x)] y = ln [ u ( x )]
d d x ( ln [ u ( x ) ] ) = 1 u ( x ) ⋅ u ′ ( x ) = u ′ ( x ) u ( x ) \large \frac { d } {d x} \left ( \ln [ u ( x ) ] \right ) = \frac { 1 } { u ( x ) } \cdot u' ( x ) = \frac { u' ( x ) } { u (x ) } d x d ( ln [ u ( x )] ) = u ( x ) 1 ⋅ u ′ ( x ) = u ( x ) u ′ ( x )
بنابراین، فرمول زیر یک فرمول بسیار مهم و کاربردی در حل انتگرال است:
∫ u ′ ( x ) u ( x ) d x = ln ∣ u ( x ) ∣ + C \large ∫ \frac { u' ( x ) } { u ( x ) } \, d x =\ln | u ( x ) | + C ∫ u ( x ) u ′ ( x ) d x = ln ∣ u ( x ) ∣ + C
مثال ۵
پادمشتق تابع 3 x − 10 \dfrac { 3 } { x − 1 0 } x − 10 3
حل: ابتدا ضریب 3 3 3 u ′ / u u'/u u ′ / u
∫ 3 x − 10 d x = 3 ∫ 1 x − 10 d x = 3 ∫ d u u = 3 ln ∣ u ∣ + C = 3 ln ∣ x − 10 ∣ + C , x ≠ 10. \large ∫ \dfrac { 3 } { x − 10 } \, d x = 3 ∫ \dfrac { 1 } { x − 1 0 } \, d x = 3 ∫ \dfrac { d u } { u } = 3 \ln | u | + C = 3 \ln | x − 1 0 | + C , \quad x ≠ 1 0 . \nonumber ∫ x − 10 3 d x = 3 ∫ x − 10 1 d x = 3 ∫ u d u = 3 ln ∣ u ∣ + C = 3 ln ∣ x − 10∣ + C , x = 10.
شکل زیر نمودار تابع را نشان میدهد.
شکل ۲ مثال ۶
پادمشتق تابع زیر را به دست آورید:
2 x 3 + 3 x x 4 + 3 x 2 . \large \dfrac { 2 x ^ 3 + 3 x } { x ^ 4 + 3 x ^ 2 } . \nonumber x 4 + 3 x 2 2 x 3 + 3 x .
حل: از تغییر متغیر استفاده میکنیم. متغیر u = x 4 + 3 x 2 u=x^4+3x^2 u = x 4 + 3 x 2 d u = ( 4 x 3 + 6 x ) d x du=(4x^3+6x)\,dx d u = ( 4 x 3 + 6 x ) d x d u du d u 2 2 2
d u = ( 4 x 3 + 6 x ) d x = 2 ( 2 x 3 + 3 x ) d x \large d u = ( 4 x ^ 3 + 6 x ) \, d x = 2 ( 2 x ^ 3 + 3 x ) \, d x \nonumber d u = ( 4 x 3 + 6 x ) d x = 2 ( 2 x 3 + 3 x ) d x
1 2 d u = ( 2 x 3 + 3 x ) d x . \large \dfrac { 1 } { 2 } \, d u = ( 2 x ^ 3 + 3 x ) \, d x . \nonumber 2 1 d u = ( 2 x 3 + 3 x ) d x .
انتگرالده را برحسب u u u
∫ 2 x 3 + 3 x x 4 + 3 x 2 d x = 1 2 ∫ 1 u d u . \large ∫ \frac { 2 x ^ 3 + 3 x } { x ^ 4 + 3 x ^ 2 } \, d x = \dfrac { 1 } { 2 } ∫ \frac { 1 } { u } \, d u . \nonumber ∫ x 4 + 3 x 2 2 x 3 + 3 x d x = 2 1 ∫ u 1 d u .
بنابراین، خواهیم داشت:
1 2 ∫ 1 u d u = 1 2 ln ∣ u ∣ + C = 1 2 ln ∣ x 4 + 3 x 2 ∣ + C . \large \dfrac { 1 } { 2 } ∫ \frac { 1 } { u } \, d u = \dfrac { 1 } { 2 } \ln | u | + C = \dfrac { 1 } { 2 } \ln ∣ x ^ 4 + 3x ^ 2 ∣ + C . \nonumber 2 1 ∫ u 1 d u = 2 1 ln ∣ u ∣ + C = 2 1 ln ∣ x 4 + 3 x 2 ∣ + C .
مثال ۷
حاصل انتگرال معین زیر را به دست آورید:
∫ 0 π / 2 sin x 1 + cos x d x . \large ∫ ^ { \pi / 2 } _ 0 \dfrac { \sin x } { 1 + \cos x } \, d x . \nonumber ∫ 0 π /2 1 + cos x sin x d x .
حل: برای حل این مثال، از تغییر متغیر u = 1 + cos x u=1+\cos x u = 1 + cos x d u = − sin x d x du=−\sin x\,\,dx d u = − sin x d x u u u
u = 1 + cos ( 0 ) = 2 \large u = 1 + \cos ( 0 ) = 2 u = 1 + cos ( 0 ) = 2
u = 1 + cos ( π 2 ) = 1. \large u = 1 + \cos ( \dfrac { π } { 2 } ) = 1 . u = 1 + cos ( 2 π ) = 1.
در نتیجه، خواهیم داشت:
∫ 0 π / 2 sin x 1 + cos x = − ∫ 2 1 1 u d u = ∫ 1 2 1 u d u = ln ∣ u ∣ ∣ 1 2 = [ ln 2 − ln 1 ] = ln 2 \large \begin {align*} ∫ ^ { \pi / 2 } _ 0 \dfrac { \sin x }{ 1 + \cos x } & = − ∫ ^ 1 _ 2 \frac { 1 } { u } \, d u = ∫ ^ 2 _ 1 \frac { 1 } { u } \, d u \\ & = \ln | u | \, \bigg | ^ 2 _ 1 = [ \ln 2 − \ln 1 ] = \ln 2 \end {align*} ∫ 0 π /2 1 + cos x sin x = − ∫ 2 1 u 1 d u = ∫ 1 2 u 1 d u = ln ∣ u ∣ 1 2 = [ ln 2 − ln 1 ] = ln 2
مثال ۸
حاصل انتگرال ∫ − 1 1 d x e 2 − 3 x { \int _{ { - { 1 } } } ^ { { 1 } } } \frac { { { \left . { d } { x } \right . } } } { { { e } ^ { { { 2 } - { 3 } { x } } } } } ∫ − 1 1 e 2 − 3 x d x
حل: از آنجایی که − ( 2 − 3 x ) = 2 x − 2 -(2-3x)=2x-2 − ( 2 − 3 x ) = 2 x − 2
∫ − 1 1 e − ( 2 − 3 x ) d x = ∫ − 1 1 e 3 x − 2 d x \large { \int _ { { - { 1 } } } ^ { {1 }} } { e } ^ { {- { \left ( { 2 } -{ 3 } {x } \right ) } } } { \left . { d } { x } \right . } = { \int _ { - { { 1 } } } ^ { { 1 } } } { e } ^ { { { 3 } { x } - { 2 } } } { \left . { d } { x } \right . } ∫ − 1 1 e − ( 2 − 3 x ) d x = ∫ − 1 1 e 3 x − 2 d x
با استفاده از تغییر متغیر u = 3 x − 2 u=3x-2 u = 3 x − 2 d u = 3 d x du=3dx d u = 3 d x
∫ − 1 1 e 3 x − 2 d x = 1 3 [ e 3 x − 2 ] − 1 1 = 1 3 [ e 1 − e − 5 ] = 0.9038 \large { \int _ { - { { 1 } } } ^ { { 1} } } { e } ^ { { { 3 }{ x } - { 2 } } } { \left . { d } { x } \right . } = \frac { 1 } {{ 3 } } { { \left [ { e } ^ { { { 3 } { x } - { 2 } } } \right ] } _ { - { { 1 } } } ^ { { 1 } } } = \frac { 1 } { { 3 } } { \left [ { e } ^ { 1 } -{ e } ^ { - { { 5 } } } \right ] } = { 0 . 9 0 3 8 } ∫ − 1 1 e 3 x − 2 d x = 3 1 [ e 3 x − 2 ] − 1 1 = 3 1 [ e 1 − e − 5 ] = 0.9038
نمودار منحنی y = 1 e 2 − 3 x { y } = \frac { 1 } { { e } ^ { { { 2 } - { 3 } { x } } } } y = e 2 − 3 x 1
شکل ۳ حالتهای خاص
در این بخش، چند حالت خاص مربوط به محاسبه انتگرال توابع نمایی را بررسی میکنیم.
حالت خاص ۱: اگر انتگرال به صورت ∫ e x ( f ( x ) + f ′ ( x ) ) d x \int e ^ x \big ( f ( x ) + f' ( x ) \big ) \, d x ∫ e x ( f ( x ) + f ′ ( x ) ) d x e x f ( x ) + C e ^ x f ( x ) + C e x f ( x ) + C حالت خاص ۲: اگر انتگرال به صورت I = ∫ e a x cos ( b x + c ) I = \int e ^ { a x } \cos ( b x + c ) I = ∫ e a x cos ( b x + c )
I = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 + b 2 . \large I = \dfrac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 + b ^ 2 } . I = a 2 + b 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) .
برای اثبات این رابطه، میتوان نوشت:
I = ∫ e a x cos ( b x + c ) d x = cos ( b x + c ) e a x a + b a ∫ e a x sin ( b x + c ) d x = cos ( b x + c ) e a x a + b a ( e a x a sin ( b x + c ) − b a ∫ e a x cos ( b x + c ) ) d x = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 − b 2 a 2 I \large \begin {aligned} I & = \int e ^ { a x } \cos ( b x + c ) d x \\ & = \cos ( b x + c ) \frac { e ^ { a x } } { a } + \frac { b } { a } \int e ^ { a x } \sin ( b x + c ) d x \\ & = \cos ( b x + c ) \frac { e ^ { a x } } { a } + \frac { b } { a } \left ( \frac { e ^ { a x } } { a } \sin ( b x + c ) - \frac { b } { a } \int e ^ { a x } \cos ( b x + c ) \right ) d x \\ & = \frac { e ^ { a x } ( a \cos ( b x + c ) + b \sin ( b x + c ) ) } { a ^ { 2 } } - \frac { b ^ { 2 } } { a ^{ 2 } } I \end {aligned} I = ∫ e a x cos ( b x + c ) d x = cos ( b x + c ) a e a x + a b ∫ e a x sin ( b x + c ) d x = cos ( b x + c ) a e a x + a b ( a e a x sin ( b x + c ) − a b ∫ e a x cos ( b x + c ) ) d x = a 2 e a x ( a cos ( b x + c ) + b sin ( b x + c )) − a 2 b 2 I
بنابراین:
I ( 1 + b 2 a 2 ) = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 ⇒ I = e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) a 2 + b 2 . \large \begin {aligned} I \left ( 1 + \frac { b ^ 2 } { a ^ 2 } \right ) & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 } \\ \Rightarrow I & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 + b ^ 2 } . \end{aligned} I ( 1 + a 2 b 2 ) ⇒ I = a 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) = a 2 + b 2 e a x ( a cos ( b x + c ) + b sin ( b x + c ) ) .
انتگرال I = ∫ e a x sin ( b x + c ) I = \int e ^ { a x } \sin ( b x + c ) I = ∫ e a x sin ( b x + c )
حالت خاص ۳: انتگرالی به فرم ∫ a e x + b e − x p e x + q e − x d x \int \frac { a e ^ x + b e ^ { - x } } { p e ^ x + q e ^ { - x } } d x ∫ p e x + q e − x a e x + b e − x d x (NUM) = α (DEN) + β d d x (DEN) \text {(NUM)} = \alpha \text {(DEN)} + \beta \frac { d } { dx } \text {(DEN)} (NUM) = α (DEN) + β d x d (DEN) (NUM) \text {(NUM)} (NUM) (DEN) \text {(DEN)} (DEN)
مثال ۹
حاصل انتگرال نامعین زیر را به دست آورید.
∫ e x ( sin ( x ) + cos ( x ) ) d x \large \int e ^ x \big ( \sin ( x ) + \cos ( x ) \big ) \, d x ∫ e x ( sin ( x ) + cos ( x ) ) d x
حل: همانطور که میبینیم، این انتگرال به فرم ∫ e x ( f ( x ) + f ′ ( x ) ) d x \int e ^ x \big ( f ( x ) + f' ( x ) \big ) \, d x ∫ e x ( f ( x ) + f ′ ( x ) ) d x f ( x ) = sin ( x ) f(x)=\sin (x) f ( x ) = sin ( x )
e x sin ( x ) + C . \large e ^ x \sin ( x ) + C . e x sin ( x ) + C .
مثال ۱۰
انتگرال زیر را محاسبه کنید.
∫ e 2 x cos ( 5 x + 3 ) d x \large \int e ^ { 2 x } \cos ( 5 x + 3 ) \, d x ∫ e 2 x cos ( 5 x + 3 ) d x
حل: طبق رابطهای که در بالا آن را معرفی کردیم، حاصل انتگرال برابر است با:
e 2 x ( 2 cos ( 5 x + 3 ) + 5 sin ( 5 x + 3 ) ) 29 + C . \large \frac { e ^ { 2 x } \big ( 2 \cos ( 5 x + 3) + 5 \sin ( 5 x + 3 ) \big ) } {2 9 } + C . 29 e 2 x ( 2 cos ( 5 x + 3 ) + 5 sin ( 5 x + 3 ) ) + C .
مثال ۱۱
حاصل انتگرال نامعین زیر را به دست آورید.
∫ 2 e x + 3 e − x e x − 5 e − x d x \large \int \frac { 2 e ^ x + 3 e ^ { - x } } { e ^ x - 5 e ^ { -x } } \, d x ∫ e x − 5 e − x 2 e x + 3 e − x d x
حل: میتوانیم تساوی زیر را بنویسیم:
2 e x + 3 e − x = α ( e x − 5 e − x ) + β ( e x + 5 e − x ) \large 2 e ^ x + 3 e ^ { - x } = \alpha ( e ^ x - 5 e ^ { - x } ) + \beta ( e ^ x + 5 e ^ { - x } ) 2 e x + 3 e − x = α ( e x − 5 e − x ) + β ( e x + 5 e − x )
با مقایسه ضرایب e x e^x e x e − x e^{-x} e − x α + β = 2 \alpha + \beta = 2 α + β = 2 α − β = − 3 5 \alpha - \beta = - \frac{3}{5} α − β = − 5 3 α = 7 10 \alpha = \frac{7}{10} α = 10 7 β = 13 10 \beta = \frac{13}{10} β = 10 13
∫ 2 e x + 3 e − x e x − 5 e − x d x = α ∫ d x + β ∫ e x + 5 e − x e x − 5 e − x d x . ( ∗ ) \large \int \frac { 2 e ^ x + 3 e ^ { - x } } { e ^ x - 5 e ^ { - x } } d x = \alpha \int d x + \beta \int \frac { e ^ x + 5 e ^ { - x } } {e ^ x - 5 e ^ { - x } } d x . \qquad (*) ∫ e x − 5 e − x 2 e x + 3 e − x d x = α ∫ d x + β ∫ e x − 5 e − x e x + 5 e − x d x . ( ∗ )
با در نظر گرفتن e x − 5 e − x = t e ^ x - 5 e ^ {-x} = t e x − 5 e − x = t ( e x + 5 e − x ) d x = d t ( e ^ x + 5 e ^ { - x } ) d x = d t ( e x + 5 e − x ) d x = d t
( ∗ ) = 7 10 ∫ d x + 13 10 ∫ d t t = 7 x 10 + 13 10 ln ∣ t ∣ + C = 7 x 10 + 13 10 ln ∣ e x – 5 e – x ∣ + C \large \begin {aligned} ( * ) & = \frac 7 { 1 0 } \int d x + \frac { 1 3 } { 1 0 } \int \frac { d t } { t } \\ & = \frac { 7 x } { 1 0 } + \frac { 1 3 } { 1 0 } \ln | t | + C \\ & = \frac { 7 x } { 1 0 } + \frac { 1 3 } { 1 0 } \ln \big | e ^ x – 5 e ^ { – x } \big | + C \end {aligned} ( ∗ ) = 10 7 ∫ d x + 10 13 ∫ t d t = 10 7 x + 10 13 ln ∣ t ∣ + C = 10 7 x + 10 13 ln e x –5 e – x + C
که در آن، C C C
فهرست انتگرالهای نمایی
در این بخش، فهرستی از انتگرالهای توابع نمایی مختلف را ارائه میکنیم.
انتگرال نامعین
انتگرالهای نامعین، توابع پادمشتق هستند و یک عدد ثابت (ثابت انتگرالگیری) به سمت راست فرمول آنها افزوده میشود. برای سادگی، ثابت انتگرالگیری را در فرمولها نیاوردهایم.
انتگرالهایی که چندجملهای دارند
∫ x e c x d x = e c x ( c x − 1 c 2 ) \large \int x e ^ { c x } \, d x = e ^ { c x } \left ( \frac { c x - 1 }{ c ^ { 2 } } \right ) ∫ x e c x d x = e c x ( c 2 c x − 1 )
∫ x 2 e c x d x = e c x ( x 2 c − 2 x c 2 + 2 c 3 ) \large \int x ^ 2 e ^ { c x } \, d x = e ^ { c x } \left ( \frac { x ^2 } {c } - \frac { 2 x } { c ^ 2 } + \frac { 2 } { c ^ 3 } \right ) ∫ x 2 e c x d x = e c x ( c x 2 − c 2 2 x + c 3 2 )
∫ x n e c x d x = 1 c x n e c x − n c ∫ x n − 1 e c x d x = ( ∂ ∂ c ) n e c x c = e c x ∑ i = 0 n ( − 1 ) i n ! ( n − i ) ! c i + 1 x n − i = e c x ∑ i = 0 n ( − 1 ) n − i n ! i ! c n − i + 1 x i \large \begin {align} \int x ^ n e ^ { c x } \, d x & = \frac { 1 } { c } x ^ n e ^ { c x } - \frac { n } { c } \int x ^ { n - 1 } e ^ { c x } \, d x \\ & = \left ( \frac { \partial } { \partial c } \right ) ^ n \frac { e ^ { c x } } { c } \\ & = e ^ { c x } \sum _ { i = 0 } ^ n ( - 1 ) ^ i \frac { n ! }{ ( n - i ) ! c ^ { i +1 } }x ^ { n - i } \\ & = e ^ { c x } \sum _ { i = 0 } ^ n ( - 1 ) ^ { n - i } \frac { n ! } { i! c ^ { n - i + 1} } x^ i \end {align} ∫ x n e c x d x = c 1 x n e c x − c n ∫ x n − 1 e c x d x = ( ∂ c ∂ ) n c e c x = e c x i = 0 ∑ n ( − 1 ) i ( n − i )! c i + 1 n ! x n − i = e c x i = 0 ∑ n ( − 1 ) n − i i ! c n − i + 1 n ! x i
∫ e c x x d x = ln ∣ x ∣ + ∑ n = 1 ∞ ( c x ) n n ⋅ n ! \large \int \frac { e ^ { c x } } { x } \, d x = \ln | x | + \sum _ { n = 1 } ^ \infty \frac { ( c x ) ^ n } { n \cdot n ! } ∫ x e c x d x = ln ∣ x ∣ + n = 1 ∑ ∞ n ⋅ n ! ( c x ) n
∫ e c x x n d x = 1 n − 1 ( − e c x x n − 1 + c ∫ e c x x n − 1 d x ) (for n ≠ 1 ) \large \int \frac { e ^ { c x } } { x ^ n } \, d x = \frac { 1 } { n- 1 } \left ( - \frac { e ^ { c x } } {x ^ { n - 1 } } + c \int \frac { e ^{ c x } } { x ^ { n - 1} } \, d x \right ) \qquad \text{(for } n \neq 1 \text {)} ∫ x n e c x d x = n − 1 1 ( − x n − 1 e c x + c ∫ x n − 1 e c x d x ) (for n = 1 )
انتگرالهایی که فقط تابع نمایی دارند
∫ f ′ ( x ) e f ( x ) d x = e f ( x ) \large \int f' ( x ) e ^ { f ( x ) } \, d x = e ^ { f ( x ) } ∫ f ′ ( x ) e f ( x ) d x = e f ( x )
∫ e c x d x = 1 c e c x \large \int e ^ { c x } \, d x = \frac { 1 } { c } e ^ { c x } ∫ e c x d x = c 1 e c x
∫ a c x d x = 1 c ⋅ ln a a c x for a > 0 , a ≠ 1 \large \int a ^ { c x } \, d x = \frac { 1 } { c \cdot \ln a } a ^ { c x } \qquad \text{ for } a > 0 , \ a \ne 1 ∫ a c x d x = c ⋅ ln a 1 a c x for a > 0 , a = 1
انتگرالهایی که توابع نمایی و مثلثاتی دارند
∫ e c x sin b x d x = e c x c 2 + b 2 ( c sin b x − b cos b x ) = e c x c 2 + b 2 sin ( b x − ϕ ) where cos ( ϕ ) = c c 2 + b 2 \large \begin {align} \int e ^ { c x } \sin b x \, d x & = \frac { e ^ { c x } } { c^ 2 + b ^ 2 } ( c \sin b x - b \cos b x ) \\ & = \frac { e ^ { c x} } { \sqrt { c ^ 2 + b ^ 2 } } \sin ( b x -\phi ) \qquad \text {where } \cos ( \phi ) = \frac { c } { \sqrt { c ^ 2 + b ^ 2 } } \end {align} ∫ e c x sin b x d x = c 2 + b 2 e c x ( c sin b x − b cos b x ) = c 2 + b 2 e c x sin ( b x − ϕ ) where cos ( ϕ ) = c 2 + b 2 c
∫ e c x cos b x d x = e c x c 2 + b 2 ( c cos b x + b sin b x ) = e c x c 2 + b 2 cos ( b x − ϕ ) where cos ( ϕ ) = c c 2 + b 2 \large \begin {align} \int e ^ { c x } \cos b x \, d x & = \frac { e ^ { c x} } { c ^ 2 + b ^2 } ( c \cos b x + b \sin b x ) \\ & = \frac { e ^ { c x } } { \sqrt { c ^ 2+ b ^ 2 } } \cos ( b x -\phi ) \qquad \text {where } \cos ( \phi ) = \frac { c } { \sqrt { c ^ 2 + b^ 2 }} \end {align} ∫ e c x cos b x d x = c 2 + b 2 e c x ( c cos b x + b sin b x ) = c 2 + b 2 e c x cos ( b x − ϕ ) where cos ( ϕ ) = c 2 + b 2 c
∫ e c x sin n x d x = e c x sin n − 1 x c 2 + n 2 ( c sin x − n cos x ) + n ( n − 1 ) c 2 + n 2 ∫ e c x sin n − 2 x d x \large \int e ^ { c x } \sin ^ n x \, d x = \frac { e ^ { c x } \sin ^ { n - 1 } x } { c ^ 2 + n ^ 2 } ( c \sin x - n \cos x) + \frac { n ( n - 1 ) } { c ^ 2 + n ^ 2 } \int e ^ { c x } \sin ^ { n - 2 } x \, d x ∫ e c x sin n x d x = c 2 + n 2 e c x sin n − 1 x ( c sin x − n cos x ) + c 2 + n 2 n ( n − 1 ) ∫ e c x sin n − 2 x d x
∫ e c x cos n x d x = e c x cos n − 1 x c 2 + n 2 ( c cos x + n sin x ) + n ( n − 1 ) c 2 + n 2 ∫ e c x cos n − 2 x d x \large \int e ^ { c x } \cos ^ n x \, d x = \frac { e ^ { c x } \cos ^ { n - 1 } x} { c ^ 2 + n ^ 2 } ( c \cos x + n \sin x ) + \frac { n ( n - 1 ) } { c ^ 2 + n ^ 2 } \int e ^ { c x } \cos ^ { n - 2 } x \, d x ∫ e c x cos n x d x = c 2 + n 2 e c x cos n − 1 x ( c cos x + n sin x ) + c 2 + n 2 n ( n − 1 ) ∫ e c x cos n − 2 x d x
انتگرالهایی که تابع خطا دارند
در فرمولهای زیر، erf \text{erf} erf Ei \text{Ei} Ei
∫ e c x ln x d x = 1 c ( e c x ln ∣ x ∣ − Ei ( c x ) ) \large \int e ^ { c x } \ln x \, d x = \frac { 1 }{ c } \left ( e ^ { c x } \ln | x | - \operatorname { E i } ( c x ) \right ) ∫ e c x ln x d x = c 1 ( e c x ln ∣ x ∣ − Ei ( c x ) )
∫ x e c x 2 d x = 1 2 c e c x 2 \large \int x e ^ { c x ^ 2 } \, d x = \frac { 1 } { 2 c } e ^ { c x ^ 2 } ∫ x e c x 2 d x = 2 c 1 e c x 2
∫ e − c x 2 d x = π 4 c erf ( c x ) \large \int e ^ { - c x ^ 2 } \, d x = \sqrt { \frac { \pi } { 4 c } } \operatorname {erf} ( \sqrt { c } x ) ∫ e − c x 2 d x = 4 c π erf ( c x )
∫ x e − c x 2 d x = − 1 2 c e − c x 2 \large \int x e ^ { - c x ^ 2 } \, d x = - \frac { 1 } { 2 c } e ^ { - c x ^ 2 } ∫ x e − c x 2 d x = − 2 c 1 e − c x 2
∫ e − x 2 x 2 d x = − e − x 2 x − π erf ( x ) \large \int \frac { e ^ {- x^ 2 } } { x ^ 2 } \, d x = -\frac { e ^ {- x ^ 2 } } {x } - \sqrt { \pi } \operatorname {erf} ( x ) ∫ x 2 e − x 2 d x = − x e − x 2 − π erf ( x )
∫ 1 σ 2 π e − 1 2 ( x − μ σ ) 2 , d x = 1 2 erf ( x − μ σ 2 ) \large \int { \frac { 1 } { \sigma \sqrt { 2 \pi } } e ^ { -\frac { 1 } { 2 } \left ( \frac { x - \mu } { \sigma } \right ) ^ 2 }} \ , d x = \frac { 1 } {2 } \operatorname {erf} \left ( \frac { x - \mu }{ \sigma \sqrt { 2 } } \right ) ∫ σ 2 π 1 e − 2 1 ( σ x − μ ) 2 , d x = 2 1 erf ( σ 2 x − μ )
سایر انتگرالها
∫ e x 2 d x = e x 2 ( ∑ j = 0 n − 1 c 2 j 1 x 2 j + 1 ) + ( 2 n − 1 ) c 2 n − 2 ∫ e x 2 x 2 n d x valid for any n > 0 , \large \int e ^ { x ^ 2 } \, d x = e ^ { x ^ 2 } \left ( \sum _ { j = 0 } ^ { n - 1 } c _ { 2 j } \frac { 1 } { x ^ { 2 j + 1 } } \right ) + ( 2 n - 1 ) c _ { 2 n- 2 } \int \frac { e ^{ x ^ 2 } } { x ^ {2 n }} \, d x \quad \text {valid for any } n > 0 , ∫ e x 2 d x = e x 2 j = 0 ∑ n − 1 c 2 j x 2 j + 1 1 + ( 2 n − 1 ) c 2 n − 2 ∫ x 2 n e x 2 d x valid for any n > 0 ,
که در آن، c 2 j = 1 ⋅ 3 ⋅ 5 ⋯ ( 2 j − 1 ) 2 j + 1 = ( 2 j ) ! j ! 2 2 j + 1 c _ { 2 j } = \frac { 1 \cdot 3 \cdot 5 \cdots ( 2 j - 1) }{ 2 ^ { j + 1 } } = \frac { ( 2 j ) ! } {j ! 2 ^ { 2 j + 1 } } c 2 j = 2 j + 1 1 ⋅ 3 ⋅ 5 ⋯ ( 2 j − 1 ) = j ! 2 2 j + 1 ( 2 j )!
∫ x x ⋅ ⋅ x ⏟ m d x = ∑ n = 0 m ( − 1 ) n ( n + 1 ) n − 1 n ! Γ ( n + 1 , − ln x ) + ∑ n = m + 1 ∞ ( − 1 ) n a m n Γ ( n + 1 , − ln x ) (for x > 0 ) \large { \int \underbrace { x ^ { x ^ { \cdot ^ { \cdot ^ { x } } } }} _ m d x = \sum _ { n = 0 } ^ m \frac { ( - 1) ^ n ( n + 1 ) ^{ n - 1 } }{ n ! } \Gamma ( n + 1 , - \ln x ) + \sum _ { n = m + 1 } ^ \infty ( - 1) ^ n a _ { m n } \Gamma ( n + 1 , - \ln x ) \qquad \text{(for }x> 0\text{)}} ∫ m x x ⋅ ⋅ x d x = n = 0 ∑ m n ! ( − 1 ) n ( n + 1 ) n − 1 Γ ( n + 1 , − ln x ) + n = m + 1 ∑ ∞ ( − 1 ) n a mn Γ ( n + 1 , − ln x ) (for x > 0 )
که در آن،
a m n = { 1 if n = 0 , 1 n ! if m = 1 , 1 n ∑ j = 1 n j a m , n − j a m − 1 , j − 1 otherwise \large a _ { m n } = \begin {cases} 1 & \text {if } n = 0, \\ \\ \dfrac { 1 } { n ! } & \text {if } m = 1 , \\ \\ \dfrac { 1 } { n } \sum _ { j = 1 } ^ { n } j a _ { m , n -j } a _ {m - 1 , j - 1 } & \text {otherwise} \end{cases} a mn = ⎩ ⎨ ⎧ 1 n ! 1 n 1 ∑ j = 1 n j a m , n − j a m − 1 , j − 1 if n = 0 , if m = 1 , otherwise
و Γ ( x , y ) \Gamma(x,y) Γ ( x , y ) تابع گاما است.
∫ 1 a e λ x + b d x = x b − 1 b λ ln ( a e λ x + b ) \large \int \frac { 1 } { a e ^ { \lambda x } + b } \, d x = \frac { x } { b } - \frac { 1 } { b \lambda } \ln \left ( a e ^ { \lambda x } + b \right ) ∫ a e λ x + b 1 d x = b x − bλ 1 ln ( a e λ x + b )
∫ e 2 λ x a e λ x + b d x = 1 a 2 λ [ a e λ x + b − b ln ( a e λ x + b ) ] \large \int \frac { e ^ { 2 \lambda x } } { a e ^ { \lambda x } + b } \, d x = \frac { 1 } { a ^ 2 \lambda } \left [ a e ^ { \lambda x } + b - b \ln\left ( a e ^ {\lambda x} + b \right) \right] ∫ a e λ x + b e 2 λ x d x = a 2 λ 1 [ a e λ x + b − b ln ( a e λ x + b ) ]
∫ a e c x − 1 b e c x − 1 d x = ( a − b ) log ( 1 − b e c x ) b c + x . \large \int \frac { a e ^ { c x} - 1 } { b e ^ { c x } - 1 } \, d x = \frac { ( a - b ) \log ( 1 - b e^ { c x} ) } { b c} + x . ∫ b e c x − 1 a e c x − 1 d x = b c ( a − b ) log ( 1 − b e c x ) + x .
انتگرالهای معین
∫ 0 1 e x ⋅ ln a + ( 1 − x ) ⋅ ln b d x = ∫ 0 1 ( a b ) x ⋅ b d x = ∫ 0 1 a x ⋅ b 1 − x d x = a − b ln a − ln b for a > 0 , b > 0 , a ≠ b \large \begin {align} \int _ 0 ^ 1 e ^ { x \cdot \ln a + ( 1 - x ) \cdot \ln b } \, dx & = \int_0^1 \left ( \frac { a } { b } \right ) ^ { x} \cdot b\,dx \\ & = \int _ 0 ^ 1 a ^ { x} \cdot b ^ { 1 - x } \, d x \\ & = \frac { a - b } { \ln a - \ln b } \qquad\text{for } a > 0,\ b > 0,\ a \neq b \end{align} ∫ 0 1 e x ⋅ l n a + ( 1 − x ) ⋅ l n b d x = ∫ 0 1 ( b a ) x ⋅ b d x = ∫ 0 1 a x ⋅ b 1 − x d x = ln a − ln b a − b for a > 0 , b > 0 , a = b
∫ 0 ∞ e − a x d x = 1 a ( Re ( a ) > 0 ) \large \int _ 0 ^ { \infty } e ^ { - a x } \, d x = \frac { 1 } { a } \quad ( \operatorname { R e } ( a ) > 0 ) ∫ 0 ∞ e − a x d x = a 1 ( Re ( a ) > 0 )
∫ 0 ∞ e − a x 2 d x = 1 2 π a ( a > 0 ) \large \int _ 0 ^ { \infty } e ^ { - a x ^ 2 } \, d x = \frac { 1 } { 2 } \sqrt { \pi \over a } \quad (a>0) ∫ 0 ∞ e − a x 2 d x = 2 1 a π ( a > 0 )
∫ − ∞ ∞ e − a x 2 d x = π a ( a > 0 ) \large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 } \, d x = \sqrt { \pi \over a } \quad ( a > 0 ) ∫ − ∞ ∞ e − a x 2 d x = a π ( a > 0 )
∫ − ∞ ∞ e − a x 2 + b x d x = π a e b 2 4 a ( a > 0 ) \large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 + b x } \, d x = \sqrt { \pi \over a } e^ { \tfrac { b ^ 2 } { 4a } } \quad(a > 0) ∫ − ∞ ∞ e − a x 2 + b x d x = a π e 4 a b 2 ( a > 0 )
∫ − ∞ ∞ e − a x 2 e − 2 b x d x = π a e b 2 a ( a > 0 ) \large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 } e ^ { - 2b x } \, d x = \sqrt { \frac { \pi } { a } } e ^ { \frac { b ^2 } { a } } \quad ( a > 0 ) ∫ − ∞ ∞ e − a x 2 e − 2 b x d x = a π e a b 2 ( a > 0 )
∫ − ∞ ∞ x e − a ( x − b ) 2 d x = b π a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x e ^ { - a ( x - b ) ^ 2 } \, d x = b \sqrt { \frac { \pi } { a } } \quad ( \operatorname { R e } ( a ) >0 ) ∫ − ∞ ∞ x e − a ( x − b ) 2 d x = b a π ( Re ( a ) > 0 )
∫ − ∞ ∞ x e − a x 2 + b x d x = π b 2 a 3 / 2 e b 2 4 a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x e ^ { - a x ^2 + b x } \, d x = \frac { \sqrt { \pi } b } { 2 a^ { 3 / 2 } } e ^ { \frac { b ^ 2 } { 4 a } } \quad ( \operatorname { R e } ( a ) > 0 ) ∫ − ∞ ∞ x e − a x 2 + b x d x = 2 a 3/2 π b e 4 a b 2 ( Re ( a ) > 0 )
∫ − ∞ ∞ x 2 e − a x 2 d x = 1 2 π a 3 ( a > 0 ) \large \int _ { - \infty } ^ { \infty} x ^ 2 e ^ { - a x ^ 2 } \, d x = \frac { 1 } { 2 } \sqrt { \pi \over a ^ 3 } \quad ( a > 0 ) ∫ − ∞ ∞ x 2 e − a x 2 d x = 2 1 a 3 π ( a > 0 )
∫ − ∞ ∞ x 2 e − a x 2 + b x d x = π ( 2 a + b 2 ) 4 a 5 / 2 e b 2 4 a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x ^ 2 e ^ { - a x ^ 2 + b x } \, d x = \frac { \sqrt { \pi } ( 2a + b ^ 2) }{ 4 a^ { 5 / 2} } e ^ { \frac { b ^ 2 }{ 4a } } \quad ( \operatorname{Re}(a)>0) ∫ − ∞ ∞ x 2 e − a x 2 + b x d x = 4 a 5/2 π ( 2 a + b 2 ) e 4 a b 2 ( Re ( a ) > 0 )
∫ − ∞ ∞ x 3 e − a x 2 + b x d x = π ( 6 a + b 2 ) b 8 a 7 / 2 e b 2 4 a ( Re ( a ) > 0 ) \large \int _ { - \infty } ^ { \infty } x ^ 3 e ^ { - a x ^ 2 + b x } \, d x = \frac { \sqrt { \pi } ( 6 a + b ^2 ) b} { 8 a ^ {7 / 2} } e ^ { \frac { b ^ 2 } { 4a } } \quad (\operatorname{Re}(a)>0) ∫ − ∞ ∞ x 3 e − a x 2 + b x d x = 8 a 7/2 π ( 6 a + b 2 ) b e 4 a b 2 ( Re ( a ) > 0 )
∫ 0 ∞ x n e − a x 2 d x = { Γ ( n + 1 2 ) 2 ( a n + 1 2 ) ( n > − 1 , a > 0 ) ( 2 k − 1 ) ! ! 2 k + 1 a k π a ( n = 2 k , k integer , a > 0 ) (!! is the double factorial) k ! 2 ( a k + 1 ) ( n = 2 k + 1 , k integer , a > 0 ) \large \int _ 0 ^ { \infty } x ^ { n } e ^ {- a x ^ 2 } \, d x = \begin {cases} \dfrac { \Gamma \left ( \frac { n + 1 } { 2 } \right ) }{ 2 \left ( a ^ \frac { n + 1 } { 2 } \right ) } & ( n >- 1 , \ a > 0) \\ \\ \dfrac { ( 2 k - 1 ) ! ! } {2 ^ { k +1 } a ^ k } \sqrt { \dfrac { \pi } { a } } & ( n = 2 k , \ k \text { integer} , \ a > 0 ) \ \text {(!! is the double factorial)} \\ \\ \dfrac{k!}{2(a^{k+1})} & (n=2k+1,\ k \text{ integer},\ a>0) \end{cases} ∫ 0 ∞ x n e − a x 2 d x = ⎩ ⎨ ⎧ 2 ( a 2 n + 1 ) Γ ( 2 n + 1 ) 2 k + 1 a k ( 2 k − 1 )!! a π 2 ( a k + 1 ) k ! ( n > − 1 , a > 0 ) ( n = 2 k , k integer , a > 0 ) (!! is the double factorial) ( n = 2 k + 1 , k integer , a > 0 )
∫ 0 ∞ x n e − a x d x = { Γ ( n + 1 ) a n + 1 ( n > − 1 , a > 0 ) n ! a n + 1 ( n = 0 , 1 , 2 , … , a > 0 ) \large \int _ 0 ^ { \infty } x ^ n e ^ { - a x } \, d x = \begin {cases} \dfrac { \Gamma ( n + 1 )} { a ^ { n+ 1 } } & ( n > - 1 , \ a > 0 ) \\ \\ \dfrac { n ! } { a ^ { n + 1 }} & (n = 0 , 1 , 2 ,\ldots,\ a>0) \end{cases} ∫ 0 ∞ x n e − a x d x = ⎩ ⎨ ⎧ a n + 1 Γ ( n + 1 ) a n + 1 n ! ( n > − 1 , a > 0 ) ( n = 0 , 1 , 2 , … , a > 0 )
∫ 0 1 x n e − a x d x = n ! a n + 1 [ 1 − e − a ∑ i = 0 n a i i ! ] \large \int _ 0 ^ { 1 } x ^n e ^ {- a x } \, d x = \frac { n ! }{ a ^{ n + 1 } } \left[ 1 - e^ { - a } \sum _ { i = 0 } ^{ n } \frac{a^i}{i!} \right] ∫ 0 1 x n e − a x d x = a n + 1 n ! 1 − e − a i = 0 ∑ n i ! a i
∫ 0 ∞ e − a x b d x = 1 b a − 1 b Γ ( 1 b ) \large \int _ 0 ^ \infty e ^ { - a x ^ b } d x = \frac { 1 } {b } \ a ^ { - \frac { 1 } { b } } \Gamma \left ( \frac { 1 } { b } \right ) ∫ 0 ∞ e − a x b d x = b 1 a − b 1 Γ ( b 1 )
∫ 0 ∞ x n e − a x b d x = 1 b a − n + 1 b Γ ( n + 1 b ) \large \int _ 0 ^ \infty x ^ n e ^ { -ax ^ b } d x = \frac { 1 } {b } \ a ^ { - \frac { n +1 } { b} } \Gamma \left ( \frac { n +1 } { b } \right ) ∫ 0 ∞ x n e − a x b d x = b 1 a − b n + 1 Γ ( b n + 1 )
∫ 0 ∞ e − a x sin b x d x = b a 2 + b 2 ( a > 0 ) \large \int_0^{\infty} e^{-ax}\sin bx\,dx = \frac{b}{a^2+b^2} \quad (a>0) ∫ 0 ∞ e − a x sin b x d x = a 2 + b 2 b ( a > 0 )
∫ 0 ∞ e − a x cos b x d x = a a 2 + b 2 ( a > 0 ) \large \int _ 0 ^ { \infty } e ^ { - a x } \cos b x \, d x = \frac { a } {a ^ 2 + b ^2 } \quad ( a > 0 ) ∫ 0 ∞ e − a x cos b x d x = a 2 + b 2 a ( a > 0 )
∫ 0 ∞ x e − a x sin b x d x = 2 a b ( a 2 + b 2 ) 2 ( a > 0 ) \large \int _ 0 ^ { \infty } x e ^ { - a x } \sin b x \, d x = \frac { 2 ab } { ( a ^ 2 + b ^2 ) ^ 2} \quad ( a > 0 ) ∫ 0 ∞ x e − a x sin b x d x = ( a 2 + b 2 ) 2 2 ab ( a > 0 )
∫ 0 ∞ x e − a x cos b x d x = a 2 − b 2 ( a 2 + b 2 ) 2 ( a > 0 ) \large \int _ 0 ^ { \infty } x e ^ { - a x } \cos b x \, d x = \frac { a ^2 - b ^ 2 }{ ( a^ 2 + b ^ 2 ) ^ 2 } \quad (a>0) ∫ 0 ∞ x e − a x cos b x d x = ( a 2 + b 2 ) 2 a 2 − b 2 ( a > 0 )
∫ 0 2 π e x cos θ d θ = 2 π I 0 ( x ) \large \int _ 0 ^ { 2 \pi } e ^ { x \cos \theta } d \theta = 2 \pi I_0(x) ∫ 0 2 π e x c o s θ d θ = 2 π I 0 ( x )
∫ 0 2 π e x cos θ + y sin θ d θ = 2 π I 0 ( x 2 + y 2 ) \large \int _ 0 ^ { 2 \pi } e ^ { x \cos \theta + y \sin \theta} d \theta = 2 \pi I _ 0 \left( \sqrt{x^2 + y^2} \right) ∫ 0 2 π e x c o s θ + y s i n θ d θ = 2 π I 0 ( x 2 + y 2 )
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش انتگرال توابع نمایی – از صفر تا صد فیلم آموزشی انتگرال توابع نمایی فیلم آموزشی حل چند مثال از انتگرال توابع نمایی فیلم آموزشی انتگرال با لگاریتم طبیعی فیلم آموزشی حل چند مثال از انتگرال با لگاریتم طبیعی فیلم آموزشی انتگرال با قضیه جز به جز فیلم آموزشی حل مثال از انتگرال با قضیه جز به جز فیلم آموزشی انتگرال ضرب توابع نمایی و مثلثاتی 
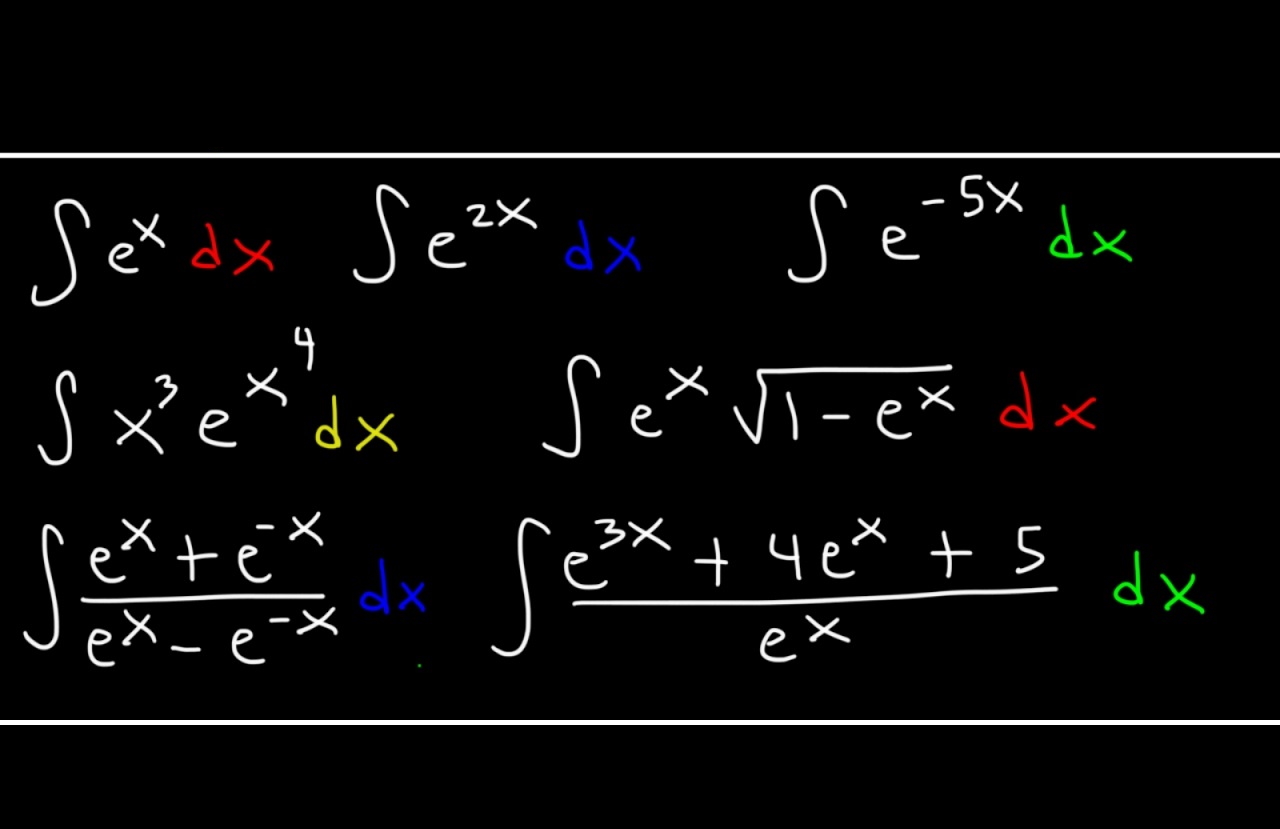
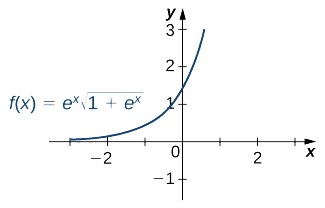













با سلام و وقت بخیر
انتگرال تابع نمایی مختلط به چه صورت؟