چگالی طیف توان سیگنال چیست؟ – از صفر تا صد
«طیف توان» (Power Spectrum) یا «چگالی طیف توان» (Power Spectral Density) یک سیگنال در واقع به این سوال پاسخ میدهد که «چه مقدار از توان یک سیگنال در فرکانس قرار گرفته است؟» پاسخ به این سوال در قالب توزیع مقادیر توان به عنوان تابعی از فرکانس است. میدانیم که توان برابر با میانگین مربعات سیگنال در نظر گرفته میشود. در حوزه فرکانس این مقدار برابر با مربع دامنه مقادیر تبدیل فوریه سریع یا FFT سیگنال است. در این مطلب قصد داریم به تعریف طیف توان یا چگالی طیف توان یک سیگنال و نحوه محاسبه آن بپردازیم.
طیف توان یک سیگنال را میتوان به صورت یک باره و برای تمام سیگنال محاسبه کرد که در این صورت به آن «دوره نگار» یا «پریودگرام» (Periodogram) میگویند. همچنین میتوان از دوره نگار بخشهای مختلف سیگنال زمانی با یکدیگر میانگین گرفت و به این ترتیب چگالی طیف توان را به دست آورد.
میدانیم که سیگنالهای متناوب در یک مولفه اساسی و هارمونیکهای آن پیک میزنند. همچنین پیک سیگنالهای «شبه پریودیک» (Quasiperiodic) در ترکیبات خطی از دو یا چند فرکانس وابسته قرار دارد. «دینامیکهای آشوبناک» (Chaotic Dynamics) مولفههای باند گستردهای به طیف میدهند. در حقیقت این ویژگی بعدا به عنوان یک معیار برای شناسایی یک دینامیک به عنوان آشوب مورد استفاده قرار میگیرد. تمام این موارد بر اساس طیف توان سیگنال بیان میشود.
یک طیف توان زمانی ایدهآل در نظر گرفته میشود که دنبالهای بینهایت از دادههای پیوسته درباره سیگنال در دست باشند. در حالی که در عمل همواره برای فرکانس نمونه برداری و نیز طول دادهها محدودیت وجود دارد و به عبارت دیگر، دادههای با طول محدود در اختیار ما قرار دارد. در نتیجه بسیار مهم است که مشخص شود این موارد چگونه بر طیف توان یک سیگنال اثر خواهند گذاشت.
طیف توان سیگنال گسسته در زمان
فرض میکنیم هیچ نگرانی درباره طول دادهها نداشته باشیم یا به عبارت دیگر، یک دنباله زمانی پیوسته با طول نامحدود در اختیار داشته باشیم. در این صورت:
طیف توان این سیگنال یا با استفاده از رابطه زیر محاسبه میشود:
که تبدیل فوریه سیگنال است و به صورت زیر به دست میآید:
از طرف دیگر، ما همواره با سیگنال رو به رو هستیم که در طول بازه محدود با نرخ نمونه برداری محدود اندازهگیری شده است. بنابراین ما N نمونه از سیگنال Y را داریم که در بازه اندازهگیری شده است. همچنین رابطه صادق است. بنابراین برای تخمین طیف توان یک سیگنال میتوانیم سری فوریه سیگنال را محاسبه کنیم:
در عبارت فوق، فرکانسهای گسسته و زمانهای گسسته برابر با و هستند. البته برای یک سیستم گسسته با زمان، دینامیکها به صورت عباراتی با اندیس j نوشته میشوند. در ادامه N را به صورت یک عدد زوج در نظر میگیریم. در نتیجه تخمین طیف توان به صورت زیر محاسبه خواهد شد:
در این رابطه، از به دلیل حقیقی بودن سیگنال و بنا بر روابط قبل استفاده میکنیم. از P فقط برای فرکانسهای مثبت استفاده میکنیم. در تصویر زیر طیف توان برای سیگنال با و نشان داده شده است.
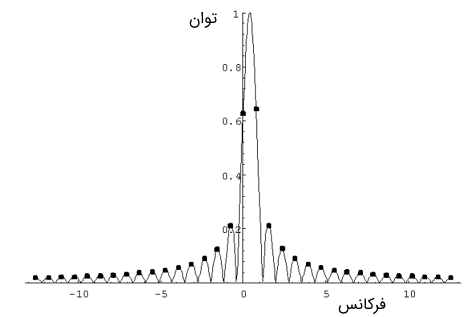 " width="468" height="317">
" width="468" height="317">پریودگرام سیگنال
همان طور که قبلا اشاره کردیم، پریودگرام، طیف توان را برای تمام سیگنال ورودی محاسبه میکند. برای محاسبه پریودگرام یک سیگنال از رابطه زیر استفاده میکنیم:
در رابطه بالا، نشان دهنده تبدیل فوریه سیگنال ورودی و N برابر با فاکتور نرمال کننده است که در عملکرد پریودگرام برابر با تعداد نمونههای سیگنال فرض میشود. عملکرد پریودگرام را میتوان توسط «پنجره طیفی» (Spectral Windowing) ارتقا داد.
مقدار به دست آمده برای یک پریودگرام را میتوان در یک فاکتور ضرب کرد تا بتوان قضیه پارسوال را اعمال کرد. نتیجه به صورت زیر خواهد بود:
در رابطه فوق فرض میشود که با استفاده از دادههای سیگنال حوزه زمان، سیگنال FFT حوزه فرکانس دو طرفه محاسبه شده است و N برابر با تعداد نمونههای سیگنال حوزه زمان است. البته به این نکته توجه کنید که نرمالیزه کردن نتایج یک پریودگرام به عواملی مانند این که پریودگرام یک طرفه یا دو طرفه باشد و نیز توان متوسط هر تابع پنجره طیفی بستگی دارد. بنابراین میتوان نرمالیزه کردن را به نحوی متفاوت انتخاب کرد.
هنگامی که تابع پنجره به یک سیگنال اعمال میشود، مقدار توان موجود در سیگنال کاسته میشود. به همین دلیل باید از یک ضرب جبران کننده برابر با برای جبران مقدار توان تضعیف شده استفاده کرد. برای یک «پنجره هنینگ» (Hanning Window) این مقدار به صورت تئوری برابر با ۰٫۳۷۵ است. پس به دلیل این که فاکتور نرمالیزه کننده در مخرج قرار دارد، باید N را بر ۰٫۳۷۵ تقسیم کنید تا جبران سازی برای پنجره هنینگ صورت گیرد.
چگالی طیف توان سیگنال
چگالی طیف توان یا PSD یک نمودار در حوزه فرکانس به شمار میآید که توان سیگنال را بر حسب مقادیر مختلف فرکانس آن ترسیم میکند. میانگین گرفتن از پریودگرامهای بخشهای (Segment) مختلف سیگنالهای طولانی به صورت بسیار دقیقتری توان را به فرکانسهای صحیح اختصاص میدهد و نیز باعث کاهش نوسانات شامل نویز در دامنه توان میشود. البته در عوض رزولوشن فرکانسی کاهش مییابد؛ زیرا در این حالت تعداد نقاط داده بسیار کمتری برای محاسبه هر FFT در اختیار ما قرار دارد.
دقت محاسبه چگالی طیف توان یا PSD را نیز میتوان از طریق «پنجره طیفی» (Spectral Windowing) بهبود داد که هر بخش یا سگمنت یک پنجره در نظر گرفته میشود. اما با استفاده از روش پنجره همکاری و تاثیر سیگنال نزدیک به انتهای هر بخش حذف میشود. برای غلبه بر این مشکل باید سگمنتها با یکدیگر همپوشانی داشته باشند. در تصویر زیر نمایی از یک سیگنال حوزه زمان همراه با سه تابع پنجره برای هر سگمنت نشان داده شده است.

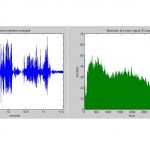
همچنین در تصویر زیر مثالی از میانگینگیری از ۸ پریودگرام برای سگمنتهای هم پوشان مربوط به یک سیگنال صوتی نمونه برداری شده نشان داده شده است.
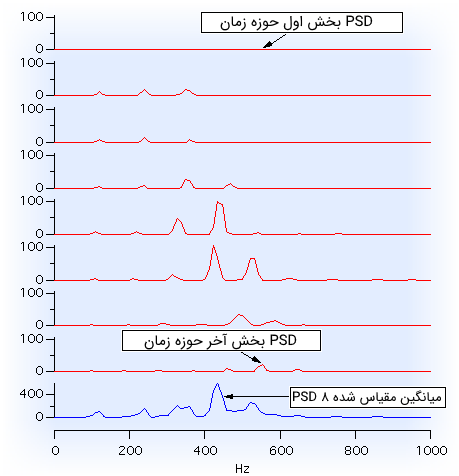
چگالی طیف توان یک سیگنال تصادفی
بسیاری از سیگنالهایی که در کاربردهای عملی با آن ها مواجه هستیم به صورتی هستند که تغییرات آنها در طول زمان را نمیتوان به صورت دقیق توصیف کرد. در مورد این سیگنالها فقط میتوان عباراتی احتمالاتی برای توصیف تغییرات به کار برد. ابزار ریاضی برای مطالعه این سیگنالها، همان ابزاری است که برای توصیف «دنبالههای تصادفی» (Random Sequence) مورد استفاده قرار میگیرد که متشکل از گروهی از «تحققهای» (Realizations) محتمل است که هر کدام دارای احتمال وقوع مختص به خود هستند. واضح است که از کل گروه تحقق، هر «آزمایش کننده» (Experimenter) فقط یکی از تحققهای سیگنال را مشاهده (Observe) میکند.
ممکن است به این صورت تصور شود که میتوان یک تعریف «قطعی» (Deterministic) را برای توصیف این سیگنالها نیز مورد استفاده قرار داد. اما این تصور غلط است؛ زیرا تحقق یک سیگنال تصادفی به صورت یک دنباله گسسته با زمان دیده میشود که انرژی محدود ندارد و به همین دلیل نمیتوان از تبدیل فوریه گسسته با زمان یا DTFT در مورد آنها استفاده کرد. یک سیگنال تصادفی همواره دارای توان متوسط محدود است و بنابراین میتوان با یک چگالی طیف توان میانگین آنها را توصیف کرد. برای سادگی در ادامه به این مقدار فقط با نام چگالی طیف توان اشاره خواهیم کرد.
سیگنال گسسته با زمان را در نظر بگیرید و فرض کنید که یک دنباله از متغیرهای تصادفی با میانگین صفر باشند:
در رابطه فوق، اپراتور «امید ریاضی» (Expectation) است که در طول نمونههای تحقق، میانگین میگیرد. خودهمبستگی (Autocovariance) یا تابع کواریانس به صورت زیر تعریف میشود:
فرض میشود که این مقدار فقط به تاخیر بین دو نمونه میانگینگیری شده بستگی داشته باشد. حال با توجه به دو رابطه فوق، میتوان به این نتیجه رسید که سیگنال یک دنباله ایستای مرتبه دو است. هنگامی که بخواهیم دنباله خود همبستگی چند سیگنال مختلف را از یکدیگر تفکیک کنیم، از یک اندیس پایین برای نشان دادن سیگنال متناظر با آن استفاده میکنیم (مثلا ).
دنباله خود همبستگی دارای چندین ویژگی بسیار ساده، اما مهم است. ویژگی اول عبارت است از:
این معادله را با استفاده از فرمولهای فوق و ویژگی ایستا بودن سیگنال به دست آورده ایم. ویژگی دوم را نیز میتوان به صورت زیر نوشت:
ویژگی دوم با توجه به این واقعیت به دست آمده است که ماتریس کواریانس به صورت زیر تعریف میشود:
که برای تمام مقادیر m «مثبت معین» (Positive Semidefinite) است. میدانیم که یک ماتریس هرمیتی M مثبت معین است، اگر برای هر بردار a داشته باشیم . چون رابطه زیر صحیح است:
که در این رابطه داریم:
بنابراین دیدیم که برای هر m مثبت معین است. در نتیجه خاصیت دوم خودهمبستگی با استفاده از این روابط به دست آمده است. در تصویر زیر نمایی از تابع خود همبستگی و چگالی طیف توان یک سیگنال نشان داده شده است.
برای چگالی طیف توان یک سیگنال تصادفی دو تعریف وجود دارد که در ادامه به بررسی آن ها میپردازیم.
تعریف اول چگالی طیف توان سیگنال تصادفی
چگالی طیف توان یک سیگنال تصادفی را در یک تعریف میتوان به صورت تبدیل فوریه گسسته با زمان دنباله خودهمبستگی سیگنال در نظر گرفت:
تبدیل معکوس که را مجددا به دست میآورد، به صورت زیر است:
در نتیجه میتوان نوشت:
پس صحیح بودن رابطه معکوس اثبات میشود. رابطه زیر صحیح است:
حال چون است، در نتیجه با استفاده از رابطه فوق، مقدار توان متوسط را اندازهگیری میکند و بنا بر آن چه گفتیم، میتوان آن را چگالی طیفی توان سیگنال تصادفی نام نهاد؛ زیرا این تابع توزیع مقادیر توان متوسط سیگنال را در طول فرکانسهای مختلف نشان میدهد. همچنین میتوان گفت که با توجه به رابطه فوق، تخمین توان محدود در باند فرکانسی تا است و توان کلی سیگنال را میتوان با استفاده از انتگرالگیری از این توان محدود به دست آورد.
تعریف دوم چگالی طیف توان سیگنال تصادفی
تعریف دوم برای محاسبه چگالی طیف توان به صورت زیر است:
بنابراین میتوان ثابت کرد که تعریف دوم برای چگالی طیفی توان با تعریف اول برای چگالی طیف توان یکسان است.
به طریق زیر:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی برق
- آموزش تجزیه و تحلیل سیگنال ها و سیستم ها
- پهنای باند معادل نویز (ENBW) چیست؟ — از صفر تا صد
- مدولاسیون کد پالس (PCM) چیست؟ — از صفر تا صد
- حلقه قفل فاز (PLL) چیست؟ — از صفر تا صد
^^