مدار معادل موتور القایی — به زبان ساده
در آموزشهای پیشین مجله فرادرس، با موتورهای الکتریکی و کنترل آنها آشنا شدیم. همانطور که میدانیم، موتورهای القایی کاربردهای صنعتی و خانگی فراوانی دارند. در این موتورها، با تغییر میدان مغناطیسی سیمپیچی استاتور، یک جریان الکتریکی در روتور القا میشود. این جریان، میدان مغناطیسی مربوط به خود را تولید میکند که با میدان استاتور برای ایجاد گشتاور و چرخش تعامل دارد. تحلیل موتور القایی با استفاده از مدار معادل آن کار آسانتری است. در این آموزش، مدار معادل موتور القایی را ارائه خواهیم کرد.
لغزش و فرکانس در موتور القایی
قبل از بحث درباره مدار معادل موتور القایی چند اصطلاح و کمیت مربوط به آن بررسی میکنیم.
لغزش
همانطور که میدانیم، موتورهای القایی آسنکرون هستند؛ بدین معنی که میدان مغناطیسی استاتور در سرعت سنکرون موتور ($$n_s$$) میچرخد و روتور هیچگاه در سرعت سنکرون نمیچرخد، در غیر این صورت جریانی القا نخواهد شد. اختلاف بین سرعت سنکرون موتور و سرعت آسنکرون آن «لغزش» (Slip) نامیده میشود. لغزش بار کامل معمولاً از کمتر از ۱ درصد برای موتورهای بزرگ (با توان بالا) تا ۶ درصد برای موتورهای کوچک (با توان پایین) است.
همانطور که گفتیم، اختلاف بین سرعت سنکرون ($$n_s$$) و سرعت واقعی روتور ($$n_r$$)، لغزش ($$s$$) است. به عبارت دیگر، لغزش را به شکل کسر زیر مینویسیم:
$$ \large s = \frac { n _ s - n _ r } { n _ s } $$
فرکانس
با توجه به نظریه میدانهای مغناطیسی، رابطه بین فرکانس جریان استاتور ($$f$$)، تعداد جفتقطبها ($$p$$) و سرعت سنکرون به صورت زیر است:
$$ \large f = n _ s p $$
فرکانس جریان در روتور ($$f _ r $$) برابر با اختلاف سرعت روتور و استاتور ضرب در تعداد جفتقطبها به صورت زیر است:
$$ \large f _ r = ( n _ s - n _ r ) p $$
با ترکیب معادله اخیر و لغزش، داریم:
$$ \large f _ r = s n _ s p = s f $$
سرعت سنکرون برحسب دور در ثانیه نیز برابر است با:
$$ \large n _ s = \frac {f } { p } $$
این مقدر برحسب دور در دقیقه (rpm) به صورت زیر در میآید:
$$ \large n _ s = \frac{ 60 f } {p}$$
کمیت $$n_s$$ سرعتی است که شار مغناطیسی نسبت به استاتور میچرخد و $$ s n _s $$ سرعت شار روتور نسبت به روتور است. البته، خود روتور با سرعت $$ n _ r $$ میچرخد و سرعت کلی شار روتور برابر خواهد بود با:
$$ \large s n _ s + n _r = ( n _ s - n _ r ) + n _ r = n _ s $$
همانطور که میبینیم سرعت چرخش شار استاتور و شار روتور برابر است. در نتیجه میتوان موتور القایی را مشابه ترانسفورماتور با یک فاصله هوایی تحلیل کرد.
مدار معادل موتور القایی
همانطور که گفتیم، میتوانیم از مدار معادل ترانسفورماتور برای تشکیل مدار معادل موتور القایی استفاده کنیم. مدار معادل موتور القایی به صورت زیر است.
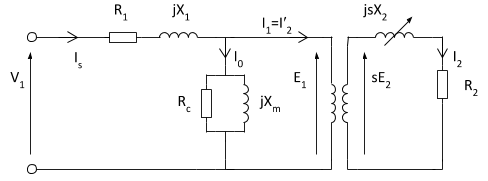
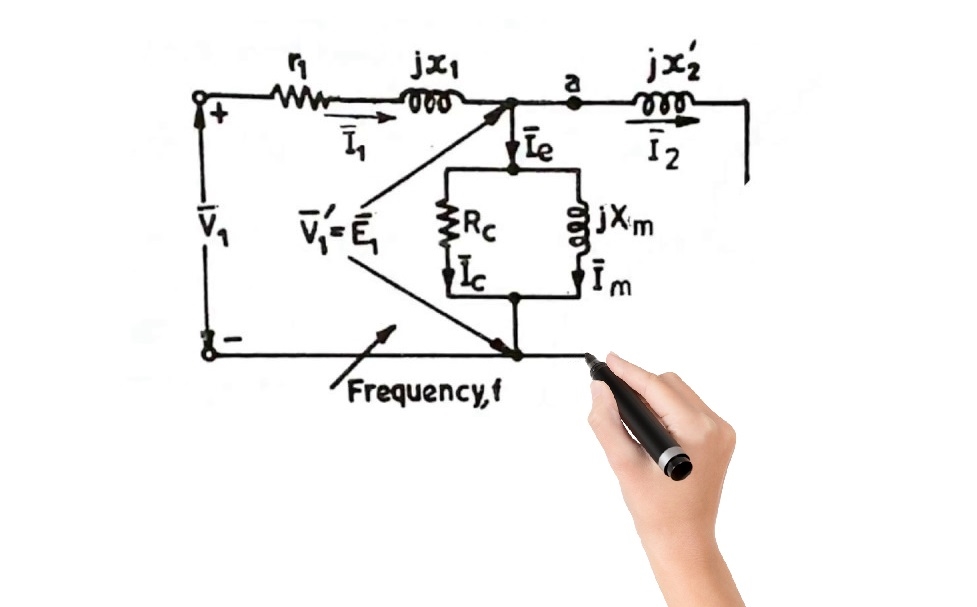
در مدار شکل بالا، $$R_1$$ مقاومت سیمپیچی استاتور است و $$ X _ 1$$ راکتانس نشتی (شاری که با فاصله هوایی و روتور پیوند ندارد) را نشان میدهد. راکتانس مغناطیسی فاصله هوایی $$X _ m $$ و تلفات هسته (هیسترزیس و جریان فوکو) نیز با $$ R _ c $$ نشان داده شدهاند.
یک ترانسفورماتور ایدهآل با تعداد دورهای اولیه $$N_1$$ و ثانویه $$ N _ 2 $$ نیز نشان دهنده فاصله هوایی هستند. در سمت روتور، نیروی محرکه الکتریکی (emf) تحت تأثیر لغزش قرار میگیرد (وقتی سرعت روتور زیاد شود، لغزش کاهش یافته و در نتیجه، emf کمتری القا میشود). مقاومت و راکتانس روتور نیز به ترتیب با $$ R _ 2 $$ و $$ X _ 2 $$ مشخص شدهاند. راکتانس $$ X _ 2$$ وابسته به فرکانس نیروی محرکه الکتریکی سلف روتور است. جریان $$I_2 $$ مدار روتور برابر است با:
$$ \large I _ 2 = \frac { s E _ 2 } { \sqrt {( R _ 2 ) ^ 2 + (s X _ 2 ) ^ 2 } } $$
یا
$$ \large I _ 2 = \frac { E _ 2 } { \sqrt {( \frac {R _ 2 } { s} ) ^ 2 + ( X _ 2 ) ^ 2 } } $$
با توجه به معادله اخیر، میتوانیم مدار معادل شکل ۱ را به صورت زیر رسم کنیم.
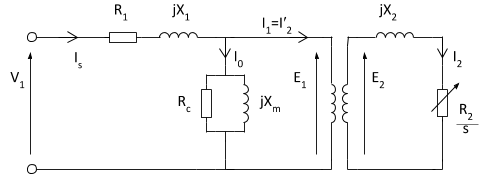
در ادامه، مدار معادل را سادهتر خواهیم کرد.
مدار معادل ساده شده
در مدار معادل شکل ۲، وابستگی محاسبه ولتاژ و فرکانس ثانویه به لغزش حذف شده است. در نتیجه، میتوانیم با حذف ترانسفوماتور ایدهآل و ارجاع مقاومت و راکتانس روتور به سمت اولیه (که با علامت پریم (') مشخص شده است)، ترانسفورماتور را حذف کرده و به مدار معادل ساده شده شکل ۳ برسیم.
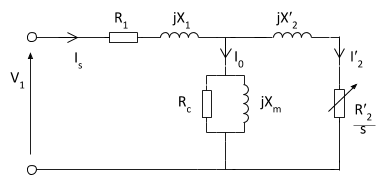
مقادیر ارجاع داده شده جدید با ضرب $$ k ^ 2 $$ در مقادیر قبلی به دست آمدهاند. پارامتر $$k$$ نسبت تعداد دورهای مؤثر سیمپیچ استاتور به روتور است.
لازم به ذکر است که به دست آوردن پارامترهای مدار معادل از طریق آزمونهای dc، بیباری، و روتور قفل شده به سادگی انجام میشود.
محاسبات مربوط به عملکرد موتور
با داشتن مدار معادل ساده شده میتوانیم محاسبات مربوط به عملکرد یک موتور القایی را انجام دهیم. توجه کنید که محاسبات پارامترها به صورت برداری است و برای آنکه جابهجایی فاز، ضریب توان و... از محاسبات حذف شود، باید از نمایش مختلط یا فازوری استفاده کنیم.
جریان موتور
وقتی پارامترهای مدار معادل موتور را به دست آوردیم، میتوانیم با ساده کردن مدار معادل به امپدانس $$ Z _ { e q } $$ (یا استفاده از امپدانس تونن معادل) به سادگی جریان موتور را به دست آوریم:
$$ \large I _ s = \frac { V _ 1 } { Z _ {eq}} $$
با توجه به مدار معادل، $$ Z _ { eq } $$ برابر است با:
$$ \large Z _ { e q } = R _ {e q } + \frac { R' _ 2 } { s } +j X _ { e q } $$
از این معادله میتوان دریافت که با افزایش سرعت روتور (کاهش لغزش)، امپدانس مدار افزایش و جریان استاتور کاهش پیدا میکند.
توان موتور
اگر، برای سادهسازی، از تلفات هسته ($$R_c$$) چشمپوشی کنیم، خواهیم داشت: $$ I _ s = I'_2$$. در این حالت، توانی که به موتور تحویل داده میشود ($$ P _ {in}$$)، در هر فاز برابر است با:
$$ \large P _ { i n } = I _ s ^ 2 \left ( R _ 1 + \frac {R' _ 2 } { s } \right ) $$
توان تلف شده در سیمپیچها نیز به صورت زیر به دست میآید:
$$ \large P _ w = I _ s ^ 2 ( R _ 1 + R' _ 2 ) $$
اختلاف بین توانی که موتور را تغذیه میکند و توان تلف شده در سیمپیچها، برابر با توانی است که به بار منتقل میگردد ($$P _ m $$). این توان در هر فاز برابر است با:
$$ \large P _ m = P _ { in } - P _ { w } = I _ s ^ 2 \left ( \frac {1 - s } { s } \right ) R' _ 2 $$
و برای هر سه فاز داریم:
$$ \large P _ { m 3 \phi } = 3 \times I _ s ^ 2 \left ( \frac {1 - s } { s } \right ) R' _ 2 $$
گشتاور موتور
با دانستن این نکته که توان موتور برابر با ضرب گشتاور موتور ($$M$$) در سرعت زاویهای ($$\omega$$) است، میتوانیم گشتاور ($$T$$) را به صورت زیر فرمولبندی کنیم:
$$ \large T = \frac { P _ { m 3 \phi }}{ \omega } $$
و
$$ \large \omega = \frac { 2 \pi n _ r } { 60 } = \frac { 2 \pi } { 60 } ( 1 - s ) n _ s $$
با ترکیب فرمول توان موتور در معادله گشتاور، داریم:
$$ \large T = \frac { 3 \times I _ s ^ 2 \left ( \frac {1-s } { s } \right ) R' _ 2 } { \frac { 2 \pi } { 60 } ( 1 - s ) n _ s } = I _ s ^ 2 \frac {90 } {\pi} \frac {R' _ 2 } { s } $$
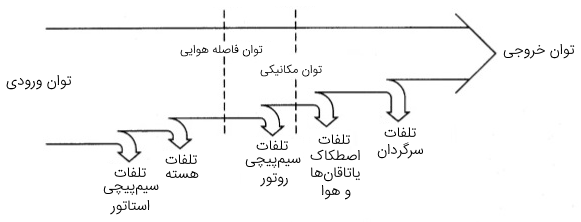
نمودار پخش توان
در بخشهای قبلی درباره نحوه محاسبه پارامترهای مختلف موتور با استفاده از مدار معادل ساده شده و نیز چشمپوشی از تلفات آهن هسته بحث کردیم. برای دقت بیشتر در محاسبات، میتوانیم تلفات آهن هسته را نیز در نظر بگیریم.
با توجه به مواردی که گفته شد، نمودار پخش توان موتور القایی مطابق شکل ۴ است.
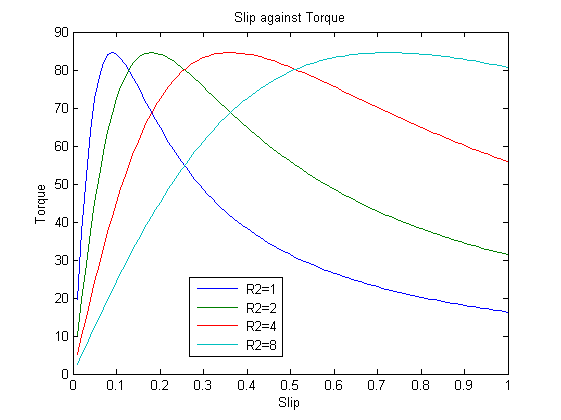
مثال
یک موتور سهفاز 400 ولت با ۴ جفت قطب را در نظر بگیرید که پارامترهای مدار معادل آن به صورت زیر هستند:
$$ \large R _ 1 = 1 \, \Omega, \; \; \; \; X _ 1 = 3 \, \Omega, \; \; \; \; X'_2 = 2 \Omega $$
مشخصه گشتاور-لغزش را برای مقادیر مقاومتهای ۱، ۲، ۴ و ۸ اهم $$ R'_2$$ رسم کنید.
حل: برای ساده کردن تحلیل، از جریان مغناطیسشوندگی و تلفات آهنی هسته صرفنظر میکنیم (یعنی $$ R _ c = iX _ m = 0 $$). با توجه به مدار معادل ساده شده، اندازه جریان $$I_s$$ استاتور برابر است با:
$$ \large | I _ s | = \frac { | V _ 1 | } {\sqrt { \left [ \left ( R _ 1 + \frac {R' _ 2} { s} \right ) ^ 2 + ( X _ 1 + X' _ 2 ) ^ 2 \right ]}} $$
و با جایگذاری آن در معادله گشتاور، داریم:
$$ \large T = \frac { 90 } { \pi n _ s } \frac { R' _ 2 } { s } \frac { | V _ 1 | ^ 2 } { \left [ \left ( R _ 1 + \frac {R' _ 2} { s} \right ) ^ 2 + ( X _ 1 + X' _ 2 ) ^ 2 \right ]} $$
برنامه متلب نمودار گشتاور-لغزش با استفاده از معادله اخیر به صورت زیر است:
1V1 = 400/sqrt(3); % phase voltage (V)
2R1 = 1; % stator winding resistance (?)
3X1 = 3; % stator reactance (?)
4X2 = 8; % rotor reactance (?)
5
6p=4; % number of pole pairs
7f=50; % frequency, Hz
8ns=60*f/p; % synchronouse seed (rev.s-1)
9
10s = 0:0.01:1; % slip values
11torque=[]; curve={};
12
13for R2 = [1 2 4 8] % rotor winding resistance
14 k = ((90*R2*V1^2)./(pi*ns*s));
15 d = (R1+R2./s).^2+(X1+X2)^2;
16 torque(:,end+1) = k./d;
17 curve{end+1} = strcat(' R2=', num2str(R2));
18end
19plot(s,torque);title('Slip against Torque');
20xlabel('Slip'); ylabel('Torque'); legend(curve,0)نمودارهای حاصل از اجرای برنامه فوق نیز مطابق شکل ۴ خواهند بود.
نمادهای مدار معادل موتور القایی
نمادهای به کار رفته در مدار معادل موتور القایی به شرح زیر است:
- $$f$$: فرکانس مدار استاتور (هرتز)
- $$f_ r $$: فرکانس مدار روتور (هرتز)
- $$ I _ 1 $$ و $$ I _ s $$: جریان استاتور (آمپر)
- $$ I _ 2 $$: جریان روتور (آمپر)
- $$ K $$: نسبت دور مؤثر سیمپیچهای استاور به روتور
- $$N _ 1 $$: تعداد دورهای اولیه ترانسفورماتور ایدهآل مدار معادل
- $$N _ 2 $$: تعداد دورهای ثانویه ترانسفورماتور ایدهآل مدار معادل
- $$ n _ r $$: سرعت روتور (rpm یا دور بر دقیقه)
- $$ n _ s $$: سرعت سنکرون (rpm یا دور بر دقیقه)
- $$ p $$: تعداد جفت قطبها
- $$ P _ c $$: تلفات آهن (هسته) موتور (وات)
- $$ P _ {in} $$: توان ورودی موتور (وات)
- $$ P _ m$$: توان تحویلی به بار (وات)
- $$P _ w $$: تلفات توان سیمپیچی (استاتور+روتور) (وات)
- $$ R _ 1 $$: مقاومت مدار روتور (اهم)
- $$ R _ 2 $$: مقاومت مدار استاتور (اهم)
- $$ s$$: لغزش
- $$T$$: گشتاور موتور (نیوتن در متر)
- $$ \omega $$: سرعت زاویهای روتور (رادیان بر ثانیه)
- $$ X _ 1 $$: راکتانس نشتی استاتور (اهم)
- $$ X _ 2 $$: راکتانس مدار روتور (اهم)
- $$ X _ m $$: راکتانس مغناطیس شوندگی (اهم)
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- آشنایی با ترانسفورماتورها — مجموعه مقالات جامع وبلاگ فرادرس
- منبع تغذیه سوئیچینگ — به زبان ساده
- ال ای دی (LED) چیست؟ — به زبان ساده
^^











درود و تشکر از شما ،گشتاور در حالت ستاره 1/3مثلث هست؟
ممنون مهندس عالی بود ،مهندس برای رسم مشخصه گشتاور لغزش که با متلب رسم کردید ،اگه بخواهیم از همون روش تحلیلی هندسی استفاده کنیم امکانش هست؟(یعنی اینکه برای مثال چون معادله ما سهمی هست حدودا شکل ما این میشه یا …)،من ریاضیم ضعیفه
باسلام وبا تشکر از مطالب مفید شما در مورد موتور های القایی ،استنباطم این است که در زیر تیتر لغزش ودر این جمله ((معمولا سرعت روتور 2ت6 درصد سرعت سنکرون است))کلمه ای جاافتاده است.
ولی این مسِآله ازوزین بودن و ارایه عالی شما چیزی کم نمیکند.
با تشکرفراوان
سلام.
منظور از جمله مذکور، درصد اختلاف سرعت روتور و سرعت سنکرون نسبت به سرعت سنکرون بوده است که اصلاح شد.
از اینکه با مجله فرادرس همراه هستید، خوشحالیم و سپاسگزاریم که با ارائه بازخوردهای دقیق ما را در افزایش کیفیت مطالب کمک میکنید.