عملگر دیفرانسیلی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

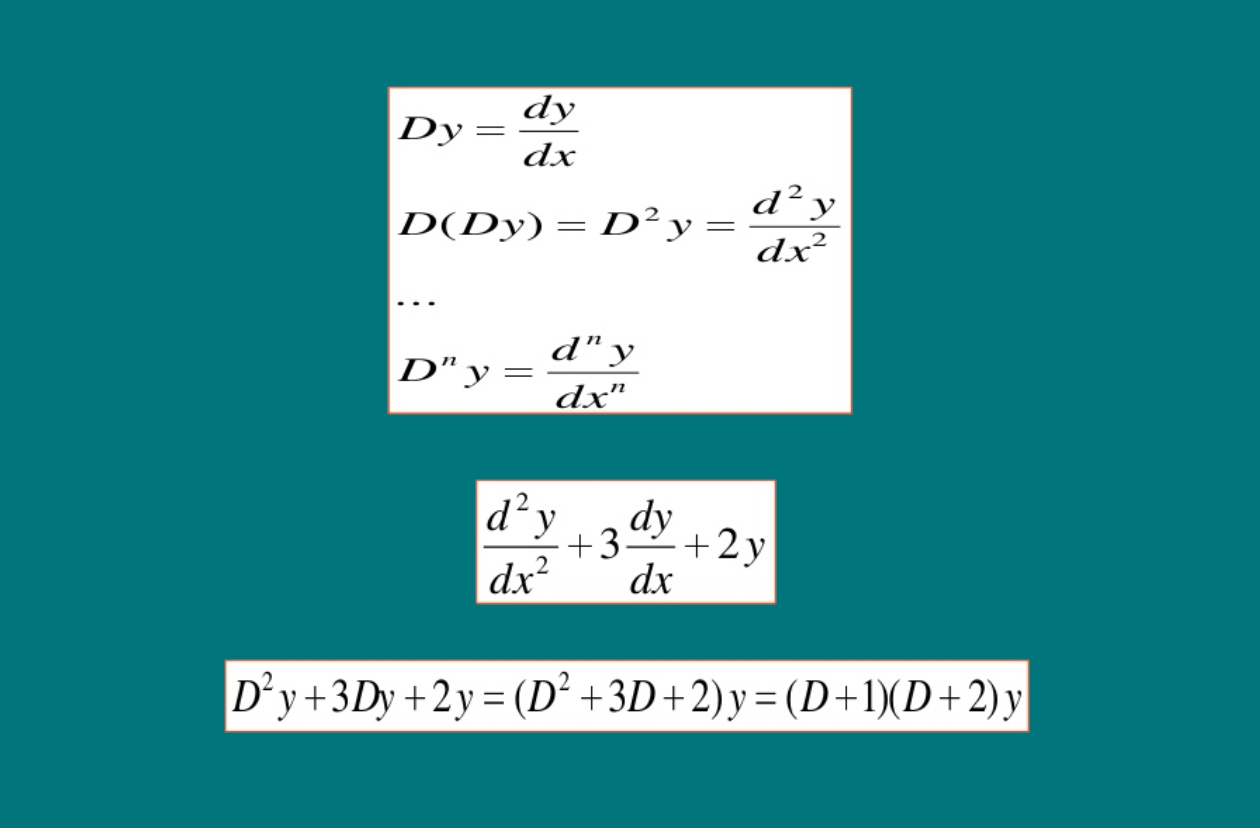
در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین به روش حل معادلات خاص، مانند معادله لاگرانژ و معادله کلرو پرداختیم. در این آموزش، یکی از ابزارهای حل معادلات دیفرانسیل،‌ یعنی «عملگر دیفرانسیلی» (Differential Operator) را معرفی می‌کنیم.

تعریف عملگر دیفرانسیلی

عملگرها یا اپراتورهای دیفرانسیلی، تعمیمی از عملیات مشتق‌گیری هستند. ساده‌ترین عملگر دیفرانسیلی $$D$$ روی تابع $$y$$ عمل کرده و مشتق اول آن را نتیجه می‌دهد:

$$ \large D y \left ( x \right ) = y ’ \left ( x \right ) . $$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

دو بار اعمال $$D$$ منجر به مشتق دوم $$y(x)$$ می‌شود:

$$ \large { { D ^ 2 } y \left ( x \right ) = D \left ( { D y \left ( x \right ) } \right ) } = { D y ’ \left ( x \right ) } = { y ^ { \prime \prime } \left ( x \right ) . } $$

به طریق مشابه، توان $$n$$اُم $$D$$، مشتق مرتبه $$n$$‌ را به دست می‌دهد:

$$ \large { D ^ n } y \left ( x \right ) = { y ^ { \left ( n \right ) } } \left ( x \right ) . $$

در اینجا فرض می‌کنیم می‌توان $$n$$ بار از تابع $$y(x)$$ مشتق گرفت.

عملگرهای دیفرانسیلی ممکن است بسته به توصیف دیفرانسیل پیچیده‌تر باشند؛ برای مثال، عملگر دیفرانسیلی نابلا (Nabla) اغلب در تحلیل برداری استفاده و به صورت زیر تعریف می‌شود:

$$ \large \nabla = \frac { \partial } { { \partial x } } \mathbf { i } + \frac { \partial } { { \partial y } } \mathbf { j } + \frac { \partial } { { \partial z } } \mathbf { k } $$

که در آن $$ \mathbf{i}$$، $$\mathbf{j} $$ و $$ \mathbf{k} $$ بردارهای یکه در طول محورهای مختصات $$x$$، $$y$$ و $$z$$ هستند.

در نتیجه اِعمال عملگر $$ \nabla $$ بر یک میدان اسکالر $$F$$،‌ گرادیان میدان برداری $$F$$ به دست می‌آید:

$$ \large { \nabla F } = { \frac { { \partial F } } { { \partial x } } \mathbf { i } + \frac { { \partial F } } { { \partial y } } \mathbf { j } } + { \frac { { \partial F } } { { \partial z } } \mathbf { k } . } $$

بردار گرادیان همیشه جهت بزرگترین افزایش تابع $$F$$ را نشان می‌دهد و طول آن، نرخ افزایش تابع را در این جهت مشخص می‌کند.

ضرب اسکالر یا ضرب داخلی بردار $$ \nabla$$ و میدان برداری $$ \mathbf{V} $$ به عنوان دیورژانس بردار $$ \mathbf{V} $$ شناخته می‌شود:

$$ \large { \nabla \cdot \mathbf { V } = \text {div} \, \mathbf { V } } = { \frac { { \partial { V _ x } } } { { \partial x } } + \frac { { \partial { V _ y } } } { { \partial y } } + \frac { { \partial { V _ z } } } { { \partial z } } . } $$

ضرب برداری دو بردار $$ \nabla$$ و $$ \mathbf{V} $$، کرل بردار $$ \mathbf{V} $$ را نتیجه می‌دهد:

$$ \large { \nabla \times \mathbf { V } = \text {rot} \, \mathbf { V } }
= { \left | { \begin {array} { * { 2 0 } { c } }
\mathbf { i } & \mathbf { j } & \mathbf { k } \\
{ \frac { \partial } { { \partial x } } } & { \frac { \partial } { { \partial y } } } & { \frac { \partial } { { \partial z } } } \\
{ { V _ x } } & { { V _ y } } & { { V _ z } }
\end{array} } \right | . } $$

ضرب نقطه‌ای $$ \nabla \cdot \nabla = {\nabla ^2} $$، متناظر با یک عملگر دیفرانسیلی اسکالر است که عملگر لاپلاس یا لاپلاسین نامیده شده و با نماد $$ \Delta $$ نشان داده می‌شود:

$$ \large { \Delta = { \nabla ^ 2 } } = { \frac { { { \partial ^ 2 } } } { { \partial { x ^ 2 } } } + \frac { { { \partial ^ 2 } } }{ { \partial { y ^ 2 } } } + \frac { { { \partial ^ 2 } } } { { \partial { z ^ 2 } } } . } $$

اکنون که با عملگرهای دیفرانسیلی آشنا شدیم، کاربرد این عملگر را در معادلات دیفرانسیل معرفی می‌کنیم.

عملگر دیفرانسیلی $$ \Large {L(D)}$$

معادله دیفرانسیل خطی مرتبه $$n$$ زیر را در نظر بگیرید:‌

$$ \large { { y ^ { \left ( n \right ) } } \left ( x \right ) } + { { a _ 1 } \left ( x \right ) { y ^ { \left ( { n – 1 } \right ) } } \left ( x \right ) + \cdots }
+ { { a _ { n – 1 } } \left ( x \right ) y ’ \left ( x \right ) } + { { a _ n } \left ( x \right ) y \left ( x \right ) } = { f \left ( x \right ) . } $$

فیلم آموزش معادلات دیفرانسیل به همراه حل سوالات آزمون کارشناسی ارشد در فرادرس

کلیک کنید

با استفاده از عملگر $$D$$، معادله دیفرانسیل بالا را می‌توان به صورت زیر نوشت:

$$ \large L \left ( D \right ) y \left ( x \right ) = f \left ( x \right )$$

که در آن، $$L(D)$$ چندجمله‌ای دیفرانسیل زیر است:

$$ \large { L \left ( D \right ) } = { { D ^ n } + { a _ 1 } \left ( x \right ) { D ^ { n – 1 } } + \cdots } + { { a _ { n – 1 } } \left ( x \right ) D } + { { a _ n } \left ( x \right ) . } $$

به‌ عبارت دیگر، عملگر $$L(D)$$، یک چندجمله‌ای جبری است که در آن، عملگر دیفرانسیلی $$D$$ نقش یک متغیر را بازی می‌کند.

در ادامه، چند ویژگی عملگر $$L(D)$$ را بررسی می‌کنیم:‌

۱. عملگر $$L(D)$$ خطی است:

$$ \large { L \left ( D \right ) \left [ { { C _ 1 } { y _ 1 } \left ( x \right ) + { C _ 2 } { y _ 2 } \left ( x \right ) } \right ] }
= { { C _ 1 } L \left ( D \right ) { y _ 1 } \left ( x \right ) } + { { C _ 2 } L \left ( D \right ) { y _ 2 } \left ( x \right ) . } $$

در حالتی که چند عملگر $$L(D)$$، $$M(D)$$ و $$N(D)$$ داشته باشیم (درجه چندجمله‌ای‌ها می‌تواند متفاوت باشد)، روابط زیر برقرار است:

۲. ویژگی جابه‌جاپذیری:

$$ \large { L \left ( D \right ) + M \left ( D \right ) } = { M \left ( D \right ) + L \left ( D \right ) . } $$

۳. ویژگی انجمنی یا شرکت‌پذیری:

$$ \large { \left [ { L \left ( D \right ) + M \left ( D \right ) } \right ] + N \left ( D \right ) }
= { L \left ( D \right ) + \left [ { M \left ( D \right ) + N \left ( D \right ) } \right ] . } $$

برای دو عملگر $$L(D)$$ و $$M(D)$$، عمل ضرب را می‌توان تعریف کرد:

$$ \large { \left [ { L \left ( D \right ) \cdot M \left ( D \right ) } \right ] y \left ( x \right ) } = { L \left ( D \right ) \cdot \left [ { M \left ( D \right ) y \left ( x \right ) } \right ] . } $$

لازم به ذکر است که عمل ضرب برای عملگرهای دیفرانسیلی با ضرایب ثابت، جابه‌جایی‌پذیر است؛ یعنی برای عملگرهایی به فرم $$  { L \left ( D \right ) } = { { D ^ n } + { a _ 1 } { D ^ { n – 1 } } + \cdots } + { { a _ { n – 1 } } D + { a _ n } } $$ که $$ {a_1}, \ldots ,{a_n} $$ اعداد ثابتی هستند، ویژگی‌های چهار تا شش برقرار است:‌

۴. قانون جابه‌جایی‌پذیری ضرب:

$$ \large { L \left ( D \right ) \cdot M \left ( D \right ) } = { M \left ( D \right ) \cdot L \left ( D \right ) } $$

۵. قانون شرکت‌‌پذیری ضرب:‌

$$ \large { { \left [ { L \left ( D \right ) \cdot M \left ( D \right ) } \right ] \cdot N } \kern0pt { \left ( D \right ) } }
= { { L \left ( D \right ) \cdot } \kern0pt { \left [ { M \left ( D \right ) \cdot N \left ( D \right ) } \right ] } } $$

۶. قانون توزیع ضرب روی جمع:

$$ \large { { L \left ( D \right ) \cdot } \kern0pt { \left [ { M \left ( D \right ) + N \left ( D \right ) } \right ] } }
= { L \left ( D \right ) \cdot M \left ( D \right ) } + { L \left ( D \right ) \cdot N \left ( D \right ) } $$

۷. یک ویژگی مفید دیگر عملگر $$D$$ به صورت زیر است:

$$ \large { D ^ m } { D ^ n } = { D ^ { m + n } } . $$

همان‌طور که می‌بینیم، عملگرهای دیفرانسیلی $$L(D)$$ با ضرایب ثابت، ویژگی‌های مشابهی با چندجمله‌های‌های جبری معمولی دارند. در نتیجه، مانند چندجمله‌ای‌های جبری، می‌توان عملگرهای $$L(D)$$ با ضرایب ثابت را ضرب و تقسیم کرد و از آن‌ها فاکتور گرفت. این ویژگی‌ها در حل معادلات دیفرانسیل مورد استفاده قرار می‌گیرند.

مثال‌ها

در ادامه،‌ چند مثال از عملگرهای دیفرانسیلی و کاربرد آن‌ها بیان می‌شود.

مثال ۱

صحت قانون جابه‌جاپذیری ضرب را برای عملگرهای $$ L = {D^2} + 1 $$ و $$ M = 2D +3 $$ تحقیق کنید.

حل: ابتدا $$ LMy $$ را محاسبه می‌کنیم:

$$ \large { M y = \left ( { 2 D + 3 } \right ) y } = { 2 y ’ + 3 y . } $$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

بنابراین، عبارت دیفرانسیلی زیر به دست می‌آید:‌

$$ \large { L M y = L \left ( { M y } \right ) }
= { \left ( { { D ^ 2 } + 1 } \right ) \left ( { 2 y ’ + 3 y } \right ) } \\ \large
= { 2 y ^ { \prime \prime \prime } + 3 y ^ { \prime \prime } + 2 y ’ + 3 y }
= { \left ( { 2 { D ^ 3 } + 3 { D ^ 2 } + 2 D + 3 } \right ) y . } $$

اکنون $$ MLy $$ را محاسبه می‌کنیم:

$$ \large { L y = \left ( { { D ^ 2 } + 1 } \right ) y } = { y ^ { \prime \prime } + y . } $$

بنابراین:

$$ \large { M L y = M \left ( { L y } \right ) }
= { \left ( { 2 D + 3 } \right ) \left ( { y ^ { \prime \prime } + y } \right ) } \\ \large
= { 2 y ^ { \prime \prime \prime } + 3 y ^ { \prime \prime } + 2 y ’ + 3 y }
= { \left ( { 2 { D ^ 3 } + 3 { D ^ 2 } + 2 D + 3 } \right) y . } $$

می‌بینیم که قانون جابه‌جایی‌پذیری ضرب برای این دو عملگر برقرار است (برای هر عملگر $$L(D)$$ با ضرایب ثابت برقرار است).

مثال ۲

صحت قانون جابه‌جاپذیری ضرب را برای عملگرهای $$ L = xD – 1 $$ و $$ M = {D^2} + {x^2} $$ تحقیق کنید.

حل: ابتدا عبارت دیفرانسیلی $$LMy$$ را محاسبه می‌کنیم:

$$ \large { M y = \left ( { { D ^ 2 } + { x ^ 2 } } \right ) y } = { y ^ { \prime \prime } + { x ^ 2 } y , } \\ \large { L M y = L \left ( { M y } \right ) }
= { \left ( { x D – 1 } \right ) \left ( { y ^ { \prime \prime } + { x ^ 2 } y } \right ) } \\ \large
= { { x y ^ { \prime \prime \prime } – y ^ { \prime \prime } } + { x \left ( { 2 x y + { x ^ 2 } y ’ } \right ) – { x ^ 2 } y } } \\ \large
= { { x y ^ { \prime \prime \prime } – y ^ { \prime \prime } + 2 { x ^ 2 } y } + { { x ^ 3 } y ’ – { x ^ 2 } y } } \\ \large
= { x y ^ { \prime \prime \prime } – y ^ { \prime \prime } + { x ^ 3 } y ’ + { x ^ 2 } y }
= { \left ( { x { D ^ 3 } – { D ^ 2 } + { x ^ 3 } D + { x ^ 2 } } \right ) y . } $$

به طریق مشابه،‌ $$MLy$$ را محاسبه و نتایج را مقایسه می‌کنیم:

$$ \large { L y = \left ( { x D – 1 } \right ) y } = { x y ’ – y ,} \require{cancel}
{ M L y = M \left ( { L y } \right ) } \\
= { \left ( { { D ^ 2 } + { x ^ 2 } } \right ) \left ( { x y ’ – y } \right ) }
= { { D \left ( { y ’ + x y ^ { \prime \prime } } \right ) } + { { x ^ 3 } y ’ – y ^ { \prime \prime } – { x ^ 2 } y } } \\ \large
= { { y ^ { \prime \prime } + \cancel { y ^ { \prime \prime } } + x y ^ { \prime \prime \prime } } - { \cancel { y ^ { \prime \prime } } + { x ^ 3 } y ’ – { x ^ 2 } y } } \\ \large
= { x y ^ { \prime \prime \prime } + y ^ { \prime \prime } + { x ^ 3 } y ’ – { x ^ 2 } y } = { \left ( { x { D ^ 3 } + { D ^ 2 } + { x ^ 3 } D – { x ^ 2 } } \right ) y . } $$

همان‌طور که می‌بینیم، عملگرهای $$L$$ و $$M$$ نتایج متفاوتی دارند. این عدم تشابه برای عملگرهایی با ضرایب متغیر، قابل انتظار است.

مثال ۳

یک جواب خصوصی معادله دیفرانسیل $$ y^{\prime\prime\prime} + 3y = {e^{2x}} $$ را با استفاده از روش عملگر بیابید.

حل: عملگر دلخواه $$L(D)$$ با ضرایب ثابت را در نظر بگیرید که به تابع نمایی $$ {e^{kx}} $$ اعمال می‌شود:

$$ \large { L \left ( D \right ) { e ^ { k x } } } = { \left ( { { k ^ n } + { a _ 1 } { k ^ { n – 1 } } + \cdots + { a _ n } } \right ){ e ^ { k x } } }
= { L \left ( k \right ) { e ^ { k x } } . } $$

در نتیجه می‌توان نوشت:

$$ \large L \left ( D \right ) \left [ { \frac { { { e ^ { k x } } } } { { L \left ( k \right ) } } } \right ] = { e ^ { k x } } . $$

از آن‌جایی که معادله دیفرانسیل به فرم عملگرِ

$$ \large L\left( D \right)y = {e^{kx}} $$

نوشته می‌شود، یکی از جواب‌ها تابع زیر خواهد بود:

$$ \large { y _ 1 } = \frac { { { e ^ { k x } } } } { { L \left ( k \right ) } } . $$

در این مثال، عملگر برابر است با:

$$ \large L \left ( D \right ) = { D ^ 3 } + 3 . $$

بنابراین، جواب خصوصی معادله دیفرانسیل به صورت زیر است:

$$ \large { { y _ 1 } = \frac { { { e ^ { k x } } } } { { L \left ( k \right ) } } = \frac { { { e ^ { k x } } } } { { { k ^ 3 } + 3 } } }
= { \frac { { { e ^ { 2 x } } } } { { { 2 ^ 3 } + 3 } } }
= { \frac { { { e ^ { 2 x } } } } { { 1 1 } } . } $$

مثال ۴

یک جواب خصوصی معادله دیفرانسیل $$ \large { y ^ { I V } } – y ^ { \prime \prime } + y = 2 \sin x $$ را با استفاده از روش عملگر بیابید.

حل: معادله را می‌توان به صورت زیر نوشت:‌

$$ \large { L \left ( D \right ) y = 2 \sin x\;\;} $$

یا

$$ \large \left ( { { D ^ 4 } – { D ^ 2 } + 1 } \right ) y = { 2 \sin x . } $$

این چندجمله‌‌ای دیفرانسیل فقط شامل جملاتی با توان‌های زوج $$D$$ است. با اعمال عملگر $$D^2$$ بر تابع $$ A\sin kx $$ داریم:

$$ \large { { D ^ 2 } y = { D ^ 2 } \left ( { A \sin k x } \right ) }
= { – { k ^ 2 } A \sin k x }
= { – { k ^ 2 } y . } $$

واضح است که برای چندجمله‌ای دیفرانسیل دلخواه $$ L\left( {{D^2}} \right) $$ با ضرایب ثابت، فرمول زیر برقرار است:‌

$$ \large { L \left ( { { D ^ 2 } } \right ) y } = { L \left ( { { D ^ 2 } } \right ) \left ( { A \sin k x } \right ) }
= { L \left ( { – { k ^ 2 } } \right ) A \sin k x }
= { L \left ( { – { k ^ 2 } } \right ) y . } $$

جواب خصوصی به صورت زیر است:

$$ \large { y _ 1 } = \frac { { A \sin k x } } { { L \left ( { – { k ^ 2 } } \right ) } } . $$

در این مثال، سمت راست معادله برابر با $$ 2\sin x $$ است و عملگر دیفرانسیل را می‌توان به صورت زیر نوشت:

$$ \large { L \left ( { { D ^ 2 } } \right ) } = { { \left ( { { D ^ 2 } } \right ) ^ 2 } – { D ^ 2 } + 1 . } $$

در نتیجه، پاسخ نهایی برابر است با:

$$ \large { { y _ 1 } = \frac { { A \sin k x } } { { L \left ( { – { k ^ 2 } } \right ) } } }
= { \frac { { A \sin k x } } { { { { \left ( { – { k ^ 2 } } \right ) } ^ 2 } – \left ( { – { k ^ 2 } } \right ) + 1 } } } \\ \large
= { \frac { { 2 \sin x } } { { { { \left ( { – { 1 ^ 2 } } \right ) } ^ 2 } – \left ( { – { 1 ^ 2 } } \right ) + 1 } } }
= { \frac { { 2 \sin x } } { 3 } . } $$