عدم قطعیت در کنترل و تخمین حالت — از صفر تا صد
در مطالب قبلی از مجله فرادرس به روشهای مختلف طراحی کنترلکننده مانند جبران ساز پیش فاز و پس فاز برای سیستمهای دینامیکی پرداختیم. متداولترین روشهای مورد استفاده مانند «روش جایابی قطب» (Pole Placement) در طراحی کنترل کننده و رویتگر یا «رگولاتورهای درجه دو خطی» (Linear Quadratic Regulators) همگی به اطلاعاتی راجع به دینامیک سیستم نیاز دارند. با این وجود، امکان ندارد که بتوان دینامیکهای سیستم را به صورت بسیار دقیق تخمین زد. به عبارت دیگر همواره مقداری عدم قطعیت» (Uncertainity) در سیستم کنترل وجود خواهد داشت. در این مطلب قصد داریم به بررسی عدم قطعیت در سیستم کنترل بپردازیم و سپس از قاعده بیز و فیلتر کالمن برای کنترل و تخمین حالتهای یک سیستم با عدم قطعیت استفاده کنیم.
عدم قطعیت در سیستم کنترل
همان طور که گفتیم، امکان تخمین کاملا دقیق حالتهای یک سیستم دینامیکی وجود ندارد. به عنوان مثال، هنگام مدلسازی یک سیستم واقعی مانند ربات، تعداد بسیار زیادی فرض آسان کننده در نظر گرفته میشود. اما در واقعیت اکثر این فرضها الزاما صحیح نیستند. جرم «رابط» (Link) تکی، موقعیت مرکز جرم، طول رابط و اینرسی لحظهای همگی توسط فرضهای ایده آل تخمین زده میشوند و در معرض خطای اندازهگیری قرار دارند.
یک منبع دیگر برای به وجود آمدن عدم قطعیت در سیستم، خطای مدلسازی است که میتواند از پدیدههای فیزیکی مانند اصطکاک ناشی شود و ممکن است به صورت کامل از آن صرف نظر شده باشد. وجود عدم قطعیت در سیستم کنترل میتواند منجر به این امر شود که محاسبات کنترل کننده و تخمین حالتها به صورت غلط انجام گیرد. در نتیجه وجود عدم قطعیت روی عملکرد مطلوب سیستم کنترلی تاثیر منفی میگذارد.
انواع عدم قطعیت
در ادامه میخواهیم انواع مختلف عدم قطعیت در سیستم کنترل را معرفی کنیم. یک سیستم را در نظر بگیرید که به صورت زیر مدلسازی شده است:
$$ \dot { X } = A X + B u $$
بردار خروجیها در این سیستم بر اساس معادله زیر به دست میآید:
$$ Y = C X $$
اما به این نکته توجه کنید که نمایش فوق، مدلی است که ما در حالت ایدهآل انتظار داریم سیستم بر اساس آن رفتار کند. در حالی که سیستم واقعی بسته به نوع عدم قطعیت آن، ممکن است به طریق متفاوتی نسبت به مدل فوق عمل کند. در حالت کلی میتوانیم عدم قطعیت را به چهار گروه اصلی تقسیم بندی کنیم:
- عدم قطعیت پارامتری (Parametric Uncertainity): این نوع از عدم قطعیت به وجود عدم قطعیت در پارامترهایی اشاره دارد که توصیف کننده مدل یک سیستم هستند. به عنوان مثال، در رابطه $$ F = M a $$، مدل توسط پارامتر M توصیف میشود. در حالتی که در مقدار یک پارامتر خطایی وجود داشته باشد، میتوان مدل واقعی سیستم و خروجی آن را به صورت زیر نوشت:
$$ \dot { X } = ( A + \Delta A) X + ( B + \Delta B) u $$
$$ y = ( C+ \Delta C ) X $$
- عدم قطعیت محرک (Actuator Uncertainity): عدم قطعیت در محرک یک سیستم ناشی از این واقعیت است که فرمان کنترلی صادر شده از کنترل کننده ممکن است به صورت کامل و دقیق اجرا نشود. این نوع از عدم قطعیت را میتوان به صورت زیر در مدل یک سیستم به حساب آورد:
$$ \dot { X } = A X + B ( u + \delta u) $$
$$ y = C X $$
- عدم قطعیت مدل (Modeling Uncertainity): عدم قطعیت مدل به خطایی اشاره دارد که به دلیل خود مدل به سیستم وارد میشود. به عنوان مثال میتوان کفت که خطاهایی مانند پدیده اصطکاک، خطای ناشی از «خطیسازی» (Linearization) و ... در این گروه از انواع عدم قطعیت جای میگیرند. مدل یک سیستم که دارای عدم قطعیت نوع مدل است را میتوان به صورت زیر نمایش داد:
$$ \dot { X } = A X + B u + f ( X , u ) $$
$$ y = C X + g ( X , u ) $$
- عدم قطعیت اندازهگیری (Measurement Uncertainity): این نوع از عدم قطعیت به وجود خطا در اندازهگیری اشاره دارد که به دلیل خطای سنسور و ادوات اندازهگیری به سیستم وارد میشوند. عدم قطعیت اندازهگیری را میتوان به صورت زیر در مدل سیستم نمایش داد:
$$ \dot { X } = A X + B u $$
$$ y = C X + \nu $$
حال در ادامه مطلب قصد داریم به بررسی دو روش کلی برای کنترل یک سیستم با وجود عدم قطعیت بپردازیم. در تکنیک اول فرض میشود که «اغتشاش» (Disturbance) دارای طبیعت گاوسی باشد، در حالی که روش دوم، مبتنی بر کمینه کردن پاسخ سیستم به ورود یک اغتشاش خارجی است. بر همین اساس، تکنیکها را میتوان به دو دسته گسترده زیر طبقه بندی کرد.
مدلسازی عدم قطعیت به عنوان یک فرایند گاوسی
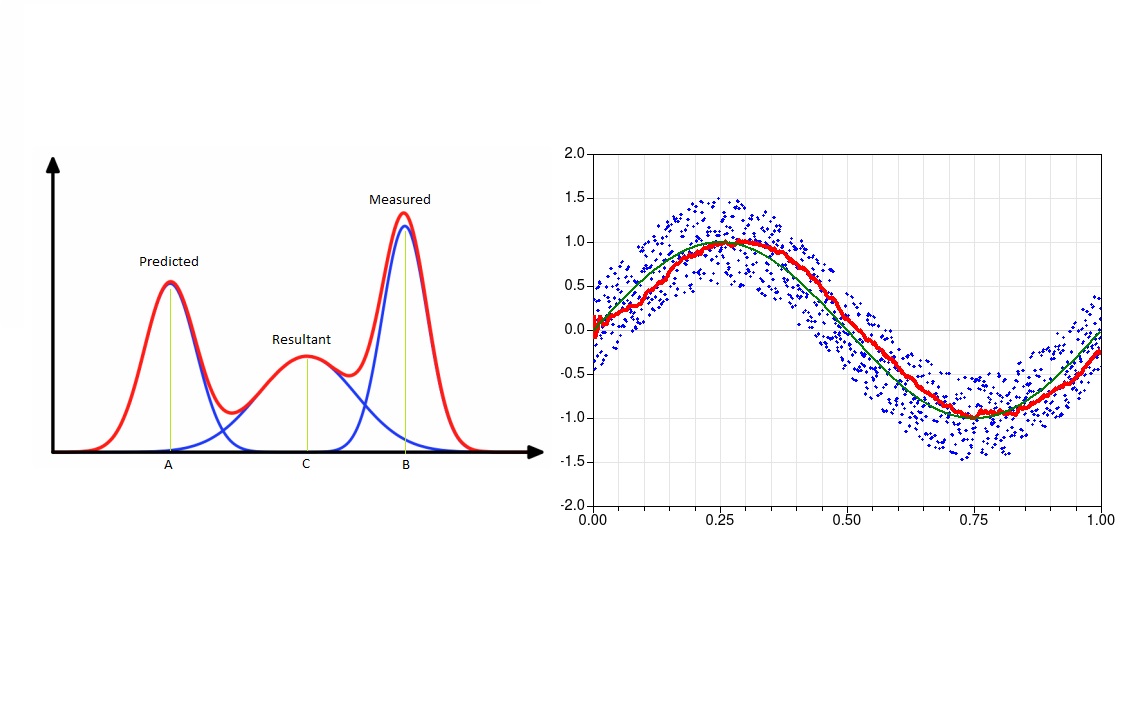
«فیلتر کالمن» (Kalman Filter) رویتگری است که بسیار شبیه به رگولاتور درجه دو خطی عمل میکند. در واقع فیلتر کالمن را با نام «برآوردگر درجه دو خطی» (Linear Quadratic Estimators) نیز میشناسند. فیلتر کالمن برای عملکرد خود به این فرض احتیاج ندارد که عدم قطعیت حتما باید یک فرایند گاوسی باشد. با این حال، اگر عدم قطعیت دارای طبیعت گاوسی باشد، آنگاه فیلتر کالمن به یک «فیلتر بهینه» (Optimal Filter) تبدیل میشود. تصویری از یک فرایند گاوسی در زیر نشان داده شده است.
روش دیگر مربوط به این طبقه، «کنترل گاوسی درجه دو خطی» (Linear Quadratic Gaussian Control) یا LQG است. کنترل LQG ترکیبی از برآوردگر درجه دو خطی (فیلتر کالمن) و رگولاتور درجه دو خطی به حساب میآید.
انتخاب کنترل کننده برای کمینه کردن حساسیت به عدم قطعیت
یکی از روشهای کنترلی که در گروه تکنیکهای کمینه کردن حساسیت به خطا قرار میگیرد، «کنترل H2» است. در کنترل H2، نرم H2 مربوط به سیستم (مجذور میانگین مربعات پاسخ فرکانسی) به ازای اغتشاش داده شده کمینه میشود. به عبارت دیگر، کنترل کننده به نحوی طراحی میشود که حساسیت سیستم که به صورت H2 اندازهگیری میشود، کمینه شود.
روش کنترل ∞ - H نیز یکی دیگر از روشهای کنترلی این گروه است. نرم ∞ - H به بزرگترین مقدار دامنه مربوط به پاسخ ناشی از اعمال اغتشاش اشاره دارد. در کنترل ∞ - H، کنترل کننده به نحوی انتخاب میشود که نرم ∞ - H پاسخ کمینه شود.
فیلتر کالمن
در ادامه ابتدا به بررسی فیلتر کالمن میپردازیم و ایده اصلی مربوط به کنترل بهینه سیستم در صورت وجود عدم قطعیت را از آن استخراج میکنیم. اصول کاری یک فیلتر کالمن به این صورت است که اطلاعات مربوط به دینامیک سیستم را با اندازهگیریهای قبلی ترکیب میکند و به این ترتیب حالت کنونی سیستم را تقریب میزند. عملکرد یک فیلتر کالمن بسیار بهتر از شرایطی است که فقط از اندازهگیریهای قبلی و یا فقط از حالتهای کنونی استفاده شود.
این مفاهیم را میتوان از طریق ارائه یک مثال به صورت واضحتر بیان کرد. فرض کنید میخواهیم موقعیت یک خودرو را تخمین بزنیم که با سرعتی ثابت در راستای یک خط راست در حال حرکت است. ممکن است در جهتدهی فرمان، اختلاف بین سرعت واقعی و سرعت مطلوب خودرو و نیز در اندازهگیریهای به دست آمده از خودرو مقداری خطا وجود داشته باشد. این خطاها در به دست آوردن موقعیت خودرو ابهاماتی به وجود میآورند. اگر فرض کنیم که موقعیت و سرعت خودرو یک فرایند گاوسی را دنبال میکنند، آنگاه میتوانیم ناحیهای را به دست آوریم که انتظار داریم خودرو در آن قرار داشته باشد. این مفهوم در تصویر متحرک زیر نشان داده شده است.

در انیمیشن فوق، تخمین محل قرار گرفتتن خودرو توسط یک ابر قرمز رنگ نشان داده شده است. در ابتدا موقعیت و سرعت نسبی خودرو را میدانیم. هنگامی که خودرو شروع به حرکت میکند، به دلیل تعقیب نادقیق سرعت، خطای زاویه فرمان، خطای محرک و ... مقداری خطا به مدل سیستم وارد میشود. تمام این موارد منجره به کاهش دقت و اعتماد ما در یافتن موقعیت دقیق و مطمئن خودرو میشوند. بنابراین، هنگامی که خودرو حرکت میکند، ناحیه تخمینی برای موقعیت خودرو که میتواند در آن جا قرار داشته باشد، افزایش مییابد.
با این حال، زمانی که اندازهگیری موقعیت را به دست آوریم، میتوانیم موقعیت خودرو را آپدیت کنیم. البته به این نکته باید توجه کرد که اندازهگیری خود دقیق نیست و همواره مقداری عدم قطعیت از نوع اندازهگیری در خود دارد. بنابراین موقعیت خودرو را فقط در یک ناحیه میتوان تخمین زد.
احتمالات
فیلترهای کالمن مبتنی بر ایده استنتاج بیز هستند. استنتاج بیز یک روش آماری است که در آن تا زمانی که اطلاعات و شواهد در دست باشند، احتمال درست بودن یک فرضیه به صورت پیوسته آپدیت میشود. استنتاج بیز مبتنی بر تئوری بیز است که در آن احتمال یک پدیده بر اساس ویژگیهای مرتبط به آن محاسبه میشود. به عنوان مثال، اگر بیماری فراموشی، با سن ارتباط داشته باشد، آنگاه با استفاده از تئوری بیز، میتوان از سن فرد برای پیشبینی این احتمال استفاده کرد که آیا او به بیماری فراموشی دچار خواهد شد یا خیر.
به عبارت دیگر، تئوری بیز پیشبینی سن را به احتمال درست بودن فرضیه (فراموشی) ربط میدهد. قانون بیز را میتوان به صورت رابطه زیر بیان کرد:
$$ P ( A | B ) = \frac { P ( B | A ) P ( A ) } { P ( B ) } $$
توجه کنید که پدیده A به شرط B و یا پدیده B به شرط A فقط زمانی اتفاق میافتند که هم A و هم B رخ بدهند. بنابراین تئوری بیز را گاهی میتوان به صورت زیر نیز نوشت:
$$ P ( A | B ) P ( B ) = P ( B | A ) P ( A ) = P ( A \cap B) $$
یک راه دیگر، نوشتن رابطه بیز به صورت زیر است:
$$ P ( A | B) = \frac { P ( B | A ) P ( A ) } { P ( B | A ) P ( A ) + P ( B | \neg A ) P ( \neg A ) } $$
در رابطه فوق، $$ \neg A $$ برای نشان دادن قرینه یا Not پدیده A مورد استفاده قرار گرفته است.
اگر پدیده A بتواند چند مقدار را به خود اختصاص دهد، مثلا $$ A _ i $$ به ازای $$ i : 1 \rightarrow N $$، آنگاه داریم:
$$ P ( A | B ) = \frac { P ( B | A ) P ( A ) } { \sum _ { i = 1 } ^ N P ( B | A _ i ) P ( A _ i) } , $$
در ادامه از طریق دو مثال قضیه بیز را بیشتر توضیح خواهیم داد.
مثال ۱: تشخیص سرطان
فرض کنید یک آزمایش برای تست بیماری سرطان وجود دارد که ۹۹ درصد دقت دارد. به عبارت دیگر، اگر یک فرد بیماری سرطان داشته باشد، آنگاه نتیجه تست با احتمال ۹۹ درصد مثبت خواهد بود. این مقدار را تحت عنوان «نرخ درست - مثبت» (True-Positive Rate) یا «حساسیت» (Sensitivity) نیز میشناسند. از طرف دیگر، اگر فردی سالم باشد و سرطان نداشته باشد، نتیجه تست به احتمال ۹۸ درصد منفی خواهد بود. به این مقدار نیز «نرخ صحیح - منفی» (True Negative Rate) یا «تشخیص پذیری» (Specificity) میگویند. با دانستن این که بیماری سرطان یک بیماری نادر است و فقط ۱٫۵ درصد از جمعیت جهان به آن مبتلا میشوند، اگر نتیجه تست برای یک نفر مثبت باشد، آنگاه احتمال اینکه آن فرد واقعا به این بیماری مبتلا باشد چقدر است؟
حل:
در این سوال میخواهیم احتمال $$ P ( C | + ) $$ را به دست آوریم که C نشان دهنده سرطان، NC نشان دهنده عدم سرطان، «-»نشان دهنده نتیجه منفی تست و «+» نشان دهنده نتیجه مثبت تست است. حال میتوان اطلاعات داده شده درباره بیماری و نیز آزمایش را به صورت زیر نوشت:
- حساسیت = ۹۹ درصد، بنابراین $$ P ( + | C ) = 0 . 99 $$ است.
- تشخیص پذیری = ۹۸ درصد، بنابراین $$ P ( - | N C ) = 0.98 $$ است.
- احتمال سرطان = 0.015 درصد، بنابراین $$ P ( C ) = 0 . 015 $$ است.
با استفاده از قاعده بیز، رابطه زیر صادق است:
$$ P ( C | + ) = \frac { P ( + | C ) P ( C ) } { P ( + | C) P ( C ) + P ( + | N C ) P ( N C ) } $$
در رابطه فوق، دو مقدار $$ P ( +| N C ) $$ و $$ P ( N C ) $$ را در اختیار نداریم. برای محاسبه این دو مقدار به صورت زیر عمل میکنیم:
$$ P ( +| N C ) = 1 - P ( - | N C) = 1 - 0 . 98 = 0 . 0 2 $$
$$ P ( N C ) = 1 - P ( C ) = 1 - 0 . 0 1 5 = 0 . 9 8 5 $$
حال میتوانیم احتمال درست بودن یک نتیجه تست مثبت را به صورت زیر به دست آوریم:
$$ P ( C | + ) = \frac { . 9 9 \times 0 . 0 1 5 } { . 9 9 \times 0 . 0 1 5 + . 0 2 \times 0 . 9 8 5 } = 0 . 4 3 $$
بنابراین، با وجود داشتن حساسیت ۹۹ درصد و تشخیص پذیری ۹۸ درصد در آزمایش، اما به دلیل شیوع بسیار پایین این بیماری، یک پاسخ مثبت آزمایش فقط ۴۳ درصد احتمال درست بودن دارد.
مثال ۲: تخمین بیز
قاعده بیز را میتوان به یک توزیع احتمالاتی نیز اعمال کرد. توزیع احتمالاتی زمانی مورد استفاده قرار میگیرد که یک پدیده نتواند به صورت یک کمیت منفرد یا یکتا (Singular) تقریب زده شود و چندین وضعیت محتمل وجود داشته باشد که بتواند در آنها قرار بگیرد.
سناریو ۱
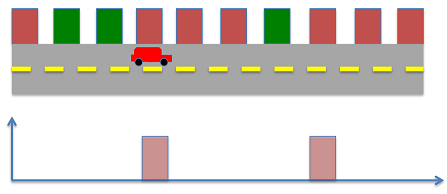
تصور کنید که یک ربات مانند تصویر زیر در راستای یک جاده حرکت میکند.
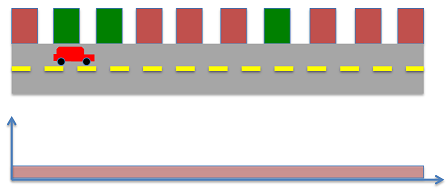
موقعیت ساختمانها (بلوکهای سبز و قرمز در تصویر) در دنیای واقعی را میدانیم و سنسورهایی برای تشخیص رنگهای سبز و قرمز ساختمانهای مجاور جاده در اختیار داریم. فرض کنید هیچ اطلاعاتی برای شروع نداریم. در نتیجه تمام مکانها دارای احتمال یکسان (1/10) هستند. این احتمال به صورت زیر بیان میشود:
$$ P ( X ) ^ - = \left [ \begin {array} { cc c c c c c c c c } 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 \end {array} \right] $$
به این احتمال، «احتمال پیشین» (Prior Probability) نیز میگویند؛ زیرا این احتمال قبل از هر گونه اندازهگیری به دست آمده است. فرض کنید ربات یکی از رنگهای سبز یا قرمز را تشخیص داده باشد و سنسور دارای اندازهگیری ایدهآل باشد. آنگاه احتمال اندازهگیری رنگ سبز توسط فرمول زیر نشان داده میشود:
$$ P _ g ( X ) = P ( g | X ) = \left [ \begin {array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] $$
به طریق مشابه، احتمال اندازهگیری رنگ قرمز به صورت زیر است:
$$ P _ r ( X ) = P ( r | X ) = \left [ \begin {array} { c c c c c c c c c c } 1 / 7 & 0 & 0 & 1 / 7 & 1 / 7 & 1 / 7 & 0 & 1 / 7 & 1 / 7 & 1 / 7 \end {array} \right] $$
حال پس از حرکت ربات و اندازهگیری محیط توسط سنسور، یک ساختمان سبز رنگ تشخیص داده میشود. احتمال بعد از اندازهگیری را میتوان توسط قاعد بیز به دست آورد. به احتمال پس از اندازهگیری، «احتمال پسین» (Posteriror Probability) میگویند. بر اساس قاعده بیز به رابطه زیر دست مییابیم:
$$ P ( X ) ^ + = P ( X | g ) = \frac { P ( g | X ) P ( X ) ^ - } { P ( g ) } = \frac { P ( g | X ) P ( X ) } { \sum _ { i = 1 } ^ N P ( g | X _ i ) P (X _ i ) } $$
$$ P ( X ) ^ + = P ( X | g ) = \frac { \left [ \begin {array}{ c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] \circ }{ \sum ( \left[ \begin {array}{ c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] \circ } \\
\frac {\left[ \begin {array} { c c c c c c c c c c } 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 \end {array} \right]} { \left[ \begin{array} { c c c c c c c c c c } 0.1 & 0.1 & 0.1 & 0.1 & 0.1 & 0.1 & 0.1 & 0.1 & 0.1 & 0.1 \end{array} \right] ) } $$
بر اساس رابطه فوق، با نماد $$ \circ $$، المانهای بردار اندازهگیری اولیه در المانهای بردار احتمال اندازهگیریها ضرب میشود.
در نتیجه احتمال پسین یا احتمال پس از اندازهگیری به صورت زیر محاسبه میشود:
$$ P ( X ) ^ + = P ( X | g ) = \frac { \left [ \begin {array} { c c c c c c c c c c } 0 & .1 / 3 & .1 / 3 & 0 & 0 & 0 & .1 / 3 & 0 & 0 & 0 \end{array} \right] } { \sum \left ( \left[ \begin{array}{ c c c c c c c c c c } 0 & . 1 / 3 & . 1 / 3 & 0 & 0 & 0 & .1 / 3 & 0 & 0 & 0 \end{array} \right] \right ) } $$
در نهایت احتمال پسین یا احتمال بعد از اندازهگیری به صورت زیر به دست میآید:
$$ P ( X ) ^ + = P ( X | g ) = \left [ \begin{array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] $$
اگر ربات مجبور باشد در یک موقعیت ثابت باقی بماند و به اندازهگیری ادامه دهد، مقدار سبز را به صورت تکراری هر بار اندازه میگیرد و موقعیت احتمالی آن آپدیت نمیشود. اما با حرکت در محیط و اندازهگیری، ربات میتواند تخمین بهتری را از موقعیت خود به دست آورد. فرض کنید که ربات یک گام گسسته به جلو حرکت کند. موقعیت احتمالی ربات و احتمال آن به صورت زیر است.
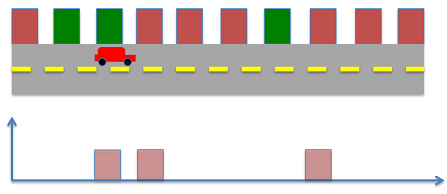
موقعیت احتمالی ربات و احتمال آن به صورت زیر به دست میآید:
$$ P ( X ) ^ - = \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 \end {array} \right] $$
ربات در این حالت اندازهگیری دیگری را انجام میدهد و خود را نزدیک به یک در سبز رنگ میبیند. احتمال اندازهگیری یک در سبز رنگ به صورت زیر است:
$$ P _ g ( X ) = P ( g | X ) = \left [ \begin {array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] $$
بر این اساس، میتوانیم احتمال پسین را مجددا محاسبه کنیم:
$$ P ( X ) ^ + = P ( X | g ) = \frac { P ( g | X ) P ( X ) ^ - } { P ( g ) } = \frac { P ( g | X ) P ( X ) } { \sum _ { i = 1 } ^ N P ( g | X _ i ) P ( X _ i ) } $$
حال احتمال اندازهگیری و احتمال پیشین را از بالا جایگذاری میکنیم:
$$P ( X ) ^ + = \frac { \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 1/3 & 1/3 & 0 & 0 & 0 & 1/3 & 0 & 0 \end {array} \right] \circ }{ \sum ( \left[ \begin {array} { c c c c c c c c c c } 0 & 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 \end {array} \right] \circ } \\
\frac { \left[ \begin {array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] } { \left[ \begin {array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] ) } $$
$$ P ( X ) ^ + = \frac { \left [ \begin {array} { c c c c c c c c c c } 0 \times 0 & 0 \times 1 / 3 & 1 / 3 \times 1 / 3 & 1 / 3 \times 0 & 0 \times 0 & 0 \times 0 & 0 \times 1 / 3 & 1 / 3 \times 0 & 0\times 0 & 0 \times 0 \end {array} \right] } { \sum \left ( \left [ \begin {array} { c c c c c c c c c c } 0 \times 0 & 0 \times 1 / 3 & 1 / 3 \times 1 / 3 & 1 / 3 \times 0 & 0 \times 0 & 0 \times 0 & 0 \times 1 / 3 & 1 / 3 \times 0 & 0 \times 0 & 0 \times 0 \end {array} \right] \right)} $$
$$ P ( X ) ^ + = \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end {array} \right] $$
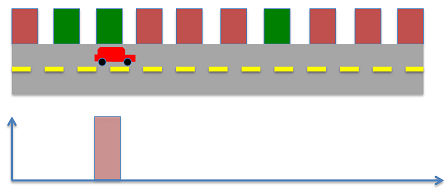
سناریو ۲
یک سناریو را در نظر بگیرید که در آن ربات در مکانهای مختلفی شروع به حرکت میکنند. مانند حالت قبل، ما موقعیت ساختمانهای قرمز و سبز در دنیای واقعی را میدانیم. در تصویر زیر نمایی از این حالت نشان داده شده است. همچنین در این سیستم سنسورهایی برای تشخیص رنگ سبز و قرمز ساختمانهای نزدیک خودرو وجود دارد. همانند حالت قبلی، احتمال اندازهگیری رنگ سبز به صورت زیر است:
$$ P _ g ( X ) = P ( g | X ) = \left [ \begin {array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right ] $$
همچنین احتمال اندازهگیری رنگ قرمز به صورت زیر نوشته میشود:
$$ P _ r ( X ) = P ( r | X ) = \left [ \begin {array} { c c c c c c c c c c } 1 / 7 & 0 & 0 & 1 / 7 & 1 / 7 & 1 / 7 & 0 & 1 / 7 & 1 / 7 & 1 / 7 \end {array} \right] $$
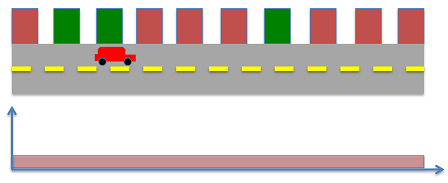
به دلیل این که موقعیت شروع حرکت ربات را نمیدانیم، احتمال پیشین به صورت زیر به دست میآید:
$$
P ( X ) ^ - = \left [ \begin {array} { c c c c c c c c c c } 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 & 0 . 1 \end {array} \right] . $$
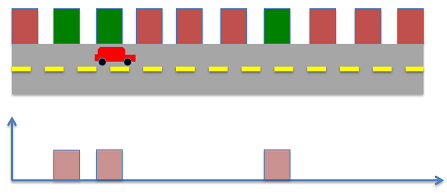
حال ربات شروع به اندازهگیری محیط میکند و یک در سبز رنگ را میبیند. احتمال بعد از اندازهگیری را میتوان همانند قبل با استفاده از قاعده بیز محاسبه کرد:
$$ P ( X ) ^ + = P ( X | g ) = \frac{ P ( g | X ) P ( X ) ^ - } { P ( g ) } = \frac { P ( g | X ) P ( X ) } { \sum _ { i = 1 } ^ N P ( g | X _ i ) P ( X _ i ) } $$
$$ P ( X ) ^ + = P ( X | g ) = \left [ \begin {array} { c c c c c c c c c c } 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 & 0 \end {array} \right] $$
نمایی از این حالت در تصویر زیر نشان داده شده است.
ربات به سمت جلو حرکت میکند و احتمال پیشین به صورت زیر نوشته خواهد شد:
$$ P ( X ) ^ - = \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 \end {array} \right] $$
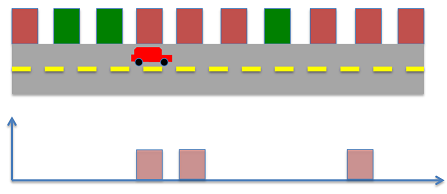
ربات مجددا محیط را اندازهگیری میکند و این بار به جای رنگ سبز، یک در قرمز رنگ را تشخیص میدهد. احتمال پسین به صورت زیر باید محاسبه شود:
$$ P ( X ) ^ + = P ( X | r ) = \frac { P ( r | X ) P ( X ) ^ - } { P ( r ) } = \frac { P ( r | X ) P ( X ) } { \sum _ { i = 1 } ^ N P ( r | X _ i ) P ( X _ i ) } $$
$$ P ( X ) ^ + = \frac { \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 \end {array} \right] \circ } { \sum ( \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 1 / 3 & 1 / 3 & 0 & 0 & 0 & 1 / 3 & 0 & 0 \end {array} \right] \circ } \\
\frac { \left [ \begin {array} { c c c c c c c c c c } 1 / 7 & 0 & 0 & 1 / 7 & 1 / 7 & 1 / 7 & 0 & 1 / 7 & 1 / 7 & 1 / 7\end {array} \right] } { \left [ \begin {array} { c c c c c c c c c c } 1 / 7 & 0 & 0 & 1 / 7 & 1 / 7 & 1 / 7 & 0 & 1 / 7 & 1 / 7 & 1 / 7\end {array} \right] ) } $$
$$
P ( X ) ^ + = \frac { \left [ \begin {array} { c c c c c c c c c c } 0 \times 1 / 7 & 0 \times 0 & 1 / 3 \times 0 & 1 / 3\times 1 / 7 & 0 \times 0 & 0 \times 0 & 0 \times 0 & 1 / 3 \times 1 / 7 & 0 \times 1 / 7 & 0 \times 1 / 7 \end {array} \right] } { \sum \left ( \left [ \begin {array} { c c c c c c c c c c } 0 \times 1 / 7 & 0 \times 0 & 1 / 3 \times 0 & 1 / 3 \times 1 / 7 & 0 \times 0 & 0 \times 0 & 0 \times 0 & 1 / 3 \times 1 / 7 & 0 \times 1 / 7 & 0 \times 1 / 7 \end {array} \right] \right)} $$
$$ P ( X ) ^ + = \frac { \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 0 & 1 / 2 1 & 0 & 0 & 0 & 1 / 2 1 & 0 & 0 \end{array} \right] } { \sum \left( \left [ \begin {array}{ c c c c c c c c c c } 0 & 0 & 0 & 1 / 21 & 0 & 0 & 0 & 1 / 21 & 0 & 0 \end {array} \right] \right) } =\\
\frac { \left[ \begin {array}{ c c c c c c c c c c } 0 & 0 & 0 & 1 / 2 1 & 0 & 0 & 0 & 1 / 2 1 & 0 & 0 \end {array} \right] } { 2 / 2 1 } $$
$$ P ( X ) ^ + = \left [ \begin {array} { c c c c c c c c c c } 0 & 0 & 0 & 1 / 2 & 0 & 0 & 0 & 1 / 2 & 0 & 0 \end {array} \right] $$
بنابراین در این حالت، دانش ربات درباره موقعیت خودش را بهتر میتوان به یکی از دو موقعیت در محیط تخمین زد. با این حال، با تکرار چند باره فرایند حرکت و اندازهگیری، ربات میتواند به تدریج موقعیت خود را بیاموزد.
فرایندی که در بالا به توصیف آن پرداختیم، ایده اساسی تخمین بیز است. در محاسبات فوق، فرض کردهایم که حرکت ربات و سنسورها ایدهآل هستند. به عبارت دیگر، اگر ربات تلاش کند که یک گام به جلو حرکت کند، در واقعیت نیز یک گام به جلو خواهد رفت. در حالی که در کاربردهای عملی، ممکن است تعداد زیادی پارامتر عدم قطعیت وجود داشته باشند که مانع از انجام این فرایند شوند و ما فقط میتوانیم تعیین کنیم که با چه احتمالی ربات قادر به حرکت خواهد بود.
در این حالت، حرکت را با یک مقدار احتمالاتی بیان میکنیم و توزیع احتمالاتی معین به یک توزیع چند متغیره تبدیل خواهد شد. به طریق مشابه، در سنسور و اندازهگیریهای آن نیز ممکن است خطا وجود داشته باشد و مقادیر اشتباهی از کمیتها توسط سنسور ارايه شود. توجه کنید که این مورد نیز به عدم قطعیتها افزوده میشود و روی مسطح شدن توزیع احتمالاتی تاثیر می گذارد، به عبارت دیگر، قطعیت ربات در یک بازه کاهش مییابد.
قاعده بیز برای توزیع گاوسی
توزیع گاوسی یا توزیع نرمال، یک توزیع احتمالاتی پیوسته بسیار متداول است. توزیع گاوسی یا نرمال به دلیل «قضیه حد مرکزی» (Central Limit Theorem) بسیار مورد استفاده قرار میگیرد. بر اساس قضیه حد مرکزی، تحت فرضهای خاصی، زمانی که تعداد نمونهها بسیار بزرگ شوند، میانگین نمونههای تصادفی از هر توزیع داده شده به یک توزیع گاوسی یا نرمال همگرا میشوند. اکثر پدیدههای فیزیکی ترکیبی از چند فرایند مستقل هستند و معمولا به توزیع نرمال گاوسی نزدیک هستند. به علاوه، بسیاری از روشها مانند انتشار عدم قطعیت و یا برازش حداقل مربعات پارامترها را میتوان زمانی که متغیرهای مرتبط دارای توزیع نرمال هستند، به صورت تحلیلی و به فرم ضمنی به دست آورد.
توزیع نرمال را به فرم یک منحنی زگولهای نمایش میدهند. «تابع چگالی احتمال» (Probability Density Function) را میتوان به صورت زیر نمایش داد:
$$ f ( X | \mu , \sigma ^ 2 ) = \frac { 1 } { \sqrt { 2 \pi \sigma ^ 2 } } e ^ { - \frac { ( X - \mu ) ^ 2 } { 2 \sigma ^ 2 } } $$
در رابطه فوق، $$ \mu $$ برابر با میانگین دادهها و $$ \sigma $$ انحراف معیار توزیع دادهها است.
با اجرای برنامه متلب زیر شکل این توزیع احتمالاتی را ترسیم خواهیم کرد.
1clc
2close all
3clear all
4
5X = -10:0.01:10;
6mu = 0;
7sigma = 1.25;
8f_x = 1/sqrt(2*pi*sigma^2) * exp( -(X-mu).^2/(2*sigma^2) );
9figure;
10plot(X,f_x)
11axis([-10 10 0 .4])
12xlabel('X')
13ylabel('Probability distribution')خروجی برنامه به صورت زیر است.
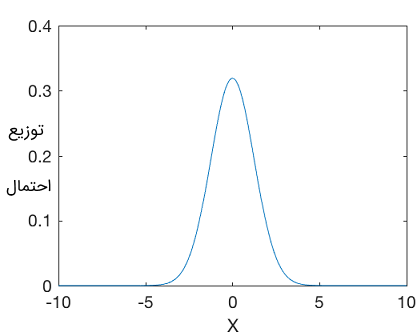
همان طور که میدانیم، تخمین بیز میتواند از طریق ضرب کردن توزیعهای احتمالاتی محاسبه شود. اگر نویز سنسور و فرایند حرکت را بتوان به صورت یک توزیع گاوسی توصیف کرد، آنگاه میتوان موقعیت احتمالی ربات را با استفاده از تکنیکهای قبلی به دست آورد. با این حال، این فرایند شامل محاسبه حاصل ضرب توزیعهای احتمالاتی است. دو توزیع احتمالاتی نرمال را در نظر بگیرید که با رابطه زیر توصیف میشوند:
$$ f ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) = \frac { 1 } { \sqrt { 2 \pi \sigma _ 1 ^ 2 } } e ^ { - \frac { ( X - \mu _ 1 ) ^ 2 } { 2 \sigma _ 1 ^ 2 } } $$
$$ f ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) = \frac { 1 } { \sqrt { 2 \pi \sigma _ 2 ^ 2 } } e ^ { - \frac { ( X - \mu _ 2 ) ^ 2 } { 2 \sigma _ 2 ^ 2 } } $$
احتمال بیز به صورت زیر محاسبه میشود:
$$ f ( ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) | ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) ) = \frac { f ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) f ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) } { \int _ { - \infty } ^ { \infty } f ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) f ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) d X } $$
حاصل ضرب دو تابع احتمالاتی به صورت زیر به دست میآید:
$$ \large f ( ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) | ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) ) = \frac { 1 } { \sqrt { 2 \pi \sigma _ 1 ^ 2 } } e ^ { - \frac { ( X - \mu _ 1 ) ^ 2 } { 2 \sigma _ 1 ^ 2 } } \frac { 1 } { \sqrt { 2 \pi \sigma _ 2 ^ 2 } } e ^ { - \frac { ( X - \mu _ 2 ) ^ 2 } { 2 \sigma _ 2 ^ 2 } } $$
$$ \large f ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) | f ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) = \frac { 1 } { \sqrt { 4 \pi ^ 2 \sigma _ 1 ^ 2 \sigma _ 2 ^ 2 } } e ^ { - \left [ \frac { ( X - \mu _ 1 ) ^ 2 } { 2 \sigma _ 1 ^ 2 } + \frac { ( X - \mu _ 2 ) ^ 2 } { 2 \sigma _ 2 ^ 2 } \right ] } $$
$$ \large f ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) | f ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) = \frac { 1 } { \sqrt { 4 \pi ^ 2 \sigma _ 1 ^ 2 \sigma _ 2 ^ 2 } } e ^ { - \left [ \frac { ( \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 ) X ^ 2 - 2 ( \mu _ 1 \sigma _ 2 ^ 2 + \mu _ 2 \sigma _ 1 ^ 2 ) X + ( \mu _ 1 ^ 2 \sigma _ 2 ^ 2 + \mu _ 1 ^ 2 \sigma _ 1 ^ 2 ) } { 2 \sigma _ 1 ^ 2 \sigma _ 2 ^ 2 } \right ] } $$
حال پس از سادهسازی به نتیجه زیر میرسیم:
$$ f ( X | \mu _ 1 , \sigma _ 1 ^ 2 ) | f ( X | \mu _ 2 , \sigma _ 2 ^ 2 ) = f ( X | \mu _ { 1 2 } , \sigma _ { 1 2 } ^ 2 ) = \frac { 1 }{ \sqrt { 2 \pi \sigma _ { 1 2 } ^ 2 } } e ^ { - \frac { ( X -\mu _ { 1 2 } ) ^ 2 } { 2 \sigma _ { 1 2 } ^ 2 } } $$
در رابطه فوق داریم:
$$ \sigma _ { 1 2 } ^ 2 = \frac { \sigma _ 1 ^ 2 \sigma _ 2 ^ 2 }{ \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 } $$
$$ \mu _ { 1 2 } = \frac { \sigma _ 1 ^ 2 \mu _ 2 + \sigma _ 2 ^ 2 \mu _ 1 } { \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 } $$
روابط بالا نشان میدهد که کانولوشن نرمالیزه شده دو توزیع گاوسی خود یک توزیع گاوسی دیگر است که انحراف معیار آن برابر با «میانگین هارمونیک» (Harmonic Mean) دو توزیع و میانگین توزیع حاصل، توسط معکوس واریانسهای آنها وزندار شده است.
این امر منجر به یک توزیع میشود که در آن میانگین به سمت توزیعی با انحراف معیار پایینتر حرکت خواهد کرد. به علاوه، واریانس ترکیب شده برابر با معکوس مجموع معکوس واریانس دو توزیع خواهد بود. بنابراین، واریانس به دست آمده کمتر از واریانس هر کدام از توزیعها است. در یک مورد خاص، زمانی که واریانس توزیعهای اصلی با یکدیگر برابر هستند، واریانس توزیع ترکیب شده برابر با نصف واریانس هر کدام از توزیعها خواهد بود. این مفهوم در مثال زیر توضیح داده شده است.
مثال 1: احتمال ترکیبی گاوسی
فرض کنید دو توزیع گاوسی با میانگین و انحراف معیار زیر در اختیار داشته باشیم:
$$ \sigma _ 1 = . 8 , \mu _ 1 = 2 $$
$$ \sigma _ 2 = . 5 , \mu _ 2 = 4 $$
همچنین داشته باشیم:
$$ \sigma _ { 1 2 } ^ 2 = \frac { \sigma _ 1 ^ 2 \sigma _ 2 ^ 2 } { \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 } = 3 . 2 $$
و
$$ \mu _ { 1 2 } = \frac { \sigma _ 1 ^ 2 \mu _ 2 + \sigma _ 2 ^ 2 \mu _ 1 } { \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 } = 0.66 . $$
این توزیعهای احتمالاتی را در متلب ترسیم میکنیم. برای این کار کد زیر را باید اجرا کرد:
1clc;close all;clear all
2
3X = -10:0.01:10;
4mu1 = .8 ; sigma1 = 2;
5mu2 = .1 ; sigma2 = 4;
6
7mu12 = (sigma1^2*mu2 + sigma2^2*mu1)/(sigma1^2 + sigma2^2);
8sigma12 = sqrt((sigma1^2*sigma2^2)/(sigma1^2 + sigma2^2));
9
10display(['\mu_{12} = ' num2str(mu12) ', \sigma_{12} = ' num2str(sigma12)] )
11
12f1 = 1/sqrt(2*pi*sigma1^2) * exp( -(X-mu1).^2/(2*sigma1^2) );
13f2 = 1/sqrt(2*pi*sigma2^2) * exp( -(X-mu2).^2/(2*sigma2^2) );
14f12 = 1/sqrt(2*pi*sigma12^2) * exp( -(X-mu12).^2/(2*sigma12^2) );
15figure;
16plot(X,f12,X,f1,'g--',X,f2,'g--')
17axis([-10 10 0 .4])
18xlabel('X')
19ylabel('Probability distribution')نتیجه به صورت زیر خواهد بود.
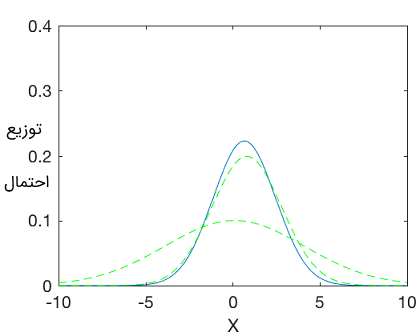
1\mu_{12} = 0.66, \sigma_{12} = 1.7889مثال ۲: احتمال ترکیبی گاوسی
این بار دو توزیع گاوسی با میانگین و انحراف معیار زیر را در نظر بگیرید:
$$ \sigma _ 1 = 2 , \mu _ 1 = -4 $$
$$ \sigma _ 2 = 2 , \mu _ 2 = 4 $$
همچنین داریم:
$$ \sigma _ { 1 2 } ^ 2 = \frac { \sigma _ 1 ^ 2 \sigma _ 2 ^ 2 }{ \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 } = 2 $$
$$ \mu _ { 1 2 } = \frac { \sigma _ 1 ^ 2 \mu _ 2 + \sigma _ 2 ^ 2 \mu _ 1 } { \sigma _ 1 ^ 2 + \sigma _ 2 ^ 2 } = 0 $$
این توزیعهای احتمالاتی را با استفاده از کد متلب زیر رسم میکنیم.
1clc;close all;clear all
2
3X = -10:0.01:10;
4mu1 = -4 ; sigma1 = 2;
5mu2 = 4 ; sigma2 = 2;
6
7mu12 = (sigma1^2*mu2 + sigma2^2*mu1)/(sigma1^2 + sigma2^2);
8sigma12 = sqrt((sigma1^2*sigma2^2)/(sigma1^2 + sigma2^2));
9
10display(['\mu_{12} = ' num2str(mu12) ', \sigma_{12} = ' num2str(sigma12)] )
11
12f1 = 1/sqrt(2*pi*sigma1^2) * exp( -(X-mu1).^2/(2*sigma1^2) );
13f2 = 1/sqrt(2*pi*sigma2^2) * exp( -(X-mu2).^2/(2*sigma2^2) );
14f12 = 1/sqrt(2*pi*sigma12^2) * exp( -(X-mu12).^2/(2*sigma12^2) );
15figure;
16plot(X,f12,X,f1,'g--',X,f2,'g--')
17axis([-10 10 0 .4])
18xlabel('X')
19ylabel('Probability distribution')نتیجه به صورت زیر خواهد بود.
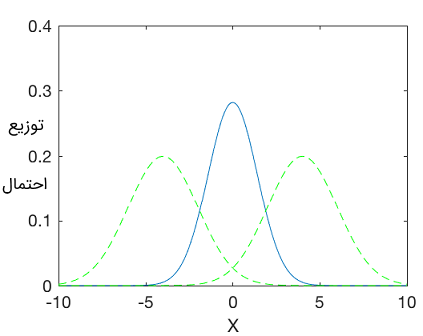
1\mu_{12} = 0, \sigma_{12} = 1.4142توزیع گاوسی دو بعدی
تکنیکهای تخمینی که تا کنون آنها را بررسی کردیم، فقط برای سیستمهای یک بعدی قابل استعمال هستند. به عبارت دیگر، برای مواردی که فقط یک متغیر نامعلوم وجود داشته باشد، میتوان از آنها استفاده کرد. اما برای مواردی که بیش از یک متغیر نامعلوم در سیستم داشته باشیم، باید از توزیعهای چند متغیره استفاده کنیم. ایده اساسی در پس یک توزیع چند متنغیره در تصویر زیر نشان داده شده است.
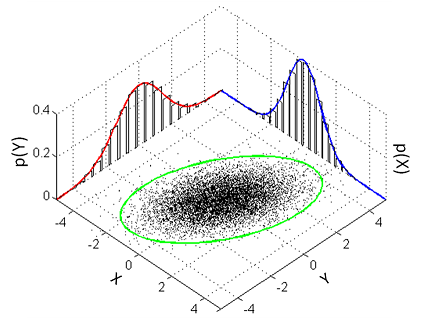
همان طور که از تصویر فوق مشخص است، یک توزیع چند متغیره متشکل از دو متغیر اصلی، توسط دو توزیع تک متغیره توصیف شده است که مرکز توزیع چند متغیره در محل میانگین آن دو توزیع تک متغیره قرار گرفته است. یک توزیع چند متغیره در K بعد به صورت زیر نشان داده خواهد شد:
$$ f ( X | \mathbf { \mu }, \mathbf { \Sigma } ) = \frac { 1 } { \sqrt { ( 2 \pi ) ^ k | \mathbf { \Sigma } | } } e ^ { - \frac { 1 } { 2 } ( X - \mathbf { \mu } ) ^ T \mathbf { \Sigma } ^ { - 1 } ( X -\mathbf { \mu } ) } $$
در رابطه فوق، $$ \Sigma $$ برابر با ماتریس کواریانس و $$ \mu $$ برابر با میانگین توزیع است. در حالت خاصی که $$ K = 2 $$ باشد، میتوان نوشت:
$$ \mathbf { \Sigma } = \left [ \begin {array} { c c } \sigma _ X ^ 2 & \sigma _ { X , Y } \\
\sigma _ { X, Y } & \sigma _ Y ^ 2 \end {array} \right] $$
در رابطه فوق، $$ \sigma _ { X , Y} $$ برابر با «گشتاور دوم» (Second Moment) بین متغیرهای X و Y است.
فیلتر کالمن دو بعدی در کنترل عدم قطعیت
تکنیکی در بخش قبل به معرفی آن پرداختیم در ترکیب با اطلاعات دینامیکی سیستم منجر به تشکیل فیلتر کالمن میشود. فیلترهای کالمن تخمین حالت را در دو گام اساسی انجام میدهند. گام اول شامل انتشار دینامیکهای سیستم است تا با استفاده از آن «احتمال پیشین» (Apriori Probability) حالتهای سیستم را به دست آورد. زمانی که اندازهگیریها انجام شدند، متغیرهای حالت با استفاده از قضیه بیز محاسبه و آپدیت میشوند. این مفهوم با مثالی در ادامه روشنتر خواهد شد.
موردی را در نظر بگیرید که خودرویی در امتداد یک مسیر مستقیم با سرعت ثابت در حال حرکت است. فرض کنید فقط اندازهگیریهای موقعیت (نه سرعت) را در اختیار دشته باشیم. در ابتدا، موقعیت را با استفاده از سنسور به دست میآوریم. بنابراین ناحیهای که حالتهای ربات میتوانند در آن قرار داشته باشند، مطابق با تصویر زیر خواهد بود.
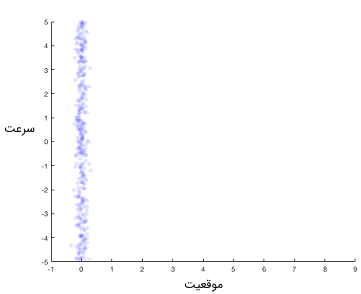
اگر ربات در همین موقعیت باقی بماند، آنگاه نمیتوان سرعت را تخمین زد. اما اگر ربات شروع به حرکت کند، آنگاه توزیع احتمالاتی موقعیت بعد از یک ثانیه حرکت با سرعت ثابت با ابری قرمز رنگ در تصویر زیر نشان داده شده است.
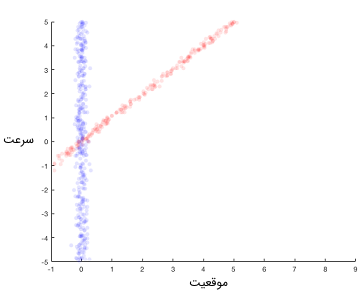
فرض کنید ربات با سرعت ثابت ۱ حرکت کند، تخمین موقعیت بعدی در حدود ۱ است. با انجام اندازهگیری دوم در این نقطه، ناحیه آبی رنگ در تصویر زیر را به عنوان مقادیر مثبت برای تخمین موقعیت خواهیم داشت.
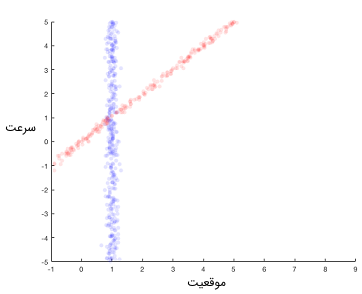
بنابراین با استفاده از دینامیکهای سیستم، انتظار داریم که موقعیت جدید در ناحیه قرمز رنگ باشد، اما با استفاده از دادههای سنسور، موقعیت خودرو باید در ناحیه آبی رنگ قرار داشته باشد. ناحیه همپوشانی بین این دو منطقه بسیار کوچک است و تئوری بیز را میتوان برای تخمین احتمال توزیع حالتهای چندگانه به کار برد. توزیع احتمالاتی متناظر با سرعت و موقعیت در طول دو محور X و Y در تصویر زیر نشان داده شده است.
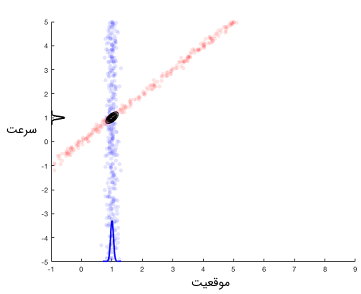
این فرایند ترکیب دینامیکهای سیستم با اندازهگیریهای سنسورها سنگ بنای اساسی فیلترهای کالمن است. فیلترهای کالمن دارای مشخصه تخمین بسیار خوبی هستند و در مواقعی که فرایند و اندازهگیری منطبق بر توزیع گاوسی باشند، انتخابی بهینه محسوب میشوند.
بهینگی (Optimality) در فیلتر کالمن
همان طور که گفتیم، فیلتر کالمن اطلاعات دینامیک سیستم را با اندازهگیریهای سنسورها ترکیب میکند و در نتیجه تخمین بسیار بهتری را از حالتهای سیستم فراهم میکند. اما تا این قسمت هنوز به نحوه ترکیب اطلاعات دینامیک سیستم و دادههای اندازهگیری سنسور نپرداختیم. برای بررسی این موضوع، یک فرایند بهینه سازی را انجام میدهیم که احتمال تعلق گرفتن حالتها به یک ناحیه را بیشینه میکند. به این روش، «تخمین حداکثر درستنمایی» (Maximum Likelhood Estimate) میگویند.
تخمین حداکثر درستنمایی: مثال رگرسیون خطی
درستنمایی این که یک مقدار متعلق به یک توزیع مفروض باشد را میتوان با توجه به تابع چگالی احتمال محاسبه کرد. بنابراین در حالت خاصی که توزیع نرمال باشد، درستنمایی مشاهده مقدار X توسط رابطه زیر به دست میآید:
$$ p ( X | \mu , \sigma ^ 2 ) = \frac { 1 } { \sqrt { 2 \pi \sigma ^ 2 } } e ^ { - \frac { ( X - \mu ) ^ 2 } { 2 \sigma ^ 2 } } $$
حال هدف مورد نظر ما این است که مقدار $$ \beta _ 0 $$ و $$ \beta _ 1 $$ را به نحوی تعیین کنیم که منجر به بیشینه شدن احتمال مقدار داده شده $$ y $$ به فرم $$ \beta _ 0 + \beta _ 1 X $$ شود. به عبارت دیگر، هدف تخمین پارامترهای $$ \beta _ 0 $$ و $$ \beta _ 1 $$ است تا احتمال خطایی که از تقریب خطی حالتها ناشی میشود، بیشینه شود. به علاوه، فرض میکنیم که خطاها دارای توزیع نرمال و «میانگین امید صفر» (Zero Expected Mean) باشند. آنگاه احتمال مشاهده یک خطا به اندازه $$ e _ i = y _ i - ( \beta _ 0+ \beta _ 1 x _ i ) $$ به صورت زیر به دست میآید:
$$ p ( e _ i | 0 , \sigma ^ 2 ) = \frac { 1 } { \sqrt { 2 \pi \sigma ^ 2 } } e ^ { - \frac { ( y _ i - ( \beta _ 0 + \beta _ 1 x _ i ) ) ^ 2 } { 2 \sigma ^ 2 } } $$
در نتیجه احتمال مشاهده خطاهای $$ e _ 1 $$ و $$ e _ 2 $$ تا $$ e _ N $$ برابر است با:
$$ p ( e _ 1, e _ 2, \dots , e _ N ) = \underbrace { \Pi } _ { i = 1 ~ t o ~ n } p ( e _ i | 0, \sigma ^ 2 ) $$
نماد $$ \Pi $$ نشان دهنده ضرب بین احتمالات است. حال میتوان نوشت:
$$ \large p ( e _ 1, e _ 2, \dots , e _ N ) = \underbrace { \Pi } _ { i = 1 ~ t o ~ n } p ( e _ i | 0, \sigma ^ 2 ) = \underbrace { \Pi } _ { i = 1 ~ t o ~ n } \frac { 1 } { \sqrt { 2 \pi \sigma ^ 2 } } e ^ { - \frac { ( y _ i - ( \beta _ 0 + \beta _ 1 x _ i ) ) ^ 2 } { 2 \sigma ^ 2 } } $$
بنابراین هدف فرایند بهینهسازی این است که پارامترها برای بیشینه کردن تابع احتمالی را به دست آورد. به دلیل این که پارامترهای $$ \beta _ 0 $$ و $$ \beta _ 1 $$ فقط در توان ظاهر میشوند، در نتیجه میتوانیم از تابع احتمال لگاریتم بگیریم:
$$ \underbrace { Maximize } _ { \beta _ 0 , \beta _ 1 } ~ log ( p ( e _ 1 , e _ 2, \dots , e _ N ) ) = \underbrace { Maximize } _ { \beta _0 , \beta _ 1 } \sum _ { i = 1 } ^ N \left (- \frac { ( y _ i - ( \beta _ 0 + \beta _ 1 x _ i ) ) ^ 2 } { 2 \sigma ^ 2 } - \frac { 1 } { 2 } log ( 2 \pi \sigma ^ 2 ) \right ) $$
عبارات فوق را «احتمال لگاریتم بیشینه» (Maximum Log Likelihood) نیز میگویند. به دلیل این که ما منفی یک مقدار را بیشینه میکنیم و نیز به این دلیل که با یک عدد ثابت جمع و ضرب میکنیم، در نتیجه مسئله احتمال بیشینه را میتوان به صورت زیر نیز بیان کرد:
$$ \underbrace { Minimize } _ { \beta _ 0 , \beta _ 1 } \sum _ { i = 1 } ^ N \left ( y _ i - ( \beta _ 0 + \beta _ 1 x _ i ) \right ) ^ 2 $$
توجه کنید که عبارت $$ \frac { 1 } { 2 } log ( 2 \pi \sigma ^ 2 ) $$ یک مقدار ثابت است و به همین دلیل در بیشینه کردن عبارت کلی هیچ تاثیری نخواهد داشت و به همین دلیل میتوان از آن صرف نظر کرد. با دقت در رابطه به دست آمده در بالا میتوان به این نتیجه رسید که تابع حداکثر احتمال به یک مسئله یافتن خط برازش حداقل مربعات تبدیل شده است. روندی مشابه را میتوان برای تخمین حالتها در فیلتر کالمن نیز به کار گرفت.
فیلتر ذرهای (Particle Filters) در کنترل عدم قطعیت
فیلترهای ذرهای، بر خلاف فیلترهای مبتنی بر مدل، کلاسی از فیلترهای مبتنی بر شبیهسازی هستند. در مورد این سنسورها هیچ فرضی درباره مدل پلنت مورد نظر انجام نخواهیم داد. ایده اولیه این است که برای تمام مقادیر ممکن حالتها از فضا نمونهبرداری کنیم و سپس به هر نقطه یک وزن اختصاص بدهیم که به این بستگی داشته باشد که تا چه حد اندازهگیری به نقطه واقعی نزدیک باشد. زمانی که وزنها به دست آمد، آنگاه حالتهای پلنت با احتمال بقا هر ذره که متناسب با وزن آن است، باز نمونه برداری میشوند.
در طول زمان، نقاطی که اندازهگیری آنها متناسب با حالتهای بسیار نامحتمل هستند، حذف میشوند و نقاطی که محتملتر هستند، حفظ خواهند شد. وزنها معمولا به صورت توزیع گاوسی چند متغیره انتخاب میشوند. «باز نمونهگیری» (Resampling) را میتوان به صورت واضحتر توسط یک گردونه چرخان رولتی توضیح داد که در آن تغیر بقای هر ذره بر اساس بزرگی ناحیهای تعیین میشود که اشغال کرده است. نمایی از یک گردونه چرخان نشان داده شده است.
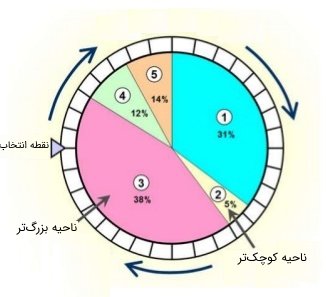
در گردونه تصویر فوق، اجزای متناسبتر دارای سهم بزرگ تری از صفحه گردان هستند و اجزای ضعیفتر، سهم کوچکتری از گردونه را به خود اختصاص دادهاند.
انیمیشن زیر یک پیادهسازی از فیلتر ذرهای مربوط به یک SLAM دو بعدی را در دو حالت نویز بالا و نویز پایین نشان میدهد.
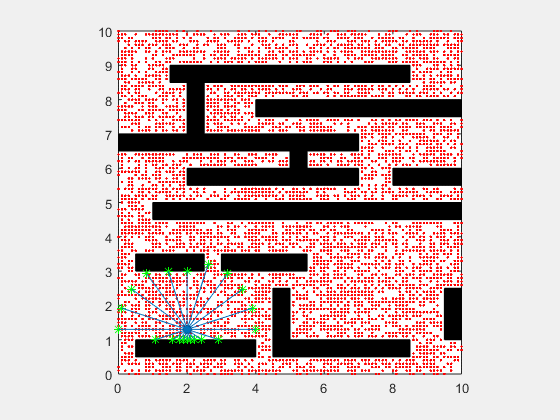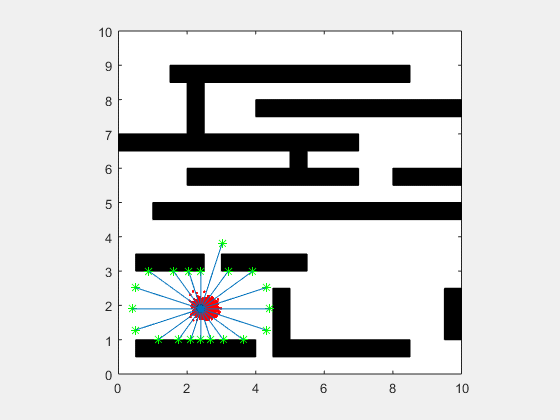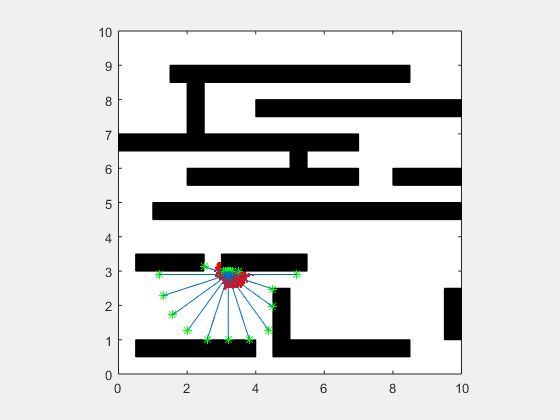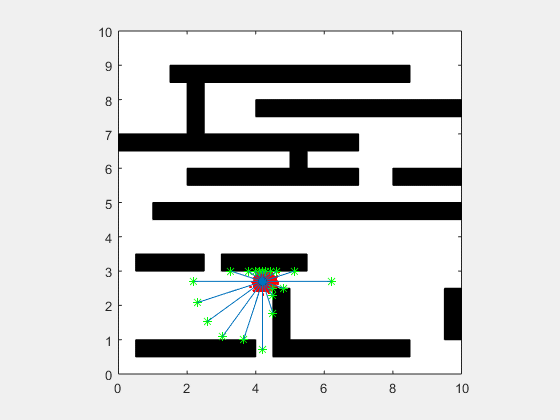
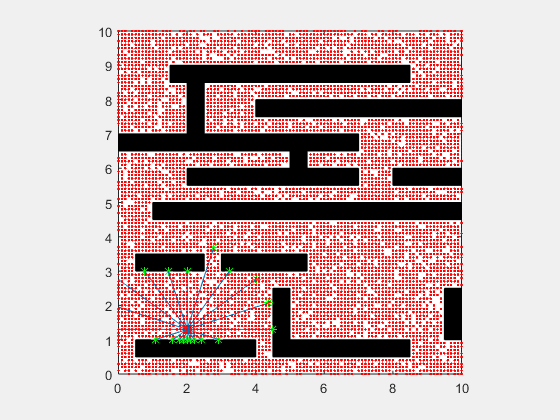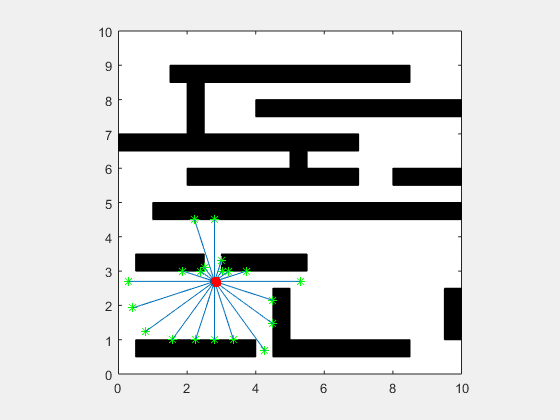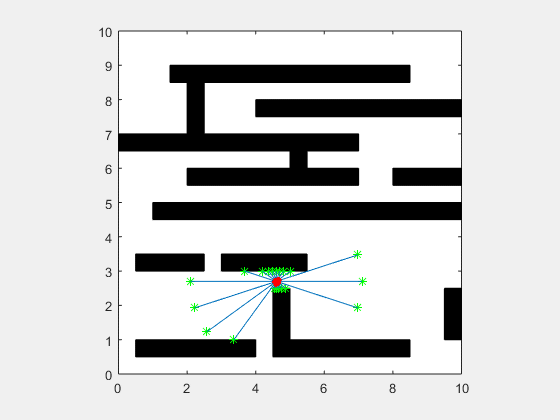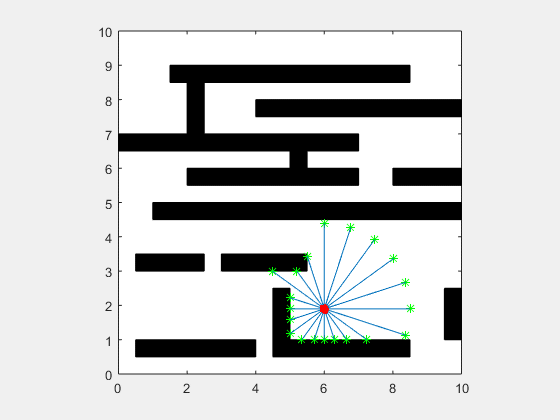
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی کنترل
- آموزش کنترل بهینه
- مجموعه آموزشهای مهندسی برق
- آموزش کاربرد متلب در مهندسی کنترل
- سیستم غیر خطی — راهنمای جامع
- کنترل بهینه در متلب — از صفر تا صد
- کنترل پیش بین مدل (MPC) — راهنمای جامع
^^











مثال ۲: احتمال ترکیبی گاوسی اشتباه چابی دارد برای مقدار میانگینُ لطفا کنترل مجدد بفرمایید
سلام.
متن اصلاح شد.
سپاس از همراهی و بازخوردتان.
خیلی خوب بود. ممنون