محاسبه کوواریانس و ضریب همبستگی در اکسل – به زبان ساده


زمانی که از دو متغیر یا بیشتر در تحلیلهای آماری استفاده میکنید، لازم است که میزان وابستگی یا ارتباط بین متغیرها را اندازهگیری و در تحلیلها لحاظ کنید. یکی از روشهای اندازهگیری میزان وابستگی یا ارتباط بین متغیرها، محاسبه کوواریانس و ضریب همبستگی است. در این نوشتار به بررسی نحوه محاسبه این دو شاخص در اکسل میپردازیم. این کار در دو قسمت صورت میگیرد. ابتدا به بررسی نحوه محاسبه بدون استفاده از توابع اکسل پرداخته تا مفهوم این دو بیشتر مشخص شود سپس با کمک گرفتن از توابع اکسل و ابزارهای کمکی کوواریانس و ضریب همبستگی را محاسبه میکنیم.
برای آشنایی بیشتر با مفهوم کوواریانس بهتر است ابتدا نوشتار امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و به منظور آگاهی از نحوه محاسبه انواع ضریب همبستگی نیز مطلب ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده را بخوانید. البته خواندن نوشتار واریانس و اندازههای پراکندگی — به زبان ساده و محاسبه واریانس در اکسل — به زبان ساده نیز خالی از لطف نیست.
محاسبه کوواریانس و ضریب همبستگی
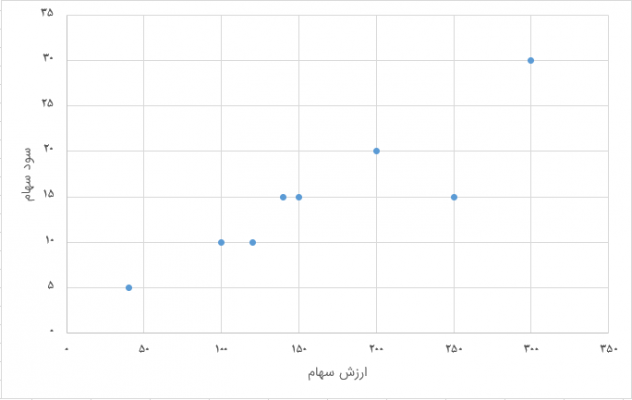
معمولا از دو شیوه یا روش برای اندازهگیری میزان ارتباط بین دو متغیر یا دو سری داده استفاده میشود. محاسبه کوواریانس یکی از این شاخصها و روشها است. برای مثال اگر به نمودارهای زیر توجه کنید، ارتباط بین دو متغیر که یکی روی محور افقی و دیگری در محور عمودی ظاهر شده، به خوبی وجود رابطه را نشان میدهد.
مشخص است که در تصویر شماره ۱ با افزایش یکی، دیگری نیز افزایش یافته است. به چنین حالتی، رابطه مستقیم میگویند.
همچنین در نموداری که در تصویر شماره ۲ دیده میشود، وجود رابطه معکوس بین دو متغیر مشخص است به این معنی که با افزایش یکی، دیگری کاهش مییابد.
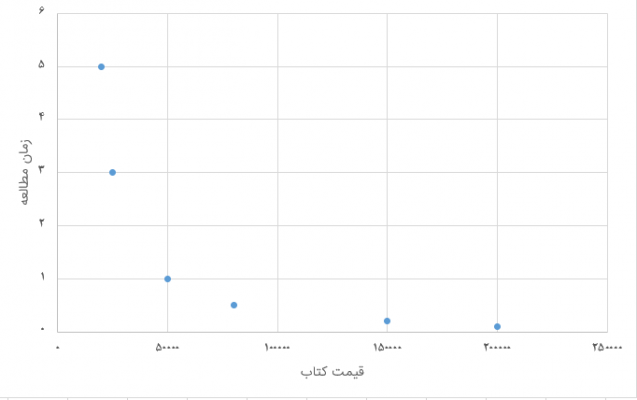
کوواریانس به واحد اندازهگیری دو متغیر حساس است. اگر بخواهیم حساسیت به مقیاس را از بین ببریم، محاسبه ضریب همبستگی اهمیت پیدا میکند. در ادامه متن ابتدا به معرفی کوواریانس پرداخته، سپس شیوه محاسبه ضریب همبستگی را معرفی میکنیم.
محاسبه کوواریانس
«کوواریانس» (Covariance)، شاخصی است که میزان هماهنگی یا تغییرات بین دو متغیر را نشان میدهد. اگر جهت تغییرات بین دو متغیر یکسان باشد مقدار کوواریانس مثبت و در صورتی که دو متغیر در جهت عکس یکدیگر تغییر کنند، مقدار کوواریانس منفی خواهد بود. به این ترتیب اگر با افزایش متغیر متغیر نیز افزایش یابد، کوواریانس و البته «ضریب همبستگی» (Correlation Coefficient) مثبت خواهد بود. همین توضیح را در زمانی که کاهش متغیر منجر به کاهش متغیر نیز شود میتوان به کار برد. در هر دو صورت، کوواریانس و ضریب همبستگی مثبت هستند زیرا جهت تغییرات دو متغیر یکسان است.
برای مثال، فرض کنید میزان ارزش سهام یک شرکت و سود سهامداران دارای رابطه مستقیم است در نتیجه کوواریانس مثبت خواهد بود. به این معنی که با افزایش یا کاهش یکی، دیگری هم به همان ترتیب افزایش یا کاهش خواهد داشت. بزرگی کوواریانس و ضریب همبستگی نشان دهنده شدت رابطه بین دو متغیر نیز هست. به این معنی که اگر کوواریانس بین ارزش سهام و سود سهامداران در بین دو شرکت به ترتیب برابر با ۱۰۰+ و ۱۵+ باشد، به نظر میرسد که سرمایهگذاری در شرکت دوم به صرفهتر است.
ولی اگر با افزایش یکی دیگری کاهش یابد، کوواریانس منفی است تا نشان دهد که جهت تغییرات دو متغیر عکس یکدیگر است. برای مثال اگر افزایش یابد، همزمان نیز کاهش یابد، کوواریانس و ضریب همبستگی منفی شده و بیانگر تغییرات دو متغیر در جهت عکس یکدیگر است. برای مثال میتوان میزان ساعات مطالعه کتاب و قیمت کتاب در کشور را در نظر گرفت. هر چه قیمت کتاب افزایش یابد ساعت مطالعه کاهش خواهد یافت و برعکس با کاهش قیمت کتاب، ساعات مطالعه در کشور افزایشی خواهد بود. بنابراین اگر در مقایسه سال ۱۳۹۷ و ۱۳۹۸، کوواریانس این دو متغیر به ترتیب ۱۲۰- و ۵۰۰- باشد، نشان میدهد که در سال ۱۳۹۸ افزایش قیمت کتاب، کاهش زمان مطالعه بیشتری را نسبت به سال ۱۳۹۷ رقم زده است.
مثال ۱
محاسبه کوواریانس بسیار ساده است. با استفاده از دادههای ارائه شده در جدول زیر با نحوه اندازهگیری کوواریانس آشنا میشویم. این دادهها مربوط به ارزش سهام و سود 8 شرکت بورسی در سال ۱۳۹۷ است.
| نام شرکت | الف | ب | پ | ت | ث | ج | چ | ح |
| ارزش سهام (تومان) | ۲۰۰ | ۲۵۰ | ۳۰۰ | ۱۲۰ | ۱۴۰ | ۴۰ | ۱۰۰ | ۱۵۰ |
| سود سهام (تومان) | 20 | 15 | 30 | 10 | 15 | 5 | 10 | 15 |
فرض کنید ارزش سهام را با و سود سهام را با نشان دهیم. فرمول محاسباتی برای کوواریانس بین و به شکل زیر محاسبه میشود.
فرمول ۱
مشخص است که و میانگین و را نشان میدهند.
نکته: با توجه به فرمول ارائه شده به نظر میرسد که کوواریانس خاصیت تقارن دارد. به این معنی که . پس اگر کوواریانس با را محاسبه کردهایم دیگر احتیاجی به محاسبه کوواریانس با نیست.
حال براساس اطلاعات جدول بالا، محاسبات را طبق فرمول ۱، انجام داده و در جدولی به مانند زیر بازنویسی میکنیم.
| نام شرکت | |||||
| الف | 200 | 200-162.5=37.5 | 20 | 20-15=5 | 37.5 ×5=187.5 |
| ب | 250 | 250-162.5=87.5 | 15 | 15-15=0 | 87.5 ×0= 0 |
| پ | 300 | 137.5 | 30 | 15 | 2062.5 |
| ت | 120 | -42.5 | 10 | -5 | 212.5 |
| ث | 140 | -22.5 | 15 | 0 | 0 |
| ج | 40 | -122.5 | 5 | -10 | 1225 |
| چ | 100 | -62.5 | 10 | -5 | 312.5 |
| ح | 150 | -12.5 | 15 | 0 | 0 |
| جمع | 1300 | 120 | |||
| میانگین | 162.5 | 15 | 500 |
از آنجایی که مقدار کوواریانس مثبت است نشان میدهد که وابستگی یا ارتباط بین دو متغیر ارزش سهام و سود سهامداران در یک راستا است.
نکته: از آنجایی که هر یک از متغیرها با واحد تومان اندازهگیری شدهاند، واحد اندازهگیری کوواریانس در اینجا به صورت تومان مربع (تومان به توان ۲) است زیرا بواسطه ضرب دو مقدار برحسب تومان محاسبه شده است. بنابراین اگر هنگام محاسبه کوواریانس، یک متغیر برحسب کیلوگرم و متغیر دوم برحسب متر اندازهگیری شده باشند، کوواریانس آنها برحسب «کیلوگرم در متر» خواهد بود.
میتوان محاسبه کوواریانس را به شکل سادهتری نیز انجام داد. کافی است که فرمول ارائه شده در قسمت قبل را کمی باز کنیم. در ضمن از این به بعد کوواریانس بین دو متغیر و را با نشان خواهیم داد.
بنابراین شیوه سادهتر برای محاسبه کوواریانس در فرمول ۲ دیده میشود.
مشخص است که در اینجا منظور از میانگین حاصلضرب دو متغیر است. به این ترتیب جدول بالا را به صورت زیر بازنویسی میکنیم تا مقدارهای مورد نظر برای محاسبه کوواریانس بدست آیند.
| نام شرکت | |||
| الف | 200 | 20 | 4000 |
| ب | 250 | 15 | 3750 |
| پ | 300 | 30 | 9000 |
| ت | 120 | 10 | 1200 |
| ث | 140 | 15 | 2100 |
| ج | 40 | 5 | 200 |
| چ | 100 | 10 | 1000 |
| ح | 150 | 15 | 2250 |
| جمع | 1300 | 120 | 23500 |
| میانگین | 162.5 | 15 | 2937.5 |
همانطور که مشخص است، برای محاسبه کوواریانس کافی است که میانگین حاصل ضربها را از حاصلضرب میانگینها کم کنیم. یعنی:
نکته: با توجه به نحوه محاسبه کوواریانس در فرمول ۱ یا فرمول ۲، مشخص است که اگر مقدارهای ارزش سهام و سود سهام را برحسب ریال تنظیم میکردیم، مقدار کوواریانس ۱۰ برابر میشد. بنابراین اگر میخواهیم کوواریانس یا میزان رابطه بین ارزش سهام و سود سهام را در بین این دو شرکت برای سال ۱۳۹۷ و ۱۳۹۸ مقایسه کنیم، حتما باید از یک واحد پولی (مثلا تومان) استفاده کرده تا انجام مقایسه صحیح باشد. در غیر اینصورت اگر مقیاس اندازهگیری در سال ۱۳۹۷ برحسب تومان و در سال ۱۳۹۸ برحسب ریال باشد، ممکن است تفسیر مناسبی از این موضوع حاصل نشده و به نظر برسد که در سال ۱۳۹۸ میزان ارتباط بین دو متغیر ۱۰ برابر سال ۱۳۹۷ است.
محاسبه کوواریانس در اکسل
در ادامه سعی میکنیم که محاسبه کوواریانس را در محیط اکسل برای دادههای مثال قبل اجرا کنیم. در تصویر زیر دادههای وارد شده و انواع توابع محاسباتی برای کوواریانس دیده میشود.

همانطور که میبینید سه تابع به نامهای COVARIACEN.P, COVARIANCE.S, COVAR برای محاسبه کوواریانس در اکسل وجود دارند. هر چند پارامترهای این توابع دقیقا یکی هستند ولی شیوه محاسبه آنها کمی متفاوت است.
تابع COVARIANCE.P ،COVARIANCE.S و COVAR
این سه تابع مطابق با فرمول ۱ یا مترادف آن یعنی فرمول ۲، محاسبه کوواریانس را انجام میدهند. با این تفاوت که توابع COVARIANCE.P و COVAR که به «کوواریانس جامعه آماری» (Population Covariance) معروف هستند مقدار را همان تعداد مشاهدات در نظر میگیرند ولی در شیوه محاسبه COVARIANCE.S که به «کوواریانس نمونهای» (Sample Covariance) معروف است، مقدار یکی کمتر از تعداد مشاهدات در فرمولهای یاد شده است.
پارامترهای مربوط به این توابع به صورت زیر است.
COVARIANCE.P(array1,array2)
COVARIANCE.S(array1,array2)
COVAR(array1,array2)
منظور از array1 همان و array2 نیز در فرمولهای گفته شده است که میتوانند یک بردار شامل مجموعهای از مقدارها یا آدرس ناحیهای از کاربرگ اکسل باشند. باید دقت کنید که اندازه این بردارها باید دقیقا یکسان باشند به این معنی که اگر array1 شامل ناحیهای با ۱۰ سلول است، باید array2 نیز ناحیهای با ۱۰ سلول را مشخص کند. در غیر اینصورت در سلول مورد نظر با خطای $$#VALUE!$$
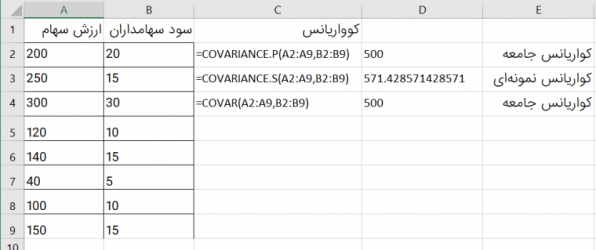
همانطور که مشاهده میکنید مقدار محاسبه شده کوواریانس نمونهای بزرگتر از کوواریانس جامعه آماری است زیرا مخرج کسر مربوط به فرمول ۱ کوچکتر است.
نکته: تابع COVAR مربوط به نسخههای قدیمی اکسل است و فقط به منظور سازگاری در نسخههای جدیدتر اکسل قرار گرفته است. بهتر است در کاربرگهایی که ایجاد می کنید از این تابع استفاده نکنید زیرا ممکن است در نسخههای آینده اکسل از این تابع پشتیبانی نشود.
برای دسترسی به این توابع میتوانید از برگه Formula، دکمه More Functions را انتخاب کرده و از گروه Statistical تابعهای COVARIANCE.P یا COVARIANCE.S را انتخاب و پارامترهای آن را مطابق با پنجره زیر تعیین کنید.
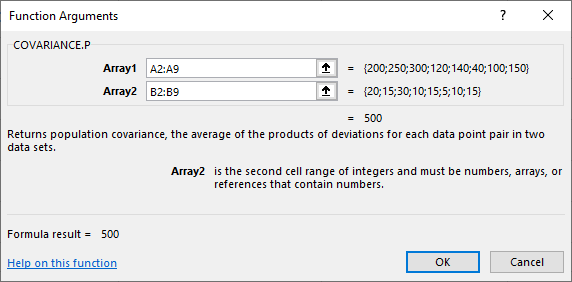
به منظور درج تابع COVAR باید از برگه Formula دکمه More Functions و گروه Compatibility را انتخاب و تابع COVAR را از درون لیست پیدا کنید. پنجره تعیین پارامترهای این تابع درست به مانند تصویر قبل است. پنجره Function Arguments یا پنجره پارامترهای تابع دو کادر به عنوان پارامترها توابع محاسبه کوواریانس به نامهای Array1 و Array2 را نشان میدهد. اگر میخواهید اکسل راهنمای استفاده از این تابع را ظاهر کند، کافی است که روی لینک Help on this Function کلیک کنید. با فشردن دکمه OK (یا کلید Enter از صفحه کلید) محاسبه انجام شده و در سلول مورد نظر قرار میگیرد. ولی با زدن دکمه Cancel اعلام میکنید که از ثبت تابع در سلول صرفنظر کردهاید و به کاربرگ اطلاعاتی بازخواهید گشت.
محاسبه ضریب همبستگی
همانطور که گفته شد ممکن است در تفسیر کوواریانس دچار مشکل شویم زیرا مقدار کووریانس تحت تاثیر واحدهای اندازهگیری متغیرهای و قرار دارد. برای رفع این مشکل و استاندارد کردن مقدار وابستگی بین دو متغیر، از ضریب همبستگی استفاده میشود. به همان شکل که مثبت و منفی بودن کوواریانس، جهت ارتباط و وابستگی بین دو متغیر را تعیین میکرد، علامت ضریب همبستگی نیز جهت وابستگی بین دو متغیر را مشخص میکند.
اگر ضریب همبستگی مثبت باشد، هر دو متغیر هم جهت تغییر میکنند و اگر ضریب همبستگی منفی باشد، تغییرات دو متغیر عکس یکدیگر است.
نحوه محاسبه ضریب همبستگی بین دو متغیر و مطابق با فرمول ۳ است. معمولا ضریب همبستگی را با علامت یا Corr نشان میدهند.
فرمول ۳
مشخص است که در مخرج کسر، منظور از ، انحراف معیار (جذر واریانس) متغیر است. همچنین نیز انحراف معیار متغیر را نشان میدهد. در صورت کسر نیز همان کوواریانس بین دو متغیر محاسبه شده است. از آنجایی که صورت (کوواریانس) و حاصل ضرب انحراف معیارها هم واحد هستند، نسبتشان بدون واحد خواهد بود. این شیوه اندازهگیری ضریب همبستگی به نام «ضریب همبستگی پیرسون» (Pearson Correlation Coefficient) معروف است.
به این ترتیب اگر یک متغیر برحسب کیلوگرم و متغیر دوم برحسب متر باشد، مقدار ضریب همبستگی بدون واحد بیان خواهد شد. به همین علت برای مقایسه شدت رابطه برای دو متغیر در وضعیتهای مختلف ضریب همبستگی بسیار مناسب است. برای مثال ممکن است بخواهیم شدت رابطه بین ارزش سهام و سود سهامداران را در دو سال مختلف با هم مقایسه کنیم. در سال اول این متغیرها برحسب تومان اندازهگیری شدهاند. در سال دوم این متغیرها برحسب ریال معرفی شدهاند. برای آنکه بتوانیم با حذف واحد اندازهگیری شدت رابطه بین دو متغیر را در این دو سال مقایسه کنیم، ضریب همبستگی را به کار میبریم.
به منظور یادآوری، فرمول محاسبه واریانس جامعه و واریانس نمونه، برای متغیر را در ادامه مشاهده میکنید.
واریانس جامعه:
واریانس نمونه:
مقدار ضریب همبستگی در فاصله تغییر میکند. هر چه مقدار ضریب همبستگی به ۱ یا 1- نزدیکتر باشد، میزان رابطه خطی بین دو متغیر شدیدتر است. اگر ضریب همبستگی به صفر نزدیک باشد، رابطه خطی بین دو متغیر ضعیف در نظر گرفته میشود. البته هنگامی که ضریب همبستگی به ۱+ نزدیک باشد، رابطه شدید خطی و از نوع مستقیم و در یک جهت است. در صورتی که ضریب همبستگی به ۱- نزدیک باشد، رابطه خطی بین دو متغیر به صورت معکوس است.
نکته: از آنجایی که ضریب همبستگی برحسب کوواریانس محاسبه میشود، خاصیت تقارن را هم خواهد داشت. بنابراین ضریب همبستگی بین و با ضریب همبستگی با برابر است.
مثال 2
براساس دادههای مربوط به مثال ۱، ضریب همبستگی را محاسبه میکنیم. از آنجایی که کوواریانس برابر با ۵۰۰ شده است، فقط کافی است که انحراف معیار را برای هر دو متغیر بدست آوریم. از آنجایی که محاسبه انحراف معیار به کمک واریانس صورت میگیرد، ابتدا واریانس را مطابق با روشی که در مطلب واریانس و اندازههای پراکندگی — به زبان ساده یا محاسبه واریانس در اکسل — به زبان ساده بیان شده است، بدست میآوریم. محاسبات مربوط به واریانس و سپس انحراف معیار در جدول زیر صورت گرفته است.
| نام شرکت | ||||||
| الف | 200 | 37.5 | 1406.25 | 20 | 5 | 25 |
| ب | 250 | 87.5 | 7656.25 | 15 | 0 | 0 |
| پ | 300 | 137.5 | 18906.25 | 30 | 15 | 225 |
| ت | 120 | -42.5 | 1806.25 | 10 | -5 | 25 |
| ث | 140 | -22.5 | 506.25 | 15 | 0 | 0 |
| ج | 40 | -122.5 | 15006.25 | 5 | -10 | 100 |
| چ | 100 | -62.5 | 3906.25 | 15 | 0 | 25 |
| ح | 150 | -12.5 | 156.25 | 15 | 0 | 0 |
| میانگین | 162.5 | 6168.75 | 15 | 50 |
به این ترتیب واریانس جامعه آماری برای متغیر برابر با 6168.75 و برای متغیر نیز 50 است. اگر از هر یک از این مقدارها جذر گرفته شود، انحراف معیار بدست میآید که به ترتیب برابر با و خواهد بود. با جایگذاری در فرمول ۳ نتیجه ضریب همبستگی بین دو متغیر و حاصل میشود.
نکته: اگر به جای استفاده از کوواریانس جامعه آماری از کوواریانس نمونهای و به جای استفاده از واریانسها جامعه از واریانس نمونهای استفاده کنیم، ضریب همبستگی تغییری نخواهد کرد. به رابطه زیر دقت کنید.
با ساده کردن عبارت در صورت و مخرج کسر، رابطه به شکل زیر در خواهد آمد. که شامل عبارت نیست. به همین علت ضریب همبستگی در اکسل برای جامعه و نمونه تابع مجزایی ندارد.
محاسبه ضریب همبستگی در اکسل
برای محاسبه ضریب همبستگی در اکسل از دو تابع میتوان استفاده کرد. توابع CORELL و PEARSON هر دو محاسبه ضریب همبستگی را به عهده دارند، البته تابع CORREL نسبت به روش قبلی محاسبه ضریب همبستگی که در تابع PEARSON به کار رفته، دقیقتر و بخصوص برای اعداد بسیار بزرگ مناسب است. برای دسترسی به این دو تابع باز هم از برگه Formula دکمه More Functions را انتخاب کرده و از گروه Statistical تابعهای CORELL یا PEARSON را انتخاب و پارامترهای آنها را مطابق با پنجره زیر تعیین کنید.
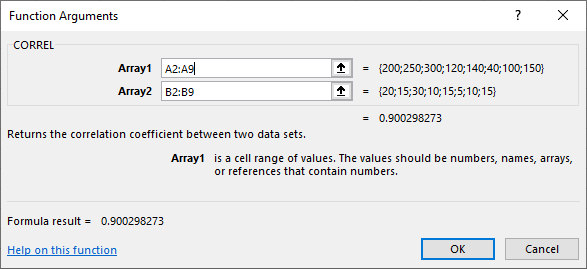
برای دادههای مربوط به مثال ۱ ضریب همبستگی را محاسبه کردهایم. همانطور که در پایین پنجره پارامترهای این تابع مشاهده میکنید، ضریب همبستگی تقریبا برابر با 0.9 است که بیانگر شدت زیاد و مستقیم رابطه بین دو متغیر ارزش سهام و سود سهامداران است. البته همین نتایج را با استفاده از تابع PEARSON نیز بدست خواهید آورد. ولی باید توجه داشت که در نسخههای قدیمی اکسل تابع PEARSON هنگام «گِرد کردن» (Round) اعداد یک خطای محاسباتی مرتکب میشد که در نسخههای بعدی رفع شده ولی بهتر است به هر حال از تابع CORREL برای محاسبه ضریب همبستگی استفاده کنید.
نکته: اگر بردارهایی که در پارامترهای Array1 و Array2 معرفی میکنید، هم اندازه نباشند در سلول پیغام خطای $$#N/A$$
محاسبه ماتریس کوواریانس و ماتریس ضریب همبستگی (بیش از دو متغیر)
همانطور که تا به اینجا خواندید، کوواریانس و ضریب همبستگی را بین دو متغیر محاسبه کردیم. اگر بیش از دو متغیر در اختیار داشته باشیم و بخواهیم کوواریانس یا ضریب همبستگی را برای ترکیبهای دو تایی از آنها ایجاد و محاسبه کنیم، باز هم میتوانیم از توابع گروه COVARIANCE یا CORREL استفاده کنید. به مثالی در این زمینه توجه کنید.
مثال ۳
فرض کنید متغیرهای تا متغیرهایی هستند که باید کوواریانس و ضریب همبستگی بین همه ترکیبات زوجهای آنها را محاسبه کنیم. مجموعه دادههایی این متغیرها در تصویر زیر دیده میشوند. با توجه به توابعی که کمی قبلتر برای محاسبه کوواریانس و ضریب همبستگی پیرسن در اکسل معرفی کردیم جدولی به صورت زیر ایجاد میکنیم. میخواهیم عناصر داخلی این جدول همان مقدار کوواریانس بین جفت متغیرها را نشان دهند. در تصویر زیر نحوه نوشتن این فرمولها مشخص شده است.
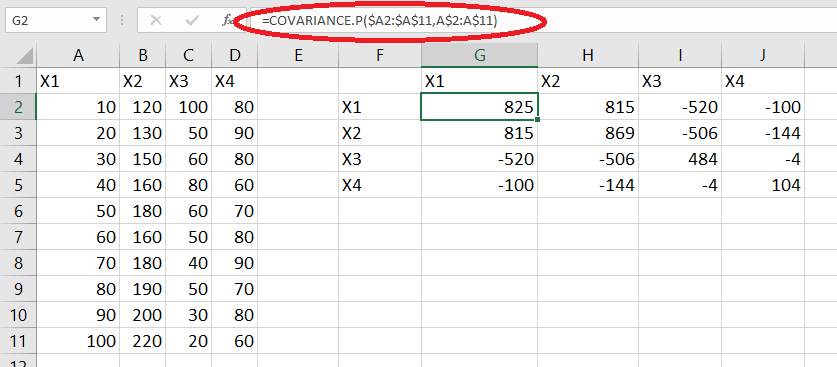
همانطور که در نوار فرمول دیده میشود، از آدرس ترکیبی سلولها در پارامتر اول به شکل $A$2:$A$11 و A$2:A$11 نوشته شده است. برای محاسبه کوواریانس برای سطرهای بعدی مثلا بین متغیر و باید فرمول را به شکل زیر بنویسید. برای مثال آدرس$$ $C$2 $$
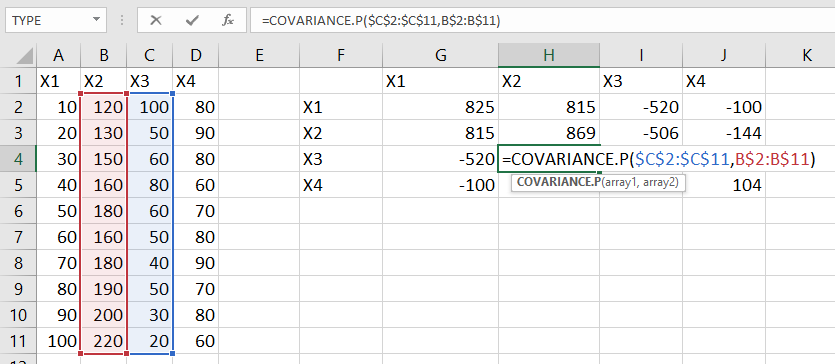
به همین ترتیب اگر لازم باشد که ضریب همبستگی را محاسبه کنیم، کافی است که به جای تابع COVARIANCE.P از CORREL استفاده شود.
نکته: اگر لازم است که کوواریانس نمونهای را محاسبه کنید، باید از تابع COVARIANCE.S در فرمولها استفاده کنید.
محاسبه کوواریانس و ضریب همبستگی با ابزارهای اکسل
بعضی از توابع و محاسبات در اکسل به واسطه ابزارهایی که در آن قرار دارد، صورت میگیرند. کوواریانس و ضریب همبستگی نیز توسط ابزار «تحلیل داده» (Data Analysis) محاسبه میشوند. البته با این ابزارها میتوانید ماتریس کوواریانس و ضریب همبستگی را برای بیش از دو متغیر نیز بدست آورید. برای ظاهر کردن دستور Data Analysis باید آن را در اکسل بارگذاری کنید. به این منظور روند زیر را طی کنید.
File -> Options -> Add-ins -> Excel Add-ins -> Go -> Analysis ToolPack
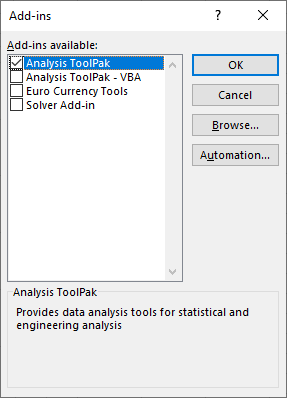
با انتخاب گزینه Analysis ToolPack و فشردن دکمه Ok در برگه Data گزینهای به نام Data Analysis ظاهر خواهد شد. حال کافی است که این دکمه را انتخاب کرده تا فهرستی از دستورات و ابزارهای تحلیلی اکسل ظاهر شود.
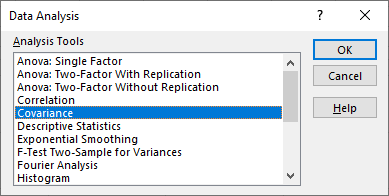
با انتخاب Covariance پنجره این ابزار ظاهر میشود. کافی است که پارامترهای صحیح را در این پنجره وارد کرده تا کوواریانس به صورت یک ماتریس بین چندین متغیر نمایش داده شود. فرض کنید دادهها مربوط به چهار متغیر به صورت زیر در کاربرگ اکسل ثبت شده باشند.
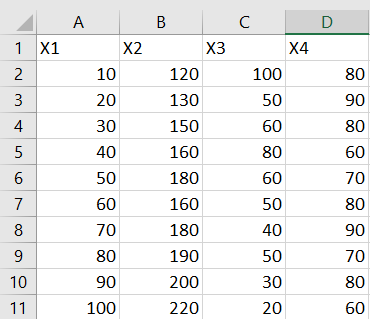
حال در پنجره ابزار کوواریانس تنظیمات را مطابق با تصویر زیر در میآوریم. مراحل و نقش هر یک از بخشهای مربوطه در ادامه مشخص میشوند.

در بخش ۱ که قسمت Input Range نامیده میشود ناحیه یا آدرس سلولهایی را مشخص میکنید که باید کوواریانس برای آنها محاسبه شود. در بخش شماره ۲ نیز نحوه برداشت متغیرها را در Input Range تعیین میکنید. اگر در قسمت Grouped By گزینه Columns را انتخاب کنید به این معنی است که باید کوواریانس بین ستونها محاسبه شود. در صورتی که Rows انتخاب شود، کوواریانس بین سطرها حاصل خواهد شد.
در بخش ۳، با انتخاب Labels in First Row به اکسل میگویید که سطر اول جدول معرفی شده در Input Range شامل اسامی متغیرها نیز هست و نباید از آن برای محاسبات استفاده شود. در قسمت انتهایی (Output options) یا بخش ۴ نیز محل ایجاد ماتریس کوواریانس را تعیین میکنید. گزینه Output Range به شما اجازه میدهد که سلولی را انتخاب کنید که محل ایجاد ماتریس کوواریانس باشد. گزینه New Worksheet Ply هم برای نمایش ماتریس کوواریانس از یک کاربرگ جدید بهره میبرد که میتوانید نام آن را نیز در کادر روبرو وارد کنید. همچنین اگر لازم است که نتیجه این محاسبات را در کارپوشه دیگری ظاهر کنید، گزینه New Workbook، انتخاب مناسبی است. خروجی با توجه به تنظیمات انجام شده در تصویر قبلی به شکل زیر خواهد بود.
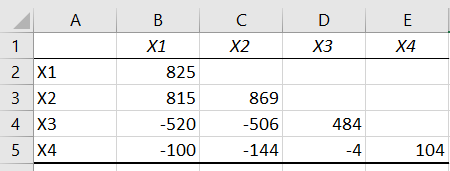
نکته: کوواریانس بین متغیر با همان واریانس خواهد بود. از طرفی چون کوواریانس خاصیت تقارن دارد، کوواریانس مربوط به بالای قطر اصلی نمایش داده نشده است.
برای محاسبه ضریب همبستگی نیز کافی است همین مراحل را طی کرده و گزینه Correlation را از پنجره Data Analysis انتخاب کنید. تنظیمات پنجره Correlation برای محاسبه ضریب همبستگی، نیز درست به مانند کوواریانس است. خروجی اجرای این دستور برای دادههای قبلی به صورت زیر خواهد بود.
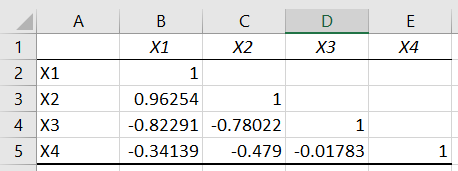
نکته: در جدول یا ماتریس حاصل از محاسبه ضریب همبستگی، بالای قطر اصلی به علت تقارن نمایش داده نشده است. همچنین ضریب همبستگی هر متغیر با خودش نیز برابر با ۱ خواهد بود، زیرا صورت و مخرج کسر محاسباتی برای ضریب همبستگی برابرند.
اگر مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای آمار، احتمالات
- آموزش محاسبات آماری در اکسل
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش استفاده از توابع و فرمول نویسی در اکسل
- آموزش مقدماتی اکسل (Excel) — به زبان ساده
- مدیریت نوار (Ribbon) اکسل با چهار ترفند کاربردی — راهنمای جامع
- فرمول نویسی در اکسل – آموزش مقدماتی
^^













سلام
وقت بخیر
درمورد محاسبه آزمون کرونباخ سوال داشتم.
پرسشنامه من شامل سوالات طیفی لیکرت و سوالات چند گزینه ای هست چطور برای سوالات چند گزینه ای باید آزمون کرونباخ را محاسبه کنم؟
سلام چرا کوواریانس بین یک مغیر با خودش برابر با واریانس است
اثباتش چگونه است
سلام و وقت بخیر،
از این که خواننده مجله فرادرس هستید، بسیار خرسندیم.
اگر به فرمول ۱ در متن محاسبه کوواریانس و ضریب همبستگی در اکسل توجه کنید، کوواریانس هر متغیر با خودش به صورت میانگین توان دوم فاصله مقادیر از میانگین در خواهد آمد که همان مفهوم واریانس است. بنابراین واریانس همان کوواریانس یک متغیر با خودش است.
از این که همراه مجله فرادرس هستید، سپاسگزاریم.
تندرست و شاد و پیروز باشید.
سلام
از چه طریقی می شود میزان تشابه بین ماتریس شماره A و B را با ماتریس شماره C نشان داد ؟
بهترین پارامتر آماری چیه و چطوری در اکسل میشه این کار انجام داد ؟
A,B دیتاهای من از دو روش هستن و C دیتاهای طبیعی هست
ابعاد ماتریس هام 5 در 5 هست و یکسان هستند
سلام و وقت بخیر
از اینکه همراه مجله فرادرس هستید بسیار خوشحالیم.
برای پاسخ به سوال شما باید بیشتر در مورد ساختار داده ها بدانیم. اگر ماتریسی که شما در نظر گرفته اید، مربوط به ۵ مشاهده است و هر ستون از ماتریس نشانگر ویژگی یا متغیرهای اندازهگیری شده هستند، تمامی روشهای اندازه گیری فاصله یا شباهت قابل استفاده است. ولی اگر ماتریسهای مورد نظر شما ماتریس کوواریانس باشند، مسئله بسیار پیچیده میشود. شاید با یک چرخش یا جابجایی سطر یا ستون هر یک از ماتریس، برابری با ماتریس دیگر مشخص شود. برای کسب اطلاعات بیشتر در موضوع بهتر است مطلب A simple procedure for the comparison of covariance matrices را مطالعه فرمایید. البته به زودی ترجمه آن در مجله فرادرس منتشر خواهد شد.
پیروز و پاینده باشید.
بسیار عالی و کاربردی توضیح داده شده بود.