سری فوریه در معادلات دیفرانسیل — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در مطالب گذشته وبلاگ فرادرس سری فوریه را توضیح دادیم. سری فوریه به منظور حل نمونه‌های خاصی از معادلات دیفرانسیل مطرح شده است. بنابراین عجیب نیست که از این مفهوم به طور گسترده برای حل معادلات دیفرانسیل با مشتقات عادی و مشتقات جزئی استفاده شود. لذا در این مطلب قصد داریم تا در مورد کاربرد سری فوریه در معادلات دیفرانسیل صحبت کنیم. البته پیشنهاد می‌شود ابتدا به ساکن مطلب سری فوریه را مطالعه فرمایید.

مقدمه

در این مطلب استفاده از سری فوریه در حل معادلات زیر را توضیح خواهیم داد.

• معادله گرما: $$ \large { \large \frac { { \partial u } } { { \partial t } } \normalsize } = k{\large\frac { { { \partial ^ 2 } u } } { { \partial { x ^ 2 } } } \normalsize} $$
• معادله موج: $$ { \large \frac { { { \partial ^ 2 } u } } {{ \partial { t ^ 2 } } } \normalsize} = \large { a ^ 2 } { \large \frac { { { \partial ^ 2 } u } } { { \partial { x ^ 2} } } \normalsize } $$
• معادله لاپلاس: $$ { \large\frac { { { \partial ^2}u}}{{\partial { x ^ 2 } } } \normalsize } + { \large \frac { { { \partial ^ 2 } u } } { { \partial { y ^ 2 } } } \normalsize } = 0 $$

مثال ۱

سری فوریه مناسب به منظور حل معادله دیفرانسیل زیر را بیابید.

$$ \large y ^ { \prime \prime } + 2 y = 3 x $$

هم‌چنین شرایط مرزی آن را به صورت زیر در نظر بگیرید.

$$ \large y ( 0 ) = y ( 1 ) = 0 $$

در این مسئله از سری فوریه سینوسی به منظور حل مسئله استفاده خواهیم کرد. در این صورت سمت راست معادله فوق را می‌توان به صورت سری فوریه، به شکل زیر نوشت.

$$ \large {3x } = { \frac { 6 } { \pi } \sum\limits _ { n = 1 } ^ \infty { \frac { { { { \left( { – 1} \right ) }^ { n + 1 }} } } { n } \sin n\pi x} }$$

حال پاسخ نهایی معادله را برابر با سری زیر در نظر می‌گیریم.

$$ \large y \left( x \right) = \sum\limits_{n = 1 } ^ \infty { { b_ n } \sin n \pi x} $$

با قرار دادن رابطه فوق در صورت سوال، رابطه زیر بدست می‌آید.

$$\large { \sum \limits _ { n = 1}^\infty {\left( { – {n^2}{\pi ^2}} \right){b_n}\sin n\pi x} }+{ 2\sum\limits _ { n = 1 } ^ \infty {{b_n}\sin n\pi x} } = {\frac{6}{\pi }\sum\limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1} \right ) } ^{ n + 1 } } } } { n } \sin n\pi x} }$$

ضرایب سینوس‌ها در دو سمت معادله باید با هم برابر باشند. بنابراین معادله مربوط به ضرایب را می‌توان به صورت زیر بیان کرد:

$$\large { \left( {2 – {n^2}{\pi ^2}} \right){b_n} = \frac { { 6 { { \left( { – 1} \right)}^{n + 1 } } } }{ { n \pi }}\;\;}\kern-0.3pt {\Rightarrow\;\;{ b _n } = \frac { { 6 { { \left( { – 1} \right)}^{n + 1 } }} } { { n \pi \left ( {2 – { n ^ 2 } { \pi ^ 2 } } \right ) } } }$$

بنابراین پاسخ معادله دیفرانسیل مذکور برابر است با:

$$\large { y \left ( x \right ) \text{ = }}\kern0pt{ \frac{6}{\pi }\sum\limits_{n = 1}^\infty { \frac { { { { \left( { – 1} \right ) } ^ { n + 1 } } } } { { n \left ( { 2 – { n ^ 2 } { \pi ^ 2 } } \right ) } } \sin n \pi x } } $$

مثال ۲

پاسخ معادله دیفرانسیل زیر را بیابید.

$$ \large y ^ { \prime } + k y = f \left ( x \right ) $$

فرض کنید $$k$$، عددی ثابت بوده و دوره تناوبِ $$f(x)$$ نیز برابر با $$2\pi$$ باشد. در اولین قدم، تابع $$f(x)$$ را برابر با سری فوریه زیر در نظر می‌گیریم.

$$\large f \left ( x \right ) = \sum \limits _ { n = – \infty } ^ \infty { { c _ n } { e ^ {inx}}} $$

از طرفی ضرایب مختلط سری فرض شده در بالا، به صورت زیر تعریف می‌شوند.

$$\large { c _ n } = \frac { 1 } { { 2 \pi } } \int \limits _ { – \pi } ^ \pi { f \left ( x \right ){ e ^ { – inx}}dx} $$

پاسخِ $$y$$ را نیز می‌توان به شکل سری زیر در نظر گرفت.

$$ \large y = \sum \limits _ { n = – \infty } ^ \infty { { y _ n } { e ^ {inx}}}$$

در نتیجه مشتق $$y$$ نیز برابر است با:

$$\large y ^{\prime} = \sum \limits _ { n = – \infty } ^ \infty { in { y _ n } { e ^{ inx}}}$$

با قرار دادن این عبارت‌ها در معادله اصلی، معادله به صورت زیر در خواهد آمد.

$$\large { \sum\limits _ { n = – \infty } ^ \infty {in { y _n } {e ^ {inx}}} } + { k \sum \limits_{n = – \infty } ^ \infty { { y _ n } { e ^ {inx}}} } = { \sum \limits _ { n = – \infty } ^ \infty {{c_n}{ e ^ {inx}}} } $$

با توجه به این که رابطه فوق به ازای تمامی مقادیر $$n$$ درست است، بنابراین می‌توان رابطه زیر را بین ضرایب عنوان کرد.

$$\large { in { y _ n } + k { y _ n } = { c _ n } \;\; \Rightarrow \;\;{y_n} = \frac { { {c _ n }} }{{in + k } } }$$

با توجه به این که اعداد $$c_n$$ و $$k$$، مقادیری معلوم هستند، نهایتا تابع $$y$$ را می‌توان به شکل زیر عنوان کرد.

$$\large y \left ( x \right ) = \sum \limits _ { n = – \infty } ^ \infty { \frac { { {c _ n }} } { { in + k } } { e ^ {inx} } } $$

مثال ۳

معادله انتقال حرارت ناپایای یک بعدی به صورت زیر است. این معادله را با توجه به شرایط مرزی $$ T (x=0) = { T _ 1 } $$، $$ T (x=L) = { T _ 2 } $$ حل کنید. هم‌چنین فرض کنید توزیع دما در لحظه اولیه برابر با $$ T \left ( { x , 0 } \right)$$ باشد.

$$\large \frac { { \partial T } } { {\partial t } } = k \frac { { { \partial ^ 2 } T } } {{ \partial { x ^ 2} } } $$

برای حل این معادله دیفرانسیل در اولین قدم باید توزیع دمای پایا را با توجه به شرایط مرزی بیان شده، بدست آورد. به منظور بدست آوردن شرایط پایا باید معادله $$ k { \frac { { { \partial ^ 2 } T } } { { \partial { x ^ 2 } } } \normalsize } = 0 $$ حل شود. با انتگرال‌گیری از این معادله، توزیع دما در حالت پایا به صورت زیر بدست می‌آید.

$$\large { T _ 0 } \left ( x \right ) = { C _ 1 } + { C _ 2 }x $$

با استفاده از شرایط مرزی ارائه شده در صورت سوال، ضرایب $$ C _ 1 = T _ 1 \ \ , \ \ C _ 2 = \frac { T _ 2 - T _ 1} { L } $$ بدست می‌آیند. بنابراین توزیع دما در حالت پایا برابر است با:

$$ { {T _ 0 } \left( x \right) = {T_1} }+{ \left( {{T_2} – {T_1}} \right)\frac{x}{L} } $$

مسئله اصلی ارائه شده در صورت سوال، وابسته به زمان است. بنابراین برای حل آن، تابعی وابسته به زمان به صورت $$ T ( x , t ) $$ تعریف می‌کنیم. در نتیجه پاسخ معادله ناپایا را می‌توان به صورت زیر نیز در نظر گرفت.

$$\large { y \left ( { x , t } \right ) } = { T \left ( { x , t } \right ) – { T _ 0 } \left( x \right) }$$

از طرفی شرایط مرزی برای تابع $$ y \left ( { x , t } \right ) $$ به صورت زیر است.

$$\large { y \left ( { 0 , t } \right ) = y \left ( { L , t } \right ) } = { 0 } $$

هم‌چنین شرط اولیه، در لحظه $$t=0$$ برابر است با:

$$\large { y \left ( { x , 0 } \right ) } = { f \left ( x \right ) – { T _ 0 } \left ( x \right ) } = { g \left ( x \right ) } $$

از طرفی توزیع دما در لحظه اولیه را نیز می‌توان بر حسب سری فوریه بیان کرد. این سری در ادامه بیان شده است.

$$ \large { g \left ( x \right ) } = { \sum \limits _ { n = 0 } ^ \infty {{b_n}\sin \frac{{n\pi x}}{ L } } } $$

توجه داشته باشید که ضرایب $$b_n$$ نیز با استفاده از مفهوم توابع متعامد و به صورت زیر بدست می‌آید.

$$\large { { b _ n } } = { \frac { 2 } { L} \int \limits _ 0 ^ L { g \left ( x \right ) \sin \frac { { n \pi x } } { L } d x } }$$

از طرفی پاسخ نهایی معادله را به صورت زیر در نظر می‌گیریم.

$$\large { y \left( {x,t} \right ) } = { \sum \limits _ { n = 0 } ^ \infty { { c _ n } \left ( t \right ) \sin \frac { { n \pi x } } {L } }}$$

بدیهی است که دو شرط مرزی $$ y \left ( { 0 , t } \right ) = 0 $$ و $$ y \left ( { L , t } \right ) = 0 $$ در تمامی زمان‌ها برقرارند، بنابراین می‌توان شرایط اولیه برای $$ { c _ n } \left ( t \right ) $$ را به صورت زیر بیان کرد:

$$ { { c _ n } \left ( 0 \right ) = { b _ n } \ \ ,\;\;\;}\kern-0.3pt {n = 0,1,2, \ldots }$$

با قرار دادن پاسخ فرض شده در معادله $$ k \frac { { { \partial ^ 2 } y } } { { \partial { x ^ 2 } } } \normalsize = \frac { { \partial y } } { { \partial t } } \normalsize $$، معادله نهایی سری برابر می‌شود با:

$$\large { - k \sum \limits _ { n = 0 } ^ \infty { \frac { { { n ^ 2 } { \pi ^ 2 } } } {{ { L ^2 } } }{ c _ n } \left ( t \right ) \sin \frac { { n \pi x } } { L } } } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { d { c _ n } \left ( t \right ) } }{ { d t } } \sin \frac { { n \pi x } }{ L } } } $$

با ضرب کردن طرفین رابطه فوق در $$ { \sin { \large \frac { { m \pi x } } { L } \normalsize}}$$ و انتگرال‌گیری در بازه $$\left[ {0,L} \right]$$، معادله به صورت زیر در خواهد آمد.

$$ \large \begin {align*} - k \sum \limits _ { n = 0 } ^ \infty { \frac { { { n ^2 } { \pi ^ 2 }} } { { { L ^ 2} } } {c _ n } \left ( t \right ) \cdot \kern0pt{ \int\limits_0^L {\sin \frac { { n\pi x } } { L } \sin \frac{{m\pi x}}{L}dx} } } = {\sum\limits _ { n = 0 } ^ \infty { \frac { {d {c _ n } \left( t \right)}}{{dt}} \cdot}\kern0pt { \int \limits _ 0 ^ L { \sin \frac { { n \pi x } } { L } \sin \frac { { m \pi x } } { L }d x } } } \end {align*} $$

رابطه فوق را می‌توان با استفاده از مفهوم تعامد به صورت زیر بیان کرد:

$$\large – k \frac { { { m ^ 2 } { \pi ^ 2 } } }{ { { L^ 2 } }} { c _ m } \left ( t \right ) = \frac { { d {c _ m } \left ( t \right ) } } {{ d t } }$$

با حل معادله دیفرانسیل ساده بالا، ضرایب $$c_m(t)$$ برابر خواهند بود با:

$$\large \begin {align*} \frac { { d { c _m } } } { { { c _m } } } & = – \frac { { k {m ^ 2 } {\pi ^2}}}{{{L^2}}}dt \\ & \Rightarrow \int {\frac{{d { c_ m } }} { { { c _m } } } } = – \frac{{k{m^2}{\pi ^2 } } } { { { L ^ 2 } } } \int { d t } \;\; \\ & \Rightarrow \ln {c_m}\left ( t \right ) = – \frac{ { k {m ^ 2 } { \pi ^ 2 }} }{ {{L ^2} } } t + { C _0 } \\ & \Rightarrow { { c _ m } \left ( t \right ) = A \exp \left( { – \frac{{k { m ^ 2 } { \pi ^ 2 } } } { { { L ^2 } } } t } \right ) } \end {align*} $$

در حالتی که $$n=m$$ باشد، ضرایب $$c_n$$ (عبارت فوق) را می‌توان به صورت زیر بازنویسی کرد.

$$\large { c _ n } \left ( t \right ) = A \exp \left( { – \frac { { k { n ^ 2 } { \pi ^ 2 } } } { { { L^ 2 } } } t } \right) $$

در رابطه بالا $$ A = { e ^{ {C _ 0 } } } $$، نشان دهنده عددی ثابت است که وابسته به مقدار اولیه است. با توجه به مقدار اولیه $$ { c _ n } \left ( 0 \right ) = { b _n } $$، پاسخ $$c_n(t)$$ را می‌توان به صورت زیر در نظر گرفت.

$$ \large { c _ n } \left ( t \right ) = { b _ n } \exp \left ( { – \frac { { k{ n ^ 2} { \pi ^2 }} } { {{ L ^ 2 } } } t } \right ) $$

با بدست آمدن $$c_n(t)$$، پاسخ نهایی توزیع دما، مطابق با رابطه زیر بدست خواهد آمد.

$$ \large \begin {align*} T \left ( { x , t } \right ) & = \kern0pt{ { T _ 0 } \left ( x \right ) + \sum \limits _ { n = 0 } ^ \infty { { b _ n } \exp \left ( { – \frac { { k{ n ^ 2} { \pi ^ 2
}} } { { { L ^ 2 } } } t } \right ) \sin \frac { { n \pi x } } { L} } } \\ & = { { T_ 1 } + \left( {{T_2} – { T _ 1 } } \right) \frac { x } { L } }+{ \sum\limits_{n = 0}^\infty { { b _ n } \exp \left ( { – \frac { {k { n ^2 } { \pi ^ 2 } } } { {{ L ^ 2 } } } t } \right ) \sin \frac { { n \pi x } } { L} } } \end {align*} $$

مثال ۴

سوال: پاسخ معادله موج برای سیمی که در دو سمت ثابت شده را بیابید. معادله موج را می‌توان به صورت زیر بیان کرد:

$$ \large {\frac { { { \partial ^ 2 } u} } { { \partial { t ^ 2 } } } = { a ^ 2 } \frac { { { \partial ^ 2 }u } } { { \partial { x ^ 2 } } } \ \ , \;\;}\kern-0.3pt{0 \le x \le L}$$

با توجه به ثابت بودن سیم در دو سمت، شرایط مرزی برای این مسئله را برابر با $$ u \left( { 0 , t } \right ) = u \left ( { L , t } \right ) = 0 $$ در نظر بگیرید. هم‌چنین فرض کنید جابجایی و سرعت اولیه مطابق با روابط زیر تعریف شده‌اند.

$$ \large { u \left ( { x , 0 } \right ) = f \left ( x \right ) \ \ , \;\;} \kern0pt {\frac { { \partial u \left ( { x , 0 } \right ) } }{ { \partial t } } = g \left ( x \right ) } $$

توجه داشته باشید که توابع $$ f ( x ) $$ و $$ g ( x ) $$ معلوم بوده و شرایط مرزی آن‌ها نیز به صورت زیر است.

$$ \large { f \left ( 0 \right ) = f \left ( L \right ) } = { g \left ( 0 \right ) } = { g \left ( L \right ) } = { 0 } $$

پاسخ: در این مسئله از روش جداسازی متغیر‌ها استفاده می‌کنیم. البته در مطلب معادله لاپلاس، این روش به تفصیل توضیح داده شده است. در این روش پاسخ را به صورت حاصل‌ضرب دو تابع وابسته به $$t$$ و $$x$$ در نظر می‌گیریم. در حقیقت شکل تابع به صورت زیر فرض می‌شود.

$$\large u \left ( { x , t } \right ) = X \left ( x \right ) \cdot T \left ( t \right )$$

در این صورت مشتقات جزئی تابع $$u$$ به صورت زیر قابل بیان هستند.

$$ \large { \frac { { { \partial ^ 2 } u } } { { \partial { t ^ 2 } } } = XT^{\prime\prime}\;\;} , \ \ \kern-0.3pt{\frac{{{\partial ^2}u}}{{\partial {x^2}}} = X ^ { \prime \prime}T }$$

در نتیجه با قرار دادن تابع فرض شده در معادله اصلی، به معادله زیر خواهیم رسید.

$$\large { { X T ^ { \prime \prime } = { a ^ 2 }X ^ { \prime \prime } T \;\;\;}}\kern-0.3pt \Rightarrow \ \ \kern-0.3pt {{\frac{{X^{\prime\prime}}}{X} = \frac { { T ^ { \prime \prime } } }{{ {a ^ 2 }T } } }}$$

همان‌طور که می‌بینید تابع قرار گرفته در سمت چپ تنها وابسته به $$x$$ و تابع سمت راست وابسته به $$t$$ است. از طرفی با توجه به برابر بودن این دو تابع، می‌توان نتیجه گرفت که نهایتا سمت راست معادله باید برابر با عدد ثابت $$\alpha$$ باشد. لذا معادله فوق را می‌توان به صورت زیر بازنویسی کرد.

$$ \large { \frac { { X ^ { \prime \prime } } } { X } = \frac { { T ^ { \prime \prime } } } { { { a ^ 2 } T } } } = { \text{const} } = { \alpha } $$

اگر مقدار $$\alpha$$ مثبت باشد در این صورت می‌توان آن را به صورت $$ \alpha = { \lambda ^ 2 } $$ در نظر گرفت. در نتیجه معادله $$T$$ به صورت زیر در خواهد آمد.

$$\large T ^ { \prime \prime } = { a ^ 2 } { \lambda ^ 2 } T $$

پاسخ عمومی معادله فوق برابر است با:

$$ \large { T \left ( t \right ) } = { a \sinh \left ( { a \lambda t } \right ) } + { b \cosh \left ( { a \lambda t } \right) } $$

همان‌طور که می‌بینید، معادله بدست آمده، قالبی هذلولوی دارد. بنابراین مرتبا مقدار آن با زمان افزایش یافته و متناوب نیست. افزایش پیوسته تابع با موجی بودن پاسخ در تناقض است؛ لذا $$ \alpha = – { \lambda ^ 2 } $$ را برابر با عددی منفی در نظر می‌گیریم. با این فرض دو معادله مربوط به $$X$$ و $$T$$ به صورت زیر بدست خواهد آمد.

$$ { X ^ { \prime \prime } + { \lambda ^ 2 } X = 0 \ \ ,\;\;\;}\kern-0.3pt { T ^ { \prime \prime } + { a ^ 2 } { \lambda ^ 2 } T = 0 } $$

بنابراین پاسخ $$X$$ برابر است با:

$$\large { X \left ( x \right ) } = { { C _ 1 } \cos \lambda x + { C _ 2 } \sin \lambda x } $$

در رابطه فوق مقادیر $$C_1$$ و $$C_2$$، ثابت‌های انتگرال‌گیری هستند. با توجه به شرایط مرزی، شرایط مرزی مربوط به $$X$$ نیز به صورت زیر بدست می‌آید.

$$ X \left ( 0 \right ) = X \left ( L \right ) = 0 $$

بنابراین رابطه مربوط به ثابت‌ها نیز به صورت زیر بدست می‌آید.

$$ { X \left ( 0 \right ) = { C _ 1 } = 0 \ \ \ , \;\;\;}\kern-0.3pt { { X \left ( L \right ) = { C _ 2 } \sin \lambda L } = { 0 } } $$

با فرض $$ { C _ 2 } \ne 0 $$، باید $$ \lambda L = \pi n $$ را فرض کرد؛ در این صورت مقادیر ویژه به صورت زیر بدست می‌آیند.

$$ { { \lambda _ n } = \frac { { \pi n } } { L } \ \ , \;\;\;} \kern-0.3pt {n = 1 , 2 , 3 , \ldots } $$

توابع ویژه مرتبط با مقادیر فوق برابرند با:

$$ \large { X _ n } \left ( x \right ) = \sin \frac { { \pi n x } }{ L } $$

با توجه به مقدار ویژه بدست آمده، توابع $$T_n$$ نیز برابر با عبارات زیر بدست می‌آیند.

$$ \large { { { T _ n } } = { { A _ n } \cos a { \lambda _ n } t } + { { B _ n } \sin a { \lambda _ n } t } } = { { A _ n } \cos \frac { { a \pi n t } } { L } } + { { B _ n } \sin \frac { { a \pi n t } } { L } } $$

بنابراین نهایتا توابع $$ u _ n ( x , t ) $$ برابرند با:

$$ \large \begin{align*} { u \left ( { x , t } \right ) } & = { \sum \limits _ { n = 1 } ^ \infty { { u _ n } \left ( { x , t } \right ) } } \\ & = { \sum\limits_{n = 1}^\infty {\sin \frac{{\pi nx}}{L}\left( {{A_n}\cos \frac { { a \pi n t } } { L} } \right.} } + { { \left. { { B
_ n } \sin \frac { { a \pi n t } } {L } } \right ) } } \end {align*} $$

فرض بر این است که تابع $$u$$ مشتق‌پذیر است؛ بنابراین مشتق زمانی تابع $$u$$ برابر است با:

$$ \large \begin {align*} \frac { { \partial u \left ( { x , t } \right ) } } { { \partial t } } & = \kern0pt { \sum \limits _ { n = 1 } ^ \infty { \sin \frac { { \pi n x } } { L } \left ( { – { A _ n } \frac { { a \pi n } }{ L } \sin \frac { { a \pi n t } } { L } } \right.} + { \left.{ { B _ n } \frac{{a\pi n}}{L}\cos\frac{{a\pi nt}}{L}} \right) } } \end {align*} $$

در این حالت ضرایب $$A_n$$ و $$B_n$$ باید با استفاده از شرایط اولیه و به صورت زیر محاسبه شود. توجه داشته باشید که توابع $$f(x)$$ و $$g(x)$$ باید با استفاده از توابعی متعامد بیان شوند. با استفاده از این مفهوم، ضرایب $$A_n$$ و $$B_n$$ به صورت زیر بدست می‌آیند.

$$\begin {align*} { { A _ n } }={ \frac{2}{L}\int\limits_0^L {f\left( x \right)\sin \frac { { \pi n x } } { L } d x } ,\;\;} {n = 1 , 2 , 3 , \ldots } \\ \kern-0.3pt {{B_n} }={ \frac { 2 } { { a \pi n } } \int \limits _ 0 ^ L { g \left( x \right) \sin \frac { { \pi n x } } {L } d x } , \;\;}\kern0pt {n = 1 , 2 , 3 , \ldots } \end {align*} $$

بنابراین نهایتا پاسخ معادله موج، با توجه به شرایط مرزی و شرایط اولیه، مطابق با رابطه زیر بدست می‌آید.

$$ \large { u \left( { x , t } \right ) = \sum \limits _ { n = 1 } ^ \infty { { u _ n } \left( { x , t } \right)} } = { \sum \limits _ { n = 1}^\infty {\sin \frac{{\pi n x } } { L } \left( { { A
_n } \cos \frac{{a\pi nt}}{L} }\right.}}+{{\left.{ {B_n}\sin\frac{{a\pi n t } } { L } } \right)} } $$

مثال ۵

پاسخ معادله لاپلاس زیر را درون ناحیه $$ { x ^ 2 } + { y ^ 2 } \le 1 $$ بیابید.

این ناحیه بیانگر دیسکی است که در ادامه نشان داده شده است.

$$\large \begin {align*} \frac { { { \partial ^ 2 } u } } { { \partial { x ^ 2 } } } + \frac { { { \partial ^ 2 } u } }{ { \partial { y ^2 } } } = 0 \end {align*} $$

شرایط مرزی را روی مرز دایره به صورت زیر در نظر بگیرید.

$$\large { \left . { u \left ( { x , y } \right ) } \right | _ { { x ^ 2 } + { y ^ 2 } = 1 } } = f \left ( { x , y } \right ) $$

با توجه به دایره‌ای بودن ناحیه، بهتر آن است که معادله توصیف کننده آن در مختصات قطبی بیان شود. همان‌طور که پیش‌تر نیز بیان شده، رابطه بین مختصات‌ دکارتی و قطبی به صورت زیر نشان داده می‌شود.

$$ \large { x = r\cos \varphi ,\;\;\;} \kern-0.3pt { y = r \sin \varphi } $$

در ادامه تصویر ناحیه‌ای که معادله روی آن حل می‌شود، نشان داده شده است.

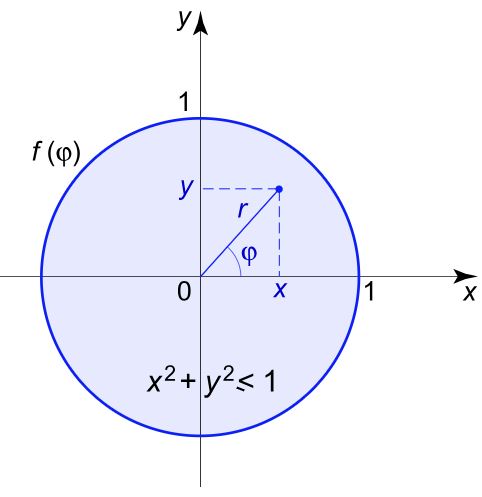
در مختصات قطبی تابع $$u(x,y)$$ به تابع $$u(r,\phi)$$ تبدیل می‌شود. بدیهی است که $$ u \left ( { r , \varphi } \right ) $$ تابعی با دوره تناوب $$2 \pi$$ محسوب می‌شود (در این مسئله). تابع $$f(\phi)$$ نیز تابعی متناوب با دوره تناوب $$2\pi$$ محسوب می‌شود. توجه داشته باشید که معادله لاپلاس در مختصات قطبی به صورت زیر بدست می‌آید.

$$ \large { { r ^ 2 } \frac{{{\partial ^2}u}}{{\partial {r^2}}} + r \frac { { \partial u } }{ { \partial r } } } + { \frac { { { \partial ^ 2 } u }} { { \partial { \varphi ^ 2 } } } } = { 0 } $$

در حقیقت ما به دنبال سری فوریه‌ای به صورت $$ \large u \left ( { r , \varphi } \right ) $$، به عنوان پاسخ معادله هستیم. همان‌طور که از معادله نیز می‌توان دید ضرایب $$a_n(r)$$ و $$b_n(r)$$ وابسته به شعاع $$r$$ هستند. با مشتق‌گیری از تابع فرض شده در بالا نسبت به $$r$$ و $$\phi$$ داریم:

$$ \large { \frac { { \partial u } } { { \partial r } } } = { \frac { { { a ^ { \prime } _ 0 } \left ( r \right ) } } { 2 } \text{ + } } \kern0pt { \sum \limits _ { n = 1 } ^ \infty {\left[ { { a ^ { \prime } _ n } \left( r \right) \cos n \varphi } \right . } + { \left. { {b ^ { \prime } _ n } \left ( r \right ) \sin n \varphi } \right ] } } $$

$$ \large {\frac { { { \partial ^2}u}}{{\partial {r^2}}} }={ \frac{{{a^{\prime\prime}_0} \left( r \right ) } } { 2 } \text{ + }}\kern0pt{ \sum\limits_{n = 1}^\infty {\left[ { { a ^ { \prime \prime } _ n } \left ( r \right ) \cos n \varphi }\right.}+{\left.{ {b ^ { \prime \prime } _ n } \left ( r \right ) \sin n \varphi } \right] } ,}$$

$$ \large { \frac { { \partial u } } { { \partial \varphi } } \text{ = }}\kern0pt{ \sum\limits_{n = 1 } ^ \infty {\left[ { – {a_n}\left ( r \right)n\sin n\varphi }\right.}}+{{\left.{ {b_n}\left( r \right ) n \cos n \varphi } \right] } } $$

$$ \large { \frac { { { \partial ^ 2 } u } } { { \partial { \varphi ^ 2 } } } \text { = } } \kern0pt { \sum \limits _ { n = 1 } ^ \infty { \left[ { – { a _ n } \left ( r \right){n^2}\cos n\varphi }\right. } } -{ { \left. { { b _ n } \left ( r \right ) { n ^ 2 } \sin n \varphi } \right]} } $$

با قرار دادن عبارت‌های فوق در معادله لاپلاس، معادله دیفرانسیل ضرایب برابر می‌شوند با:

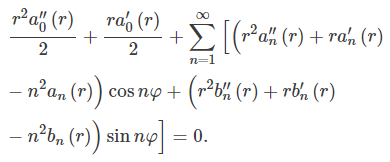
با توجه به این‌که عبارت فوق به ازای تمامی مقادیر $$r$$ و $$\phi$$ صفر هستند، بنابراین می‌توان دو معادله زیر را به منظور بدست آوردن ضرایب نوشت.

$$\large { { r ^ 2 } { a ^ { \prime \prime } _ n } \left ( r \right ) + r { a ^{\prime} _ n } \left( r \right) }-{ { n ^ 2 } { a _ n } \left ( r \right ) = 0 \; \; }\kern-0.3pt \ {,\;\;n = 0,1,2,3, \ldots }$$

$$\large { { r ^ 2 } { b ^ { \prime \prime } _ n } \left ( r \right ) + r { b ^{\prime}_n} \left( r \right) } - { { n ^2 } { b _ n } \left ( r \right ) = 0 \;\; } \kern-0.3pt \ \ {,\;\;n = 1,2,3, \ldots } $$

همان‌طور که می‌بینید با استفاده از روش به کار گرفته شده به جای حل یک معادله با مشتقات جزئی به معادله‌‌ای با مشتقات کامل رسیده‌ایم. مزیت کامل بودن مشتق این است که می‌توان آن‌‌ها به صورت مستقل نسبت به یکدیگر حل کرد. به طور مستقیم می‌توان دید که توابعی به شکل زیر در معادله اصلی صدق می‌کنند.

$$ \large { { a _ n } \left( r \right) = { a _ n } \left ( 1 \right ){ r ^ n } ,\;\;\;} \kern0pt { { b _ n } \left ( r \right ) = { b _ n } \left ( 1 \right ) { r ^ n } } $$

در معادلات فوق، ضرایب $$ { a _ n } \left ( 1 \right ) $$ و $$ { b _ n } \left ( 1 \right ) $$ با توجه به شرایط اولیه بدست می‌آیند. به منظور بدست آوردن شرایط اولیه، باید تابع $$ f \left ( \varphi \right ) = u \left ( { 1 , \varphi } \right ) $$ را به صورت سری فوریه بسط داد. در نتیجه شکل فوریه شرط مرزی برابر است با:

$$ \large \begin {align*} f\left( \varphi \right ) & = { \frac { { { \alpha _ 0 }} }{ 2 } } + { { \sum \limits _ { n = 1 } ^ \infty {\left( {{\alpha _ n} \cos n\varphi }\right . } + { \left . { { \beta _ n } \sin n\varphi } \right)} }} \\ & = {{u\left( {1,\varphi } \right) } = {\frac { { { a _ 0 } \left( 1 \right)}}{2} } } + { { \sum \limits_{n = 1}^\infty {\left[ {{a_n}\left( 1 \right)\cos n\varphi }\right.}+{\left.{ { b _ n } \left ( 1 \right ) \sin n \varphi } \right] } } } \end {align*} $$

با برابر قرار دادن ضرایب $$\sin n\phi$$ و $$\cos n\phi$$ در دو سمت معادله، رابطه بین ضرایب به صورت زیر بدست خواهند آمد.

$$ \large { { a_ n } \left ( 1 \right ) = {\alpha _ n } ,\;\;\;} \kern-0.3pt {n = 0,1,2,3, \ldots } $$

$$\large { { b _ n } \left ( 1 \right ) = { \beta _ n } ,\;\;\;} \kern-0.3pt { n = 1 , 2 , 3 , \ldots } $$

بنابراین پاسخ سیستم $$ODE$$، برابر با دو عبارت زیر است.

$$ \large { a _ n } \left ( r \right ) = { \alpha _ n } { r ^ n } ,\;\;{ b _ n } \left ( r \right ) = { \beta _ n } { r ^ n } $$

نهایتا پاسخ معادله لاپلاس برابر است با:

$$ \large { u \left( {r,\varphi } \right) = \frac{{{\alpha _ 0 } } } { 2 } } + { \sum \limits _ { n = 1} ^ \infty { { r ^ n } \left ( { { \alpha _ n } \cos n \varphi } \right.} + { \left. { { \beta _ n } \sin n\varphi } \right ) } } $$

در رابطه فوق $$ \alpha _ n $$ و $$ \beta _ n $$ اعدادی معلوم هستند که با توجه به شرایط مرزی تعیین می‌شوند. با قرار دادن $$ \alpha _ n $$ و $$ \beta _ n $$ در رابطه بالا، شکل صریح این معادله برابر است با:

$$ \large { u \left ( { r , \varphi } \right ) = } \kern0pt {{\frac{1}{\pi }\int\limits_{ – \pi }^\pi { f \left ( t \right ) \Big[ {\frac { 1} {2 } }} \text{ + } } } \kern0pt { { { { \sum\limits _ { n = 1 } ^ \infty { { r ^ n } \Big( { \cos n t \cos n \varphi } } \text{ + }}}\kern0pt{{{{ \sin n t \sin n \varphi } \Big ) } } \Big] d t } } } $$

از طرفی از مثلثات می‌دانیم که رابطه زیر را می‌توان برای تفاضل دو زاویه نوشت:

$$ \large { \cos n t \cos n \varphi } + { \sin n t \sin n \varphi } = { \cos n \left ( { t – \varphi } \right ) } $$

بنابراین تابع $$u$$ را می‌توان به صورت زیر نوشت:

$$ \large { u \left ( { r , \varphi } \right) \text { = } } \kern0pt{ \frac{1}{{2\pi } } \int \limits _ { – \pi } ^ \pi { f \left ( t \right)\Big[ {1 \text{ + } } } } \kern0pt{{{ 2 \sum\limits _ { n = 1 } ^ \infty { {r ^ n } \cos n \left ( { t – \varphi } \right ) } } \Big] d t } } $$

با استفاده از رابطه $$ \cos x = { \large \frac { { { e ^ { i x } } + { e ^ { – i x } } } }{ 2 } \normalsize} $$، می‌توان انتگرال فوق را محاسبه کرد. به طور دقیق‌تر می‌توان گفت که عبارت درون براکت را می‌توان به صورت زیر نوشت:

$$ \large {1 + 2 \sum \limits _ { n = 1 } ^ \infty {{r^n}\cos n\left( {t – \varphi } \right)} } = { \frac { { 1 – { r ^ 2 } } } { { 1 – 2r\cos \left( {t – \varphi } \right) + { r ^2 } } } }$$

در نتیجه حاصل انتگرال نیز به صورت زیر در خواهد آمد.

$$ \large {u\left( { r , \varphi } \right) \text { = }}\kern0pt { \frac { 1 } { { 2 \pi }}\int\limits_{ – \pi } ^ \pi { f \left( t \right) \cdot} \kern0pt{ \frac{{1 – { r ^ 2 } } } { { 1 – 2 r \cos \left( {t – \varphi } \right ) + { r ^ 2 } } } d t } } $$

به عبارت فوق انتگرال پواسون گفته می‌شود.