خازن سری — به زبان ساده (+ دانلود فیلم آموزش رایگان)
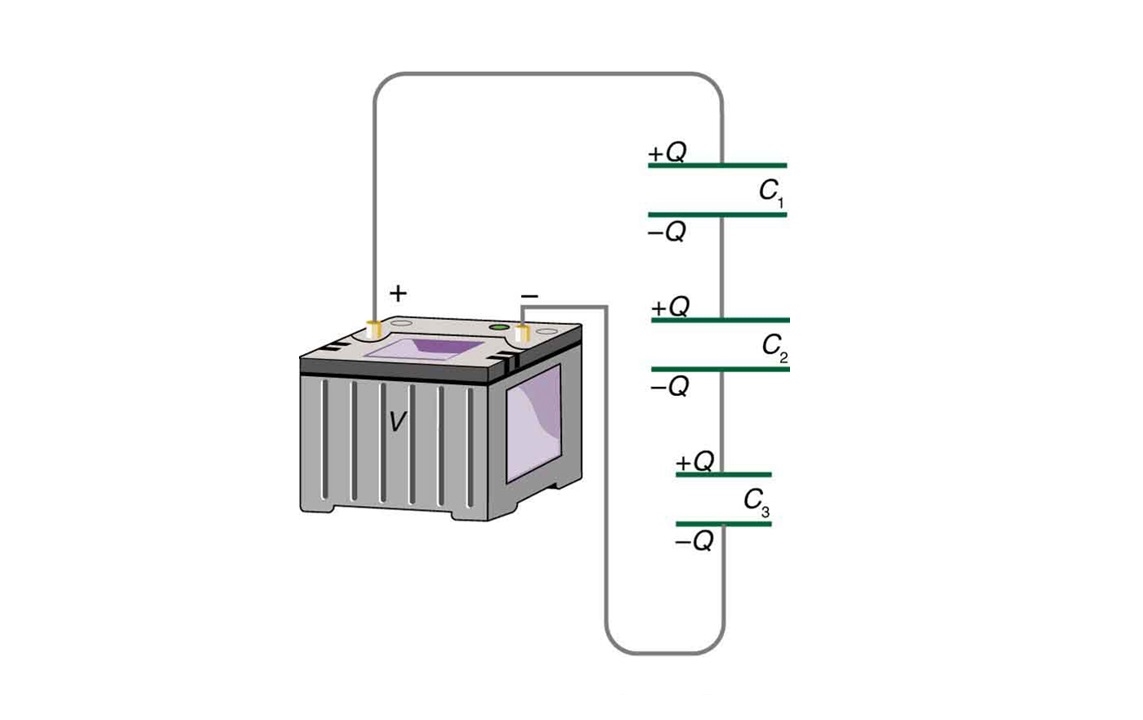
در آموزشهای قبلی مجله فرادرس، با مقاومتهای سری و موازی آشنا شدیم. در این آموزش با تحلیل دو یا چند خازن سری و به دست آوردن معادل آنها آشنا میشویم.
فیلم آموزشی خازن سری
خازن سری
جریان عبوری از خازنهایی که به صورت سری با یکدیگر متصل شدهاند، یکسان است؛ زیرا در این حالت، تنها یک مسیر برای عبور جریان وجود دارد. برای مثال: $$ i _ T = i _ 1 = i _ 2 = i _ 3 =\cdots $$. بنابراین، در هر خازن، بدون توجه به مقدار ظرفیتی که دارد، بار الکتریکی $$ Q$$ مشابهی روی صفحات ذخیره میشود. دلیل این امر آن است که بار ذخیره شده صفحات هر خازن باید از صفحه خازن مجاور بیاید. بنابراین، بار خازنهای سری باید با یکدیگر برابر باشد:
$$ \large Q _ T = Q _1 = Q _ 2 = Q _ 3 = \cdots $$
مدار شکل زیر را در نظر بگیرید که در آن، سه خازن به صورت سری با یکدیگر متصل شدهاند و به دو طرف مجموعه آنها یک ولتاژ اعمال کردهایم.
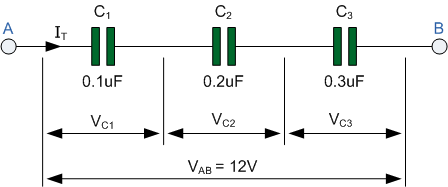
در مدار سری بالا، صفحه سمت راست خازن $$C_1$$ به صفحه سمت چپ خازن $$C _ 2 $$ متصل است. صفحه سمت راست خازن $$ C _ 2 $$ نیز به صفحه سمت چپ خازن $$ C _ 3 $$ اتصال دارد. در نتیجه، در این اتصال سری مدار DC، خازن $$C_ 2$$ از مدار ایزوله شده است. نتیجه این امر آن است که سطح مؤثر صفحه به کوچکترین خازن در ترکیب سری خازنها کاهش یافته است. بنابراین، افت ولتاژ هر خازن، بسته به مقدار ظرفیتی که دارد، متفاوت خواهد بود.
با اعمال قانون ولتاژ کیرشهف (KVL) به مدار بالا، داریم:
$$ \large V _ \text {AB} = V _ \text {C1} + V _ \text {C2} + V _ \text {C3} = 12\, \text{V} $$
$$ \large V _ \text {C1} = \frac {Q _ \text{T} } {C _ 1 } , \;\;\;\; V _ \text {C2} = \frac {Q _ \text{T} } {C _ 2 } , \;\;\;\; V _ \text {C3} = \frac {Q _ \text{T} } {C _ 3 } $$
از آنجایی که $$ Q = C \times V $$ و با نوشتن آن به صورت $$ V = Q / C $$ و جایگذاری $$ Q / C $$ در ولتاژ $$ V _ \text{C}$$ هر خازن، معادله KVL بالا به صورت زیر در میآید:
$$ \large V _ \text {AB} = \frac {Q _ \text{T} } {C _ \text{T} } = \frac {Q _ \text{T} } {\text{C}_1 } + \frac {Q _ \text{T} } {\text{C}_2 } + \frac {Q _ \text{T} } { \text{C}_3 }$$
با تقسیم دو طرف رابطه بالا بر $$ Q _ \text{T}$$، به معادله اساسی زیر برای خازنهای سری خواهیم رسید:
$$ \large \boxed {\frac {1 } {C _ \text{T} } = \frac {1 } {\text{C}_1 } + \frac {1} {\text{C}_2 } + \frac {1 } { \text{C}_3 } + \cdots} $$
بنابراین، وقتی خازنها را به صورت سری با یکدیگر وصل کنیم، برخلاف مقاومتها، مجموع معکوس ظرفیت آنها برابر با معکوس ظرفیت معادلشان است.
مثالها
در این بخش، دو مثال را درباره اتصال سری خازنها بیان میکنیم که نکات جالبی نیز در بر دارند.
مثال ۱
مدار شکل بالا را مجدداً در نظر بگیرید. میخواهیم خازن معادل $$ C _ \text {T}$$ را به دست آوریم. با توجه به فرمولی که در بالا ارائه شد، داریم:
$$ \large \frac {1 } {C _ \text{T} } = \frac {1 } {0.1\, \mu\text{F} } + \frac {1} {0.2\, \mu\text{F} } + \frac {1 } { 0.3\, \mu\text{F}} = \frac { 1 } { 18.33 \times 10 ^ 6 } $$
$$ \large C _ \text{T} = 0.055\, \mu \text{F} $$ یا $$ \large 55\, \text{nF} $$
یک نکته مهم درباره خازنهای سری این است که ظرفیت کل $$ C _ \text {T}$$ هر تعداد از خازنهای سری، همیشه کمتر از ظرفیت کوچکترین خازن سری در مدار است. در این مثال، $$ C _ \text{T} = 0.055\, \mu\text{F}$$ از مقدار کوچکترین خازن، یعنی $$ 0.1\, \mu \text{F}$$ کوچکتر است.
از رابطه مجموع وارون ظرفیتها میتوان برای هر تعداد دلخواه خازن سری استفاده کرد. اما اگر تنها دو خازن سری داشته باشیم، میتوانیم با استفاده از فرمول زیر، خازن معادل را سریعتر محاسبه کنیم:
$$ \large \boxed {C _ \text{T} = \frac {C _ 1 \times C _ 2 } { C _ 1 + C _ 2 } }$$
اگر ظرفیت دو خازن برابر باشد، یعنی $$ C _ 1 = C _ 2 $$، آنگاه میتوانیم معادله بالا را به فرم سادهتر زیر بنویسیم:
$$ \large C _ \text{T} = \frac { C ^ 2} { 2 C } = \frac { C } { 2 } = \frac { 1 } { 2 } C $$
همانطور که میبینیم، اگر ظرفیت دو خازن سری برابر باشد، ظرفیت معادل آنها نصف ظرفیتی است که هر یک از خازنها دارند. طبق قانون ولتاژ کیرشهف، ولتاژ اعمالی $$ V _ s $$ به مجموعه خازنهای سری، برابر با مجموع ولتاژهای دو سر هر یک از خازنها است.
راکتانس خازنی خازنهای سری، مانند امپدانسی با فرکانس منبع است. این راکتانس خازنی اختلاف ولتاژی در دو سر هر خازن تولید میکند و به همین دلیل، خازنهای سری به عنوان یک مدار مقسم ولتاژ خازنی عمل میکنند.
فرمول تقسیم ولتاژ مقاومتها را میتوان برای دو خازن سری به صورت زیر نوشت:
$$ \large \boxed { V _ \text{CX} = V _ \text {S} \frac { C _ \text{T}} { C _ \text {X}} } $$
که در آن، $$ C _ \text{X}$$ ظرفیت مورد نظر، $$ V _ \text{S}$$ ولتاژ منبع تغذیه اعمالی بر مجموعه خازنهای سری و $$ V _ \text {CX}$$ افت ولتاژ دو سر خازن مورد نظر است.
مثال ۲
ظرفیت معادل و ولتاژ RMS دو خازن سری را در دو حالت (الف) و (ب) در صورتی به دست آورید که یک منبع ولتاژ $$ 12\, \text{V} \, \text{AC}$$ به مجموعه آنها اعمال شود.
- (الف) ظرفیت هر یک از دو خازن ۴۷ نانوفارارد است.
- (ب) ظرفیت یک خازن ۴۷۰ نانوفاراد و ظرفیت دیگری ۱ میکروفاراد است.
حل (الف): طبق فرمولی که بیان کردیم، خازن معادل برابر است با:
$$ \large C _ \text {T} = \frac { C _ 1 \times C _ 2 } { C _ 1 + C _ 2 } = \frac {47 \, \text {nF} \times 47 \, \text {nF} } { 47 \, \text {nF} + 47 \, \text {nF} } = 23.5\, \text {nF} $$
افت ولتاژ دو سر خازنها نیز به صورت زیر به دست میآید:
$$ \large \begin {align*}
V _ \text{C1} & = \frac { C _ \text {T} } { C _ 1 } \times V _ \text{ T} = \frac { 23.5\, \text {nF} } { 47 \, \text {nF} } \times 12\, \text{V} = 6\, \text{V} \\
V _ \text {C2} & = \frac { C _ \text {T} } { C _ 2 } \times V _ \text{ T} = \frac { 23.5\, \text {nF} } { 47 \, \text {nF} } \times 12\, \text{V} = 6\, \text{V}
\end {align*} $$
حل (ب): ظرفیت خازنی معادل به صورت زیر محاسبه میشود:
$$ \large C _ \text {T} = \frac { C _ 1 \times C _ 2 } { C _ 1 + C _ 2 } = \frac {470 \, \text {nF} \times 1 \, \mu \text {F} } { 470 \, \text {nF} + 1 \, \mu \text {F} } = 320\, \text {nF} $$
افت ولتاژ خازنهای $$ C _ 1 = 470\, \text{nF}$$ و $$ C _ 2 = 1\, \mu\text{F}$$ برابر است با:
$$ \large \begin {align*}
V _ \text{C1} & = \frac { C _ \text {T} } { C _ 1 } \times V _ \text{ T} = \frac { 320\, \text {nF} } { 470 \, \text {nF} } \times 12\, \text{V} = 8.16\, \text{V} \\
V _ \text {C2} & = \frac { C _ \text {T} } { C _ 2 } \times V _ \text{ T} = \frac { 320\, \text {nF} } { 1 \, \mu\text {F} } \times 12\, \text{V} = 3.84\, \text{V}
\end {align*} $$
همانطور که میبینیم، با توجه به قانون ولتاژ کیرشهف، مجموع افت ولتاژهای دو خازن سری، برابر با ولتاژ اعمالی به مجموعه آنها است.
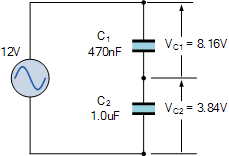
وقتی مقادیر ظرفیت دو خازن سری متفاوت باشد، خازن بزرگتر (با ظرفیت بیشتر)، در یک مقدار ولتاژ پایینتر شارژ میشود و خازن کوچکتر، با ولتاژ بالاتری همان بار را خواهد داشت. این تفاوت بین ولتاژها به این دلیل است که هر کدام از خازنها مقدار بار برابری را در صفحات خود نگه میدارند:
$$ \large \begin {align*}
Q _ \text{C1} & = V _ \text {C1} \times C _ 1 = 8.16\, \text {V} \times 470\, \text {nF} = 3.84 \, \mu \text {C} \\
Q _ \text {C2}& = V _ \text {C2} \times C _ 2 = 3.84\, \text {V} \times 1\, \mu \text {F} = 3.84 \, \mu \text {C}
\end {align*} $$
توجه کنید که نسبت ولتاژ دو خازن سری هموراه ثابت است؛ زیرا راکتانس $$ X _C$$ آنها با تغییر فرکانس منبع به نسبت برابری تغییر میکند. بنابراین، در مدار شکل بالا، ولتاژهای $$ 0.16\, \text{V}$$ و $$ 3.84\, \text{V}$$ با تغییر فرکانس منبع از $$100\, \text{Hz}$$ به $$100\, \text{kHz}$$ تغییر نمیکنند.
جمعبندی
به عنوان خلاصه میتوان گفت که جریان گذرنده از خازنهای سری با هم برابر است؛ یعنی: $$ i _ T = i _ 1 = i _ 2 = i _ 3 = \cdots $$. دو یا چند خازن سری، همواره مقدار بار یکسانی روی صفحات خود دارند.
از آنجایی که بار $$ Q $$ خازنهای سری برابر و ثابت است، افت ولتاژ هر خازن را میتوان با رابطه $$ V = Q / C $$ به دست آورد. در خازنهای سری، خازنی با ظرفیت کمتر، افت ولتاژ بیشتری دارد و خازنی با ظرفیت بزرگتر، افت ولتاژ کمتری خواهد داشت.
در آموزشهای بعدی، درباره خازنهای موازی بحث خواهیم کرد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- آموزش فیزیک پایه ۲
- آموزش مدارهای الکتریکی 1
- ال ای دی (LED) چیست؟ — به زبان ساده
- مدار مرتبه اول RC — از صفر تا صد
- الکتریسیته ساکن — به زبان ساده
^^











سلام، لطفا بفرماید، برای افزایش برق موتور سیکلت، ميشه از خازن وترانزیستور استفاده کرد، اگه ميشه برای برق Ac وبرق Dc از چه نوع خازن وترانزیستور؟ ممنون از راهنمايان
سلام استاد خسته نباشید میشه اثبات و علت این پیوستگی بگید
vc(t0^+)=vc(t0^-)
سلام.
همانطور که میدانیم، رابطه بین ولتاژ و جریان یک خازن بهصورت $$ i = C\frac {dv}{dt}$$ بیان میشود که در آن، $$C$$ ظرفیت خازن و $$ i $$ و $$ v $$، بهترتیب، جریان و ولتاژ خازن هستند. اگر ولتاژ پیوسته نباشد، یعنی مشتق آن، که جریان است، باید بینهایت شود و میدانیم که چنین چیزی ممکن نیست. در واقع، اگر بخواهیم ولتاژ یک خازن پیوسته نباشد، معادله حاکم بر آن به ما میگوید که باید منبعی با جریان بینهایت داشته باشیم. میدانیم که وجود منبع بینهایت در دنیای واقعی امکانپذیر نیست. به همین دلیل، ولتاژ خازن پیوسته است. مشابه این موضوع برای جریان سلف نیز برقرار است.
سالم و سربلند باشید.
با سلام
اصلا دلیل سری کردن خازن ها چیست؟؟
چرا باید دوتاخازن ۴ و ۱۲ میکروفاراد سری کنیم تا خازن ۳ میکروفاراد در نهایت بدست بیاریم خو از اول خازن ۳ میکرو فاراد بندازیم
منظورم اینه دلیل سری کردن چیه؟ (مزایا)
سلام.
یکی از کاربردهای سری کردن خازنها، استفاده از آنها بهعنوان مقسم ولتاژ است. علاوه بر این، گاهی به این دلیل خازنها را سری میکنیم که بتوانیم در ولتاژ بالاتر کار کنیم. برای مثال، ۳ عدد خازن یککیلوولتی سری را میتوانیم در مداری با ولتاژ ۳ کیلوولت به کار ببریم. در موارد تعداد بالا نیز، بسته به موقعیت، استفاده از خازنهای سری از نظر اقتصادی مقرون به صرفه خواهد بود.
سپاس از همراهیتان با مجله فرادرس.
واقعا ساده گفتین کاش نسبیت و فیزیک کوانتوم راهم شما درس بدین
چرا در حالت سری،ظرفیت معادل کوچکتر میشود؟
در خازن ها
سلام.
همانطور که میدانیم، فرمول ظرفیت خازن $$C=\epsilon\frac{A}{d}$$ است که در آن، $$A$$ مساحت صفحات خازن، $$d$$ فاصله بین صفحات و $$\epsilon$$ ضریب دیالکتریک برای محیط بین دو صفحه است. وقتی دو خازن را سری میکنیم، در حقیقت فاصله $$d$$ بین آنها را زیاد میکنیم و $$A$$ و $$\epsilon$$ ثابت میمانند. بنابراین، با توجه به فرمول ظرفیت خازن و رابطه عکس آن با فاصله، ظرفیت کاهش پیدا میکند.
از اینکه با مجله فرادرس همراه هستید، خوشحالیم.
چرا در حالت سری،ظرفیت معادل کوچکتر میشود؟
(در خازن ها)