تعریف مقطع مخروطی و مفاهیم مرتبط با آن — به زبان ساده

از تقاطع دادن یک صفحه با یک مخروط، می‌توان منحنی‌های مختلفی از قبیل دایره، بیضی، سهمی یا هذلولی ایجاد کرد. به هر منحنی حاصل از این تقاطع، «مقطع مخروطی» می‌گویند.

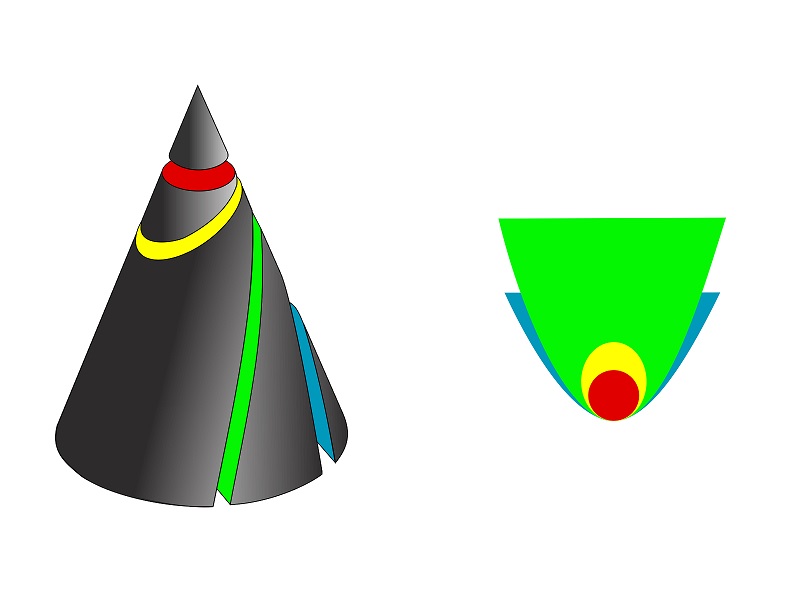
تعریف مقطع مخروطی

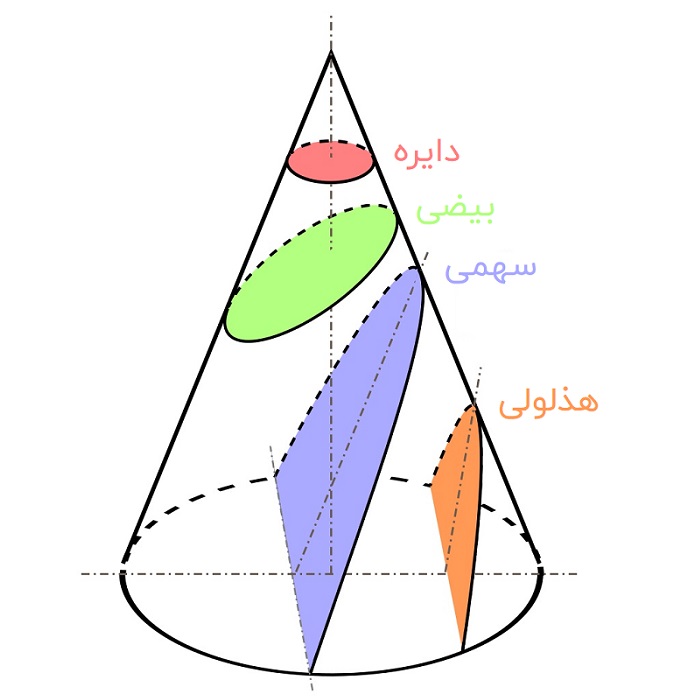
مقاطع مخروطی

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

این منحنی‌ها را می‌توان با استفاده از یک خط راست (خط هادی) و یک نقطه (نقطه کانونی) تعریف کرد. هنگامی که فاصله نقطه کانونی تا یک نقطه بر روی یک منحنی و فاصله عمودی خط هادی تا آن نقطه را اندازه‌گیری کنیم، نسبت این دو فاصله همیشه یک نسبت ثابت خواهد بود.

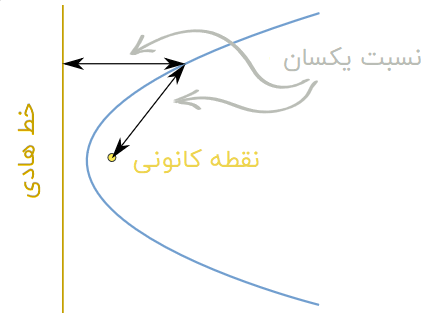
نسبت فواصل در منحنی‌های مختلف به صورت زیر است:

• بیضی: نسبت فواصل کوچک‌تر از 1 است.
• سهمی: نسبت فواصل برابر 1 است؛ بنابراین، فواصل با هم برابر خواهند بود.
• هذلولی: نسبت فواصل بزرگ‌تر از 1 است.

خروج از مرکز

نسبتی که در بالا به آن اشاره شد، «خروج از مرکز» نام دارد. با توجه به تعریف خروج از مرکز می‌توان گفت: یک مقطع مخروطی، تمام نقاطی است که فاصله آن‌ها تا نقطه کانونی برابر با حاصل‌ضرب خروج از مرکز در فاصله تا خط هادی باشد.

اگر خروج از مرکز،

• بین 0 تا 1 باشد: مقطع مخروطی، بیضی خواهد بود.
• برابر با 1 باشد: مقطع مخروطی، سهمی خواهد بود.
• بزرگ‌تر از 1 باشد: مقطع مخروطی، هذلولی خواهد بود.

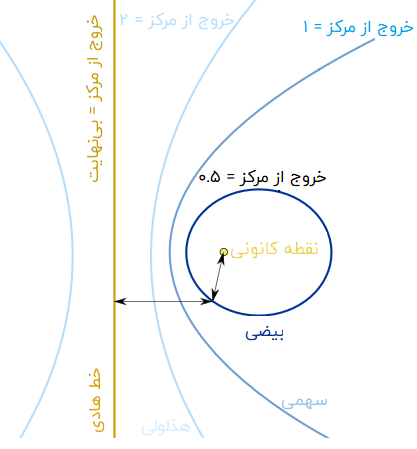
برای یک دایره، خروج از مرکز صفر خواهد بود. در نتیجه، عدد خروج از مرکز، میزان «غیر دایره‌ای» بودن یک منحنی را نشان می‌دهد. هر چه خروج از مرکز بزرگ‌تر باشد، انحنا کمتر خواهد بود.

راست وتر کانونی

«راست وتر کانونی» (Latus Rectum)، از روی نقطه کانونی می‌گذرد و با خط هادی موازی است. طول این وتر در مقاطع مخروطی مختلف به صورت زیر است:

• طول راست وتر در یک سهمی، چهار برابر فاصله کانونی است.
• طول وتر در یک دایره، قطر دایره است.
• طول وتر در یک بیضی، برابر با فرمول 2b²/a است؛ که a و b، نصف طول قطر بزرگ و کوچک هستند.

در تصویر زیر، قطرهای بزرگ و کوچک یک بیضی را مشاهده می‌کنید. در اینجا، تنها یک نقطه کانونی و خط هادی وجود ندارد، بلکه در هر طرف بیضی یک جفت از آن‌ها موجود است.

معادله عمومی مقاطع مخروطی

ما می‌توانیم معادله‌ای را ایجاد کنیم که بتواند معرف همه‌ی مقاطع مخروطی باشد.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

از آنجایی که این مقاطع، یک سری منحنی مسطح هستند، تنها به دستگاه مختصات کارتزین (استفاده از x و y برای نمایش مختصات نقاط) نیاز خواهیم داشت. از طرف دیگر، چون این منحنی‌ها در خط راست قرار ندارند، باید از عبارت‌های زیر نیز در معادله کلی استفاده کنیم:

• X² و y²،
• x (بدون y) و y (بدون x)،
• x و y با هم (xy)
• و یک عبارت ثابت.

علاوه بر این، باید برای هر یک از عبارت‌ها، یک ضریب ثابت در نظر بگیریم. با در نظر گرفتن همه این‌ها، معادله کلی معرف مقاطع مخروطی به صورت زیر درمی‌آید:

Ax² + Bxy + Cy² + Dx + Ey + F = 0

با استفاده از معادله بالا، می‌توان معادله‌های دایره، بیضی، سهمی و هذلولی را به دست آورد.

امیدواریم این مقاله مورد توجه شما قرار گرفته باشد. اگر به مطالعه بیشتر در زمینه هندسه علاقه‌مند هستید، مطالب زیر را به شما پیشنهاد می‌کنیم:

• آموزش جامع هندسه دبیرستان
• چندضلعی ها در هندسه — به زبان ساده
• هندسه فضایی و تعاریف آن — به زبان ساده
• مکعب در هندسه – مبانی، مفاهیم و محاسبات

#