اینورتر نیم پل — از صفر تا صد
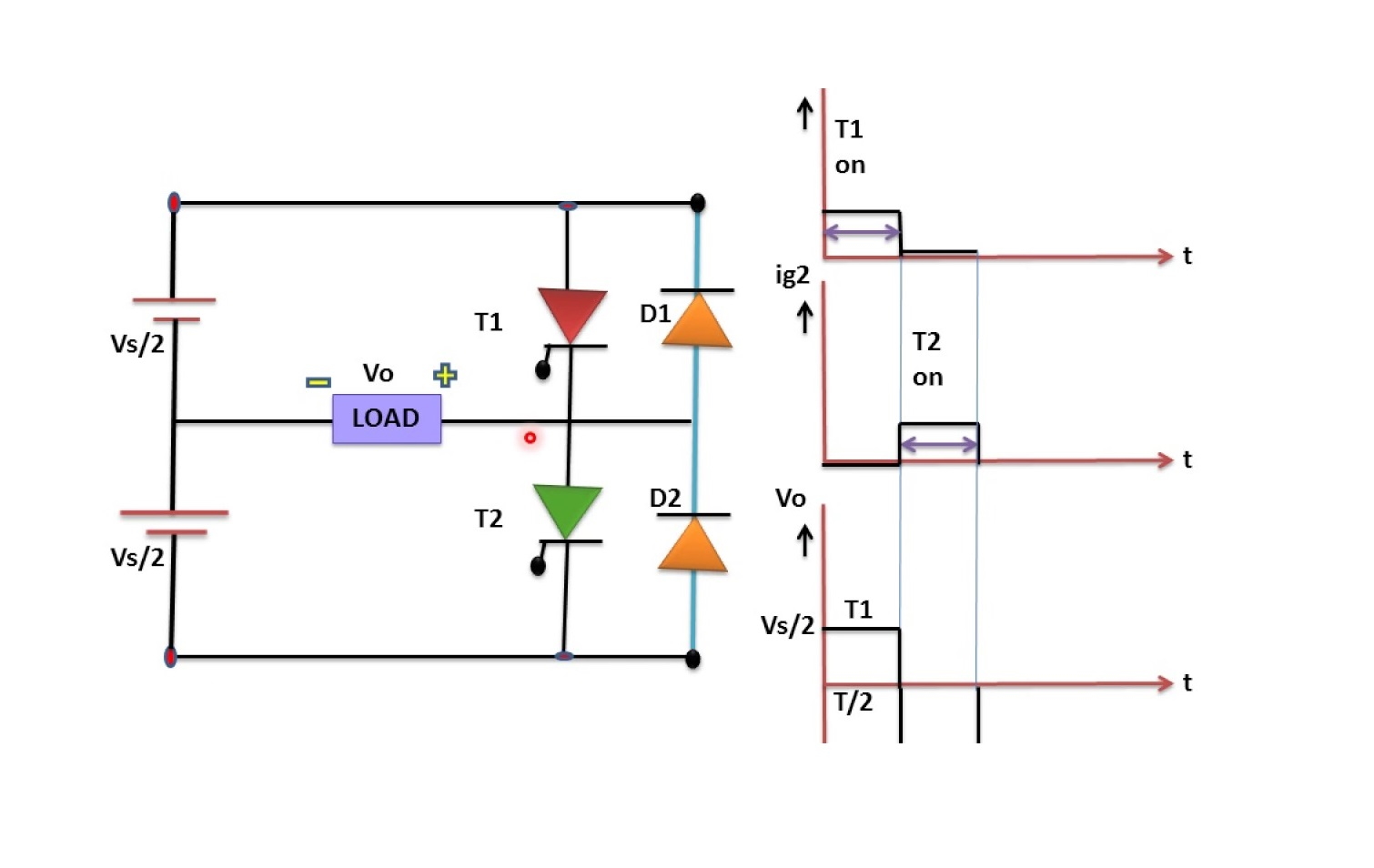
در آموزشهای پیشین مجله فرادرس با اینورتر و انواع آن آشنا شدیم. در این آموزش یکی از ساختارهای رایج اینورتر، به نام اینورتر نیم پل اچ (Half H-Bridge) را معرفی میکنیم.
اینورتر نیم پل چیست؟
نیم پل یکی از توپولوژیهای اینورتر است که DC را به AC تبدیل میکند. مدار معمولی نیم پل شامل دو سوئیچ کنترلی، تغذیه DC سه سیمه، دو دیود فیدبک و دو خازن است که بار را به منبع متصل میکنند. سوئیچ کنترل میتواند هر سوئیچ الکترونیکی مانند ماسفت، BJT، تریستور، IGBT و غیره باشد.
مدار به گونهای طراحی شده است که هر دو سوئیچ نباید در یک زمان واحد روشن شوند و فقط یکی از دو سوئیچ هدایت میکند. هر سوئیچ به مدت نیمدوره کار میکند ($$T/2$$) و نیمی از ولتاژ اعمال شده بار ($$\pm V_{dc}/2$$) را تأمین خواهد کرد. هنگامی که هر دو سوئیچ خاموش هستند، ولتاژ بار به جای $$V_{dc}/ 2 $$ برابر با $$V_ { dc } $$ خواهد بود. این مدار اینورتر نیم پل نام دارد.
در ادامه، برای سادگی از نمادگذاریهای زیر استفاده میکنیم:
- جریان گذرنده از $$ S_ 1 $$ برابر با $$ i _ 1 $$ است، در حالی که جریان عبوری از $$ S _ 2 $$ برابر با $$ i _ 2 $$ خواهد بود.
- ولتاژ و جریان خروجی به ترتیب، $$ v _ o $$ و $$ i _ o $$ هستند.
- $$T$$ دوره زمانی است و سوئیچها به صورت یکطرفه در نظر گرفته میشوند.
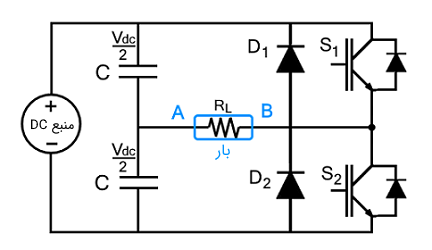
اینورتر نیم پل با بار مقاومتی
عملکرد اینورتر نیم پل با بار مقاومتی خالص سادهترین حالت عملکرد این مدار است. یک بار کاملاً مقاومتی هیچ مؤلفه ذخیرهای (سلفی و خازنی) ندارد، بنابراین مدار نیازی به دیودهای فیدبک نخواهد داشت. مدار با این بار فقط در دو وضعیت کار خواهد کرد.
وضعیت 1 ($$ 0 < t < T/2$$):
در این وضعیت، کلید $$ S_ 1 $$ در فاصله زمانی $$ t = 0 $$ تا $$ t = T / 2 $$ روشن و کلید $$ S _ 2 $$ خاموش است. به محض روشن شدن $$ S _ 1 $$، ولتاژ روی بار ظاهر میشود. ولتاژ خروجی روی بار برابر خواهد بود با:
$$ \large v _ o = v _ { d c } / 2 $$
جریان عبوری از سوئیچ $$ S _ 1 $$ نیز به صورت زیر است:
$$ \large i _ o = v _ { dc } / 2 R _ L $$
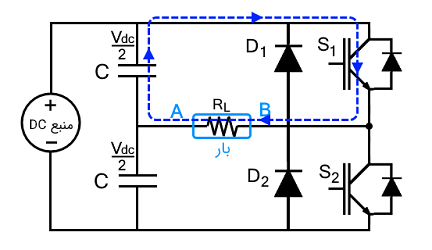
حالت 2: ($$ T / 2 < t < T $$)
شکل موج خروجی اینورتر نیم پل با بار مقاومتی $$R$$ به صورت زیر است.
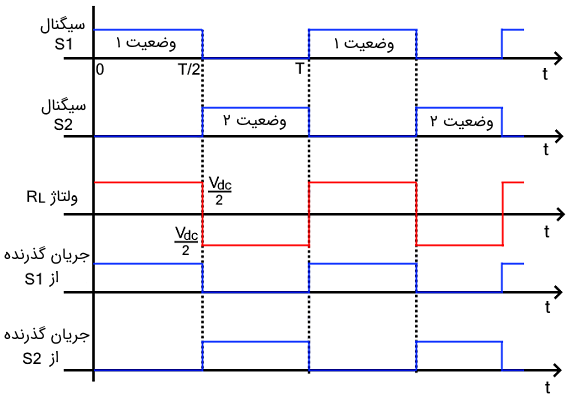
دو شکل موج اول پالسهای اعمال شده روی سوئیچها را نشان میدهند که در صورت خاموش بودن سوئیچ مکمل، هر سوییچ پالس را دریافت میکند. سومین نمودار، شکل موج ولتاژ روی بار را نشان میدهد. این شکل موج نشان میدهد که پلاریته ولتاژ با سوئیچینگ تغییر میکند. دو نمودار آخر جریان گذرنده از دو سوئیچ $$ S_ 1 $$ و $$ S_ 2 $$ را نشان میدهند.
مقدار جذر میانگین مربعات (RMS) ولتاژ خروجی را میتوان به صورت زیر محاسبه کرد:
$$ \large \sqrt {\left ( \frac {1} {T} \int _0 ^ T \frac {v _ { dc } d \theta}{4}\right )} = \frac { V _{dc}}{2} $$
برای تبدیل ولتاژ لحظهای میتوان از سری فوریه استفاده کرد:
$$ \large v _ o = a _ 0 / 2 + \sum _{n=1} ^ \infty (a_n \cos (n \omega t ) + b _ n \sin (n \omega t ) ) $$
از آنجا که هیچ آفست DC وجود ندارد، بنابراین، $$ a _ 0 $$ برابر با صفر بوده و به دلیل تقارن ربع موج، $$ a _ n $$ صفر است. بنابراین، تنها $$ b_ n $$ باقی میماند و به صورت زیر محاسبه میشود:
$$ \large b _ n = \frac 1 \pi \left [ \int _ {-\frac \pi 2 } ^ 0 \frac { - v _ {dc }} { 2 } d ( \omega t ) + \int _ 0 ^ \frac \pi 2 \frac { v _ {dc } } { 2 } d (\omega t ) \right ] = \frac { 2 v _ { dc } } { n \pi } $$
با قرار دادن مقدار $$ b _ n $$ در معادله سری فوریه، خواهیم داشت:
$$ \large v _ o = \sum _ { n = 1 } ^ \infty \left ( \frac { v _ { dc}} { n \pi} \sin n \omega t \right ) \\ \large v _ o = 0\;\; \text {for} \; n= 2 , 4 , 6 , ... $$
که در آن، $$\omega$$ فرکانس زاویهای ولتاژ خروجی است. حتی هارمونیکهای ولتاژ خروجی به دلیل تقارن موج ربعی وجود ندارد. در نتیجه، ولتاژ خروجی به صورت زیر است:
$$ \large v _ 0 = \frac { v _ { dc } } { \sqrt { 2 } \pi} = 0.45 v _ { dc} $$
بنابراین، ولتاژ خروجی تقریباً برابر با نیمی از ولتاژ اعمال شده است.
جریان گذرنده از بار مقاومتی را میتوان به راحتی با تقسیم ولتاژ RMS به مقاومت محاسبه کرد:
$$ \large i _ L = \frac 1 R \left [ \sum _ { n = 1 } ^ \infty \left ( \frac { v _{dc}} { n \pi } \sin n \omega t \right ) \right ] $$
اینورتر نیم پل با بار سلفی و سلفی-مقاومتی
عملکرد اینورتر نیم پل برای هر دو نوع بار سلفی و سلفی-مقاومتی یکسان است، زیرا نه بار القایی خالص و نه مقاومت خالص در واقعیت وجود دارد. یک سلف خالص دارای مقداری مقاومت اهمی است، بنابراین بار مقاوتی-سلفی در عمل رایجتر است.
در اینجا ما عملکرد اینورتر نیم پل با بار مقاومتی-سلفی را در نظر خواهیم گرفت. عملکرد مدار را میتوان میتوان در 4 وضعیت بررسی کرد که در آن دو وضعیت برای کنترل سوئیچها و دو وضعیت مربوط به برگشت انرژی ذخیره شده به منابع است.
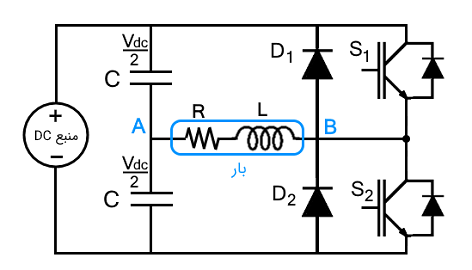
ترمینال A و B دو سر بار را نشان میدهند. در فاصله زمانی که $$S_1$$ فرمان میگیرد، A مثبتتر است، در حالی کهوقتی $$S_2$$ فعال میشود، B مثبتتر خواهد بود. در صورتی که بار مقاومتی باشد، شکل موج جریان و شکل موج ولتاژ هر دو یکسان هستند. اگر بار RL باشد، هر دو شکل موج جریان و ولتاژ همزمان به نقطه پیک نمیرسند. هنگامی که بار سلفی باشد، جریان پسفاز خواهد بود. اما وقتی بار خازنی باشد، ولتاژ پسفاز است.
هنگامی که پلاریته جریان و ولتاژ یکسان نباشد، جریان میرا از دیودهای فیدبک عبور میکند. در صورت مثبت بودن جریان، هنگامی که جریان مثبت و ولتاژ منفی باشد، دیود $$ D_ 1 $$ هدایت خواهد کرد و وقتی ولتاژ مثبت و جریان منفی است، دیود $$D_2$$ جریان را عبور میدهد.
شکل موج کمی متفاوت است، زیرا سلف در برابر تغییر جریان مقاومت میکند. به همین دلیل، هنگامی که سوئیچها برای تغییر جریان فعال میشوند، سلف در برابر تغییر مقاومت نشان میدهد. از این رو شکل موج متفاوت خواهد بود.
این وضعیتها با توجه به اینکه ابتدا همه سوئیچها خاموش هستند و انرژی اجزای ذخیرهسازی صفر است مورد بحث قرار میگیرند.
وضعیت 1 ($$ 0< t < t _ 1 $$)
در این حالت، سوئیچ $$S_ 1 $$ از فاصله زمانی $$t_1$$ تا $$t_2$$ هدایت خواهد کرد. به محض روشن شدن $$ S_ 1 $$، جریان از منبع DC و در بار برقرار خواهد شد. جریان از ترمینال B وارد میشود و این نشان میدهد که ولتاژ B بزرگتر از A است. ولتاژ منبع روی بار ظاهر میشود که برابر با $$ v _ { dc } / 2 $$ است و جریان به تدریج از صفر به مقدار حداکثر افزایش مییابد. سلف انرژی را ذخیره میکند زیرا پلاریته جریان و ولتاژ یکسان است.
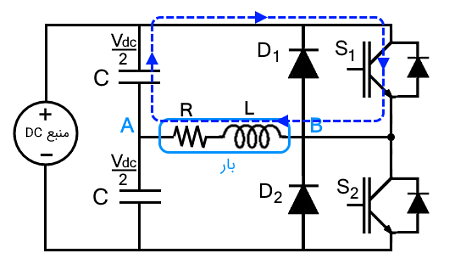
وضعیت 2 ($$t _ 1<t<t_2$$)
از آنجا که سوئیچ $$ S _ 1 $$ بسته است، ولتاژ منفی ($$-v _{dc}/2$$) روی بار ظاهر میشود، در حالی که جهت جریان همان جهت قبلی است، زیرا سلف در برابر تغییر مقاومت میکند. به عبارت دیگر، سلف انرژی ذخیره شده را تأمین میکند و $$D_2$$ مسیر جریان را از بار به منبع برقرار میکند. جریان بار به تدریج کاهش مییابد تا به صفر برسد. دلیل آن نیز عور جریان به دلیل انرژی ذخیره شده در سلف است. با تخلیه سلف، جریان گذرنده از بار صفر میشود.
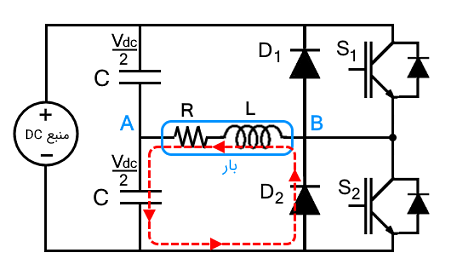
عامل اصلی در این حالت دیود فیدبک $$ D_ 2 $$ است که به عنوان دیود هرزگرد نیز شناخته میشود. این دیود دو کارکرد دارد: یکی فیدبک انرژی ذخیره شده از بار به منبع و دیگری کاهش ضربه پالسی $$ d i / d t $$ که ناشی از بار القایی است. عملکرد دیود هرزگرد $$ D _ 2 $$ با وضوح بیشتری در شکل بالا قابل مشاهده است.
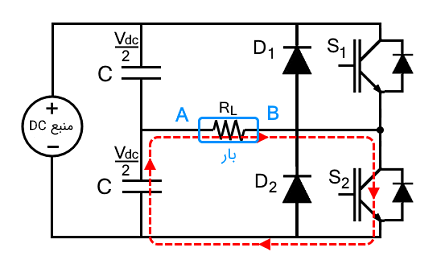
وضعیت 3 ($$t_ 2 < t < t _ 3 $$)
پس از تخلیه کامل سلف در بار، جریان بار صفر میشود. در اینجا، $$S_2$$ فعال و جهت جریان بار معکوس میشود. پس از فعال شدن $$ S _ 2 $$، جریان شروع به افزایش میکند و به پیک منفی میرسد. در این بازه، جریان و ولتاژ هر دو منفی هستند. بنابراین، سلف بار دیگر انرژی ذخیره میکند.
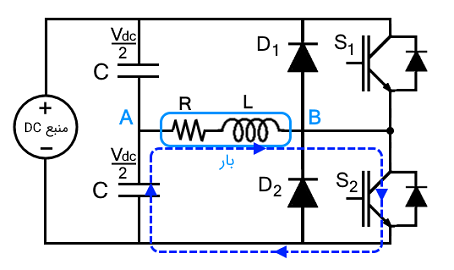
وضعیت 4 ($$t_3 < t < t _ 4$$)
در این فاصله زمانی سوئیچ $$ S _ 2 $$ خاموش است و ولتاژ مثبت ($$v _ { dc } / 2 $$) روی بار ظاهر میشود، در حالی که جهت جریان تغییری نمیکند. دیود $$D_ 1 $$ مسیر فیدبک انرژی ذخیره شده به بار را فراهم میکند. جریان بار به تدریج کاهش مییابد تا صفر شود. عملکرد دیود هرزگرد $$ D _ 1 $$ را میتوان در شکل زیر مشاهده کرد.
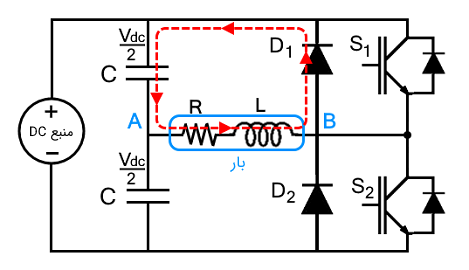
از آنجا که بار القایی خالص وجود ندارد (به دلیل مواردی چون مقاومت سیم و مقاومت مواد)، شکل موج مربوط به مدار RL را بررسی میکنیم که در ادامه نشان داده شده است.
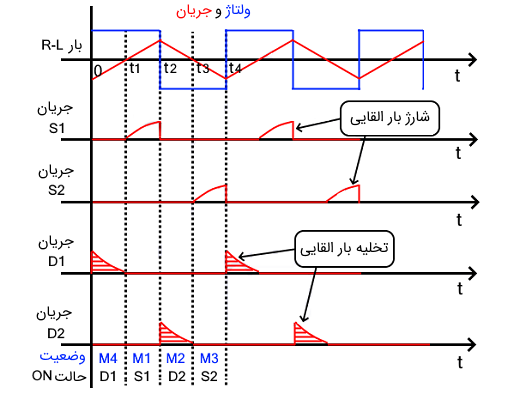
جریان لحظهای بار القایی خالص را میتوان با تقسیم ولتاژ خروجی بر امپدانس بار محاسبه کرد ($$Z = R + j n \omega L $$):
$$ \large i_L = \sum _ { n = 1 } ^ \infty \left ( \frac {v _{dc}} { n \pi \sqrt {R ^ 2 + (\omega L ) ^ 2}} \sin (n \omega t )\right ) $$
برای بار مقاومتی-سلفی جریان به صورت زیر به دست میآید:
$$ \large i_L = \sum _ { n = 1 } ^ \infty \left ( \frac {v _{dc}} { n \pi \sqrt {R ^ 2 + (\omega L ) ^ 2}} \sin (n \omega t -\theta _ n )\right ) $$
که در آن، $$ \theta _ n = \tan ^ {-1} (n\omega L/R)$$ است.
مقایسه شکل موج بارهای مختلف
عملکرد اینورتر نیم پل با بار RLC همانند عملکرد اینورتر برای بار RL است، البته با یک تفاوت کوچک. بنابراین، میتوان از شکل موج آنها این تمایز را تشخیص داد.
عملكرد و شكل موج به مقدار اندوکتانس و ظرفیت بار RLC بستگی دارد. کارکرد اینورتر نیم پل H با بار RLC مشابه بار RL است.
همانطور که میدانیم، در خازن جریان پیشفاز و ولتاژ پسفاز است و در سلف برعکس. بنابراین با دو بار RLC مواجهیم: بار RLC با سلف غالب و بار RLC با خازن غالب. حالت اول یعنی اندوکتانس بزرگتر از خازن است، در حالی که دومی به معنای بزرگتر بودن ظرفیت در بار RLC است.
بنابراین، اگر اندوکتانس در بار RLC غالب باشد، جریان بار نسبت به ولتاژ آن پسفاز خواهد بود. و اگر خازن در بار RLC غالب باشد، جریان نسبت به ولتاژ پیشفاز میشود.
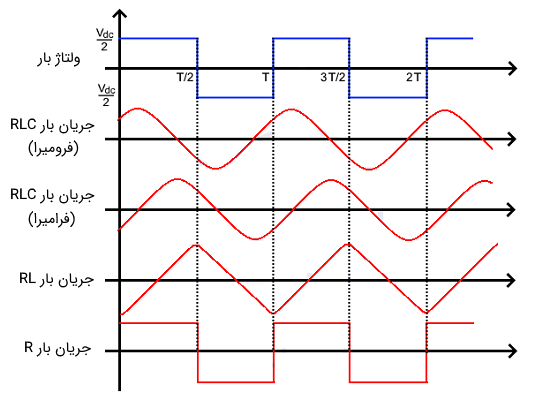
هنگامی که بار خازنی باشد (خازن غلبه کند)، عملکرد و شکل موج برای بار RLC متفاوت است. در بار RLC غالب خازنی، دیودهای فیدبک به دلیل تغییر در شکل موج جریان، در بازههای زمانی متفاوتی هدایت خواهند کرد.










