مساحت چند ضلعی منتظم چگونه بدست می آید؟ — به زبان ساده + حل مثال

مساحت چند ضلعی منتظم معمولا توسط رابطه «۲ ÷ (محیط × ارتفاع)» یا «A=aP/۲» به دست می‌آید. به دلیل برابر بودن اندازه تمام ضلع‌ها و زاویه‌های چندضلعی‌های منتظم، اغلب اجزای این اشکال هندسی به وسیله روابط مثلثاتی با هم در ارتباط هستند. به همین دلیل، فرمول‌های متعددی برای محاسبه مساحت چندضلعی‌های منتظم ارائه شده‌اند. البته مبنای اغلب این فرمول‌ها مشابه یکدیگر است. در این مقاله از مجله فرادرس، به معرفی فرمول‌های محاسبه مساحت چند ضلعی منتظم و اثبات برخی از آن‌ها می‌پردازیم. به علاوه، چندین مثال متنوع را نیز حل می‌کنیم.

چند ضلعی منتظم چیست؟

در مطالب قبلی از مجله فرادرس در مورد چند ضلعی‌ها و چند ضلعی‌های منتظم صحبت کردیم. به چند ضلعی که همه اضلاع و زاویه‌هایش برابر باشند، چندضلعی منتظم می‌گویند. چندضلعی‌های منتظم بر اساس تعداد ضلع‌هایشان به سه‌ضلعی منتظم (مثلث متساوی الاضلاع)، چهارضلعی منتظم (مربع)، پنج‌ضلعی منتظم، شش‌ضلعی منتظم و غیره تقسیم می‌شوند.

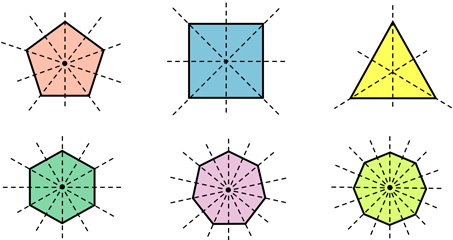
مساحت چند ضلعی منتظم چگونه بدست می‌آید؟

مساحت چند ضلعی منتظم با استفاده از محیط و ارتفاع به دست می‌آید. محیط، به عنوان اندازه دور چندضلعی منتظم تعریف می‌شود.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

ارتفاع نیز فاصله عمودی مرکز این شکل هندسی تا ضلع‌های آن است. تصویر زیر، محیط و ارتفاع‌های یکی از شناخته شده‌ترین چندضلعی ‌های منتظم را نمایش می‌دهد. این چند‌ضلعی، مربع نام دارد.

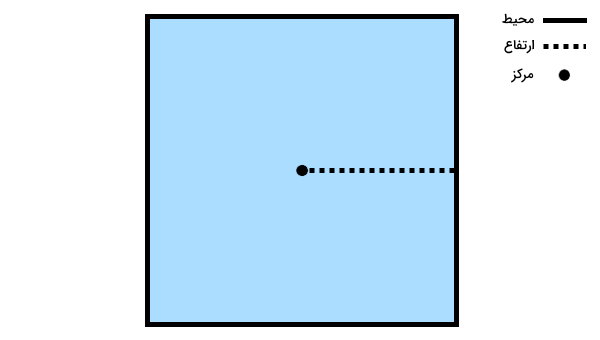
در صورت داشتن اندازه ارتفاع و محیط مربع، امکان محاسبه مساحت مربع با استفاده از فرمول زیر فراهم می‌شود:

۲ ÷ (محیط چند ضلعی × ارتفاع چند ضلعی) = مساحت چند ضلعی منتظم

البته، مربع یک حالت خاص از چندضلعی‌های منتظم است و فرمول مساحت مخصوص به خود را دارد. با این وجود، مساحت تمام چندضلعی‌های منتظم را می‌توان با استفاده از رابطه بالا به دست آورد.

عبارت جبری فرمول مساحت چند ضلعی منتظم

عبارت جبری فرمول مساحت چند ضلعی منتظم به صورت زیر نوشته می‌شود:

$$A = \frac { aP } { ۲ }$$

• A: مساحت چند ضلعی منتظم
• a: ارتفاع چند ضلعی منتظم
• P: محیط چند ضلعی منتظم

در بخش‌های بعدی، به منظور درک بهتر رابطه بالا، تعاریف و فرمول‌های مربوط به محیط و ارتفاع چند ضلعی منتظم را نیز مورد بررسی قرار خواهیم داد.

مثال ۱: محاسبه مساحت شش ضلعی منتظم

محیط یک شش‌ضلعی برابر با ۱۲۰ و اندازه ارتفاع آن برابر با ۸/۶۶ است. اگر اندازه تمام ضلع‌ها و زاویه‌های شش‌ضلعی برابر باشد، مساحت آن چقدر خواهد بود؟

در صورت برابر بودن اندازه تمام ضلع‌ها و زاویه‌ها، شش‌ضلعی مورد سوال، منتظم است. مساحت شش‌ضلعی منتظم، از فرمول زیر به دست می‌آید:

$$A = \frac { aP } { ۲ }$$

• A: مساحت شش‌ضلعی منتظم
• a: ارتفاع شش‌ضلعی برابر با ۸/۶۶
• P: محیط شش‌ضلعی برابر با ۱۲۰

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$A = \frac { ۸/۶۶ \times ۱۲۰ } { ۲ }$$

$$A = ۸/۶۶ \times ۶۰$$

$$A = ۵۱۹/۶$$

در نتیجه، مساحت شش‌ضلعی منتظم برابر با ۵۱۹/۶ واحد سطح است.

مثال ۲: محاسبه ارتفاع پنج ضلعی منتظم از روی محیط و مساحت

محیط و مساحت یک پنج‌ضلعی منتظم، به ترتیب برابر ۴۰ سانتی‌متر و ۱۱۰ سانتی‌متر مربع است. اندازه ارتفاع این پنج‌ضلعی را حساب کنید.

با توجه به اطلاعات مسئله، اندازه ارتفاع پنج‌ضلعی با استفاده از فرمول مساحت چند ضلعی منتظم محاسبه می‌شود:

$$A = \frac { aP } { ۲ }$$

• A: مساحت پنج‌منتظم برابر با ۱۱۰ سانتی‌متر مربع
• a: ارتفاع پنج‌ضلعی
• P: محیط پنج‌ضلعی برابر ۴۰ سانتی‌متر

اندازه‌های معلوم را درون فرمول قرار می‌دهیم و آن را بر حسب ارتفاع (a) حل می‌کنیم:

$$۱۱۰ = \frac { a \times ۴۰ } { ۲ }$$

$$a \times ۴۰ = ۱۱۰ \times ۲$$

$$a = \frac { ۱۱۰ \times ۲ } { ۴۰ }$$

$$a = \frac { ۲۲۰ } { ۴۰ }$$

$$a = ۵/۵$$

در نتیجه، ارتفاع چند ضلعی منتظم برابر با ۵/۵ سانتی‌متر است.

تعریف پارامترهای فرمول مساحت چند ضلعی منتظم

در بخش قبلی، یکی از روش‌های محاسبه مساحت چند ضلعی منتظم را معرفی کرده و چند مثال در رابطه با آن حل کردیم. در این بخش، پارامترهای مورد استفاده در فرمول مساحت چند ضلعی منتظم را به همراه فرمول‌های محاسبه آن‌ها را به طور دقیق مورد بررسی قرار می‌دهیم.

فیلم مجموعه آموزش دروس پایه دهم – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

محیط چند ضلعی منتظم چیست؟

«محیط» (Perimeter)، مجموع طول ضلع‌های تشکیل‌دهنده چندضلعی منتظم است. به دلیل برابر بودن طول تمام ضلع‌های چندضلعی منتظم، محیط این شکل از ضرب یک ضلع در تعداد کل ضلع‌ها به دست می‌آید. فرمول محیط چندضلعی منتظم عبارت است از:

$$P = sn$$

• P: محیط چند ضلعی منتظم
• s: طول ضلع چندضلعی منتظم
• n: تعداد ضلع‌های چندضلعی منتظم

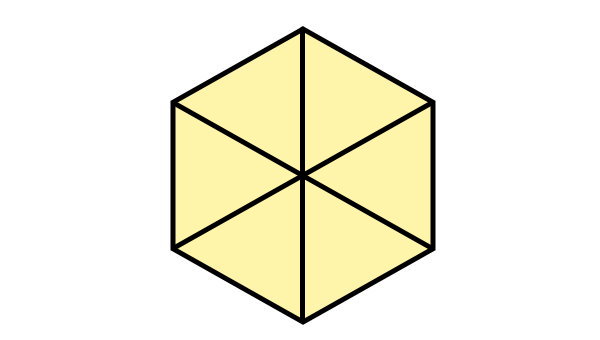
به عنوان مثال، شش‌ضلعی منتظم زیر را در نظر بگیرید.

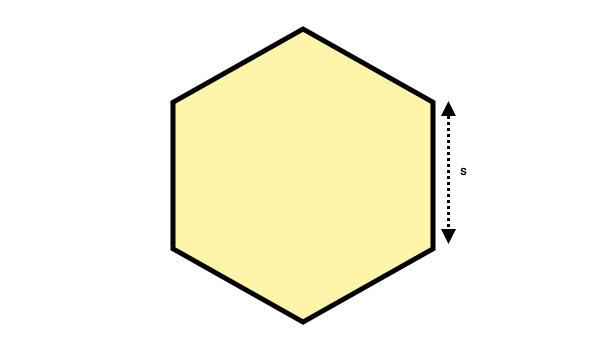
بر اساس رابطه محیط چندضلعی منتظم، محیط شش‌ضلعی بالا برابر است با:

$$P = ۶s$$

ارتفاع چند ضلعی منتظم چیست‌ ؟

به کوچک‌ترین فاصله نقاط روی محیط چند ضلعی منتظم تا مرکز آن، «ارتفاع» (Apothem) می‌گویند. یک چندضلعی منتظم، به تعداد ضلع‌هایش، ارتفاع دارد. این ارتفاع، با ضلع‌های چندضلعی منتظم، زاویه ۹۰ درجه می‌سازند. تصویر زیر، یکی از ارتفاع‌های یک شش‌ضلعی منتظم را نمایش می‌دهد.

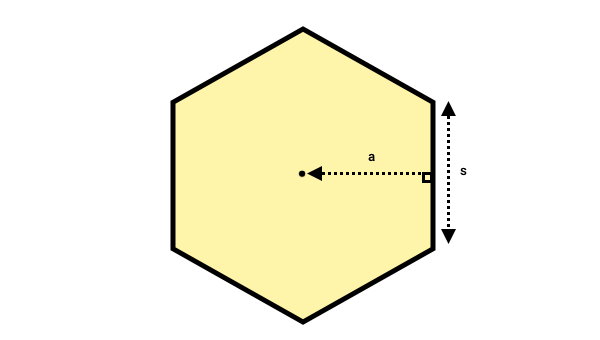
ارتفاع چندضلعی منتظم، با عنوان «شعاع دایره ی محاطی» (Inradius) نیز شناخته می‌شود. اگر دایره‌ای را درون یک چندضلعی منتظم محاط کنیم، شعاع آن با ارتفاع چندضلعی منتظم برابر می‌شود. محاسبه ارتفاع چندضلعی منتظم، پیچیده‌تر از محاسبه محیط آن است. فرمول ارتفاع چند ضلعی منتظم به صورت زیر نوشته می‌شود:

$$a = \frac { s } { ۲ \tan { (\frac { ۱۸۰ ^ { \circ } } { n } }) }$$

• a: ارتفاع چندضلعی منتظم
• s: طول ضلع چندضلعی منتظم
• n: تعداد ضلع‌های چندضلعی منتظم

رابطه بالا، بر اساس روابط مثلثاتی به دست می‌آید. بر اساس این روابط، تانژانت زاویه بین وتر و ساق مثلث قائم الزاویه، برابر با نسبت طول ضلع مقابل آن زاویه به ضلع مجاور آن زاویه است. اگر ارتفاع‌ها و قطرهای چندضلعی منتظم را رسم کنیم، چندضلعی منتظم به چند مثلث قائم الزاویه تقسیم می‌شود.

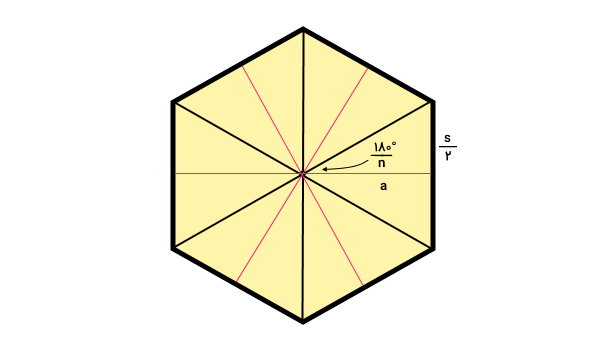
زاویه حول مرکز چندضلعی، یک زاویه کامل یا ۳۶۰ درجه است. با رسم ارتفاع‌ها و قطرهای یک n چندضلعی منتظم، ۲n مثلث قائم الزاویه به وجود می‌آید. بنابراین، زاویه راس این مثلث‌ها در مرکز چندضلعی برابر می‌شود با:

$$\frac { ۳۶۰ ^ { \circ } } { ۲n } = \frac { ۱۸۰ ^ { \circ } } { n }$$

ضلع مجاور به زاویه بالا برابر با a و ضلع مقابل آن برابر با s/۲ است. در نتیجه، تانژانت این زاویه از نسبت زیر به دست می‌آید:

$$\tan { ( \frac { ۱۸۰ ^ { \circ } } { n } ) } = \frac { \frac { s } { ۲ } } { a }$$

رابطه بالا را بر حسب ارتفاع (a) بازنویسی می‌کنیم:

$$a = \frac { \frac { s } { ۲ } } { \tan { ( \frac { ۱۸۰ ^ { \circ } } { n } ) } }$$

$$a = \frac { s } { ۲ \tan { ( \frac { ۱۸۰ ^ { \circ } } { n } ) } }$$

این رابطه، همان فرمول ارتفاع چندضلعی منتظم است که برای محاسبه مساحت چند ضلعی منتظم مورد استفاده قرار می‌گیرد.

مثال ۳: محاسبه مساحت چند ضلعی منتظم از روی ضلع

اندازه یک ضلع دوازده‌ضلعی منتظم برابر با ۱۵ متر است. مساحت این دوازده‌ضلعی را به دست بیاورید.

فرمول مساحت دوازده‌ضلعی منتظم برابر است با:

$$A = \frac { aP } { ۲ }$$

• A: مساحت دوازده‌ضلعی منتظم
• a: ارتفاع دوازده‌ضلعی
• P: محیط دوازده‌ضلعی

به منظور استفاده از فرمول بالا، باید اندازه محیط و ارتفاع را داشته باشیم. محیط، از رابطه زیر به دست می‌آید:

$$P = ns$$

• P: محیط منتظم
• n: تعداد ضلع‌ها برابر با ۱۲
• s: اندازه یک ضلع برابر با ۱۵ متر

$$P = ۱۲ \times ۱۵$$

$$P = ۱۸۰$$

محیط دوازده‌ضلعی برابر با ۱۸۰ متر است. فرمول محاسبه ارتفاع دوازده‌ضلعی به صورت زیر نوشته می‌شود:

$$a = \frac { s } { ۲ \tan { (\frac { ۱۸۰ ^ { \circ } } { n } }) }$$

• a: ارتفاع دوازده‌ضلعی
• s: اندازه ضلع برابر با ۱۵ متر
• n: تعداد ضلع‌ها برابر با ۱۲

$$a = \frac { ۱۵ } { ۲ \tan { (\frac { ۱۸۰ ^ { \circ } } { ۱۲ } }) }$$

$$a \approx ۲۷/۹۹$$

اکنون اندازه ارتفاع و محیط را داریم. در نتیجه می‌توانیم مساحت دوازده‌ضلعی را حساب کنیم:

$$A = \frac { ۲۷/۹۹ \times ۱۸۰} { ۲ }$$

$$A = \frac { ۵۰۳۸/۲ } { ۲ }$$

$$A = ۲۵۱۹/۱$$

در نتیجه، مساحت دوازده‌ضلعی منتظم برابر با ۲۵۱۹/۱ متر مربع است.

مثال ۴: محاسبه مساحت چندضلعی منتظم از روی زاویه خارجی

یکی از زوایای خارجی یک چندضلعی منتظم برابر با ۳۶ درجه، اندازه ارتفاع آن برابر با ۷ سانتی‌متر و اندازه ضلع آن برابر با ۴/۵۵ سانتی‌متر است. مساحت این چندضلعی منتظم را تعیین کنید.

با توجه به فرمول مساحت چندضلعی‌های منتظم، ابتدا محیط چندضلعی را به دست می‌آوریم:

$$P = ns$$

• P: محیط منتظم
• n: تعداد ضلع‌ها
• s: اندازه یک ضلع برابر با ۴/۵۵ سانتی‌متر

برای محاسبه محیط به تعداد ضلع‌های چندضلعی منتظم نیاز داریم. مجموع زوایای خارجی چندضلعی منتظم برابر با ۳۶۰ درجه است. به علاوه، تمام زوایای خارجی این نوع چندضلعی، اندازه برابر دارند. بنابراین، تعداد ضلع‌ها توسط رابطه زیر محاسبه می‌شود:

$$n = \frac { ۳۶۰ ^ { \circ } } { ۳۶ ^ { \circ } }$$

$$n = ۱۰$$

چندضلعی مورد سوال، یک ده‌ضلعی منتظم با محیط زیر است:

$$P = ۱۰ \times ۴/۵۵$$

$$P = ۴۵/۵۰$$

به این ترتیب، برای مساحت ده‌ضلعی منتظم داریم:

$$A = \frac { ۷ \times ۴۵/۵ } { ۲ }$$

$$A = \frac { ۳۱۸/۵} { ۲ }$$

$$A = ۱۵۹/۲۵$$

در نتیجه، مساحت ده‌ضلعی منتظم برابر با ۱۵۹/۲۵ سانتی‌متر مربع است.

اثبات فرمول مساحت چند ضلعی منتظم با مساحت مثلث

تمام چندضلعی‌های منتظم را می‌توان به مجموعه‌ای از مثلث‌های بهم‌پیوسته تقسیم کرد. به تقسیم‌بندی چندضلعی‌ها به چند مثلث، «مثلث بندی» (Triangulation) می‌گویند.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

روش‌های مختلفی برای مثلث‌بندی چندضلعی‌ها وجود دارد. در مثلث‌بندی چندضلعی‌های منتظم، معمولا مرکز شکل را به راس‌های آن متصل می‌کنند. به این ترتیب، n مثلث هم‌نهشت تشکیل می‌شود. n، تعداد ضلع‌های چندضلعی منتظم است.

هر ضلع چندضلعی منتظم، به عنوان قاعده یکی از مثلث‌ها در نظر گرفته می‌شود. از مرکز چندضلعی، ارتفاع هر مثلث را رسم می‌کنیم. قاعده مثلث را با حرف b و ارتفاع آن را با حرف h‌ نمایش می‌دهیم.

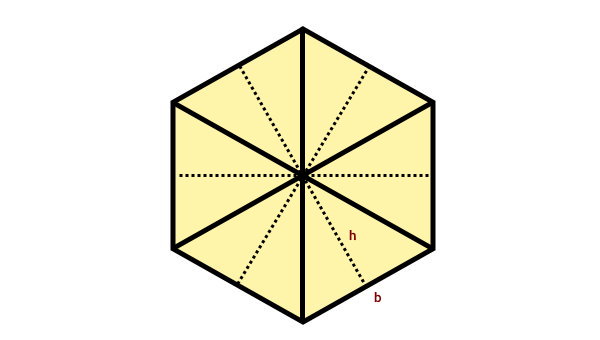
به دلیل هم‌نهشت بودن تمام مثلث‌ها، ارتفاع آن‌ها نیز با هم برابر است. مساحت چند ضلعی منتظم از جمع مساحت مثلث‌های تشکیل‌دهنده آن به دست می‌آید. مساحت مثلث با استفاده از فرمول زیر محاسبه می‌شود:

۲ ÷ (قاعده × ارتفاع) = مساحت مثلث

$$A = \frac { h \times b} { ۲ }$$

بر اساس رابطه بالا، مساحت یک n ضلعی منتظم (متشکل از n مثلث) از رابطه زیر به دست می‌آید:

$$A = \frac { n \times h \times b } { ۲ }$$

ارتفاع مثلث (h)، همان ارتفاع چندضلعی منتظم (a) و حاصل‌ضرب تعداد مثلث‌ها در قاعده (nb)، همان محیط چندضلعی منتظم (P) است. این عبارت‌های جبری معادل را درون رابطه بالا قرار می‌دهیم:

$$A = \frac { a \times P } { ۲ }$$

به این ترتیب، به فرمول مساحت چند ضلعی منتظم می‌رسیم.

مساحت چند ضلعی منتظم با دایره محاطی و محیطی

اگر یک دایره را به گونه‌ای درون یک چندضلعی منتظم رسم کنیم که تمام ضلع‌ها بر دایره مماس شوند، دایره را محاطی و چندضلعی را محیطی می‌نامیم.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در صورت رسم یک دایره گذرنده تمام راس‌های یک چندضلعی منتظم، دایره را محیطی و چندضلعی را محاطی می‌نامیم. تصویر زیر، یک پنج‌ضلعی منتظم با دایره‌های محاطی و محیطی آن را نمایش می‌دهد.

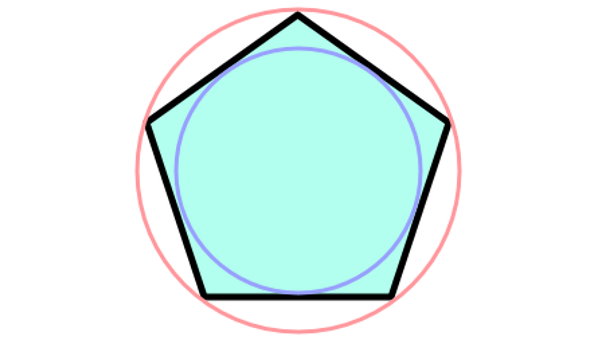
استفاده از دایره‌های محاطی و محاطی، یکی از روش‌های تعیین پارامترهای مورد نیاز برای محاسبه مساحت چند ضلعی منتظم است. دایره محاطی، شعاع‌های هم‌اندازه با ارتفاع چندضلعی منتظم دارد. بنابراین، پارامتر a در فرمول مساحت چند ضلعی منتظم را می‌توان به کمک این دایره به دست آورد.

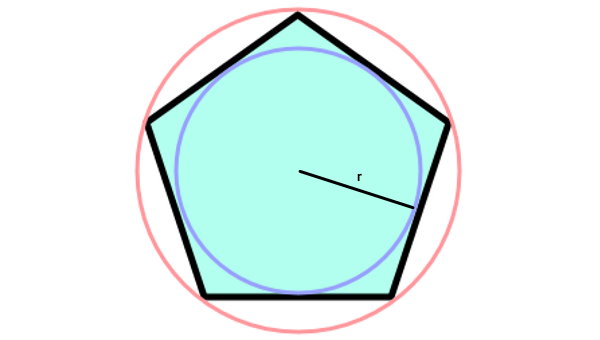
علاوه بر این، شعاع دایره محیطی، وتر مثلث قائم الزاویه‌ای است که طول یکی از ساق‌های آن، با نصف ضلع چندضلعی منتظم برابری می‌کند.

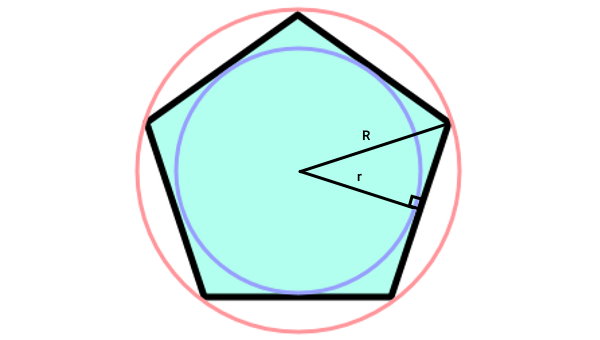
مطابق با قضیه فیثاغورس، رابطه زیر بین وتر و ساق‌های مثلث قائم الزاویه برقرار است:

$$c ^ { ۲ } = a ^ { ۲ } + b ^ { ۲ }$$

• c: وتر
• a: یکی از ساق‌ها
• b: ساق دیگر

اندازه ضلع چندضلعی منتظم را برابر با s در نظر می‌گیریم. به این ترتیب، اندازه یکی از ساق‌های مثلث قائم الزاویه بالا برابر با s/۲ خواهد بود.

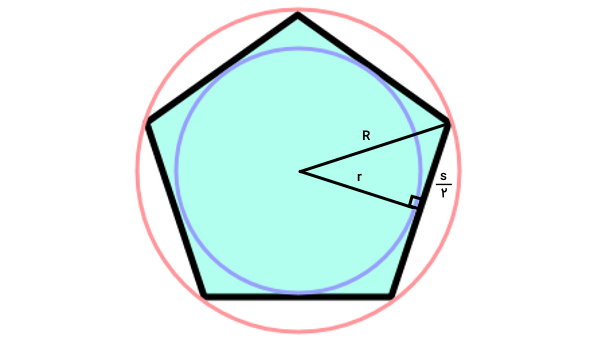
رابطه فیثاغورس را برای مثلث قائم الزاویه بالا می‌نویسیم:

$$R ^ { ۲ } = r ^ { ۲ } + ( \frac { s } { ۲ } ) ^ { ۲ }$$

• R: شعاع دایره محیطی
• r: شعاع دایره محاطی (ارتفاع چندضلعی منتظم)
• s: اندازه ضلع

با استفاده از فرمول بالا، در صورت داشتن اندازه شعاع دایره محیطی و شعاع دایره محاطی، می‌توانیم اندازه ضلع چندضلعی منتظم و سپس مساحت آن را به دست بیاوریم.

مثال ۵: محاسبه مساحت چند ضلعی منتظم محیطی

یک هفت‌ضلعی منتظم محیطی به ضلع ۱۸/۳ را در نظر بگیرید. اگر شعاع دایره محاطی این چندضلعی برابر با ۱۹ باشد، مساحت آن چقدر است؟

شعاع دایره محاطی چندضلعی محیطی، با ارتفاع آن برابر است. بنابراین، مساحت هفت‌ضلعی منتظم توسط فرمول زیر محاسبه می‌شود:

$$A = \frac { aP } { ۲ }$$

• A: مساحت هفت‌ضلعی منتظم
• a: ارتفاع هفت‌ضلعی برابر با ۱۹ (شعاع دایره محاطی)
• P: محیط هفت‌ضلعی منتظم

اندازه محیط هفت‌ضلعی منتظم را به طور مستقیم نداریم. این اندازه از ضرب تعداد ضلع‌ها (۷) در اندازه یک ضلع (۱۸/۳) به دست می‌آید:

$$P = ns$$

$$P = ۷ \times ۱۸/۳$$

$$P = ۱۲۸۱/۱$$

اندازه محیط را به همراه اندازه شعاع دایره محاطی در فرمول مساحت قرار می‌دهیم:

$$A = \frac { ۱۹ \times ۱۲۸۱/۱ } { ۲ }$$

$$A = \frac { ۲۴۳۴۰/۹ } { ۲ }$$

$$A = ۱۲۱۷/۴۵$$

در نتیجه، مساحت هفت‌ضلعی منتظم برابر با ۱۲۱۷/۴۵ واحد سطح است.

روابط مثلثاتی شعاع دایره محاطی و شعاع دایره محیطی

بین شعاع‌های دایره‌های محاطی و محیطی و اندازه ضلع چندضلعی منتظم، روابط مثلثاتی زیر برقرار است:

$$\begin{aligned} s & = ۲ r \tan \left ( \frac { \pi }{ n }\right ) \\ &=۲ R \sin \left( \frac{ \pi }{ n }\right ) \\ r &= \frac{ ۱ }{ ۲ } s \cot \left( \frac{ \pi }{ n }\right) \\ &=R \cos \left( \frac{ \pi }{ n }\right) \\ R &=\frac{ ۱ }{ ۲ } s \csc \left( \frac{ \pi }{ n }\right) \\ &=r \sec \left( \frac{ \pi }{ n } \right) \end{aligned}$$

بر اساس این روابط، فرمول مساحت چند ضلعی منتظم به شکل‌های زیر در می‌آید:

$$\begin{aligned} A &=\frac{ ۱ }{ ۴ } n a^{ ۲ } \cot \left( \frac{ \pi }{ n } \right ) \\ &=n r^{ ۲ } \tan \left( \frac{ \pi }{ n } \right ) \\ &=\frac{ ۱ }{ ۲ } n R^{۲} \sin \left( \frac{ ۲ \pi }{ n } \right ) \end{aligned}$$

مثال ۶: محاسبه مساحت چند ضلعی منتظم محاطی

شعاع دایره محیطی یک نه‌ضلعی منتظم برابر با ۳۰ است. مساحت نه‌ضلعی را حساب کنید.

به منظور تعیین مساحت نه‌ضلعی منتظم، به اندازه ضلع و ارتفاع آن نیاز داریم. هر دوی این اندازه‌ها به وسیله شعاع دایره محیطی قابل محاسبه هستند. بر اساس روابط مثلثاتی موجود، اندازه هر ضلع چندضلعی منتظم برابر است با:

$$s = ۲ R \sin { (\frac{ \pi }{ n }) }$$

• s: اندازه ضلع
• R: شعاع دایره محیطی برابر ۳۰
• n: تعداد ضلع‌ها برابر ۹

$$s = ۲ \times ۳۰ \times \sin { (\frac{ \pi }{ ۹ }) }$$

$$s = ۲ \times ۳۰ \times ۰/۳۴۲$$

$$s = ۲۰/۵۲$$

اکنون می‌توانیم با استفاده از قضیه فیثاغورس، ارتفاع نه‌ضلعی را نیز تعیین کنیم:

$$R ^ { ۲ } = r ^ { ۲ } + ( \frac { s } { ۲ } ) ^ { ۲ }$$

• R: شعاع دایره محیطی برابر با ۳۰
• r: شعاع دایره محاطی یا ارتفاع چندضلعی منتظم
• s: اندازه ضلع برابر با ۲۰/۵۲

$$۳۰ ^ { ۲ } = r ^ { ۲ } + ( \frac { ۲۰/۵۲ } { ۲ } ) ^ { ۲ }$$

$$۳۰ ^ { ۲ } = r ^ { ۲ } + ( ۱۰/۲۶ ) ^ { ۲ }$$

$$۹۰۰ = r ^ { ۲ } + ۱۰۵/۲۷$$

$$r ^ { ۲ } = ۹۰۰ - ۱۰۵/۲۷$$

$$r ^ { ۲ } = ۷۹۴/۷۳$$

$$r = ۲۸/۱۹$$

اکنون شعاع دایره محاطی یا همان ارتفاع نه‌ضلعی منتظم و اندازه ضلع آن را داریم. به این ترتیب، مساحت نه‌ضلعی را محاسبه می‌کنیم:

$$A = \frac { aP } { ۲ }$$

• A: مساحت هفت‌ضلعی منتظم
• a: ارتفاع نه‌ضلعی برابر با ۲۸/۱۹
• P: محیط نه‌ضلعی برابر با ۱۸۴/۶۸=۲۰/۵۲ × ۹

$$A = \frac { ۲۸/۱۹ \times ۱۸۴/۶۸ } { ۲ }$$

$$A = \frac { ۵۲۰۶/۱۳ } { ۲ }$$

$$A \approx ۲۶۰۳$$

در نتیجه، مساحت نه‌ضلعی منتظم، تقریبا برابر با ۲۶۰۳ واحد سطح است.

جدول فرمول های مساحت چند ضلعی منتظم

در بخش‌های قبلی، رایج‌ترین فرمول محاسبه مساحت چند ضلعی های منتظم را معرفی و اثبات کردیم. روش‌های متعددی برای نوشتن این فرمول وجود دارد.

فیلم مجموعه آموزش دروس پایه یازدهم – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

جدول زیر، برخی از فرم‌های ریاضی مساحت چند ضلعی منتظم را نمایش می‌دهد.

محاسبه آنلاین مساحت چند ضلعی منتظم

محاسبه‌گرهای آنلاین متعددی برای تعیین مساحت انواع چندضلعی‌های منتظم وجود دارند. از بهترین ابزارهای محاسبه آنلاین مساحت چند ضلعی منتظم می‌توان به سایت Omni Calculator، سایت Calculator Soup (+) و سایت Keisan (+) اشاره کرد. به منظور آشنایی با نحوه به کارگیری این ابزارها، ماشین‌حساب سایت Omni Calculator را مورد بررسی قرار می‌دهیم.

محاسبه آنلاین مساحت چندضلعی منتظم با Omni Calculator

سایت Omni Calculator (+)، دو ماشین‌حساب مخصوص برای محاسبه مساحت چندضلعی‌های منتظم دارد. با وارد کردن تعداد ضلع‌ها و اندازه یک ضلع در ماشین‌حساب ساده این سایت (+)، شعاع دایره محاطی (ارتفاع چندضلعی منتظم)، شعاع دایره محیطی و مساحت چندضلعی منتظم محاسبه می‌شوند.

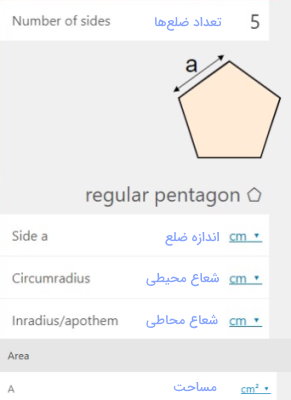
علاوه بر این ماشین‌حساب، Omni Calculator، یک ابزار محاسباتی دیگر نیز برای محاسبه مساحت چندضلعی منتظم دارد. البته این ابزار (+)، امکان محاسبه محیط، شعاع دایره محاطی، شعاع دایره محیطی، زاویه داخلی و زاویه مرکزی مقابل هر ضلع را نیز فراهم می‌کند.

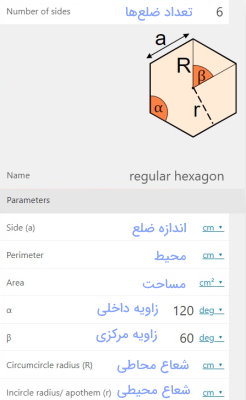
به عنوان مثال، برای به دست آوردن اندازه‌های یک هشت‌ضلعی به ضلع ۱۷ سانتی‌متر، عدد ۸ را درون کادر مقابل عنوان «Number of sides» و عدد ۱۷ را درون کادر مقابل «Side a» وارد می‌کنیم. به علاوه، یکاها را بر روی گزینه‌های متناسب (سانتی‌متر و سانتی‌متر مربع) قرار می‌دهیم. به این ترتیب، مساحت و دیگر اندازه‌های چندضلعی منتظم محاسبه می‌شوند و در مقابل کادر مربوط به آن‌ها به نمایش در می‌آیند.

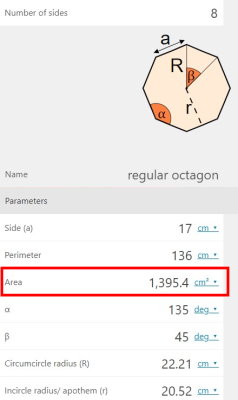
بر اساس خروجی نمایش داده شده در تصویر بالا، مساحت هشت‌ضلعی به ضلع ۱۷ سانتی‌متر، برابر با ۱۳۹۵/۴ سانتی‌متر مربع است.

مساحت چند ضلعی غیر منتظم

چندضلعی غیر منتظم، یکی از انواع چندضلعی‌ها است که تمام ضلع‌ها و زاویه‌های آن مساوی نیستند. مستطیل، لوزی، مثلث متساوی‌الساقین، مثلث قائم الزاویه، ذوزنقه، متوازی‌الاضلاع و بسیاری از شکل‌های هندسی، در گروه چندضلعی‌های غیر منتظم قرار می‌گیرند. برخلاف چندضلعی‌های منتظم، روش‌ها و فرمول‌های محاسبه مساحت چندضلعی‌های غیر منتظم، معمولا با یکدیگر تفاوت دارند. به همین دلیل، معمولا برای هر یک از آن‌ها، فرمول‌های جداگانه‌ای ارائه می‌شود.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

به عنوان مثال، فرمول محاسبه مساحت مستطیل، «طول × عرض» و فرمول محاسبه مساحت لوزی، «۲ ÷ (قطر کوچک × قطر بزرگ)» است. البته تمام چندضلعی‌ها را می‌توان به مجموعه‌ای از چندین مثلث تقسیم کرد. بنابراین، مشابه مساحت چندضلعی‌های منتظم، امکان محاسبه مساحت چندضلعی‌های غیر منتظم با روش مثلث بندی وجود دارد.

سوالات متداول در رابطه با مساحت چند ضلعی منتظم

در این مطلب از مجله فرادرس در مورد چند ضلعی منتظم و مساحت آن‌ها صحبت کردیم. در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت چندضلعی‌های منتظم به طور خلاصه پاسخ می‌دهیم.

تعریف مساحت چندضلعی منتظم چیست؟

مساحت چندضلعی‌های منتظم، سطح درون ضلع‌های این اشکال هندسی است.

مساحت چندضلعی منتظم چگونه محاسبه می‌شود؟

مساحت چندضلعی منتظم، معمولا با استفاده از اندازه ارتفاع و مجموع طول ضلع‌های آن محاسبه می‌شود.

فرمول مساحت چندضلعی منتظم چیست؟

فرمول مساحت چندضلعی منتظم، «A=aP/۲» است. a، ارتفاع و P، محیط را نمایش می‌دهد.

آیا امکان محاسبه مساحت چندضلعی منتظم بدون ارتفاع وجود دارد؟

بله. در چندضلعی‌های منتظم، تمام اجزا به وسیله روابط مثلثاتی با هم در ارتباط هستند. بنابراین، امکان محاسبه مساحت با ضلع یا حتی شعاع دایره محیطی نیز وجود دارد.