قضیه نیمساز زاویه – به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با روش‌های رسم نیمساز زاویه آشنا شدیم. در این آموزش، درباره قضیه نیمساز بحث می‌کنیم. با کمک قضیه نیمساز زاویه می‌توانیم طول اضلاع نامعلوم مثلث‌ها را بیابیم، زیرا یک نیمساز زاویه، ضلع مقابلش را به دو بخش تقسیم می‌کند که متناسب با دو ضلع دیگر مثلث هستند.

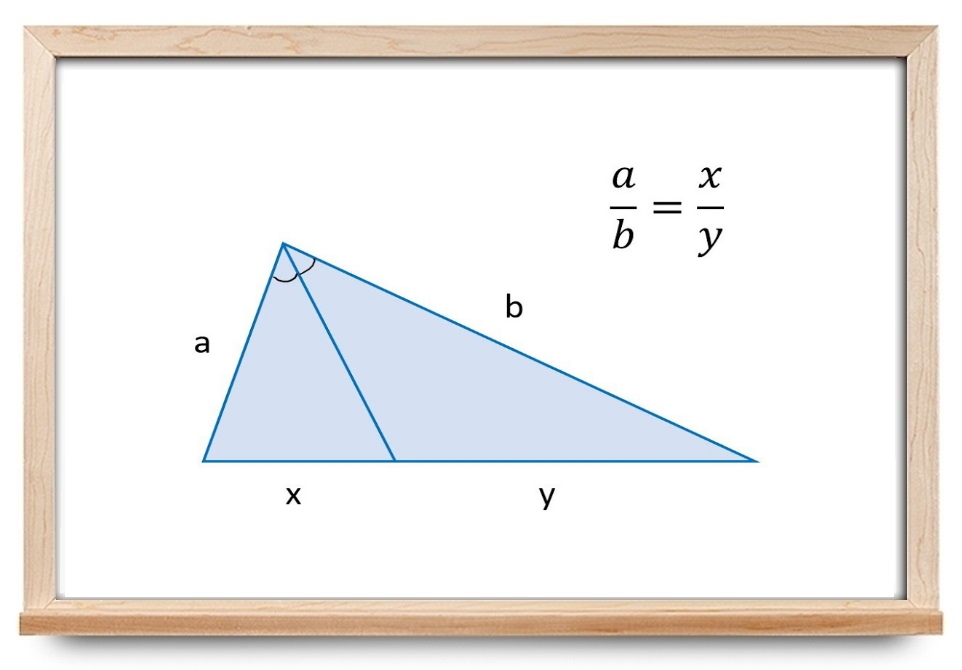
نیمساز زاویه

فرض کنید مثلث دلخواه $$ABC$$ داده شده است. زوایای داخلی $$A$$، $$B$$ و $$C$$ به ترتیب در مقابل اضلاع $$a$$، $$b$$ و $$c$$ قرار دارند. اگر خطی از رأس $$A$$ رسم کنیم، به گونه‌ای که $$\angle A$$ را به دو زاویه مساوی تقسیم کرده و با ضلع $$a$$ تقاطع داشته باشد، این خط را نیمساز زاویه مثلث می‌نامیم.

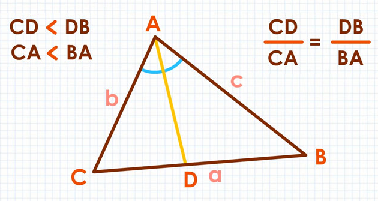
مثلث شکل زیر را در نظر بگیرید. خط $$AD$$ نیمساز زاویه $$A$$ است که ضلع مقابلش، یعنی $$a$$، را به دو قسمت $$CD$$ و $$DB$$ تقسیم کرده است.

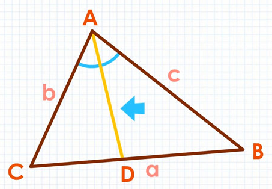
قضیه نیمساز زاویه داخلی مثلث

قضیه نیمساز زاویه بیان می‌کند که یک نیمساز زاویه در مثلث، ضلع مقابل آن را به دو بخش تقسیم می‌کند که متناسب با دو ضلع دیگر مثلث هستند.

فیلم آموزش هندسه ۳ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در مثلث شکل بالا، نیمساز $$AD$$ ضلع $$a$$ را به دو بخش $$CD$$ و $$DB$$ تقسیم می‌کند. طبق قضیه نیمساز زاویه، این دو بخش متناسب با اضلاع $$b$$ ($$CA$$) و $$c$$ ($$BA$$) هستند.

نیمساز زاویه مثلث را به دو مثلث $$ACD$$ و $$ABD$$ تقسیم می‌کند.

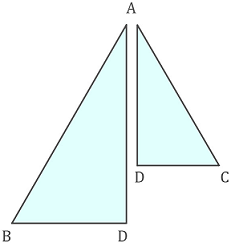
به عبارت دیگر، طبق قضیه نیمساز می‌توان نوشت:

$$\large \frac {CD}{DB} = \frac {CA} { B A }$$

قضیه نیمساز زاویه خارجی مثلث

در آموزش‌های قبلی، با زاویه خارجی در چندضلعی‌ها آشنا شدیم و دیدیم که اگر یکی از اضلاع مثلث را به صورت خط راست ادامه دهیم، زاویه‌ای که بین این امتداد و ضلع کناری آن تشکیل می‌شود، «زاویه خارجی» (Exterior Angle) نام دارد.

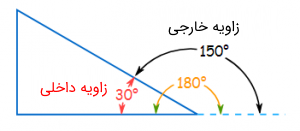
قضیه نیمساز زاویه خارجی بیان می‌کند که یک نیمساز زاویه خارجی در مثلث، ضلع خارجی مقابلش را به دو بخش تقسیم می‌کند که متناسب با دو ضلع دیگر مثلث هستند.

مثلث زیر را در نظر بگیرید که $$AD'$$ نیمساز زاویه خارجی $$A$$ است.

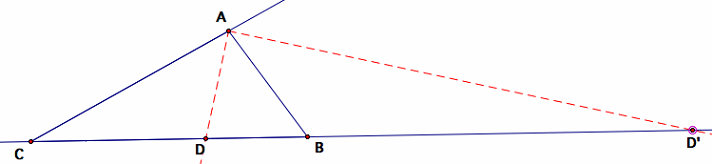
طبق قضیه نیمساز زاویه خارجی، می‌توان نوشت:

$$\large \frac { A C } { A B } = \frac {D' C } {D' B }$$

مثال‌ها

در این بخش، چند مثال را از کاربرد قضیه نیمساز بیان می‌کنیم.

مثال ۱

مثلث زیر را در نظر بگیرید. آیا خط $$AD$$ نیمساز زاویه $$A$$ است؟

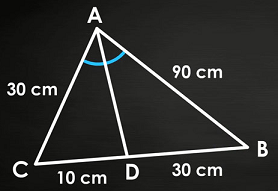
حل: نسبت اضلاع و دو بخش ضلع مقابل خط $$AD$$ را می‌نویسیم. اگر خط $$AD$$ نیمساز زاویه $$A$$ باشد، باید طبق قضیه نیمساز رابطه زیر را داشته باشیم:

$$\large \frac { CD}{DB} = \frac {CA} { B A }$$

با توجه به اندازه اضلاع مثلث بالا، داریم:‌

$$\large \frac {10}{30} = \frac {30}{90}$$

از آنجایی که تساوی مربوطه برقرار است، می‌توان گفت که خط $$A D$$ نیمساز زاویه $$A$$ است.

فیلم اثبات قضیه نیمسازها هندسه (یازدهم) + مثال (فیلم آموزش رایگان) در فرادرس

کلیک کنید

مثال ۲

در مثلث شکل زیر، خط $$A D$$ نیمساز زاویه $$A$$ است. اندازه ضلع $$B A$$ را به دست آورید.

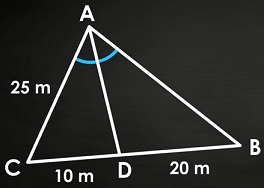
حل: اگر خط $$AD$$ نیمساز زاویه $$A$$ باشد، باید تساوی زیر را داشته باشیم:

$$\large \frac { CD}{DB} = \frac {CA} { B A }$$

با توجه به اطلاعات مثال، داریم:

$$\large \frac {10}{25} = \frac {20} { BA}$$

$$\large BA = \frac {500}{10}$$

$$\large B A = 50 \; \text{m}$$

مثال ۳

در مثلث $$\triangle { A B C }$$، داریم:

$$\large \lvert \overline { A B } \rvert = 1 0 ,\;\;\; \lvert \overline { B C } \rvert = 8 , \;\;\; \lvert \overline { A C } \rvert = 1 2$$

فرض کنید $$D$$ نقطه‌ای روی ضلع $$\overline { A B }$$ است، به گونه‌ای که خط $$\overline { C D }$$ نیمساز $$\angle C$$ باشد. طول $$\overline { A D }$$ را محاسبه کنید.

حل: فرض می‌کنیم:

$$\large \lvert \overline { A B } \rvert = c , \;\;\; \lvert \overline { B C } \rvert = a , \;\;\; \lvert \overline { A C } \rvert = b , \;\;\; \lvert\overline{AD}\rvert=y, \;\;\; \lvert\overline { B D } \rvert = x$$

بنابراین، باید $$y$$ را پیدا کنیم. طبق قضیه نیمساز زاویه، داریم:‌

$$\large \frac { y } { b } = \frac { x } { a } \implies \frac { y } { 1 2 } = \frac { x } { 8 } .$$

از آنجایی که $$x + y = c$$ یا $$x = c - y$$، می‌توان نوشت:‌

$$\large \begin {aligned} \frac { y } { 1 2 } & = \frac { 1 0 - y } { 8 } \\ \\ \Rightarrow y & = 6 . \ \end{aligned}$$

مثال ۴

مثلثی را در نظر بگیرید که یکی از رأس‌های آن با ارتفاع، میانه و نیمساز زاویه آن رأس به چهار زاویه مساوی تقسیم شده است. اندازه زاویه رأس مورد نظر را بیابید.

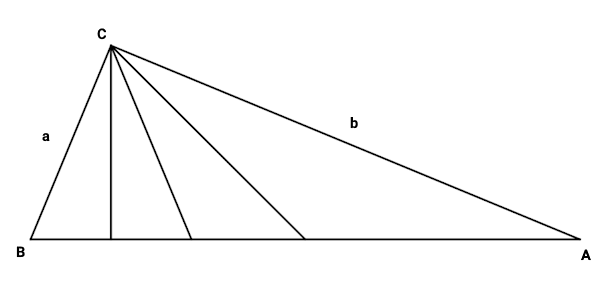
در این مثال، یک مثلث داریم که زاویه یکی از راس‌های آن (زاویه راس $$C$$) به چهار قسمت مساوی تقسیم شده است. تقسیم‌بندی زاویه مذکور توسط سه پاره‌خط صورت گرفته است. یکی از این پاره‌خط‌ها ارتفاع مثلث (پاره‌خط عمود بر قاعده مثلث)، دومین پاره‌خط نیم‌ساز زاویه راس مورد سوال (پاره‌خط نصف‌کننده زاویه راس) و پاره‌خط سوم، میانه مثلث (پاره‌خط رسم شده تا وسط قاعده) محسوب می‌شود. با استفاده از این اطلاعات، می‌خواهیم اندازه زاویه راس مورد سوال را به دست بیاوریم. به این منظور، مراحل زیر را طی می‌کنیم.

پاره‌خط‌های رسم شده، مثلث اصلی را به ۴ مثلث کوچک‌تر تقسیم می‌کنند. این مثلث‌ها را از چپ به راست، مثلث ۱، ۲، ۳ و ۴ در نظر بگیرید. مثلث ۱ و ۲، بر اساس حالت دو زاویه و یک ضلع در هم‌نهشتی مثلث‌ها، با یکدیگر برابر هستند؛ زیرا دو زاویه برابر (زاویه قائمه و زاویه راس حاصل از تقسیم‌بندی زاویه راس مثلث اصلی) و یک ضلع برابر (ضلع مشترک) دارند. بنابراین، اندازه تمام اجزای این دو مثلث با هم برابر است. از این رو، قاعده این دو مثلث را برابر با متغیری مانند $$x$$ در نظر می‌گیریم.

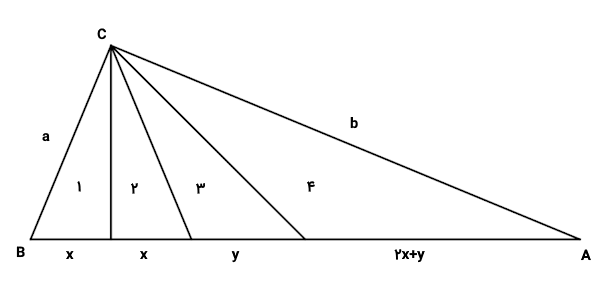
قاعده مثلث مثلث ۳ را برابر با متغیری مانند $$y$$ در نظر می‌گیریم. با توجه به شکل می‌توان مشاهده کرد که پاره‌خط سوم، میانه قاعده مثلث اصلی است. بنابراین، قاعده مثلث ۴ با قاعده مثلث‌های ۱ تا ۳ برابر است. بنابراین می‌توانیم اندازه قاعده مثلث ۴ را به صورت $$x + x + y$$ یا $$2 x+ y$$ بنویسیم. به این ترتیب، برای نسبت قاعده‌های هر چهار مثلث داریم:

$$x : x : y : 2 x + y$$

اکنون، اندازه ضلع سمت چپ مثلث بزرگ را برابر با $$a = 1$$ و اندازه ضلع سمت راست مثلث را برابر با متغیری به نام $$b$$ در نظر بگیرید. به دلیل مشابه بودن مثلث‌های ۱ و ۲، اندازه وتر مثلث ۲ نیز برابر با ۱ می‌شود.

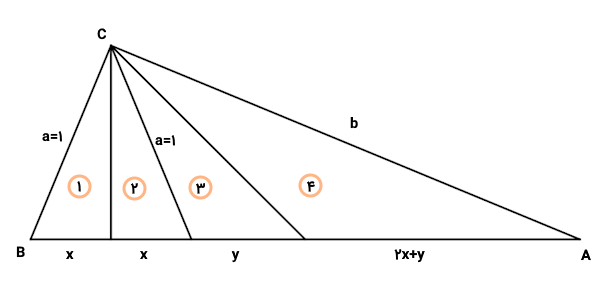
با این فرضیات، به سراغ قضیه نیمساز مثلث‌ها می‌رویم. این قضیه را ابتدا برای مثلث اصلی در نظر می‌گیریم (پاره‌خط‌های اول و سوم را در ذهن خود حذف کنید).

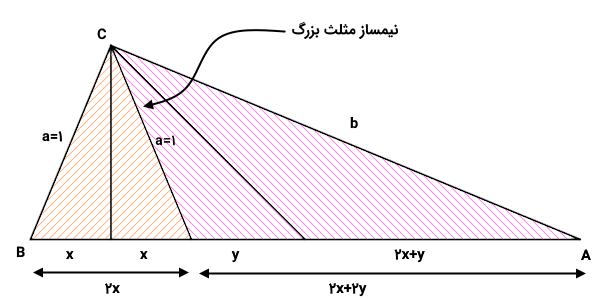
به این ترتیب، داریم:

$$\frac { 2 x + 2 y } { 2 x } = \frac { b } { a }$$

$$a$$ را برابر با ۱ در نظر گرفته بودیم. بنابراین:

$$b = \frac { 2 x + 2 y } { 2 x } = 1 + \frac { y } { x }$$

اکنون قضیه نیمساز مثلث‌ها را برای نیمه سمت راست مثلث اصلی (مثلث‌های ۳ و ۴) اعمال می‌کنیم.

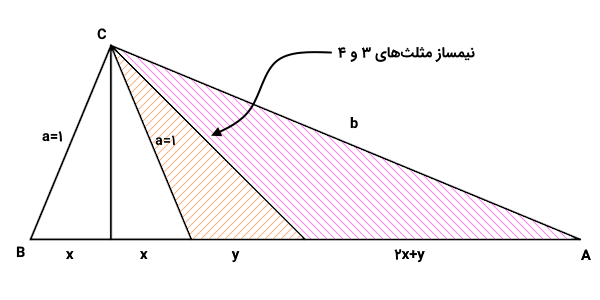
به این ترتیب، داریم:

$$\frac { 2 x + y } { y } = \frac { b } { a }$$

$$\frac { 2 x + y } { y } = \frac { b } { 1 }$$

$$b = \frac { 2 x } { y } + 1$$

اکنون، $$b$$های بدست‌آمده را برابر با یکدیگر قرار می‌دهیم:

$$1 + \frac { y } { x } = \frac { 2 x } { y } + 1$$

$$\frac { y } { x } = \frac { 2 x } { y }$$

از این رابطه می‌توانیم نتیجه زیر را به دست بیاوریم:

$$2 x ^ 2 = y ^ 2$$

$$y = x \sqrt { 2 }$$

به عبارت دیگر، نسبت $$x$$ به $$y$$ برابر است با:

$$x : y = 1 : \sqrt { 2 }$$

در مرحله بعد، قضیه نیمساز را برای دو مثلث کوچک‌تر در مرکز مثلث اصلی (مثلث‌های ۲ و ۳) در نظر می‌گیرم.

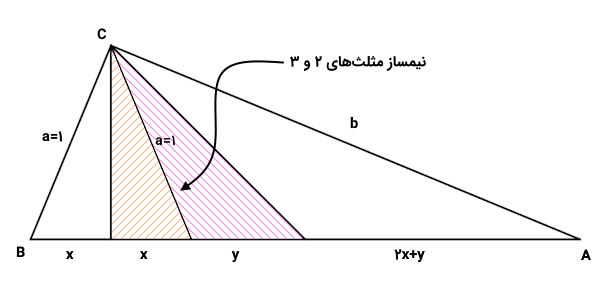
این دو مثلث، یک مثلث قائم‌الزاویه را تشکیل می‌دهند که با توجه قضیه نیمساز، نسبت ضلع قائمه به وتر آن برابر است با:

$$\frac { x } { y } = \frac { 1 } { \sqrt { 2 } }$$

ارتفاع و میانه مثلث قائم‌الزاویه، نسبت‌های برابر می‌سازند. بنابراین، با توجه به ویژگی‌های مثلث قائم‌الزاویه، این مثلث باید دارای دو زاویه ۴۵ درجه باشد. البته با استفاده از روابط نسبت‌های مثلثاتی، سینوس معکوس و مجموع زوایای داخلی مثلث نیز می‌توانستیم به همین نتیجه برسیم.

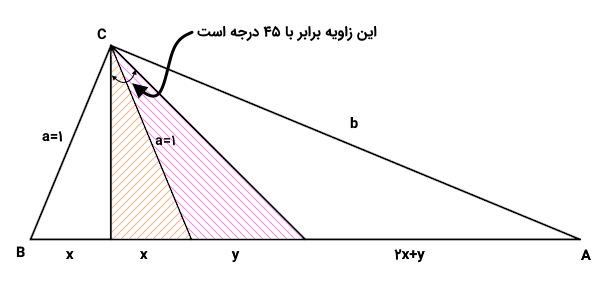
پاره‌خط میانی مثلث بالا، نیمساز آن است. بنابراین، هر یک از زاویه‌ها دو مثلث کوچک‌تر (مثلث‌های ۲ و ۳) در راس $$C$$ برابر با ۲۲/۵ درجه خواهد بود. به دلیل برابر بودن تمام زاویه‌های ساخته شده در راس C، اندازه این زاویه‌ها برابر با ۲۲/۵ درجه است.

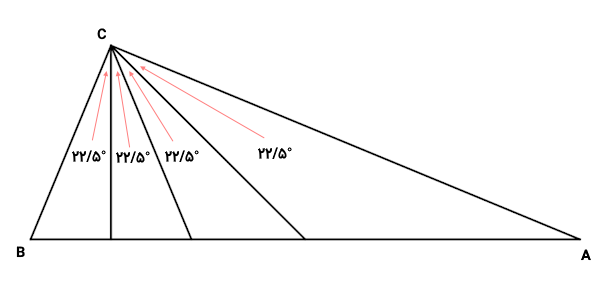
زاویه راس $$C$$ از جمع زوایای نمایش داده شده در تصویر بالا به دست می‌آید:

$$\angle { C } = 22.5 ^ { \circ } + 22.5 ^ { \circ } + 22.5 ^ { \circ } + 22.5 ^ { \circ } = 90 ^ { \circ }$$

در نتیجه، زاویه راس $$C$$ برابر با ۹۰ درجه است. به عبارت دیگر، مثلث مورد سوال، یک مثلث قائم‌الزاویه است.