قانون هوک — به زبان ساده

زمانی که وارد جایی می‌شوید و در بعد از باز شدن آرام بسته می‌شود، فنرها وارد عمل شده‌اند. بسیاری از وسیله‌های ورزشی نیز که برای قوی شدن عضلات خود استفاده می‌کنید از فنر استفاده می‌کنند. به صورت کلی باید گفت فنرها کاربرد زیادی در زندگی روزمره انسان دارند. اولین بار فیزیکدان انگلیسی «رابرت هوک» رفتار فنر را بررسی کرد، به همین دلیل نام این فیزیکدان با فنر عجین شده است و عموم فیزیکدانان قانون فنر را به عنوان قانون هوک می‌شناسند. در این آموزش قوانین حاکم بر فنرها را بررسی خواهیم کرد.

نیروی فنر

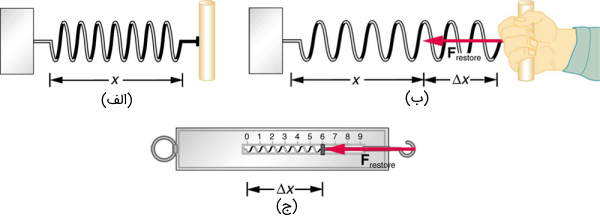
اگر نیرویی سبب شود که فنری به اندازه $$x$$ از نقطه تعادل خود جابه‌جا شود، فنر در مخالفت با نیروی وارد شده نیرویی خلاف جهت جابه‌جایی خود وارد می‌کند تا دوباره به حالت تعادل بازگردد. بیان ریاضی قانون هوک به صورت زیر نوشته می‌شود:

$$\large F=-kx$$‌

فیلم آموزش فیزیک – پایه دوازدهم در فرادرس

کلیک کنید

علامت منفی نشان ‌دهنده مخالفت فنر با جابه‌جایی صورت گرفته در آن، $$x$$ جابه‌جایی فنر از حالت تعادل و $$k$$ ثابت فنر است. همان گونه که از رابطه بالا مشخص است، هر چه جابه‌جایی فنر بیشتر باشد نیروی فنر از نظر مقدار بزرگتر می‌شود و مخالفت بیشتری با نیروی خارجی وارد شده نشان خواهد داد. $$k$$ یا ثابت فنر در قانون هوک بستگی به شکل و جنس فنر دارد. این ثابت نشان دهنده میزان سخت بودن فنر بوده و واحد آن $$\frac{N}{m}$$ یا $$\frac{N}{cm}$$ است.

ترکیب فنرها

واضح است که در ابزاری که با فنر کار می‌کنند، یک فنر به کار نرفته و ترکیب چندین فنر باعث به وجود آمدن یک عملکرد نهایی شده است. به همین دلیل مهم است بدانیم زمانی که دو یا چند فنر در سیستم قرار می‌گیرند ثابت فنر‌ها به صورت مجموع، چگونه محاسبه می‌شود.

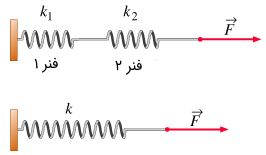
ترکیب سری فنرها

اگر فنرها پشت سر یکدیگر قرار گیرند، یک ترکیب سری از فنرها را داریم. در این حالت ثابت فنر حاصل برابر است با:

$$\large \frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\cdot\cdot\cdot$$

مشخص است که در این حالت فنر حاصل از ترکیب فنرها، ثابتی کوچکتر از ثابت هر یک از فنرها دارد.

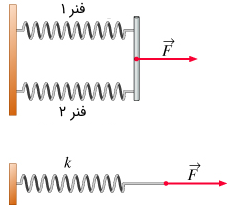
ترکیب موازی فنرها

اگر فنرها روبه‌روی یکدیگر قرار گیرند، یک ترکیب موازی از آنها داریم. در این حالت ثابت فنر حاصل برابر است با:

$$\large k=k_1+k_2+\cdot\cdot\cdot$$

مشخص است که در این حالت فنر حاصل از ترکیب فنرها، ثابتی بزرگتر از ثابت هر یک از فنرها دارد.

انرژی پتانسیل کشسانی

نیروی فنر یک نیروی پایستار است، به این معنی که بزرگی آن به مسیر حرکت بستگی ندارد. با استفاده از قضیه کار و انرژی، انرژی پتانسیل کشسانی فنر به صورت زیر به دست می‌آید:

$$\large U=-\int F dx=\int_{x_{i}}^{x_{f}}kx\ dx=\frac{1}{2}k(x_f^2-x_i^2)$$

نوسان فنر

اگر یک فنر فشرده یا کشیده شود، حرکت نوسانی انجام می‌دهد (از نیروهایی مانند اصطکاک یا مقاومت هوا صرف‌نظر می‌کنیم). نوسان جسمی به جرم $$m$$ که از فنری آویزان شده است را می‌توان با کمک قانون دوم نیوتن بررسی کرد و به صورت زیر نوشت:

$$\large m\ddot{x}=ma=F=-kx$$

فیلم آموزش فیزیک پایه 1 – جامع و کاربردی در فرادرس

کلیک کنید

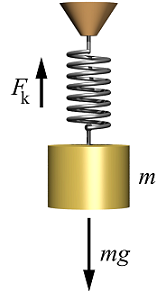
در نتیجه، معادله حرکت جسمی به جرم $$m$$ که از فنری با ثابت $$k$$ آویزان شده، برابر است با:

$$\large\ddot{x}+\frac{k}{m}x=0\quad\quad (1)$$

دقت کنید که از رابطه میان مکان و شتاب در روابط بالا کمک گرفته‌ایم. معمولاٌ در فیزیک نمادگذاری $$\frac{k}{m}=\omega_0^2$$ را در نظر می‌گیریم و به $$\omega_0^2$$ فرکانس طبیعی سیستم می‌گوییم. جواب معادله (۱) به صورت زیر به دست می‌آید:

$$\large x(t)=A\cos(\omega_{0}t)+B\sin(\omega_{0}t) \quad\quad (2)$$

که مقدار $$A$$ و $$B$$ با توجه به شرایط مرزی مسئله قابل محاسبه است. معادله (۲) را در فیزیک معادله نوسانگر هماهنگ ساده می‌نامیم. واضح است که به دلیل وجود نیروهای میرا، این نوسان تا ابد ادامه نمی‌یابد و بعد از مدت زمانی متوقف می‌شود. در حقیقت نوسان فنر، یک نوسان میرا است.

نقاط کمینه پتانسیل و اختلالات کوچک

اگر به یک سیستم فیزیکی با تعادل پایدار، اختلال کوچکی وارد شود، شروع به نوسان حول نقطه تعادل کرده که این نوسان به خوبی توسط قانون هوک توضیح داده می‌شود.

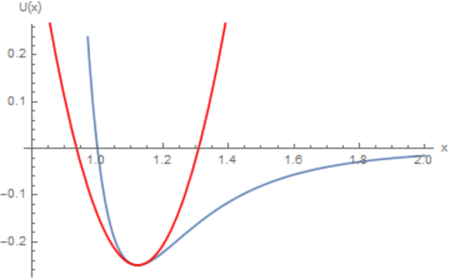
نمودار شکل (۴)، تغییرات انرژی پتانسیل بر حسب مکان جسم را نشان می‌دهد. نقطه کمینه انرژی پتانسیل در این نمودار را «چاه ‌پتانسیل» (Potential Well) می‌نامیم (هر نقطه کمینه پتانسیل چاه نیست، نقاط کمینه‌ای از پتانسیل را چاه می‌نامیم که همانند چاه، حالت مقعر شکل داشته باشند و جسم بدون داشتن انرژی جنبشی کافی، نتواند چاه ‌پتانسیل را ترک کند. چاه پتانسیل را یک نقطه تعادل پایدار می‌گوییم). از نمودار آبی می‌توان دریافت کرد که جسم انرژی جنبشی کافی برای فرار از چاه پتانسیل را ندارد و در اطراف همین نقطه حرکت می‌کند. اگر نقطه $$x_{0}$$ را مکان نقطه تعادل پایدار در شکل (۴) در نظر بگیریم و اختلال کوچکی به سیستم وارد کنیم، سیستم شروع به نوسان حول چاه ‌پتانسیل می‌کند. اگر پتانسیل را حول نقطه $$x_{0}$$ بسط دهیم، داریم:

$$\large U(x) \approx U(x_0) + \left. \frac12 (x-x_0)^2 \frac{d^2 U}{dx^2} \right|_{x=x_0}\quad\quad (3)$$

عبارت دوم سمت راست معادله (۳)، نمایانگر تغییرات انرژی پتانسیل بر حسب مکان است. اگر کمی به این عبارت دقت کنید، شباهت زیادی بین این جمله و انرژی پتانسیل کشسانی فنر خواهید یافت. انرژی پتانسیل کشسانی فنر را برابر با $$\frac{1}{2}kx^2$$ به دست آوردیم، در معادله (۳) نیز جمله دوم بسط تیلور برابر با $$\left. \frac12 (x-x_0)^2 \frac{d^2 U}{dx^2}\right.$$ است. پس در حقیقت می‌توان گفت جسمی که در چاه پتانسیل دچار اختلال کوچکی شود، مانند حالتی که فنری در سیستم وجود دارد، حول نقطه تعادل شروع به نوسان می‌کند و این نوسان از قانون هوک پیروی خواهد کرد.

برای سیستم‌های چند‌ ذره‌ای، جرم سیستم را به صورت جرم کاهیده و به صورت زیر تعریف می‌کنیم:

$$\large \frac{1}{\mu} = \frac{1}{m_1} + \frac{1}{m_2} + \cdots$$

بدین ترتیب، برای این نوسان، فرکانس طبیعی حرکت برابر است با:

$$\large \omega = \sqrt{\frac{1}{\mu} \left. \frac{d^2 U}{dx^2} \right|_{x=x_0}}$$

برای فهم بیشتر مطالب گفته شده، این مطلب را با حل چند مثال به پایان می‌رسانیم.

مثال‌هایی از قانون هوک

مثال ۱: با استفاده از قانون هوک و یک فنر که از قانون هوک پیروی می‌کند، چگونه می‌توان جرم یک جسم را محاسبه کرد؟

حل: جسمی که می‌خواهیم جرم آن را محاسبه کنیم به صورت عمودی از فنری با طول اولیه $$x$$ آویزان می‌کنیم، بعد از آویزان کردن جسم به دلیل نیروی گرانش که به جسم وارد می‌شود طول فنر به اندازه $$\Delta x$$ افزایش می‌یابد. با استفاده از قانون دوم نیوتن داریم:

$$\large mg=-k\ \Delta x\rightarrow m=|\frac{-k\Delta x}{g}|$$

مثال ۲: جسمی به جرم $$m$$ به فنری با ثابت $$k$$ متصل شده که آن را به اندازه $$x$$ از حالت تعادل جابه‌جا کرده و باعث نوسان فنر می‌شود. بیشترین سرعتی که این جسم تجربه می‌کند، چه قدر است (از نیروی مقاومت هوا صرف نظر کنید)؟

حل: با استفاده از اصل پایستگی انرژی، انرژی جنبشی و انرژی کشسانی فنر داریم:

$$\large \frac12 mv^2 = \frac12 kx^2$$

$$\large \rightarrow v=x\sqrt{\frac{k}{m}}$$

مثال ۳: جسمی به جرم $$m$$ به دو فنر که ثابت هر یک از آن‌ها $$k$$ است مانند شکل زیر متصل شده است. اگر این جسم باعث بیشترین جابه‌جایی $$L$$ در سیستم شود، معادله حرکت جسم بر حسب زمان چگونه است؟

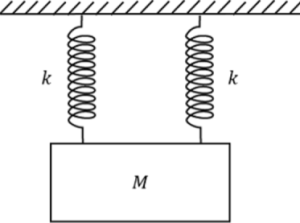
حل: معادله حرکت نوسانی فنر به صورت زیر به دست آمد:

$$\large x(t)=A\cos(\omega_{0}t)+B\sin(\omega_{0}t)$$

از طرفی چون فنرها به صورت موازی با یکدیگر ترکیب شده‌اند، ثابت کل فنر برابر است با:

$$\large k=k_1+k_2\rightarrow2k$$

و معادله حرکت به صورت زیر تغییر می‌کند:

$$\large x(t)=A\cos(\sqrt{\frac{2k}{m}}t)+B\sin(\sqrt{\frac{2k}{m}}t)$$

برای حل این مسأله، مبدأ زمان را لحظه‌ای در نظر می‌گیریم که جسم در پایین‌ترین نقطه قرار دارد و به اندازه $$L$$ جابه‌جا شده است، در این صورت داریم:

$$\large x(0)=L\quad\quad \dot{x}(0)=0$$

اگر معادله حرکت و مشتق معادله حرکت نسبت به زمان (یعنی سرعت) را برای لحظه صفر برای این سیستم بنویسیم، ثابت‌های $$A$$ و $$B$$ به راحتی به دست می‌آیند:

$$\large x(0)=A=L\quad\quad \dot{x}(0)=B\sqrt{\frac{2k}{m}}=0\rightarrow B=0$$

و معادله حرکت این سیستم به صورت زیر محاسبه می‌شود:

$$\large x(t) = L\cos \left(\sqrt{\frac{2k}{m}}t \right)$$

مثال ۴: پتانسیل لنارد-جونز را به صورت زیر در نظر بگیرید:

$$\large U = \epsilon \left[ \left(\frac{r_m}{r} \right)^{12} - 2\left( \frac{r_m}{r} \right)^6 \right]$$

که $$\epsilon$$ عمق چاه پتانسیل را مشخص می‌کند و $$r_{m}$$ عمیق‌ترین نقطه در چاه پتانسیل است. فرکانس طبیعی نوسانات مربوط به حرکت دو جسم با جرم‌های $$m$$ حول نقطه تعادل چاه پتانسیل چه‌قدر است؟

حل: با توجه به اینکه سیستم از دو جسم با جرم های مساوی تشکیل شده است، جرم کاهیده برابر با $$\mu = \frac{m}{2}$$ است. اگر معادله‌ پتانسیل را حول نقطه تعادل یعنی $$r_{m}$$ تا مرتبه دوم بسط دهیم، داریم:

$$\large U(r) \approx -\epsilon + 36 \frac{\epsilon}{r_m^2} (r-r_m)^2$$

با در نظر گرفتن جمله دوم این بسط و رابطه $$\omega_0 = \sqrt{\frac{1}{\mu} \left. \frac{d^2 U}{dx^2} \right.}$$ فرکانس به صورت زیر به دست می‌آید:

$$\large \omega_0 = \sqrt{\frac{2}{m} 72 \frac{\epsilon}{r_m^2}} = \frac{12}{r_m} \sqrt{\frac{\epsilon}{m}}$$