عبارت جبری چیست و چند جمله دارد؟ + مثال و تمرین
در این آموزش از مجموعه مطالب ریاضی مجله فرادرس، با یکی از مفاهیم مهم در جبر و ریاضیات آشنا میشویم که احتمالاً نام آن را بسیار شنیدهاید. این مفهوم، عبارت جبری است که در این آموزش درباره آن بحث میکنیم.


عبارتهای جبری عبارتهایی هستند که با انجام عملیاتی مانند جمع، تفریق، ضرب، تقسیم و غیره بین متغیرها حاصل میشوند. برای مثال، فرض کنید احمد و حسن با چوب کبریت بازی میکنند و میخواهند با استفاده از آنها الگوهای عددی بسازند. احمد ۴ چوب کبریت برداشته و عددی را میسازد. حسن ۳ چوب کبریت دیگر اضافه کرده تا از همان عدد دو تا را تشکیل دهد. آنها متوجه میشوند که میتوانند به اضافه کردن 3 چوب کبریت در هر دور ادامه دهند تا یک عدد متشابه اضافه بسازند. از این بازی، آنها به این نتیجه میرسند که به طور کلی به چوب کبریت نیاز دارند تا الگویی با عدد را بسازند. در اینجا یک عبارت جبری نامیده میشود. همانطور که میبینیم، میتواند تغییر کند. در ادامه، با مفهوم ریاضی عبارت جبری آشنا میشویم.
عبارت جبری چیست ؟
یک عبارت جبری (Algebraic Expression) یا یک عبارت متغیر ترکیبی از جملهها (Terms) با عملیاتی مانند جمع، تفریق، ضرب، تقسیم و غیره است. برای مثال، عبارت را در نظر بگیرید. عبارت نمونهای از عبارت جبری است. یک عبارت جبری اجزای مختلفی دارد. در ادامه، این اجزا را معرفی خواهیم کرد.
اجزای یک عبارت جبری
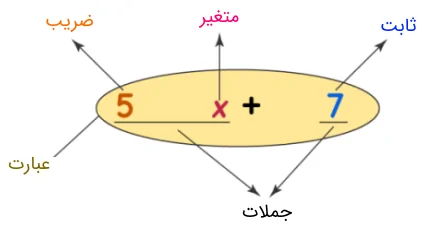
یک عبارت جبری سه بخش دارد: متغیر، ثابت و ضریب. شکل زیر بهخوبی این اجزا را نشان میدهد.
در ریاضیات، نمادی که مقدار ثابتی ندارد، متغیر (Variable) نامیده میشود. متغیر هر مقداری میتواند داشته باشد. در مثال بالا که راجع به چوب کبریت بیان کردیم، یک متغیر است و در این مثال میتواند مقادیر و و و... را بگیرد. برخی از نمادهای رایجی که بهعنوان متغیر در ریاضی استفاده میشوند، و و و و و و و امثال اینهاست.
از طرف دیگر، به نمادی که مقدار عددی ثابتی دارد، ثابت (Constant) میگویند. همه اعداد ثابت هستند. چند مثال از ثابتها عبارتند از و و و و... . یک جمله یک متغیر به تنهایی یا یک ثابت به تنهایی یا ترکیبی از ضرب و تقسیم متغیرها و ثابتها است. برای مثال، و و و و امثال اینها جمله هستند. جملهها با علامت جمع یا تفریق از هم جدا میشوند. اعدادی که در متغیرها ضرب میشوند، ضریب (Coefficient) نام دارند.
تفاوت عبارت جبری و معادله چیست؟
معادله یک گزاره ریاضی است که تساوی دو عبارت را بیان میکند و این تساوی با علامت “=” نمایش داده میشود.
برای مثال، جمله زیر یک عبارت است:
و جملهای که در پایین آمده است، یک معادله را نشان میدهد:
جملات متشابه و غیرمتشابه
یکی از مفاهیم مهم در عبارتهای جبری که باید با آن آشنا باشیم، جملات متشابه و غیرمتشابه هستند. جملات متشابه جملاتی هستند که عوامل (متغیرهای) جبری یکسانی دارند. در طرف مقابل، جملات غیرمتشابه جملاتی هستند که عوامل جبری متفاوتی دارند. برای مثال، در عبارت جبری ، جملات و جملات متشابه هستند، زیرا هر دو دارای عامل مشترک هستند. اما دو جمله و غیرمتشابه هستند، زیرا عوامل مشترکی ندارند و عوامل آنها بهترتیب و است. از این مفاهیم در فاکتورگیری و تجزیه عبارتهای جبری استفاده فراوانی میشود.
انواع عبارتهای جبری
عبارتهای جبری را میتوان بر اساس موارد مختلفی دستهبندی کرد که در ادامه به مهمترین آنها اشاره میکنیم.
انواع عبارتهای جبری بر اساس تعداد جملات
بر اساس تعداد جملات، سه نوع عبارت جبری وجود دارد:
- عبارت تکجملهای: عبارت تکجملهای یک عبارت جبری است که فقط یک جمله دارد. برای مثال، و و و عبارت تکجملهای هستند، زیرا تنها یک جمله دارند.
- عبارت دوجملهای: عبارت دوجملهای نوعی عبارت جبری است که دو جمله دارد. برای مثال، و عبارت دوجملهای هستند.
- عبارت چندجملهای: در حالت کلی، یک عبارت با بیش از دو جمله را عبارت چندجملهای مینامیم. برای مثال، و چندجملهای هستند.
نکته: برای سادگی، در ادامه، گاهی کلمه «جبری» را حذف میکنیم و هر جا کلمه عبارت را بهکار ببریم، منظورمان عبارت جبری است.
انواع عبارتهای جبری بر اساس نوع جمله
به غیر از انواع عبارات تکجملهای، دوجملهای و چندجملهای، یک عبارت جبری را میتوان به دو نوع دیگر نیز طبقهبندی کرد که عبارتاند از:
- عبارت عددی: یک عبارت عددی از اعداد و عملیات مختلف ریاضی تشکیل شده است، اما شامل هیچ متغیری نیست. برخی از مثالهای عبارات عددی و و غیره هستند.
- عبارت متغیر: عبارت متغیر عبارتی است که شامل متغیرها به همراه اعداد و عملیات ریاضی مختلف برای تعریف یک عبارت است. چند نمونه از عبارت متغیر عبارتاند از و .
نکته: با اینکه عبارت عددی یک عبارت جبری است، ام معمولاً منظورمان از عبارت جبری، یک عبارت جبری دارای متغیر است.
انواع عبارتهای جبری براساس تعداد متغیرها
بر اساس تعداد متغیرها، عبارتهای جبری را میتوان به دستههای زیر تقسیم کرد:
- عبارت جبری تکمتغیره: این عبارتهای جبری تنها یک متغیر دارند. برای مثال، و و و... .
- عبارت جبری دومتغیره: این عبارات جبری، همانطور که از نامشان پیداست، دو متغیر دارند. برای مثال، و و و و و و... .
- عبارت جبری سهمتغیره: عبارت جبری سهمتغیره دارای سه متغیر است. برای مثال، و و... .
- عبارت جبری با متغیرهای بیشتر: نوعی از عبارتهای جبری نیز بیش از سه متغیر دارند.

عملیات ریاضی روی عبارتهای جبری
روی عبارتهای جبری میتوان عملیات حسابی مختلف را انجام داد. در ادامه، این عملیات را معرفی میکنیم.
جمع عبارتهای جبری
در جمع عبارتهای جبری، فقط جملات متشابه آنها با هم جمع میشود. در این حالت، ضرایب این جملات با هم جمع جبری میشود. اما جملات غیرمتشابه را به همان شکلی که هستند و با همان علامتی که دارند، بدون تغییر میگذاریم.
برای مثال، جمع دو عبارت و بهصورت زیر خواد بود:
در عبارت اخیر، جملات متشابه را با هم جمع جبری کردهایم.
تفریق عبارتهای جبری
برای تفریق عبارتهای جبری کافی است عبارت اول را با قرینه عبارت دوم جمع کنیم. در این مورد نیز، جملات متشابه از هم تفریق میشوند. برای مثال، فرض کنید میخواهیم را از کم کنیم. بنابراین، مینویسیم:
که جواب آن بهصورت زیر خواهد بود:
ضرب عبارتهای جبری
برای ضرب عبارتهای جبری، باید جملات را تکتکدر هم ضرب کنیم. برای مثال، فرض کنید دو عبارت جبری و را داریم. میخواهیم این دو عبارت را در هم ضرب کنیم. اینگونه عمل میکنیم:
یا ضرب دو عبارت و برابر است با

تقسیم عبارتهای جبری
تقسیم عبارتهای جبری را نیز میتوان به روشهای مختلفی مانند روش مستقیم یا استفاده از اتحادهای جبری انجام داد. برای مثال، تقسیم زیر با کمک اتحادها بهصورت زیر انجام میشود:
ساده سازی عبارتهای جبری
سادهسازی عبارتهای جبری یعنی اینکه یک عبارت جبری را بهگونهای ساده کنیم که جملات متشابه در آن وجود نداشته باشند. برای سادهسازی عبارات جبری، جملات متشابه را با هم جمع یا تفریق میکنیم و اگر ضرب عبارتها وجود داشته باشد، آن را انجام میدهیم. در نهایت، پس از سادهسازی، باید یک عبارت داشته باشیم که از مجموع جملات غیرمتشابه تشکیل شده است.
برای مثال، فرض کنید میخواهیم عبارت زیر را ساده کنیم:
با انجام ضرب، این عبارت ساده میشود و خواهیم داشت:
یا عبارت زیر را در نظر بگیرید:
ابتدا ضرب را انجام میدهیم، سپس جملات متشابه را با هم جمع میکنیم:
تجزیه عبارتهای جبری
وقتی میگوییم یک عبارت جبری را تجزیه کنیم، منظور این است که آن عبارت را که بهصورت مجموع چند جمله بیان شده، بهشکل حاصلضرب چندجملهایها بنویسیم. برای مثال، عبارت جبری ساده را در نظر بگیرید. با فاکتور گرفتن از ، این عبارت ساده را میتوان بهصورت زیر نوشت:
میبینیم که یک عبارت جبری که بهصورت مجموع جملات جبری بود، بهشکل ضرب دو چندجملهای نوشته شده است.
اما علاوه بر موارد سادهای مانند فاکتورگیری، اتحادها نقش بسیار مهمی در تجزیه عبارتهای جبری دارند. برای مثال، عبارت جبری با کمک اتحادها (در ادامه مهمترینشان را معرفی میکنیم) بهصورت زیر تجزیه میشود:
در تجزیه عبارت های جبری یا همان چندجملهایها معمولاً از اتحادها و همچنین، فاکتورگیری کمک میگیریم.
گاهی شکل ظاهری چندجملهای دقیقاً مانند اتحادهای معروف است. در این صورت به راحتی میتوانیم از اتحادها استفاده کرده و تجزیه عبارتهای جبری را به خوبی انجام دهیم. البته گاهی باید از تکنیکهای ریاضی استفاده کنیم، تکنیکهایی مانند کم و زیاد کردن جملات جدید، شکستن جملات موجود و... . برای تجزیه آسان عبارت های جبری میتوانیم از فاکتورگیری نیز استفاده کنیم. در مثالهایی که در ادامه بیان میکنیم، به این موارد اشاره خواهیم کرد.
مهمترین اتحادهایی که از آنها در تجزیه عبارت های جبری استفاده میشود، عبارتاند از:
- اتحاد مربع دوجملهای:
- اتحاد مربع سهجملهای:
- اتحاد بسط دوجملهای نیوتن:
- اتحاد لاگرانژ:
- اتحاد اویلر:
برای تجزیه عبارتهای جبری، ابتدا عبارت را به دقت بررسی کنید و به دنبال اشتراک در جملهها باشید تا در صورت امکان از فاکتورگیری استفاده کنید. مثلاً در عبارت اگر کمی دقت کنیم، میبینیم که در همه جملات متشابه است و میتوان عبارت را به صورت نوشت.
نکته دیگر که بسیار به تجزیه عبارت های جبری کمک میکند، استفاده از اتحادها است. به همین دلیل، بهتر است همه اتحادهای مهم را به خاطر بسپارید و عبارت جبری را از جنبه اتحادها بررسی کنید.

حل معادلات جبری
هدف از حل یک معادله جبری که از عبارتهای جبری تشکیل شده است، یافتن متغیر مجهول است. هنگامی که دو عبارت برابر میشوند، یک معادله را تشکیل میدهند، و بنابراین، حل آن برای جملات مجهول آسانتر میشود.
برای حل یک معادله، متغیرها را در یک طرف و ثابتها را در طرف دیگر قرار دهید. میتوانید متغیرها را با به کار بردن عملیات حسابی مانند جمع، تفریق، ضرب، تقسیم، جذر، ریشه مکعب و غیره جدا کنید.
یک عبارت جبری را میتوان همواره به طرف دیگر تساوی انتقال داد، به شرطی که علامت آن را قرینه کنیم. این بدان معناست که میتوانیم معادله را با تعویض سمت چپ تساوی با سمت راست تساوی بازنویسی کنیم.
برای مثال، میخواهیم مقدار را از معادله زیر بیابیم:
معادلهای که داریم، است. برای حل معادله، متغیرها و ثابتها را جدا میکنیم. میتوانید متغیر را در سمت چپ تساوی و ثابتها را در سمت راست تساوی قرار دهیم:
سمت راست را ساده میکنیم:
دو طرف را بر ضریب متغیر تقسیم میکنیم:
بنابراین مقدار برابر است.
مقدار عددی عبارت جبری
مقدار عددی عبارت جبری یعنی اینکه بهجای متغیرها عدد قرار دهیم و مقدار عبارت را حساب کنیم. برای مثال، فرض کنید عبارت را داریم. بهازای ، مقدار عددی این عبارت برابر با است.
مثالهای عبارت جبری
در این بخش، مثالهای متنوعی را از عبارتهای جبری بررسی میکنیم.
مثال اول عبارت جبری
آیا یک عبارت جبری است؟
حل: بله، یک عبارت جبری است. فرض کنید متغیر فرضی را داشتهایم. در این صورت، را میتوان بهصورت زیر بیان کرد:
در مثالی دیگر میتوان به شکل زیر بیان کرد.
مثال دوم عبارت جبری
آیا عبارتهای جبری چندجملهای هستند؟
جواب: خیر، همه عبارات جبری چندجملهای نیستند. اما همه چندجملهایها عبارتهای جبری هستند. تفاوت این است که چندجملهایها فقط شامل متغیرها و ضرایب با عملیات ریاضی (جمع، تفریق و ضرب) میشوند، اما عبارات جبری شامل توانهای گنگ نیز میشوند. همچنین، چندجملهایها توابع پیوستهای هستند (مثلاً )، اما عبارت جبری ممکن است گاهی اوقات پیوسته نباشد (به عنوان مثال در پیوسته نیست).

مثال سوم عبارت جبری
عبارت جبری زیر را ساده کنید:
حل: جملات را تکتک در هم ضرب میکنیم و خواهیم داشت:
مثال چهارم عبارت جبری
مجموع سه عدد زوج متوالی است. این اعداد را بهدست آورید.
حل: سه عدد را بهشکل عبارتهای جبری در نظر میگیریم: عدد نخست: ، عدد دوم و عدد سوم: .
جمع این سه عدد برابر است با
بنابراین، این اعداد عبارتاند از و و .
مثال پنجم عبارت جبری
صحیح و غلط بودن موارد زیر را مشخص کنید:
- ضریب عددی عدد است.
- دو تکجملهای و متشابه هستند.
- دو جمله که پیکربندی متغیرهای آنها با هم یکسان باشد، متشابه هستند.
- ضریب عددی جمله عدد است.
جواب: ۱) غلط، ۲) غلط، ۳) صحیح، ۴) صحیح.
مثال ششم عبارت جبری
عبارتهای و و را با هم جمع کنید.
حل: جواب بهصورت زیر است:
مثال هفتم عبارت جبری
عبارت را از کم کنید.
حل: جواب بهصورت زیر است:
مثال هشتم عبارت جبری
عبارت جبری زیر را ساده کنید:
حل: این عبارت، با توجه به آنچه گفتیم، بهصورت زیر ساده میشود:

مثال نهم عبارت جبری
سه عبارت و و را در هم ضرب کنید.
حل: با ضرب تکتک جملات در هم، خواهیم داشت:
مثال دهم عبارت جبری
مقدار عددی عبارت زیر را بهازای و محاسبه کنید.
حل: مقادیر و را در عبارت قرار میدهیم و خواهیم داشت:
مثال یازدهم عبارت جبری
عبارت جبری زیر را تجزیه کنید:
حل: با فاکتورگیری از ، این عبارت بهصورت زیر تجزیه میشود:
مثال دوازدهم عبارت جبری
عبارت جبری را ساده کنید.
حل: ابتدا ضربها را انجام میدهیم، سپس جملات متشابه را با هم جمع میکنیم:
جمعبندی
در این آموزش از مجله فرادرس، با عبارت جبری و اجزای آن آشنا شدیم. همچنین، انواع عبارتهای جبری را بر اساس عوامل مختلف معرفی کردیم. علاوه بر این موارد، مطالبی را درباره سادهسازی و تجزیه عبارتهای جبری همراه با معرفی اتحادهای مهم ارائه کردیم.
آزمون عبارت جبری
۱. کدام ویژگی مشخصه اصلی عبارت جبری در مقایسه با معادله است؟
عبارت جبری همیشه شامل عبارت مربع یا مکعب است.
عبارت جبری معمولا بیش از دو متغیر دارد.
عبارت جبری فقط شامل متغیر و عدد است و نشانه مساوی (=) ندارد.
عبارت جبری باید جمع و تفریق همزمان داشته باشد.
عبارت جبری ترکیبی از متغیرها و اعداد است بدون اینکه نشانه مساوی (=) داشته باشد؛ یعنی بر خلاف معادله که رابطه تساوی را نمایش میدهد، عبارت جبری فقط بیانگر یک ترکیب عددی و متغیر است. اینکه عبارت جبری همیشه مربع یا مکعب باشد یا بیش از دو متغیر داشته باشد درست نیست؛ زیرا ممکن است فقط یک متغیر یا حتی فقط عمل ساده جمع یا تفریق داشته باشد. لازم نیست همیشه جمع و تفریق همزمان وجود داشته باشد، بلکه امکان دارد فقط یک عمل ریاضی در عبارت باشد.
۲. برای تشخیص اجزای یک عبارت جبری کدام دسته از عناصر باید بررسی شوند؟
فرمولهای اتحاد
اعداد زوج و فرد
علامتهای جمع و تفریق
متغیر، ثابت و ضریب
برای شناسایی اجزای یک عبارت جبری لازم است سه عنصر «متغیر، ثابت و ضریب» را مورد توجه قرار دهیم زیرا اینها اجزای اصلی عبارت جبری به شمار میروند. «اعداد زوج و فرد» فقط دسته خاصی از اعداد هستند و «فرمولهای اتحاد» به کار تجزیه و سادهسازی میآیند، نه شناسایی اجزا. «علامتهای جمع و تفریق» نیز فقط عملیات ریاضی را نشان میدهند و خود به عنوان اجزای عبارت جبری محسوب نمیشوند.
۳. در عبارت جبری 3x+2، کدام مورد ضریب و کدام مورد ثابت است؟
عدد ۳ ثابت است و عدد ۲ متغیر است.
عدد ۳ و ۲ هر دو ضریب هستند.
عدد ۲ ضریب است و عدد ۳ ثابت این عبارت است.
عدد ۳ ضریب متغیر x است و عدد ۲ ثابت است.
در عبارت جبری 3x+2، عدد ۳، ضریب کنار متغیر x محسوب میشود و عدد ۲ نیز مقدار ثابتی است که مستقل از متغیر قرار دارد. براساس تعریف ارائهشده، ضریب همان عددی است که کنار متغیر ظاهر میشود و ثابت عددی است که بدون متغیر در عبارت قرار دارد.
۴. در فرآیند سادهسازی یک عبارت جبری که شامل جملههای ۲xy و -۴xy باشد، این دو جمله چه رابطهای پیدا میکنند؟
به دلیل تفاوت ضرایب، هیچ تاثیری بر هم ندارند و جدا باقی میمانند.
این دو جمله با هم جمع میشوند و حاصل یک جمله جدید با همان متغیر میشود.
تنها ضرایب تغییر میکنند اما متغیر از بین میرود.
سادهسازی تنها شامل حذف ضرایب مثبت است و این دو جمله حذف نمیشوند.
در سادهسازی، جملاتی که متغیرهای یکسانی دارند متشابه شمرده میشوند. جملههای «۲xy» و «-۴xy» هر دو متشابهاند، بنابراین ضرایب آنها با هم جمع شده و یک جمله جدید با متغیر xy ایجاد میشود.
۵. کدام نوع دستهبندی برای عبارت براساس تعداد جملهها صحیح است؟
دوجملهای
تکجملهای
چندجملهای (سه جملهای)
عبارت عددی بدون متغیر
عبارت از سه جمله یعنی و و تشکیل شده است.
۶. برای جمع و تفریق جملات متشابه در عبارات جبری چه اصلی اهمیت دارد؟
هر جمله جبری را میتوان با هر جمله دیگری جمع یا تفریق کرد حتی اگر متغیرها متفاوت باشند.
فقط جملات ثابت قابل جمع یا تفریق با یکدیگر هستند.
تنها جملاتی را میتوان جمع یا تفریق کرد که متغیرهای یکسان داشته باشند.
جمع و تفریق جملات فقط اگر ضرایب برابر باشند مجاز است.
در جمع و تفریق جملات متشابه در عبارت جبری، باید جملاتی را انتخاب کرد که دقیقا متغیرهای یکسان داشته باشند؛ یعنی ساختار متغیرها و توانهای آنها یکی باشد. تنها در این حالت ترکیب یا کمکردن ضرایب آن جملات ممکن است. جملاتی که متغیرهای متفاوت دارند، مثل یک جمله با x و جمله دیگر با xy، قابل جمع یا تفریق با یکدیگر نیستند. جملههایی که فقط ضرایب برابر دارند یا صرفا ثابت هستند، شرط کافی برای جمع یا تفریق نیستند مگر اینکه متغیر دادن نداشته باشند. بنابراین رعایت یکسان بودن متغیرها اصل اساسی در جمع و تفریق جملات متشابه است.
۷. در روند سادهسازی عبارت جبری، دلیل این که فقط جملات متشابه را باید باهم جمع یا تفریق کرد چیست؟
زیرا فقط جملات متشابه متغیرهای یکسان دارند و قابل جمع شدن هستند.
برای این که ترتیب نوشتن عبارات اهمیت دارد و باید مشابه بماند.
چون جمع هر جملهای باعث کوتاهتر شدن عبارت خواهد شد.
چون جملات غیرمتشابه عددی هستند و نیازی به ترکیب ندارند.
فقط جملات متشابه، یعنی جملههایی که متغیر و توان یکسان دارند، قابلیت جمع یا تفریق دارند چون از یک نوع هستند و مقدارهایشان را میتوان با هم یکی کرد. جمع کردن جملات غیرمتشابه ممکن نیست چون متغیرها یا توانها متفاوت است و باید جداگانه باقی بمانند. عبارت «جمع هر جمله باعث کوتاهتر شدن عبارت» درست نیست چون فقط در مورد جملات متشابه این موضوع صدق میکند. «ترتیب نوشتن عبارات» تاثیری ندارد و «جملات غیرمتشابه عددی هستند» نادرست است چون بسیاری از آنها متغیر دارند.
۸. اگر بهجای متغیر x در عبارت x+۴ عدد ۲ قرار دهیم، نتیجه محاسبه عبارت چیست؟
عدد ۶ بهدست میآید.
عدد ۸ حاصل میشود.
عدد ۴ بهدست میآید.
عدد ۲ حاصل میشود.
در عبارت x+۴ اگر x را با ۲ جایگزین کنیم، محاسبه به صورت ۲+۴ خواهد بود که نتیجه آن برابر با عدد ۶ است.
۹. عبارت تکجملهای، دوجملهای و چندجملهای چگونه از نظر تعداد جملهها ساختاربندی میشوند؟
ساختار عبارت تکجملهای و دوجملهای تفاوتی با چندجملهای ندارد و همگی دارای یک جمله هستند.
عبارت تکجملهای تنها یک جمله دارد، دوجملهای شامل دو جمله و چندجملهای بیش از دو جمله دارد.
عبارت تکجملهای دارای دو جمله، دوجملهای سه جمله و چندجملهای هر تعداد جمله است.
عبارت تکجملهای فقط اعداد را شامل میشود و چندجملهای متغیر دارد.
عبارت تکجملهای از یک جمله ساخته میشود، دوجملهای شامل دقیقا دو جمله و چندجملهای دارای سه جمله یا بیشتر است.
۱۰. در آغاز حل یک معادله جبری، کدام کار باید پیش از انجام هر عملیات دیگر انجام شود و اهمیت آن چیست؟
جمع کردن ضرایب جملات متشابه برای سادهسازی طرفین
جایگذاری اعداد دلخواه به جای متغیر جهت محاسبه مقدار
انتقال همه متغیرها به یک طرف معادله برای جداکردن مجهول
به کار بردن اتحادهای جبری برای فاکتورگیری جملات
در فرایند حل معادله جبری ابتدا باید تمام متغیرها را به یک طرف معادله انتقال داد و ثابتها را به طرف دیگر برد. این کار باعث میشود مقدار نامعلوم یا همان مجهول جدا شود و بتوان مراحل بعدی حل را ادامه داد. جمع کردن ضرایب جملات متشابه، جایگذاری اعداد به جای متغیر و استفاده از اتحادهای جبری در مراحل دیگر انجام میشوند و نقش مرحله آغازین را ندارند، زیرا تا زمانی که متغیرها و ثابتها جدا نشدهاند، معادله به صورت قابل حل برای تعیین مجهول درنیامده است.
۱۱. در هنگام تجزیه عبارات جبری، کدام ویژگی استفاده از اتحاد مربع دوجملهای باعث سهولت کار میشود؟
امکان حذف متغیرهای پیچیده از عبارت
کمک به نوشتن عبارت به صورت حاصلضرب دو جمله مشابه
تبدیل عبارت به صورت جمع جملات متشابه
امکان جایگذاری سریع مقدار متغیرها
استفاده از اتحاد مربع دوجملهای باعث میشود عبارت جبری را به شکل ضرب دو جمله مشابه تبدیل کنیم، که این موضوع فرآیند تجزیه یا فاکتورگیری را سادهتر و ساختار آن را روشنتر میکند. گزینه «نوشتن عبارت به صورت حاصلضرب دو جمله مشابه» درست است، زیرا مربع دوجملهای دقیقا با همین هدف به کار میرود. سایر گزینهها مانند «حذف متغیرهای پیچیده»، «تبدیل به جمع جملات متشابه» یا «جایگذاری سریع مقدار متغیرها» ارتباط مستقیمی با مزیت این اتحاد در فرآیند فاکتورگیری ندارند.













سلام بنظرم در قسمت مثال تفریق عبارت های جبری
۱۰+(۳-) پاسخ برابر۷می شود
پاسخ۱۳ اشتباه است
با سلام و وقت بخیر؛
فرمول اصلاح شد. ممنون از دقت نظر شما
از همراهیتان با مجله فرادرس سپاسگزاریم
خوب بود عبارت ریاضی رو هم تعریف می کردید و فرقش با عبارت جبری
با سلام و خسته نباشيد ، ممنون ميشم جواب اين عبارت رو دوباره بررسي كنيد و توضيح بديد در مورد جواب نهايي
(3x+6y) xy_2x
سلام میشه بگید عبارت جبری 4x_6 چند جمله دارد؟
ممنون
سلام مهدی عزیز.
عبارت مذکور بازبینی و اصلاح شد.
سپاس از همراهی و بازخوردتان.