انرژی درونی – از صفر تا صد

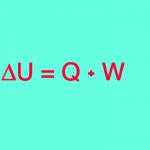
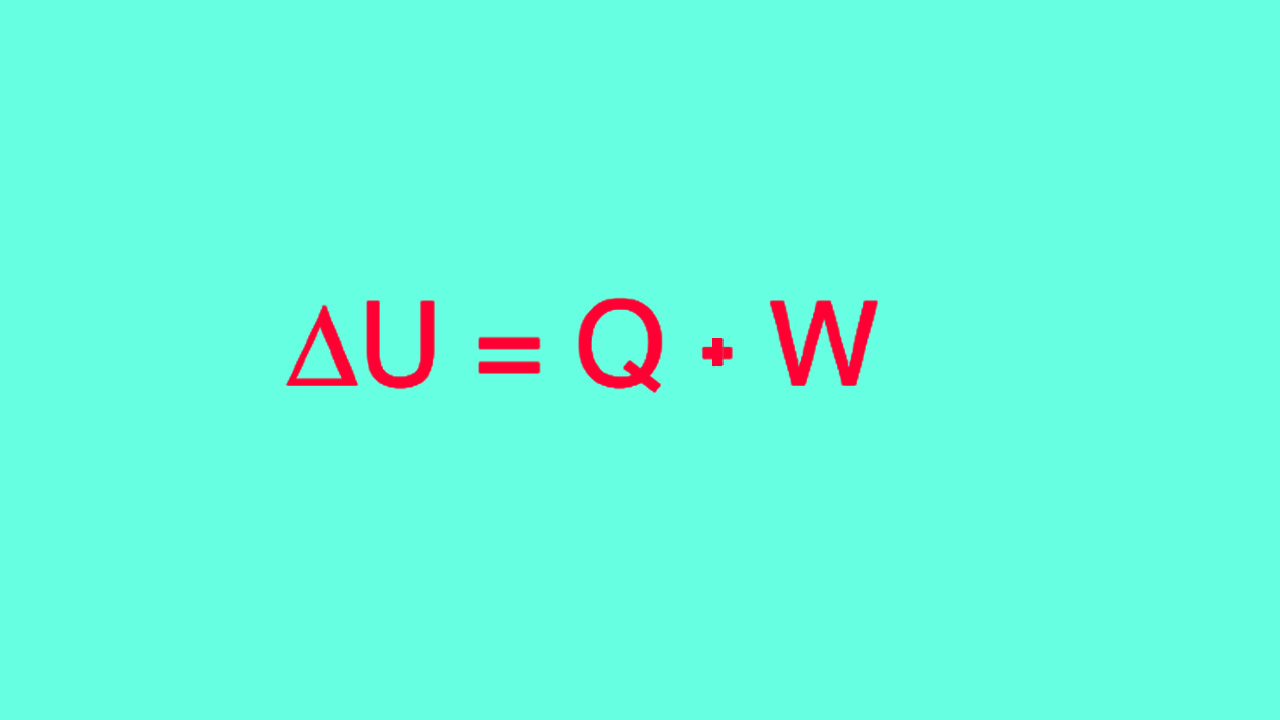
مقدمه

تمامی اشیا در فضا شامل انرژی‌ها ماکروسکوپی و میکروسکوپی هستند. با وجود این‌که این انرژی‌ها، مفاهیم بسیار نزدیکی دارند، اما تفاوت اصلی آن‌ها این است که انرژی میکروسکوپی قابل مشاهده نیست. به طور مثال، یک لیوان آب بر روی میز، هیچ انرژی ماکروسکوپی ندارد اما در مقیاس میکروسکوپی، این لیوان آب در حقیقت، جرمی شامل مولکول‌هایی است که با سرعت بیش از صدها متر بر ثانیه در حال حرکت هستند.

واحد انرژی در SI، ژول $$(J)$$ است. در برخی موارد از از انرژی درونی ویژه استفاده می‌کنند که واحد‌های آن به ترتیب برای جرم سیستم و مقدار ماده (انرژی درونی مولی) به صورت $$J / kg$$ و $$J / mol$$ تعریف می‌شود.

توابع کاردینال

انرژی درونی $$U ( S , V , { N j } )$$، ترمودینامیک یک سیستم را با زبان انرژی بیان می‌کند. به عنوان یک تابع حالت، شناسه‌های آن به صورت «متغیرهای مقداری»‌ (Extensive Variables) از حالت هستند. در کنار انرژی درونی، دیگر تابع حالت کاردینال (اصلی) در یک سیستم ترمودینامیکی، آنتروپی $$S ( U , V , { N j } )$$ است. هر تابع کاردینال، «تابعی یکنوا» (Monotonic Function) از متغیرهای طبیعی یا کانونیک (متعارفی) خود است که هرکدام، معادلاتی اساسی را بدست می‌دهند. به طور مثال، $$U = U ( S , V , { N j } )$$، خود شامل تمامی اطلاعات ترمودینامیکی یک سیستم است.

فیلم آموزش گرمای‌ نهان و محاسبه آن در فرادرس

کلیک کنید

تعریف انرژی درونی

انرژی درونی یک سیستم به کمک جمع زدن انتقال انرژی‌های ماکروسکوپی که سبب تغییر حالت سیستم از حالت مرجع به حالت جدید می‌شوند، قابل محاسبه است:

$$\begin {equation} \Delta U = \sum _ { i } E _ { i } \end{equation}$$

انرژی داخلی (درونی) را می‌توان به صورت مجموع انرژی‌های جنبشی و پتانسیل میکروسکوپی به صورت زیر نوشت:

$$U = U _ {\mathrm{micro\,pot}} + U _ {\mathrm{micro\,kin}}$$

تغییرات انرژی درونی