انتگرال در متلب – راهنمای کامل

در این آموزش، با روش به دست آوردن انتگرال در متلب برای دو دسته کلی انتگرال‌های معین و نامعین آشنا می‌شویم. همچنین، روش حل انتگرال‌های عددی، خطی و دوگانه را نیز بیان می‌کنیم.

انتگرال در متلب

در حالت کلی، انتگرال‌گیری را می‌توان به دو دسته تقسیم کرد. در نوع اول، مشتق یک تابع داده می‌شود و می‌خواهیم خود تابع را پیدا کنیم. بنابراین، ما اساساً روندی عکس مشتق‌گیری انجام می‌دهیم. این فرایند معکوس به عنوان پادمشتق یا یافتن تابع اولیه یا یافتن انتگرال نامعین شناخته می‌شود. نوع دوم شامل جمع کردن تعداد بسیار زیادی از مقادیر بسیار ناچیز و سپس گرفتن حد برای میل این مقادیر به صفر است، در حالی که تعداد جملات به بینهایت میل می‌کند. این فرایند منجر به تعریف انتگرال معین می‌شود. در ادامه، به معرفی روش‌های حل انتگرال در متلب می‌پردازیم.

انتگرال نامعین در متلب

طبق تعریف، اگر مشتق تابع $$f(x)$$ برابر با $$f'(x)$$ باشد، می‌گوییم یک انتگرال نامعین $$f' ( x )$$ برابر با $$f ( x )$$‌ است. به عنوان مثال، از آنجا که مشتق (نسبت به $$x$$) تابع $$x ^ 2$$ برابر با $$2 x$$ است، می‌توان گفت یک انتگرال نامعین تابع $$2 x$$ برابر با $$x ^ 2$$ است.

برای محاسبه انتگرال در متلب از دستور "int" استفاده می‌شود. برای محاسبه انتگرال نامعین تابع $$f$$، دستور زیر را می‌نویسیم:

1int(f);

برای مثال، فرض کنید می‌خواهیم انتگرال تابع $$2 x$$ را به دست آوریم. بدین منظور، برنامه زیر را می‌نویسیم (دستور "syms" در متلب، برای تعریف متغیر‌ها به صورت نمادین به کار می‌رود):

1syms x 
2int(2*x)

که نتیجه حاصل از اجرای آن به صورت زیر خواهد بود:

ans =
   x^2

مثال اول انتگرال نامعین در متلب

در این مثال، می‌خواهیم برای نمونه انتگرال برخی از عبارات متداول را بیابیم. برای این کار، یک فایل اسکریپت ایجاد می‌کنیم و کد زیر را در آن می‌نویسیم:

1syms x n
2
3int(sym(x^n))
4f = 'sin(n*t)'
5int(sym(f))
6syms a t
7int(a*cos(pi*t))
8int(a^x)

اگر این برنامه را اجرا کنیم، نتیجه آن به صورت زیر خواهد بود:

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

مثال دوم انتگرال نامعین در متلب

برنامه زیر را در متلب بنویسد:

1syms x n
2int(cos(x))
3int(exp(x))
4int(log(x))
5int(x^-1)
6int(x^5*cos(5*x))
7pretty(int(x^5*cos(5*x)))
8
9int(x^-5)
10int(sec(x)^2)
11pretty(int(1 - 10*x + 9 * x^2))
12
13int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
14pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

با اجرای این برنامه، خروجی به صورت زیر خواهد بود (استفاده از دستور "pretty" نتایج را مرتب‌تر نشان می‌دهد):

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

انتگرال معین در متلب

طبق تعریف، انتگرال معین اساساً حد یک مجموع است. ما از انتگرال‌های معین استفاده می‌کنیم تا مساحت‌هایی مانند مساحت بین یک منحنی و محور $$x$$ و مساحت بین دو منحنی را پیدا کنیم. انتگرال‌های معین در موارد دیگر نیز مورد استفاده قرار می‌گیرند که در آن‌ها مقدار مورد نیاز را می‌توان به عنوان حد یک مجموع بیان کرد. انتگرال‌های معین برای یافتن مساحت، حجم، مرکز جرم، لختی دورانی، کاری که توسط یک نیرو انجام می‌شود و در بسیاری از کاربردهای دیگر استفاده می‌شوند.

فیلم مجموعه آموزش متلب MATLAB – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

مشابه انتگرال نامعین، برای محاسبه انتگرال معین نیز از تابع "int" در متلب استفاده می‌شود. برای محاسبه انتگرال $$\int _a ^ b f ( x ) d x$$ دستور زیر را می‌نویسیم:

int(x, a, b)

برای مثال، برای محاسبه انتگرال $$\int _4 ^ 9 x d x$$، دستور زیر را خواهیم داشت:

1int(x, 4, 9)

که جواب آن برابر است با:

ans =
   65/2

مثال اول انتگرال معین در متلب

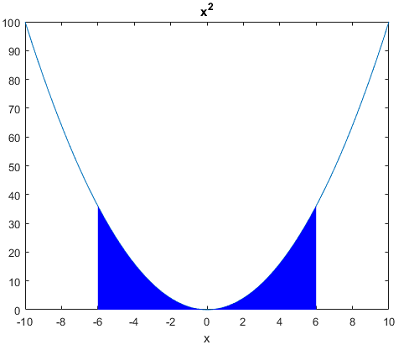
می‌خواهیم مساحت زیر منحنی نمودار $$y = x ^ 3 - 2 x + 5$$ را از $$x = 1$$ تا $$x = 2$$ یا انتگرال $$\int _ 1 ^ 2 (x ^ 3 - 2 x + 5 ) d x$$ را محاسبه کنیم. بدین منظور، برنامه زیر را در متلب می‌نویسیم:

1f = x^3 - 2*x +5;
2a = int(f, 1, 2)
3disp('Area: '), disp(double(a));

که جواب آن به صورت زیر خواهد بود:

a =
23/4
Area: 
   5.7500

مثال دوم انتگرال معین در متلب

می‌خواهیم سطح زیر نمودار تابع $$f ( x ) = x ^ 2 \cos ( x )$$ را در بازه $$- 4 \le x \le 9$$ به دست آوریم. برای محاسبه این انتگرال، کد زیر را در متلب می‌نویسیم:

1f = x^2*cos(x);
2ezplot(f, [-4,9]);
3a = int(f, -4, 9);
4disp('Area: '), disp(double(a));

که حاصل آن، شکل و مقدار عددی زیر است:

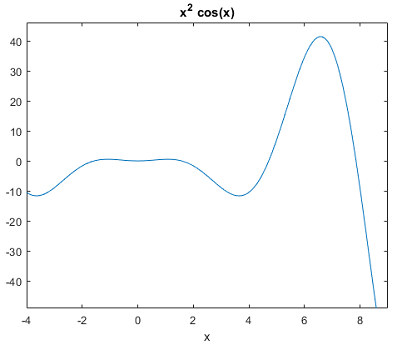
a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

مثال سوم انتگرال معین در متلب

می‌خواهیم انتگرال زیر را در متلب حل کنیم:

$$\large \begin {aligned} \int _ { - 6 } ^ { 6 } { x } ^ { 2 } {d x} & = \left [ \frac { x ^ { 3 } } { 3 } \right ] _{ - 6} ^ { 6 } \\ & = 7 2 - ( - 7 2 ) \\ & = 1 4 4 \end {aligned}$$

بدین منظور، کد زیر را در متلب می‌نویسیم:

1clear all;close all;
2
3% Area under a graph Simple Example and plot it
4
5% declare function and plot it
6syms x
7plot_range = [-10,10];
8
9f = x^2;
10
11%f= -x^2 + 100;
12ezplot(f, plot_range);
13
14hold on;
15
16% define definite integral limits
17int_limits =  [-6  6];
18
19% Integrate
20
21intf = int(f)  % Indefinite Integral
22
23% Definite Integral via Indefinite result
24int_val_ind = int(f,int_limits(1),int_limits(2))
25 
26
27% Idiot Check! Definite Integral via Indefinite result
28subs(intf,int_limits(2)) - subs(intf,int_limits(1))
29% not really a necessary bit of code as Def. Int is the way to do it!
30
31% Set up plot
32range = int_limits(1):0.1:int_limits(2);
33y = subs(f,range); %sample values on curve
34
35% Shade area below the curve
36area(range,y, 'FaceColor',[0, 0, 1], 'LineStyle', 'none');
37
38axis tight;

نتیجه حاصل از اجرای این برنامه به صورت زیر است:‌

intf =
x^3/3
 
int_val_ind =
144
 
ans =
144

مثال چهارم انتگرال معین در متلب

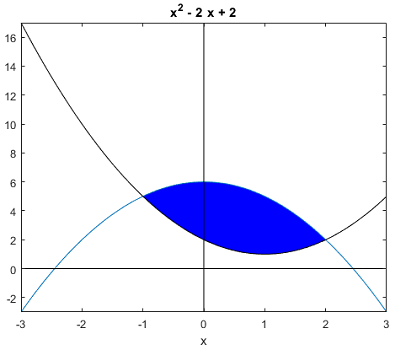
در این مثال، می‌خواهیم محصور بین نمودار دو تابع $$f _ 1 ( x) = - x ^ 2 + 6$$ و $$f _ 2 ( x) = x ^ 2 - 2 x + 2$$ را در بازه $$[-1, 2 ]$$ به دست آوریم.

$$\large \begin {aligned} \text {Area} & = \int _ { - 1 } ^ { 2 } \left ( \left(-x ^ { 2 }+ 6 \right ) - \left ( x ^ { 2 } - 2 x + 2 \right ) \right ) d x \\ & = \int _ { - 1 } ^ { 2 } \left ( - 2 x ^ { 2 } + 2 x + 4 \right ) d x \\ & = \left [ - \frac { 2 } { 3 } x ^ { 3 } + x ^ { 2 } + 4 x \right ] _ { - 1 } ^ { 2 } \\ & = 9 \end {aligned}$$

برنامه زیر، مربوط به محاسبه این مساحت در متلب است که در آن دو تابع از هم کم شده‌اند، سپس از نتیجه انتگرال گرفته شده است:

1clear all;close all;
2
3% Area under a graph Simple Example and plot it
4
5% declare functions
6syms x
7plot_range = [-3,3];
8
9f1 = -x^2 + 6;
10
11f2 = x^2 - 2*x + 2;
12
13% Find max min values over curves for plots
14range = plot_range(1):0.1:plot_range(2);
15y = subs(f1,range); %sample values on curve f1
16
17miny = min(y); %for plot y-axis
18maxy = max(y);
19
20y = subs(f2,range); %sample values on curve f2
21
22if maxy < max(y) maxy = max(subs(y)); end;
23if miny > min(y) miny = min(subs(y)); end;
24
25
26% Find Points of Intersection of curves
27roots_intersect = sort(double(solve (f1 - f2)));
28
29% Definite Integral 
30area_intersect = int(f1 - f2,roots_intersect(1),roots_intersect(2))
31 
32
33% Set up plot
34range = roots_intersect(1):0.1:roots_intersect(2);
35y = subs(f1,range); %sample values on curve f1
36
37
38% Shade Area f1
39area(range,y, 'FaceColor',[0, 0, 1], 'LineStyle', 'none')
40
41hold on;
42
43
44% 'rub out' area above the curve
45y = subs(f2,range); %sample values on curve f2
46area(range,y, 'FaceColor',[1, 1, 1], 'LineStyle', 'none')
47
48% Plot funtions over plot range
49ezplot(f1, plot_range);
50
51hf2 = ezplot(f2, plot_range);
52set(hf2,'Color','black');
53
54
55% plot axes
56plot(plot_range,[0 0], 'k'); % x-axis
57
58plot([0 0],[miny maxy], 'k'); % y-axis
59
60axis tight

جواب حاصل از اجرای این برنامه به صورت زیر است:

area_intersect =
 
9

انتگرال دوگانه در متلب

برای محاسبه انتگرال دوگانه و در کل، انتگرال‌های چندگانه در متلب می‌توانیم از دستور "int" استفاده کنیم.

فرض کنید می‌خواهیم انتگرال زیر را در متلب محاسبه کنیم:

$$\large \int _ 0 ^ 1 \int _ { 1 - x } ^ { 1 - x ^ 2 } \, x y \, d y \, d x$$

می‌توانیم از دستورهای زیر برای این کار استفاده کنیم:

1syms x y
2firstint=int(x*y,y,1-x,1-x^2)
3answer=int(firstint,x,0,1)

یا

1int(int(x*y,y,1-x,1-x^2),x,0,1)

که جواب هر دو $$1/24$$ است.

همچنین، برای انتگرال دوگانه می‌توانیم از دستور "integral2" نیز استفاده کنیم. این دستور به صورت "(integral2(fun,xmin,xmax,ymin,ymax" نوشته می‌شود که در آن، fun تابع و xmin و xmax و ymin و ymax محدوده‌های دو متغیر هستند. توجه کنید که عملگرهای مورد استفاده باید با "." باشند، مثلاً به جای "*" باید از "*." استفاده کرد. همچنین برای تعریف متغیرهای مستقل از "@" استفاده می‌شود. به مثال زیر توجه کنید.

برای مثال، تابع زیر را در نظر بگیرید:

$$\large f (x,y) = \sin x \sin y$$

می‌خواهیم انتگرال دوگانه $$\iint f (x,y ) dx dy$$ را در بازه $$[0, \pi]$$ هم برای $$x$$ و هم برای $$y$$ محاسبه کنیم. بدین منظور، دستور ساده زیر را می‌نویسیم:

1z=@(x,y) sin(x).*sin(y);
2integral2(z,0,pi,0,pi)

که جواب آن برابر با ۴ خواهد بود.

انتگرال عددی در متلب

برای محاسبه انتگرال عددی، دو روش اصلی سیمپسون و ذوزنقه‌ای وجود دارد. برای استفاده از روش سیمپسون، می‌توانید از تابع "(simpsons(f,a,b,n" که کد آن در ادامه آمده است، استفاده کنید. در این برنامه، f تابع مورد نظر است که مثلاً به صورت (f=@(x) sin(x تعریف می‌شود، همچنین a ابتدای بازه انتگرال‌گیری و b انتهای آن است. n نیز که یک عدد صحیح مثبت است، تعداد زیربازه‌های انتگرال‌گیری را مشخص می‌کند. برای آشنایی بیشتر با روش سیمپسون، می‌توانید مطلب «قاعده سیمپسون — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را مطالعه کنید.

1function I = simpsons(f,a,b,n)
2% This function computes the integral "I" via Simpson's rule in the interval [a,b] with n+1 equally spaced points
3% 
4% Syntax: I = simpsons(f,a,b,n)
5% 
6% Where,
7%  f= can be either an anonymous function (e.g. f=@(x) sin(x)) or a vector
8%  containing equally spaced values of the function to be integrated
9%  a= Initial point of interval
10%  b= Last point of interval
11%  n= # of sub-intervals (panels), must be integer
12% 
13%  Written by Juan Camilo Medina  - The University of Notre Dame
14%  09/2010 (copyright Dr. Simpson)
15% 
16% 
17% Example 1:
18% 
19% Suppose you want to integrate a function f(x) in the interval [-1,1].
20% You also want 3 integration points (2 panels) evenly distributed through the
21% domain (you can select more point for better accuracy).
22% Thus:
23%
24% f=@(x) ((x-1).*x./2).*((x-1).*x./2);
25% I=simpsons(f,-1,1,2)
26% 
27% 
28% Example 2:
29% 
30% Suppose you want to integrate a function f(x) in the interval [-1,1].
31% You know some values of the function f(x) between the given interval,
32% those are fi= {1,0.518,0.230,0.078,0.014,0,0.006,0.014,0.014,0.006,0}
33% Thus:
34%
35% fi= [1 0.518 0.230 0.078 0.014 0 0.006 0.014 0.014 0.006 0];
36% I=simpsons(fi,-1,1,[])
37%
38% note that there is no need to provide the number of intervals (panels) "n",
39% since they are implicitly specified by the number of elements in the
40% vector fi
41if numel(f)>1 % If the input provided is a vector
42    n=numel(f)-1; h=(b-a)/n;
43    I= h/3*(f(1)+2*sum(f(3:2:end-2))+4*sum(f(2:2:end))+f(end));
44else % If the input provided is an anonymous function
45    h=(b-a)/n; xi=a:h:b;
46    I= h/3*(f(xi(1))+2*sum(f(xi(3:2:end-2)))+4*sum(f(xi(2:2:end)))+f(xi(end)));
47end

برای استفاده از روش ذوزنقه‌ای نیز از تابع "trapz" در خود متلب استفاده می‌شود. برای مثال، اگر بخواهیم انتگرال $$\sin x$$ را در بازه $$[0 , \pi ]$$، به دست آوریم، داریم:

1X = 0:pi/100:pi;
2Y = sin(X);
3Q = trapz(X,Y)

که جواب آن، $$Q = 1.9998$$ است.

برای آشنایی بیشتر با این روش، پیشنهاد می‌کنیم آموزش «قاعده ذوزنقه ای — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را مطالعه کنید.

انتگرال خطی در متلب

انتگرال خطی در متلب را با یک مثال توضیح می‌دهیم. فرض کنید می‌خواهیم انتگرال زیر را در در متلب محاسبه کنیم:

$$\large \oint _ { C } \frac { e ^ { z } } { z } d z$$

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

که در آن، $$C$$ یک کانتور بسته است که قطب ساده $$e^ z / z$$ را در مبدأ دور می‌زند. ابتدا انتگرالده را به صورت زیر تعریف می‌کنیم:

1fun = @(z) exp(z)./z;

اکنون، به دو روش می‌توانیم انتگرال مورد نظر را حل کنیم.

در روش اول، می‌توانیم انتگرال‌های خطی توابع مختلط را با یک پارامتری سازی ارزیابی کنیم. در این صورت، یک کانتور مشخص شده است و سپس برای پارامتری کردن انتگرالده اصلی از آن مشتق گرفته می‌شود. برای این مثال، کانتور را به عنوان دایره واحد در نظر می‌گیریم، اما در همه موارد، نتیجه مستقل از کانتور انتخاب شده است. بنابراین، داریم:

1g = @(theta) cos(theta) + 1i*sin(theta);
2gprime = @(theta) -sin(theta) + 1i*cos(theta);
3q1 = integral(@(t) fun(g(t)).*gprime(t),0,2*pi)

که جواب آن به صورت زیر است:

q1 = -0.0000 + 6.2832i

این روش پارامتری سازی اگرچه قابل اعتماد است، اما دشوار و وقت‌گیر نیز هست، زیرا یک مشتق باید قبل از انجام انتگرال‌گیری محاسبه شود. حتی برای توابع ساده نیز باید چندین خط کد بنویسیم. از آنجا که نتیجه با هر کانتور بسته که قطب را محصور می‌کند یکسان است، می‌توانیم از روش دوم که همان دستور  "waypoints" استفاده کنیم که برای ساختن یک مسیر مربع یا مثلثی است که قطب را محصور می‌کند.

اگر حدود انتگرال یا عناصر بردار مختلط باشند، دستور "integral" انتگرال‌گیری را روی دنباله‌ای از مسیرهای خطی در صفحه مختلط انجام می‌دهد. جهت طبیعی یک کانتور خلاف جهت عقربه‌های ساعت است. مشخص کردن یک کانتور در جهت عقربه‌های ساعت متناظر با ضرب انتگرال در $$-1$$ است. کانتور را به گونه‌ای مشخص می‌کنیم که یک تکینگی را محصور کند. اگر کانتوری را مشخص کنیم که هیچ قطبی را محصور نکند، در این صورت قضیه انتگرال کوشی تضمین می‌کند که مقدار انتگرال مسیر بسته صفر است.

برای بررسی این موضوع، از تابع "fun" حول یک مسیر مربع به دور از مبدأ انتگرال می‌گیریم. برای ایجاد یک کانتور بسته، از حدود مشابه برای انتگرال‌گیری استفاده می‌کنیم.

1C = [2+i 2+2i 1+2i];
2q = integral(fun,1+i,1+i,'Waypoints',C)

که جواب آن $$q2 = -0.0000 + 6.2832i$$ است. این نتیجه، مشابه نتیجه حاصل از روش اول بوده و مقدار دقیق آن $$2 \pi i$$ است.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌ های برنامه‌‌ نویسی
• مجموعه آموزش های برنامه‌نویسی متلب (MATLAB)
• مجموعه آموزش‌های پروژه محور برنامه‌نویسی
• مجموعه آموزش های برنامه‌نویسی متلب برای علوم و مهندسی
• منابع آموزشی نرم افزار متلب و برنامه نویسی کاربردی با آن
• زبان برنامه نویسی پایتون (Python) — از صفر تا صد
• تقلب نامه (Cheat Sheet) توابع و دستورات متلب (MATLAB)

^^