استوکیومتری گازها – به زبان ساده

مقدمه‌ای بر استوکیومتری گازها

چگالی گازها

می‌دانیم که چگالی عبارتست از نسبت جرم به حجم و همین رابطه برای گازها نیز صادق است:

$$\rho = \frac {m} {V}$$

بنابراین، در مسائل استوکیومتری گازها اگر بتوانیم حجم گازها را تعیین کنیم، تعیین چگالی آن‌ها کار ساده‌ای خواهد بود. همچنین، از چگالی یک گاز می‌توان برای تعیین جرم مولی و به دنبال آن، تعیین نوع گاز استفاده کرد. همانطور که در بالا نیز به آن اشاره شد، به کمک قانون گازهای ایده‌آل، رابطه‌ای بدست می‌آوریم که چگالی یک گاز را به حجم آن در مسائل مربوط به استوکیومتری گازها نسبت دهد. این رابطه را در مثال زیر بررسی خواهیم کرد.

مثال 1

به کمک رابطه $$P V = n R T$$، فرمولی برای دانسیته گازها به صورت g/L بدست بیاورید.

$$P V = n R T$$

$$\begin{equation} \frac {n} {V} = \frac { P } { R T } \end{equation}$$

دو طرف معادله را در جرم مولی $$(\mathcal{M})$$ ضرب می‌کنیم. از آن‌جایی که واحد جرم مولی به صورت g/mol است، واحد گرم که به آن نیاز داشتیم در فرمول پدیدار می‌شود.

$$\begin{equation} \begin{aligned} &(\mathcal{ M }) \left(\frac { n } { V } \right) = \left(\frac{ P }{ R T } \right) (\mathcal{M})\\ &g / \mathbf { L } = \rho = \frac{P \mathcal { M }} { R T } \end{aligned} \end{equation}$$

حال، این معادله را در مثالی دیگر ارزشیابی می‌کنیم:

$$\rho = \frac {P M} {R T}$$

$$\begin{equation} \begin{aligned} &0.0847 \mathrm{g} / \mathrm{ L } = 760 \text { torr } \times \frac{ 1 \text { atm }} {760 \mathrm {torr}} \times \frac { M }{ 0.0821 \mathrm { L } \text { atm } / \mathrm{ mol } \ \mathrm { K } } \times 290 \mathrm { K } \end{aligned} \end{equation}$$

$$\mathcal{M} = 2.202 g/mol$$

مثال 2

فیلم آموزش حل مسائل استوکیومتری و تهیه محلول‌ها در فرادرس

کلیک کنید

$$\begin{equation} \begin{aligned} &85.7 \mathrm{g} \mathrm{C} \times \frac{1 \mathrm{mol} \mathrm { C }} { 12.01 \mathrm{ g C }} = 7.136 \mathrm { m o l} \mathrm { C } \frac {7 .136} {7.136} = 1 .00 \mathrm{ m o l } \mathrm{ C } \\ &14.3 \mathrm { g } \mathrm { H } \times \frac {1 \mathrm { m o l } \mathrm { H }} {1.01 \mathrm{ g } \mathrm { H } } = 1 4 . 1 5 8 \mathrm { m ol } \mathrm { H } \frac { 1 4.158}{7.136} = 1.98 \mathrm { m o l } \mathrm { H } \end{aligned} \end{equation}$$

با توجه به اعداد بدست آمده، در می‌یابیم که فرمول تجربی، $$C H _ 2$$ خواهد بود. جرم حاصل از فرمول تجربی (EM) نیز برابر با 14/03 خواهد بود. در ادامه، به کمک رابطه مثال قبل، چگالی را محاسبه می‌کنیم:

$$\begin{equation} \mathrm{\rho} = \frac{\mathrm { P M }} {\mathrm{ R T }} \frac{ 1 .5 6 \mathrm { g } } { 1.00 \mathrm { L } } = 0.984 \mathrm { a t m } \times \frac { M } { 0.0821 \mathrm { L } \mathrm { a tm } / \mathrm { m o l } \mathrm { K } } \times 323 \mathrm { K } \end{equation}$$

$$\begin{equation} \mathscr { M } = 42.0 \mathrm{ g } / \mathrm{ m o l } \\ \frac {\mathcal { M } } {\mathrm { E } \mathcal { M } } = \frac{ 4 2 . 0 } {14.03} = 2 . 99 \Rightarrow (3) \\ 3 \times \left (\mathrm { C H } _ { 2 } \right) = \mathrm{ C } _ { 3 } \mathrm { H } _ { 6 } \end{equation}$$

جرم مولی یک گاز

از کاربردهای دیگر رابطه گاز ایده‌آل، تعیین جرم مولی است. بنا به تعریف، جرم مولی یک ماده، نسبت جرم ماده (گرم) به تعداد مول‌های آن ذکر می‌شود.

$$\mathcal { M } = \frac{m}{n}$$

$$n = \frac {P V } {R T }$$

$$\begin{equation} \mathcal { M } = \frac { m R T } { P V } \end{equation}$$

از رابطه بالا می‌توان برای محاسبه جرم مولی گازها به کمک مقادیر فشار، حجم، دما و جرم گاز کمک گرفت.

مثال: تعیین جرم مولی یک مایع فرار

جرم مولی یک مایع فرار را به کمک مراحل زیر می‌توان محاسبه کرد:

• حرارت دادن نمونه مایع در بالون حجمی دربسته، که سوراخی روی دهانه آن ایجاد شده باشد. این کار موجب خروج گاز خواهد شد.
• زمانی تمامی مایع به گاز تبدیل شد، حرارت دادن را به سرعت متوقف می‌کنیم. در این زمان، نمونه در فشار محیط،‌ تنها توسط گاز، پر شده است.
• با عایق کردن بالون حجمی، به گاز فرصت می‌دهیم تا میعان کند. در ادامه، وزن نهایی بالون را اندازه‌گیری می‌کنیم تا به کمک آن، جرم نمونه مشخص شود.

به کمک دستورالعمل بالا، جرم نمونه‌ای از گاز کلروفرم در دمای 99/6 درجه سانتی‌گراد و حجم 129 سانتی‌متر مکعب، برابر با 0/494 گرم اندازه‌گیری شده که در این شرایط، فشار اتمسفری برابر با 742/1 میلی‌متر جیوه ذکر شده است. مقدار تقریبی جرم مولی کلروفرم را محاسبه کنید.

$$\begin{equation} \mathcal { M } = \frac { m R T } { P V } \end{equation}$$

$$\begin{equation} \mathcal { M } = \frac {m R T } {P V} = \frac {(0.494 \mathrm { g }) \times 0.08206 \mathrm {L.} \text { atm } / \mathrm { mol } \mathrm { K } \times 372.8 \mathrm { K } } { 0.976 \mathrm { a tm } \times 0.129 \mathrm { L } } = 120 \mathrm { g } / \mathrm { m o l } \end{equation}$$

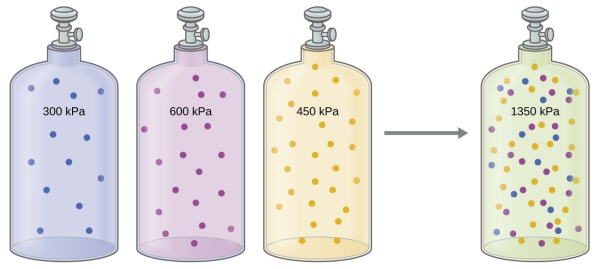
فشار مخلوط گازها: قانون دالتون

در محاسبات استوکیومتری گازها و به طور کلی، تا زمانی که گازها در یک مخلوط گازی با یکدیگر وارد واکنش نشوند، تاثیری بر فشار یکدیگر نخواهند داشت. به عبارت دیگر،‌ هر گاز در یک مخلوط گازی، همان فشاری را خواهد داشت که به تنهایی در یک مخزن جدا ایجاد می‌کند.

فیلم آموزش حل مسائل استوکیومتری در فرادرس

کلیک کنید

$$\begin{equation} P _ {T o t a l} = P _ { A } + P _ { B } + P _ { C } + \ldots = \Sigma _ { i } P _ { i } \end{equation}$$

کسر مولی

$$P _ A = \chi _ A \times P _ {total}\\ \chi _ A = \frac {n _ a}{n _ {total}}$$

در رابطه بالا، $$P_A$$، $$X_A$$ و $$n_A$$ به ترتیب، فشار جزئی، کسر مولی و تعداد مول‌های گاز A خواهند بود.

مثال

یک مخلوط گازی شامل 2/83 مول گاز اکسیژن و 8/41 مول گاز نیتروس اکسید $$N_2O$$ و فشار کل مخلوط برابر با 192 کیلوپاسکال است.

• کسر مولی $$O _ 2$$ و $$N_2O$$ را حساب کنید.
• فشار جزئی این دو گاز را حساب کنید.

محاسبات برای $$O _ 2$$:

$${X} _ { { O } _ { 2 }} = \frac { { n } _ { { O } _ { 2 } } } { { n }_ { Total } } = \frac { \text {2.83 mol}} { \left (2.83 + 8.41 \right ) \text {mol } } = 0.252$$

$${ P } _ { { O } _ { 2 } } = { X } _ {{ O } _ { 2 } } \times { P } _ {Total} = 0.252 \times \text { 1 9 2 kPa } = \text {48.4 kPa}$$

محاسبات برای $$N_2O$$:

$${ X } _ { { O } _ { 2 }} = \frac { { n } _ { { O } _ { 2 } } } { { n } _ {Total} } = \frac { \text {2.83 mol} } {\left (2.83 + 8.41 \right ) \text { mol } } = 0.252$$

$${ P } _ { { O } _ { 2 } } = { X } _ {{ O } _ { 2 } } \times { P } _ {Total } = \left (0.252 \right ) \times \text { 192 kPa }$$

$${ P } _ {{ O } _ { 2 } } = { X } _ { { O } _ { 2 }}\times { P } _ { Total } = 0.252 \times \text {192 kPa} = \text {48.4 kPa}$$

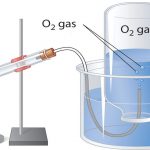
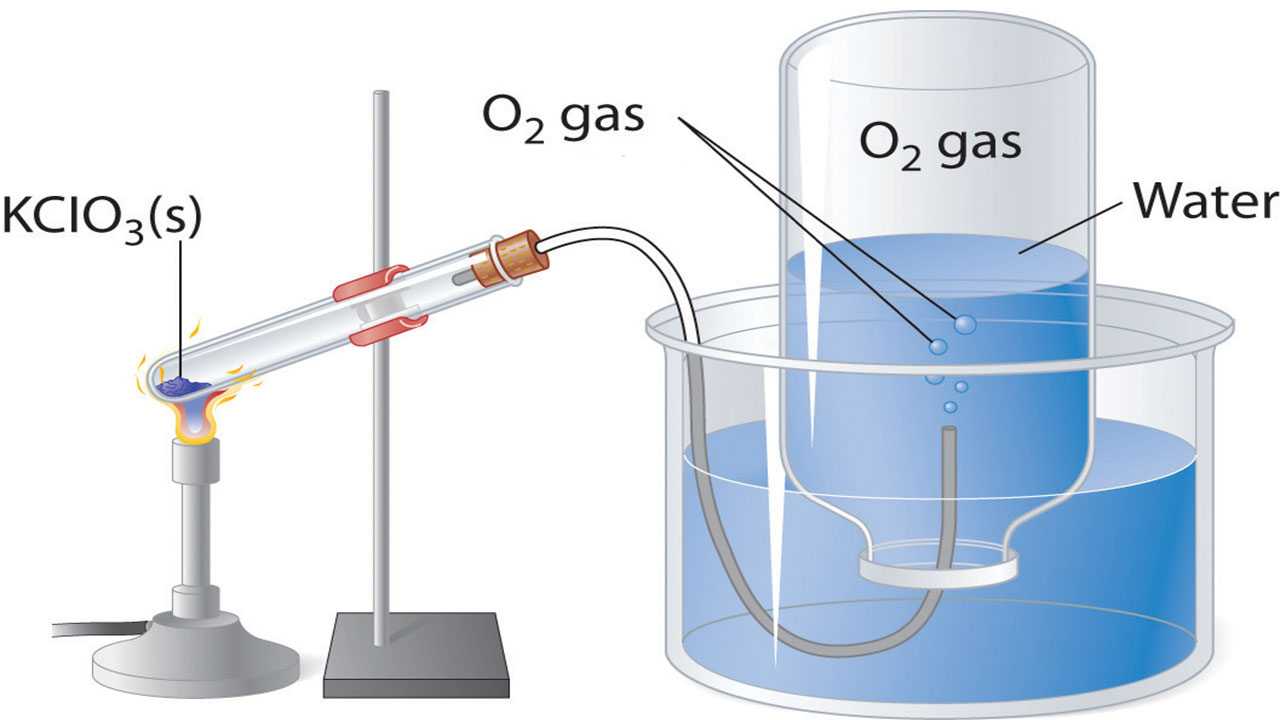
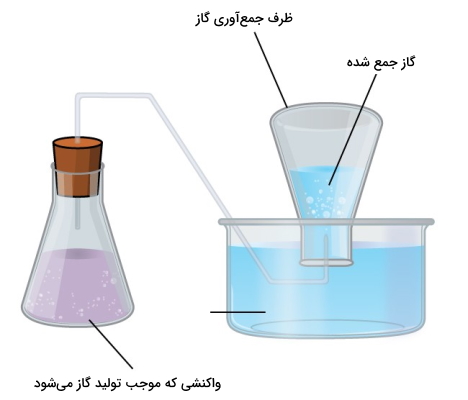
جمع‌آوری گاز بالای آب

البته در استوکیومتری گازها عامل دیگری را نیز باید به هنگام اندازه‌گیری فشار گاز با این روش در نظر گرفت. آب تبخیر خواهد شد و همواره بخار آبی بالای ظرف آب خواهیم داشت. همزمان با جمع شدن گاز، بالای آب، فشاری معادل مجموع فشارهای جزئی گاز و بخار آب بوجود می‌آید. بنابراین، فشار گاز خالص، برابر با فشار کل منهای فشار بخار آب خواهد بود. این فشار به فشار گاز خشک معروف است. فشار بخار آب نیز به دمای آن بستگی دارد.

مثال

اگر 0/2 لیتر آرگون، در بالای آب با دمای 26 درجه سانتی‌گراد و فشار $$750 torr$$ جمع آوری شود، مقدار فشار جزئی آرگون را محاسبه کنید.

بر اساس قانون دالتون، فشار کل $$750 torr$$، برابر با مجموع فشار جزئی آرگون و فشار بخار آب خواهد بود.

$$\begin{equation} P _ { \mathrm { T } } = P _ { \mathrm { A r }} + P _ {\mathrm { H } _ { 2 } \mathrm { O } } \end{equation}$$

$$\begin{equation} P _ { \mathrm { A r } } = P _ { \mathrm { T } } - P _ { \mathrm { H } _ { 2 } \mathrm { O } } \end{equation}$$

با مراجعه به جداول فشار بخار در می‌یابیم که فشار بخار آب در دمای 26 درجه سانتی‌گراد برابر با $$25.2 torr$$ است. بنابراین، فشار جزئی آرگون به کمک رابطه زیر محاسبه خواهد شد:

$$\begin{equation} P _ {\mathrm { A r } } = 750 \text { torr} - 25.2 \text { torr } = 725 \text { torr } \end{equation}$$

محاسبات کمی و استوکیومتری گازها

بازنگری در قانون آووگادرو

فیلم آموزش فرایندهای جداسازی غشایی – مقدماتی در فرادرس

کلیک کنید

$${\text { N } } _ { 2 } \left ( g \right ) + 3 {\text{H} } _ { 2 } \left ( g \right ) \rightarrow { 2 {\text { N H } } } _ { 3 } \left ( g \right)$$

توصیف این قانون،‌ در تصویر زیر قابل ملاحظه است.

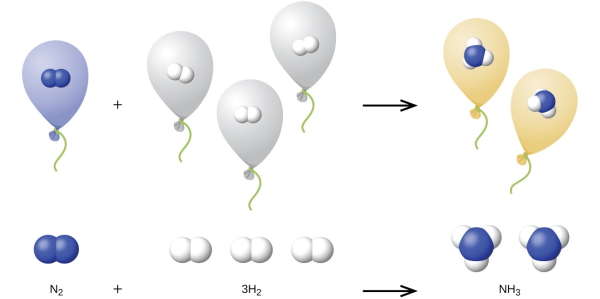
مثال 1

$$\begin{equation} \mathrm { C } _ { 3 } \mathrm { H } _ { 8 }( g ) + \quad 5 \mathrm { O } _ { 2 } (g) \quad \longrightarrow \quad 3 \mathrm { C O } _ { 2 } (g) + 4 \mathrm { H } _ { 2 } \mathrm { O } (l) \end{equation}$$

بنابراین خواهیم داشت:

$$2.7 {\text { L} {\text { C } } _ {3} {\text {H} } _ {8}}\times \frac { \text { 5 L } {\text { O }} _ { 2 }} {1{\text{L} {\text { C}} _ {3} {\text {H} } _ { 8 } } } = \text{13.5 L} {\text {O}} _ { 2 }$$

در نتیجه، 13/5 لیتر گاز اکسیژن برای واکنش با 2/7 لیتر پروپان مورد نیاز خواهد بود.

مثال ۲

$$\begin{equation} \mathrm { N } _ { 2 }( g ) + 3 \mathrm { H } _ { 2 } (g) \rightarrow 2 \mathrm { N H } _ { 3 } (g) \end{equation}$$

واکنش بالا نشان می‌دهد که ۱ حجم از نیتروژن با ۳ حجم از هیدروژن وارد واکنش می‌شود تا ۲ حجم آمونیاک به تولید برسد. در نتیجه، نسبت ۳ به ۲ را برای محاسبات استوکیومتری گازها باید در نظر گرفت:

$$683 {\text{ billion} { \text{ ft} } ^ {3} {\text {N H} } _ {3}} \times \frac {\text {3 billion } {\text { ft}} ^ { 3 } {\text{ H }} _ {2}} {2 {\text{ billion} {\text { ft}} ^ {3} {\text { N H } } _ {3}}} = 1.02 \times { 10 } ^ { 3 } \text{billion} { \text { ft}} ^ { 3 } { \text {H}} _ { 2 }$$

مثال ۳

در صورت واکنش 8/88 گرم $$Ga$$ با مقدار اضافی هیدروکلریک اسید در دمای 27 درجه سانتی‌گراد و فشار $$723Torr$$، چه حجم گاز هیدروژن به تولید می‌رسد.

$$\begin{equation} 2 \mathrm { G a } (s) + 6 \mathrm { H C l } (a q) \rightarrow 2 \mathrm { Ga Cl } _ { 3 } ( a q ) +3 \mathrm {H} _ { 2 } ( g ) \end{equation}$$

برای این‌که جرم گالیم را به حجم گاز هیدروژن تبدیل کنیم، باید مراحل زیر طی شود:

حجم گاز هیدرژون $$\rightarrow$$ تعداد مول گاز هیدروژن $$\rightarrow$$ تعداد مول گالیم $$\rightarrow$$ جرم گالیم

$$8.88{ \text {g Ga} } \times \frac{ 1 {\text {mol Ga}}}{69.723{ \text{ g Ga }}} \times \frac {\text { 3 mol } { \text { H} } _ {2}} {2 {\text {mol Ga} } } = 0.191{ \text {mol H}} _ { 2 }$$

حال، از قانون گازهای ایده‌آل برای حل قسمت آخر استفاده می‌کنیم:

$${ V } _ {{ \text{H} } _ { 2 } } = {\left ( \frac {n R T } {P } \right) } _ { {\text{H}} _ { 2 }} = \frac { 0.191 {\text {mol}} \times \text {0.08206 L} {\text {atm} { \text {mol} } ^ { - \text {1} }{\text {K} } ^ { - \text {1} } } \times \text {300 K}}{0.951 {\text {atm} }} = \text {4.94 L }$$

اگر این مطلب برای شما مفید بوده‌ است،‌ آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس شیمی
• مجموعه آموزش‌های مهندسی شیمی
• آموزش شیمی عمومی
• گاز واقعی (حقیقی) — از صفر تا صد
• قانون بویل — به زبان ساده

^^