تحلیل تنش های برشی در تیرهای مستطیلی – با مثال های کاربردی

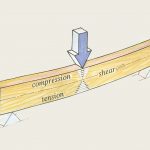
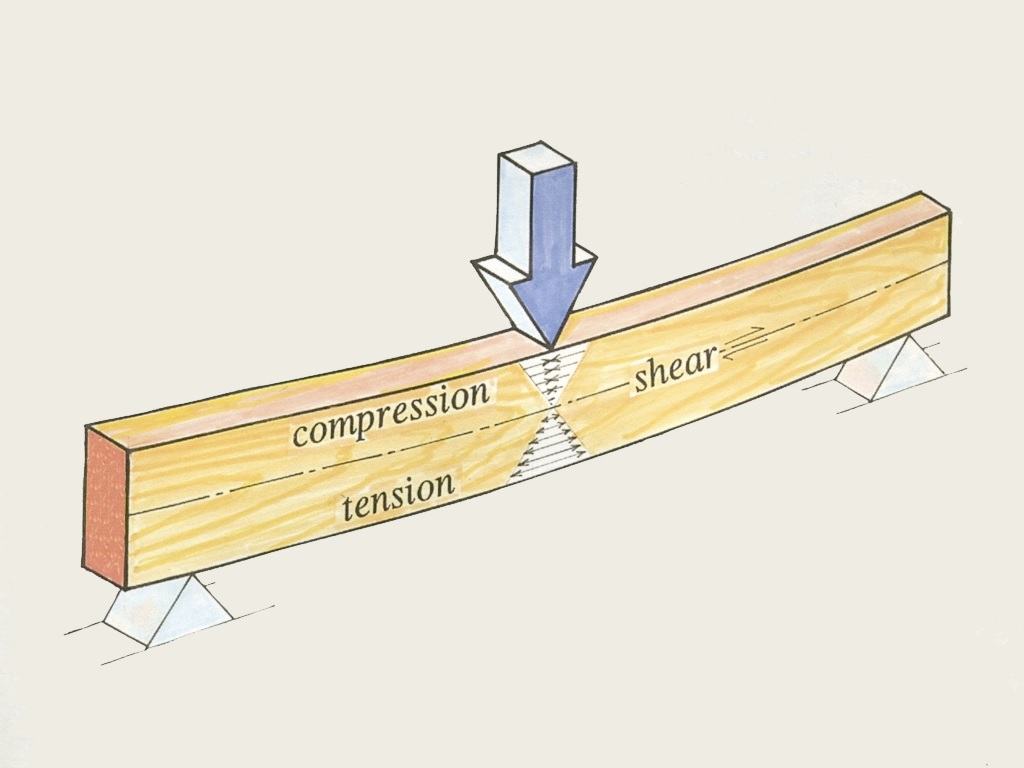
در مبحث «خمش خالص و خمش غیر یکنواخت»، با دو مفهوم اساسی در حوزه خمش آشنا شدیم. اگر یک تیر در معرض خمش خالص قرار داشته باشد، گشتاورهای خمشی به عنوان برآیندهای تنش در نظر گرفته شده و تنش‌های نرمال بر روی مقاطع عرضی اعمال می‌شوند. با این وجود، اکثر تیرها در معرض بارگذاری‌هایی با مؤلفه‌های گشتاورهای خمشی و تنش‌های برشی (خمش غیریکنواخت) قرار دارند. در این موارد، تنش‌های نرمال و برشی با هم درون تیر توسعه می‌یابند. اگر تیر از مواد الاستیک خطی ساخته شده باشد، تنش‌های نرمال با استفاده از رابطه پیچش قابل محاسبه خواهند بود. در این مقاله، مراحل تعیین مؤلفه‌های تنش برشی، محاسبه گشتاور اول و مشخص کردن نحوه توزیع این نوع تنش‌ها در تیرهای مستطیلی (تیرهایی با سطح مقطع مستطیلی شکل) را مورد بررسی قرار خواهیم داد. در انتها نیز به تشریح چند مثال کاربردی خواهیم پرداخت.

تنش برشی افقی و عمودی

شکل زیر، تنش‌های برشی موجود در یک تیر با مقطع مستطیل (عرض b و ارتفاع h) را در حین اعمال نیروی برشی و مثبت V نمایش می‌دهد. با توجه به پیکربندی این تیر می‌توان تنش‌های برشی اعمال شده بر روی مقطع عرضی (τ) را موازی با نیروی برشی V (بخش عمودی مقطع) در نظر گرفت.

علاوه بر این، فرض یکنواخت بودن توزیع تنش‌های برشی در راستای عرض تیر نیز منطقی به نظر می‌رسد. اگرچه، این توزیع بر روی ارتفاع سازه تغییر می‌کند. با به کارگیری این دو فرض، امکان تعیین شدت تنش برشی در هر نقطه دلخواه بر روی مقطع عرضی فراهم می‌شود.

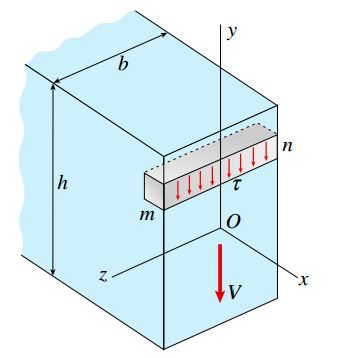
به منظور اجرای تحلیل، یک المان کوچک از تیر بالا (mn) را در نظر بگیرید. این المان در فاصله بین دو مقطع عرضی و دو صفحه افقی مجاور قرار دارد. فرض کنید که تنش برشی اعمال شده بر روی صفحه جلویی المان به صورت عمودی و توزیع آن در راستای تیر یکنواخت است. به خاطر داشته باشید که اعمال تنش‌های برشی بر روی هر یک از صفحات المان باعث به وجود آمدن تنش‌های برشی هم‌اندازه بر روی صفحات عمودی می‌شود (برابری تنش‌های برشی بر روی صفحات عمود). این موضوع در شکل زیر نیز قابل مشاهده است. از این‌رو، به همراه تنش‌های برشی عمودی موجود بر روی مقاطع عرضی، تنش‌های برشی افقی در میان لایه‌های افقی تیر به وجود می‌آیند. برای هر نقطه درون تیر، تنش‌های برشی مکمل دارای مقدار برابر هستند.

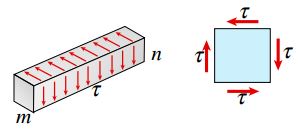
با در نظر گرفتن برابری بین مقادیر تنش‌های برشی عمودی و افقی اعمال شده بر روی یک المان می‌توان به مسئله مهمی در مورد تنش‌های موجود در بالا و پایین تیر دست یافت. اگر المان mn بخش بالایی یا پایینی تیر را مورد تحلیل قرار دهیم، به دلیل عدم وجود تنش بر روی سطوح خارجی تیر، تنش‌های برشی افقی از بین می‌روند. علاوه بر این، تنش‌های برشی عمودی موجود در این نواحی نیز متعاقباً ناپدید می‌شوند. به عبارت دیگر در نقاط y=±h/2، مقدار تنش برشی τ=0 خواهد بود.

وجود تنش‌های برشی افقی در یک تیر را می‌توان با استفاده از یک آزمایش ساده نمایش داد. به این منظور باید دو تیر یکسان با مقطع مستطیلی را مطابق شکل زیر بر روی تکیه‌گاه‌های ساده قرار دهیم و نیروی متمرکز P را به آن‌ها اعمال کنیم.

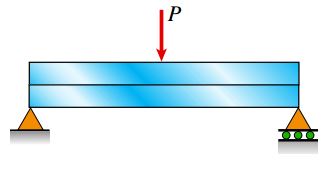
اگر اصطکاک بین دو تیر کم باشد، هر یک از آن‌ها به صورت مستقل خم خواهند شد (شکل زیر). این تیرها در بالای محور خنثی خود تحت فشار و در پایین این محور تحت کشش قرار دارند. به این ترتیب، سطح زیرین تیر بالایی نسبت به سطح بالایی تیر پایینی لغزش خواهد داشت.

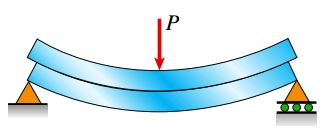
اکنون فرض کنید که سطوح این دو تیر با استفاده از چسب به هم وصل شده و یک تیر واحد را تشکیل داده‌اند. هنگامی که این تیر واحد در معرض بارگذاری قرار گیرد، تنش‌های برشی افقی در سراسر سطح اتصال توسعه می‌یابند. این تنش‌ها برای جلوگیری از لغزش نمایش داده شده در شکل بالا به وجود می‌آیند. وجود این تنش‌های برشی باعث افزایش صلبیت و مقاومت تیر واحد نسبت به دو تیر مجزا می‌شود.

رابطه برش

در این بخش، رابطه‌ای را برای تعیین تنش‌های برشی τ در یک تیر با مقطع مستطیل می‌پردازیم. بررسی تنش‌های برشی افقی موجود در میان لایه‌های یک تیر ساده‌تر از ارزیابی تنش‌های برشی عمودی اعمال شده بر روی یکی از مقاطع آن است.

برای شروع کار، تیر نمایش داده شده در شکل زیر را در نظر بگیرید. همان‌گونه که مشاهده می‌کنید، این تیر تحت خمش غیر یکنواخت قرار دارد. در مرحله بعد، دو مقطع عرضی mn و m₁n₁ که نسبت به یکدیگر دارای فاصله dx را در نظر بگیرید. در فاصله میان این دو مقطع، المان mm₁n₁n تشکیل می‌شود. گشتاور خمشی و نیروی برشی اعمال شده بر روی صفحه سمت چپ این المان به ترتیب با حروف M و V علامت‌گذاری شده‌اند. امکان تغییر گشتاور خمشی و نیروی برشی بر روی محور تیر وجود دارد. به همین دلیل، کمیت‌های صفحه سمت راست المان با عبارت‌های M+dM و V+dV علامت‌گذاری می‌شوند.

به دلیل وجود گشتاورهای خمشی و تنش‌های برشی در شکل بالا، هر دو سطح المان مورد تحلیل تحت تنش‌های نرمال و برشی قرار خواهند داشت. با این وجود، به منظور تعیین رابطه برش فقط به تنش‌های نرمال نیاز خواهد بود. از این‌رو، در شکل زیر تنها وضعیت تنش‌های نرمال موجود در المان mm₁n₁n نمایش داده شده است.

تنش‌های نرمال موجود بر روی مقاطع عرضی mn و m₁n₁ به ترتیب برابرند با:

و

روابط بالا مشابه رابطه خمش هستند. در این روابط، y، فاصله از محور خنثی و I، ممان اینرسی سطح مقطع عرضی حول محور خنثی را نمایش می‌دهند. در مرحله بعد، صفحه افقی pp₁ را از درون المان mm₁n₁n عبور می‌دهیم تا المان کوچک‌تر mm₁p₁p مطابق شکل زیر به وجود آید. صفحه pp₁ به اندازه y₁ از سطح خنثی تیر فاصله دارد. توجه داشته باشید که به دلیل انطباق سطح بالایی mm₁p₁p بر روی سطح بالایی تیر، هیچ تنشی بر روی این صفحه وجود نخواهد داشت. با این وجود، سطح پایینی المان mm₁p₁p در معرض تنش برشی افقی τ قرار می‌گیرد. مقاطع عرضی mp و m₁p₁ نیز به ترتیب تنش‌های خمشی σ₁ و σ₂ را تحمل می‌کنند. این تنش‌ها توسط گشتاورهای خمشی به وجود می‌آیند. علاوه بر این، تنش‌های برشی عمودی نیز بر روی مقطع عرضی مذکور اعمال می‌شوند اما هیچ تأثیری بر روی تعادل المان mm₁p₁p در راستای افقی (بر روی محور x) نمی‌گذارند.

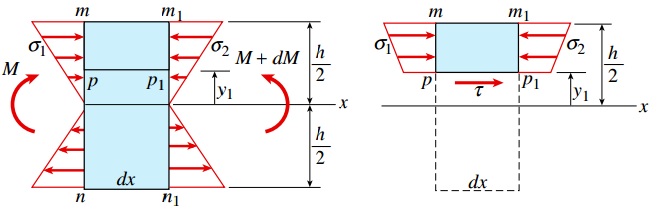
اگر گشتاورهای خمشی اعمال شده در مقاطع عرضی mn و m₁n₁ با هم برابر باشند (تیر تحت خمش خالص قرار داشته باشد)، تنش‌های نرمال σ₁ و σ₂ بر روی صفحات mp و m₁p₁ نیز با هم برابر خواهند بود. در این شرایط، المان mm₁p₁p هنگام اعمال تنش‌های نرمال در حالت تعادل قرار می‌گیرد. به این ترتیب، تنش‌های برشی τ از روی صفحه پایینی pp₁ حذف می‌شوند. این وضعیت با شرایط تیر تحت خمش خالص مطابقت دارد؛ چراکه در این حالت بارگذاری نیز هیچ نیروی تنشی (در نتیجه هیچ تنش برشی) بر روی تیر اعمال نمی‌شود. در صورتی که گشتاورهای خمشی در امتداد محور x تغییر کنند (حالت خمش غیر یکنواخت)، تنش برشی τ اعمال شده بر روی سطح پایینی المان mm₁p₁p با استفاده از معادلات تعادل در راستای محور x قابل محاسبه خواهد بود. به این منظور، ابتدا المان سطح dA در فاصله y از محور خنثی را در نظر می‌گیریم (شکل زیر).

نیروی اعمال شده بر روی این المان برابر با σdA است. پارامتر σ، تنش نرمال را نمایش می‌دهد. این تنش با استفاده از رابطه خمش به دست می‌آید. اگر المان سطح مورد بررسی بر روی سطح سمت چپ mm₁p₁p قرار داشته باشد (جایی که گشتاور خمشی برابر با M است)، تنش نرمال با استفاده از رابطه σ₁=-My/I قابل محاسبه خواهد بود. به این ترتیب، برای المان نیرو داریم:

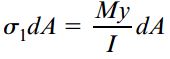
توجه داشته باشید که در معادله بالا تنها از قدر مطلق مقادیر استفاده شده است؛ چراکه جهت تنش‌ها بر روی شکل مشخص هستند. با جمع المان‌های نیرو موجود بر روی سطح mp، نیروی افقی کل F₁ به دست می‌آید:

محدوده انتگرال بالا بر روی سطح پر رنگ (از y=y₁ تا y=h/2) قرار دارد. در شکل زیر، نیروی F₁ بر روی یک نمودار جسم آزاد نمایش داده شده است (از نیروهای عمودی صرف‌نظر شده است).

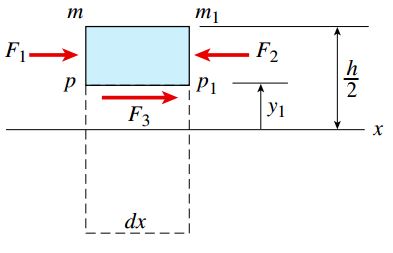
به همین ترتیب، نیروی کل F₂ بر روی سطح راست المان (m₁p₁) نیز به دست می‌آید:

با تعیین نیروهای F₁ و F₂، نیروی افقی اعمال شده بر سطح پایینی المان mm₁p₁p را محاسبه می‌کنیم. از آنجایی که این المان در حالت تعادل قرار دارد، جمع نیروهای موجود در راستای محور x را به دست می‌آوریم. به این ترتیب داریم:

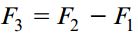
یا

کمیت‌های dM و I بر روی هر سطح مقطع دلخواه دارای مقادیر ثابت هستند. به همین دلیل، این کمیت‌ها را می‌توان از انتگرال خارج کرد. به این ترتیب، رابطه F₃ به صورت زیر درمی‌آید:

اگر توزیع تنش‌های برشی τ بر روی عرض تیر یکنواخت باشد، نیروی F₃ برابر است با:

bdx در رابطه بالا، مساحت سطح پایینی المان mm₁p₁p را نمایش می‌دهد. با ترکیب این رابطه با رابطه قبلی و حل آن با توجه به پارامتر τ خواهیم داشت:

کمیت dM/dx همان نیروی برشی V است. از این‌رو، عبارت رابطه بالا به شکل زیر درمی‌آید:

انتگرال موجود در معادله بالا بر روی بخش پر رنگ مقطع گرفته شده است. به همین دلیل، این انتگرال با گشتاور اول سطح مذکور نسبت به محور خنثی برابری می‌کند. به عبارت دیگر، انتگرال بالا، گشتاور اول سطح مقطع بالایی ناحیه‌ای است که تنش برشی بر روی آن مورد ارزیابی قرار می‌گیرد. این گشتاور اول معمولاً با حرف Q نمایش داده می‌شود:

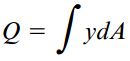
با معرفی مفهوم گشتاور اول، معادله تنش برشی به شکل زیر تبدیل می‌شود:

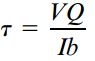
معادله بالا با عنوان «رابطه برش» (Shear Formula) شناخته می‌شود و به منظور تعیین تنش برشی τ در هر نقطه دلخواه بر روی سطح مقطع یک تیر مستطیلی مورد استفاده قرار می‌گیرد. توجه داشته باشید که برای این شکل خاص از سطح مقطع، نیروی برشی V، ممان اینرسی I و عرض b به عنوان کمیت‌های ثابت در نظر گرفته می‌شوند. با این وجود، گشتاور اول Q (و تنش برشی τ) نسبت به فاصله y₁ تا محور خنثی تغییر می‌کند.

اصول محاسبه گشتاور اول Q

معمولاً اگر محل قرارگیری تنش برشی مورد تحلیل مانند شکل زیر در بالای محور خنثی باشد، گشتاور اول سطح مقطع بالای آن محل (ناحیه پررنگ در شکل) مورد محاسبه قرار خواهد گرفت.

اگرچه، برای این کار می‌توان گشتاور اول سطح زیر محل مورد نظر را محاسبه و در علامت منفی ضرب کرد.

گشتاور اول بر روی تمامی یک سطح نسبت به محور خنثی آن برابر با صفر است؛ چراکه محور خنثی از مرکز هندسی سطح مقطع عبور می‌کند. مقدار Q برای ناحیه زیر y₁، منفیِ Q برای ناحیه بالای y₁ خواهد بود. به این ترتیب، برای محاسبه Q در یک نقطه باید به موقعیت آن نسبت به محور خنثی توجه کرد. از آنجایی که جهت اعمال تنش برشی هم‌جهت با نیروی برشی V است؛ توجه به قواعد علامت‌گذاری برای محاسبه V و Q اهمیت چندانی ندارد. برای انجام این محاسبات می‌توان تمام عبارت‌های موجود در رابطه برش را به عنوان کمیت‌های مثبت در نظر گرفت و سپس جهت تنش‌های برشی را مورد تحلیل قرار دارد.

توزیع تنش برشی در یک تیر مستطیلی

در این بخش، نحوه توزیع تنش‌های برشی موجود در یک تیر با سطح مقطع مستطیلی را مورد بررسی قرار می‌دهیم. به این منظور، تیر نمایش داده شده در شکل زیر را در نظر بگیرید.

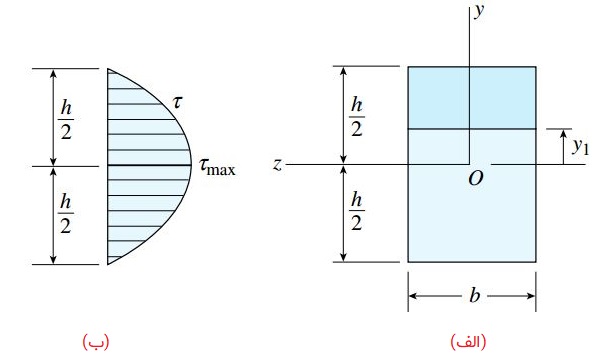
در مرحله اول، گشتاور اول Q ناحیه پررنگ را با ضرب مساحت این بخش از مرکز هندسی تا محور خنثی به دست می‌آوریم:

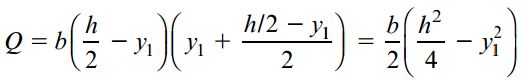
نتیجه بالا با استفاده از انتگرال‌گیری (رابطه Q در بخش قبلی) نیز به دست می‌آید:

با جایگذاری عبارت Q در رابطه برش داریم:

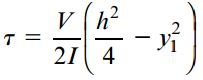
این معادله نشان می‌دهد که تنش‌های برشی موجود در یک تیر مستطیلی با فاصله y₁ از محور خنثی دارای رابطه درجه دوم است. از این‌رو، با رسم نمودار تغییرات تنش‌های برشی نسبت به ارتفاع مقطع، شکل زیر به دست می‌آید. توجه داشته باشید که تنش برشی در y₁=±h/2 برابر با صفر است.

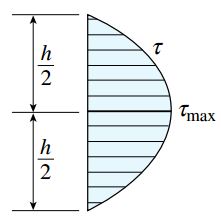
با توجه به نمودار بالا، تنش برشی ماکسیمم در محور خنثی y₁=0 (محلی با بیشترین مقدار گشتاور اول Q) رخ می‌دهد. با جایگذاری y₁=0 در رابطه τ برای یک تیر مستطیلی، به معادله زیر می‌رسیم:

A=bh، مساحت سطح مقطع تیر را نمایش می‌دهد. از این‌رو، تنش برشی ماکسیمم در یک تیر با سطح مقطع مستطیلی، 50 درصد از تنش برشی میانگین V/A بزرگ‌تر است. توجه داشته باشید که معادلات بالا برای محاسبه تنش‌های برشی عمودی اعمال شده بر مقاطع عرضی یا تنش‌های برشی افقی اعمال شده در میان لایه‌های افقی تیر قابل استفاده هستند.

محدودیت‌های استفاده از رابطه برش

محدودیت‌های استفاده از روابط ارائه شده در این مقاله مشابه محدودیت‌های رابطه خمش هستند. بنابراین، این روابط تنها برای تیرهای ساخته شده از مواد الاستیک خطی با اعوجاج‌های کوچک اعتبار دارند. در تیرهایی با سطح مقطع مستطیلی، دقت رابطه برش به نسبت ارتفاع به عرض سطح مقطع بستگی دارد. رابطه برش برای تیرهای خیلی نازک (ارتفاع h بسیار بزرگ‌تر از عرض b)، به عنوان یک روش بسیار دقیق در نظر گرفته می‌شود. اگرچه، با افزایش عرض b نسبت به ارتفاع h، دقت این رابطه کاهش می‌یابد. به عنوان مثال، در تیرهایی با سطح مقطع مربعی (h=b)، مقدار واقعی تنش برشی ماکسیمم حدود 13 درصد از مقدار به دست آمده توسط رابطه برش بزرگ‌تر است.

استفاده از رابطه برش برای برخی از اشکال سطح مقطع نیز مناسب نیست. به عنوان مثال، استفاده از این رابطه برای مقاطع مثلثی و نیم دایره‌ای کاربرد ندارد. برای جلوگیری از به کارگیری نامناسب این رابطه، فرضیات زیر را در نظر داشته باشید:

• الف) اضلاع سطح مقطع باید با محور y موازی باشند تا تنش‌های برشی در راستای موازی با این محور اعمال شوند.
• ب) تنش‌های برشی موجود بر روی عرض سطح مقطع باید به صورت یکنواخت توزیع شده باشند.

فرضیات بالا تنها برای حالت‌های خاص (سطح مقطع دایره‌ای و جانِ تیرهای بال پهن) برقرار هستند.

در انتهای به خاطر داشته باشید که رابطه برش تنها برای تیرهای منشوری (سطح مقطع یکنواخت در راستای محور طولی) کاربرد دارند. اگر تیر مورد بررسی غیرمنشوری باشد (تیرهای مخروطی و ...)، تنش‌های برشی واقعی نسبت به تنش‌های به دست آمده توسط رابطه برش متفاوت خواهند بود.

کرنش برشی

از آنجایی که تنش برشی τ نسبت به ارتفاع یک تیر با مقطع مستطیلی به صورت درجه دو (سهمی‌وار) تغییر می‌کند، رابطه کرنش برشی (γ=τ/G) نیز به صورت درجه دو تغییر خواهد کرد. در اثر ایجاد این کرنش‌های برشی، مقطع تیر که پیش از این به صورت سطح صاف بود؛ به صورت پیچیده درمی‌آید. شکل زیر این پیچش را نمایش می‌دهد. در شکل زیر، مقطع mn و pq در ابتدا دارای سطح صاف بودند.

پس از اعمال تنش این مقاطع به سطوح دارای انحنای m₁n₁ و p₁q₁ تبدیل شدند. کرنش برشی ماکسیمم در این حالت نیز بر روی سطح خنثی رخ می‌دهد. در نقطه p₁ ،m₁ ،n₁ و q₁، مقدار کرنش برشی برابر با صفر است. از این‌رو، منحنی‌های m₁n₁ و p₁q₁ بر سطوح بالایی و پایینی تیر عمود هستند.

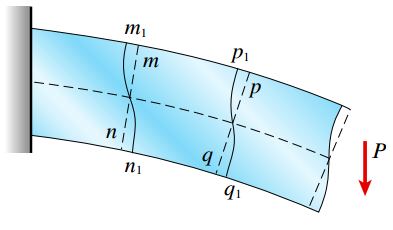
اگر مقدار نیروی برشی V بر روی محور تیر ثابت باشد، پیچش در تمام مقاطع مشابه یکدیگر خواهد بود. از این‌رو، کرنش‌های برشی هیچ تأثیری بر روی افزایش و کاهش طول ناشی از اعمال گشتاورهای خمشی نخواهند داشت. به علاوه، توزیع تنش‌های نرمال، مشابه حالت خمش خالص خواهد بود. مطالعات دقیق صورت گرفته توسط روش‌های پیشرفته تحلیلی نشان می‌دهد که حتی در هنگام تغییر پیوسته نیروی برشی در راستای طول تیر، پیچش ناشی از کرنش‌های برشی تأثیر قابل ملاحظه‌ای بر روی کرنش‌های طولی ندارند. بنابراین، اگرچه رابطه خمش با فرض حالت بارگذاری خمش خالص به دست می‌آید، در اکثر مواقع استفاده از این رابطه برای حالت بارگذاری خمش غیر یکنواخت نیز قابل توجیه است.

مثال‌های کاربردی

در این بخش، به منظور آشنایی بیشتر با روابط ارائه شده در این مقاله و نحوه به کارگیری آن‌ها برای طراحی تیرهای مستطیلی (فلزی و چوبی)، به تشریح دو مثال کاربردی خواهیم پرداخت.

مثال 1

شکل زیر، یک تیر فلزی با مقطع مستطیلی را نشان می‌دهد که در نقاط A و B به صورت ساده نگهداری می‌شود. بار یکنواخت اعمال شده بر روی این تیر (به همراه وزن خود آن) برابر q=160lb/in است. اگر طول تیر L=3ft، عرض آن b=1in و ارتفاع آن h=4in باشد، مقدار تنش نرمال σ_C و تنش برشی τ_C در نقطه C (در فاصله 1 اینچی از بالای تیر و در فاصله 8 اینچی از تکیه‌گاه راست) چقدر خواهد بود؟ (تنش‌های خواسته شده را بر روی یک المان تنش رسم کنید.)

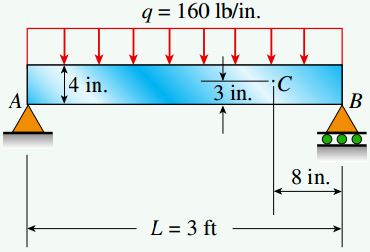
گشتاور خمشی و نیروی برشی

نیروی برشی V_C و گشتاور خمشی M_C در نقطه C بر روی مقطع عرضی تیر برابرند با:

برای آشنایی با نحوه محاسبه این کمیت‌ها و قواعد علامت‌گذاری آن‌ها به مباحث «گشتاور خمشی و نیروی برشی در تیرها» و «مثال‌های طبقه‌بندی شده رسم نمودارهای گشتاور خمشی و نیروی برشی» مراجعه کنید.

ممان اینرسی

ممان اینرسی سطح مقطع تیر حول محور خنثی برابر است با:

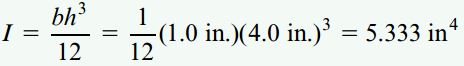
تنش نرمال در نقطه C

تنش نرمال در نقطه C را می‌توان با استفاده از رابطه خمش برای فاصله 1 اینچی از محور خنثی به دست آورد:

علامت منفی در محاسبه بالا بیانگر فشاری بودن تنش است.

تنش برشی در نقطه C

برای تعیین تنش برشی در نقطه C باید در ابتدا گشتاور اول Q_C سطح مقطع بالای این نقطه را محاسبه کنیم. این گشتاور اول با حاصل‌ضرب مساحت ناحیه مذکور در فاصله مرکز هندسی آن (y_C) تا محور z برابر است.

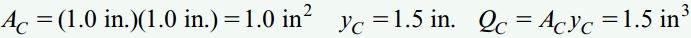
اکنون با جایگذاری مقادیر عددی به دست آمده در رابطه برش، مقدار تنش برشی را نیز به دست می‌آوریم:

با بررسی پیکربندی مسئله می‌توان جهت اعمال این تنش را تعیین کرد؛ چراکه تنش برشی با نیروی برشی اعمال شده هم‌جهت است. در این مثال، نیروی برشی بر روی بخش سمت چپ نقطه C، رو به بالا و بر روی بخش سمت راست نقطه C، رو به پایین اعمال می‌شود. بهترین راه برای نمایش جهات تنش‌های نرمال و برشی، رسم المان تنش است.

المان تنش در نقطه C

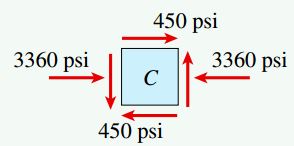
شکل زیر، المان تنش جدا شده از نقطه C را نمایش می‌دهد. تنش‌های فشاری σ_C=3360psi بر روی مقاطع عرضی المان و تنش‌های برشی τ=450psi بر روی سطوح بالایی و پایینی مقاطع اعمال می‌شوند.

مثال 2

در شکل زیر، یک تیر چوبی با سطح مقطع مستطیلی (عرض b=100mm و طول h=150mm) تحت دو بار متمرکز قرار گرفته است. فاصله هر انتهای تیر تا نزدیک‌ترین بارگذاری a=0.5m است. با توجه به اطلاعات مسئله و پیکربندی تیر، حداکثر مقدار مجاز بار P_max را با در نظر گرفتن تنش مجاز فشاری و کششی σ_allow=11MPa به دست بیاورید. تنش برشی مجاز در راستای افقی برابر τ_allow=1.2MPa است (از وزن تیر صرف‌نظر شود).

توجه: مقاومت برشی تیرهای چوبی در راستای افقی (برش موازی با امتداد الیاف چوب) بسیار پایین‌تر از مقاومت برشی آن در جهات دیگر (برش بر روی مقاطع عرضی) است. به همین دلیل در طراحی تیرهای چوبی معمولاً تنش مجاز برای برش افقی در نظر گرفته می‌شود.

نیروی برشی حداکثر در محل قرارگیری تکیه‌گاه‌های تیر و حداکثر گشتاور خمشی در ناحیه بین آن‌ها رخ می‌دهد. برای این مقادیر داریم:

علاوه بر این، مدول مقطع S و مساحت سطح مقطع A برابرند با:

مقدار حداکثری تنش‌های نرمال و برشی موجود در تیر با استفاده از روابط خمش و برش به دست می‌آیند:

به این ترتیب، حداکثر مقادیر مجاز بار P در حالت خمش و برش برابرند با:

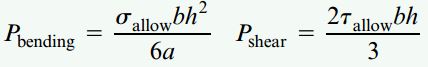
با جایگذاری مقادیر عددی در روابط بالا خواهیم داشت:

با توجه به نتایج به دست آمده، طراحی ما باید از مقدار مجاز تنش خمشی پیروی کند. به این ترتیب، حداکثر بار مجاز برابر است با:

توجه: با در نظر گرفتن وزن تیر در محاسبات می‌توان تحلیل کامل و دقیق‌تری را انجام داد. در این حالت، مقدار بار مجاز کاهش می‌یابد. در ادامه، برخی از نکات کلی قابل توجه در حل مثال‌های مشابه آورده شده است:

• الف) در مثال حاضر، تنش‌های نرمال ماکسیمم و تنش‌های برشی ماکسیمم در یک محل رخ نمی‌دهند. تنش نرمال در میانه تیر (بالا و پایین سطح مقطع) و تنش برشی در نزدیکی تکیه‌گاه‌ها (محور خنثی) دارای مقدار ماکسیمم هستند.
• ب) در اکثر تیرها، تنش‌های خمشی مقدار بار مجاز را کنترل می‌کنند.
• ج) چوب یک ماده همگن نیست و اغلب رفتار الاستیک خطی ندارد. با این وجود می‌توان از روابط خمش و برش برای به دست آوردن نتایج تقریبی استفاده کرد. این نتایج تقریبی معمولاً برای طراحی تیرهای چوبی کافی هستند.

^^