نیروی برشی و گشتاور خمشی در تیرها – به زبان ساده
در مباحث «انواع تیر»، «انواع تکیهگاه»، «انواع عکسالعملهای تکیهگاهی»، «انواع بار»، «انواع رهاساز»، «تعیین عکس العملهای تکیهگاهی تیرها» و «خط تاثیر در تحلیل سازه»، با تعاریف اولیه مرتبط با تیرها و مبانی تحلیل این عضوهای سازهای در شرایط بارگذاری مختلف آشنا شدیم. در این مقاله، به معرفی نیروی برشی و گشتاور خمشی درون تیرها، قواعد علامتگذاری و نحوه تحلیل آنها خواهیم پرداخت. در انتها نیز به منظور آشنایی بیشتر با مطالب ارائه شده، چند مثال را تشریح خواهیم کرد.


نیروی برشی و گشتاور خمشی
اعمال نیرو یا کوپل بر روی یک تیر باعث ایجاد تنش و کرنش در بخشهای داخلی آن میشود. به منظور تعیین این تنشها و کرنشها، در ابتدا باید نیروها و کوپلهای داخلی اعمال شده بر روی مقاطع تیر را به دست بیاوریم. برای آشنایی با نحوه تعیین این کمیتهای داخلی، شکل زیر را در نظر بگیرد. این شکل، تیر یکسر گیردار AB را نمایش میدهد که انتهای آزاد آن در معرض نیروی متمرکز P قرار گرفته است.
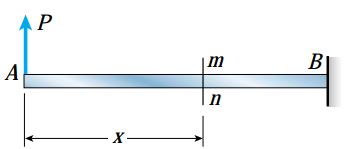
با ایجاد یک برش در فاصله x از انتهای آزاد تیر (مقطع عرضی mn در شکل بالا) میتوانیم نمودارهای جسم آزاد دو بخش ایجاد شده را رسم کنیم. به دلیل وجود نیروی P و تنشهای اعمال شده بر روی مقطع عرضی mn، نمودارهای جسم آزاد در حالت تعادل قرار خواهند داشت.
تنشهای مذکور، تعامل بین بخش سمت چپ و راست تیر را نمایش میدهند. در این مرحله از تحلیل، نحوه توزیع تنشهای اعمال شده بر روی mn مشخص نیست. با این وجود، میدانیم برآیند این تنشها باید به گونهای باشد که جسم آزاد در حالت تعادل باقی بماند.
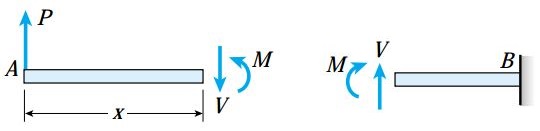
با استفاده از قواعد استاتیک میتوانیم برآیند تنشهای اعمال شده بر روی مقطع عرضی را به یک تنش برشی (V) و یک گشتاور خمشی (M) تجزیه کنیم. به دلیل عرضی بودن بار P نسبت به محور تیر، هیچ نیروی محوری (در راستای محور افقی) بر روی سطح مقطع mn وجود نخواهد داشت. نیروی برشی و گشتاور خمشی در صفحه دربرگیرنده تیر (مقطع طولی) قرار دارند. از اینرو، بردار نیروی برشی در این صفحه و بردار گشتاور خمشی عمود بر آن اعمال میشوند.
نیروهای برشی و گشتاورهای خمشی نظیر نیروهای محوری درون میلهها و گشتاورهای پیچشی درون شفتها، برآیند تنشهای توزیع شده بر روی سطح مقطع هستند. به همین دلیل، این کمیتها مجموعاً با عنوان «برآیندهای تنش» (Stress Resultants) شناخته میشوند. برآیندهای تنش در تیرهای معین استاتیکی را میتوان صرفاً با به کارگیری معادلات تعادل محاسبه کرد. به عنوان مثال، تیر یکسر گیردار زیر و نمودار جسم آزاد بخش سمت چپ مقطع mn را در نظر بگیرید.

با جمع نیروهای موجود در راستای عمودی و تعیین گشتاورهای حول سطح مقطع mn، به روابط زیر خواهیم رسید:

x: فاصله از انتهای آزاد تیر تا سطح مقطع مورد نظر
به این ترتیب، فرآیند محاسبه نیروی برشی و گشتاور خمشی موجود در سازه بالا، به سادگی و تنها با استفاده از نمودار جسم آزاد و دو معادله تعادل صورت میگیرد.
قواعد علامتگذاری
در این بخش، به معرفی نحوه تعیین قواعد علامتگذاری نیروهای برشی و گشتاورهای خمشی میپردازیم. بر اساس قواعد مرسوم، اگر جهتهای اعمال نیروهای برشی و گشتاورهای خمشی مطابق شکل زیر باشند، علامت V و M مثبت در نظر گرفته خواهد شد.
توجه داشته باشید که در این مثال، نیروی برشی تمایل به ایجاد دوران ساعتگرد ماده و گشتاور پیچشی تمایل به فشرده کردن بخش بالایی تیر و همچنین کشیدن بخش پایینی آن دارد. به علاوه، در اینجا نیروی برشی به سمت پایین و گشتاور خمشی به صورت پادساعتگرد اعمال میشود.

شکل زیر، عکسالعمل برآیندهای تنش در بخش سمت راست تیر یکسر گیردار را نمایش میدهد. همان طور که مشاهده میکنید، جهتگیری کمیتهای مورد نظر برعکس شکل بالا (نیروی برشی به سمت پایین و گشتاور خمشی به صورت پادساعتگرد) است. با این وجود، نیروی برشی در این حالت نیز تمایل به ایجاد دوران ساعتگرد ماده و گشتاور خمشی نیز تمایل به فشرده کردن بخش بالایی تیر و همچنین کشیدن بخش پایینی آن دارد.

باید توجه داشته باشید که در وقع علامت جبری برآیند تنش با استفاده از نحوه تغییر شکل ماده به دست میآید و با جهتگیری آن در فضا رابطه مستقیمی ندارد. در تیرها، یک نیروی برشی مثبت به صورت ساعتگرد و یک نیروی برشی منفی به صورت پادساعتگرد بر روی ماده اعمال میشود. علاوه بر این، یک گشتاور خمشی مثبت، بخش بالایی تیر و یک گشتاور خمشی منفی، بخش پایینی تیر را تحت فشار قرار میدهد.
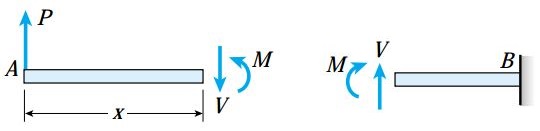
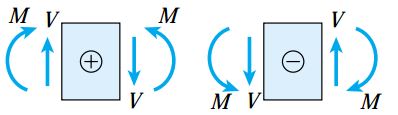
شکل زیر، نیروهای برشی و گشتاورهای خمشی مثبت و منفی را نمایش میدهد. این نیروها و گشتاورها بر روی المان کوچکی از تیر اعمال میشوند.
تغییر شکل یک المان تحت نیروهای برشی و گشتاورهای خمشی مثبت و منفی نیز در شکل زیر نمایش داده شده است. با توجه به این شکل، نیروی برشی مثبت تمایل دارد که صفحه سمت راست المان را نسبت به صفحه سمت چپ آن رو به پایین حرکت دهد. به علاوه، گشتاور خمشی مثبت نیز بخش بالایی المان را تحت فشار و بخش پایینی آن را تحت کشش قرار میدهد.
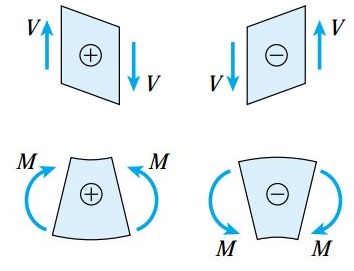
به قواعد علامتگذاری برآیندهای تنش، قواعد علامتگذاری تغییر شکل نیز میگویند؛ چراکه این قواعد بر اساس نحوه تغییر شکل ماده بیان میشوند. به عنوان مثال، با توجه به مطالب ارائه شده در مبحث «تغییر طول عضوهای تحت بار محوری»، در صورت افزایش طول میله بر اثر اعمال نیروی محوری، علامت نیرو مثبت و در صورت کاهش طول آن، علامت نیرو منفی خواهد بود. بنابراین، علامت نیروی محوری به نحوه تغییر شکل ماده بستگی دارد و جهتگیری نیرو تأثیری در تغییر علامت نخواهد داشت.
علامتگذاری در معادلات تعادل
برای نوشتن معادلات تعادل، قواعد علامتگذاری استاتیک مورد استفاده قرار میگیرند. در این قواعد، مثبت یا منفی بودن علامت نیرو به جهتگیری آن در دستگاه محورهای مختصات بستگی دارد. به عنوان مثال، اگر نیروهای موجود در راستای محور y را با هم جمع کنیم، نیروهای اعمال شده در جهت مثبت این محور دارای علامت مثبت و نیروهای اعمال شده در جهت منفی محور دارای علامت منفی خواهند بود. برای درک بهتر این قواعد، شکل زیر را در نظر بگیرید.

این شکل، نمودار جسم آزاد بخش سمت چپ تیر یکسر گیردار را نمایش میدهد. میخواهیم نیروهای موجود در راستای عمودی را با هم جمع کنیم. بخش بالایی محور y را مثبت در نظر میگیریم. به این ترتیب، علامت بار P در معادله تعادل مثبت خواهد بود؛ چراکه این بار در جهت رو به بالای محور y اعمال میشود. با وجود اینکه نیروی برشی V در حالت کلی یک نیروی برشی مثبت به حساب میآید، علامت آن در معادله تعادل منفی در نظر گرفته میشود (جهت رو به پایین). این مثال، تفاوت بین قواعد مورد استفاده برای نیروی برشی (قاعده علامتگذاری تغییر شکل) و قواعد مورد استفاده در معادله تعادل (قاعده علامتگذاری استاتیک) را به خوبی نمایش میدهد.
مثالها
در این بخش، به منظور آشنایی با روشهای مورد استفاده برای تحلیل سازههای تحت نیروی برشی و گشتاور خمشی، به تشریح سه مثال در شرایط بارگذاری مختلف میپردازیم. هدف اصلی از ارائه این مثالها، یادگیری نحوه به کارگیری قواعد علامتگذاری، رسم نمودارهای جسم آزاد و حل معادلات تعادل در مسائل متنوع است.
مثال 1
تیر ساده نمایش داده شده در شکل زیر را در نظر بگیرید. این تیر در معرض دو بار (نیروی P و کوپل M0) قرار دارد. با توجه به پیکربندی تیر AB، نیروی برشی V و گشتاور خمشی M در نقاط زیر را تعیین کنید:
- الف) نقطهای با فاصله کم از بخش سمت چپ مرکز تیر
- ب) نقطهای فاصله کم از بخش سمت راست مرکز تیر

به منظور شروع تحلیل باید در ابتدا نمودار جسم آزاد کل تیر را مطابق شکل زیر رسم کنیم. به دلیل وجود بارگذاری عمودی، مؤلفه افقی عکسالعمل برابر با صفر در نظر گرفته میشود.

اگر مقطعی را دقیقاً در سمت چپ محل اعمال گشتاور M0 و مقطع دیگری را دقیقاً در سمت راست محل اعمال این گشتاور ایجاد کنیم، نمودارهای جسم آزاد زیر به دست میآیند.
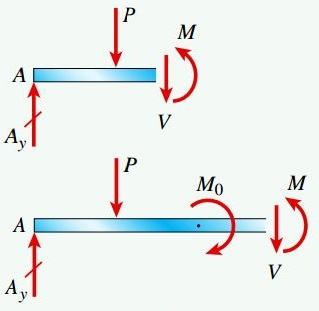
تیر مورد بررسی در این مثال، یک سازه معین استاتیکی است. به منظور دستیابی به رابطه مورد نیاز برای تعیین نیروی عکسالعمل Ay با توجه به کمیتهای P و M0، باید گشتاورهای اعمال شده حول نقطه B را با هم جمع کنیم. برای تعیین نیروی برشی V و گشتاور خمشی M در نقاط مورد نظر نیز میتوانیم نمودارهای جسم آزاد بالا را مورد استفاده قرار دهیم.
نیروی عکسالعمل Ay
در این مرحله از جمع گشتاورهای حول نقطه B و قاعده علامتگذاری استاتیک برای یافتن نیروی عکسالعمل Ay استفاده میکنیم:
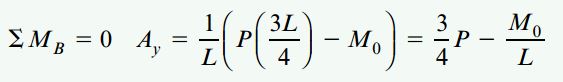
تنها مؤلفه مورد نیاز در تحلیل نمودار جسم آزاد بخش سمت چپ تیر، نیروی Ay است. در صورت تحلیل نمودار جسم آزاد بخش سمت راست، نیروی عکسالعمل B باید مورد محاسبه قرار گیرد:

نیروی برشی و گشتاور خمشی در نزدیکی سمت چپ میانه تیر
در این بخش از نمودار جسم آزاد زیر برای تعیین مؤلفههای مورد نیاز استفاده میکنیم. جهتگیری نیروی برشی V و گشتاور M موجود در شکل زیر مثبت در نظر گرفته میشود.
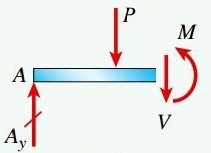
با جمع نیروها و گشتاورهای موجود در سطح مقطع ایجاد شده، روابط مورد نیاز برای تعیین V و M به دست میآیند:
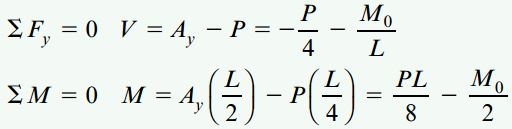
با توجه به روابط به دست آمده، علامت نیروی برشی V منفی است. از اینرو، جهت این نیرو به سمت بالا خواهد بود (برعکس جهت فرضی در نمودار جسم آزاد). گشتاور خمشی M میتواند مثبت یا منفی باشد. علامت این گشتاور به مقادیر نسبی بارهای P و M0 بستگی دارد.
نیروی برشی گشتاور خمشی در نزدیکی سمت راست میانه تیر
تحلیل صورت گرفته در مرحله قبل را برای نمودار جسم آزاد زیر نیز تکرار می کنیم.

در این نمودار جسم آزاد، علاوه بر مولفه های موجود در نمودار قبلی، گشتاور M0 نیز اعمال می شود. به این ترتیب داریم:
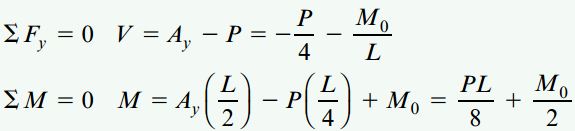
نتایج به دست آمده نشان میدهند که با تغییر مکان سطح مقطع از سمت چپ کوپل M0 به سمت راست آن، نیروی برشی تغییری نمیکند اما گشتاور خمشی به صورت جبری و به اندازه M0 افزایش مییابد (نتایج بخش الف و ب را با هم مقایسه کنید). در صورت استفاده از نمودار جسم آزاد بخش سمت راست تیر نیز نتایج تحلیل مشابه نتایج به دست آمده خواهند بود.
مثال 2
شکل زیر، یک تیر ساده با انتهای آزاد را نمایش میدهد. این تیر در معرض یک بار گسترده یکنواخت با شدت q=400lb/ft قرار دارد که بر روی تمام طول آن اعمال میشود. به علاوه، بار متمرکز P=2400lb نیز در فاصله 9 فوتی از انتهای سمت چپ تیر وجود دارد. فاصله بین دو تکیهگاه A و B برابر با 24 فوت و فاصله بخش آزاد برابر با 6 فوت است. با توجه به پیکربندی تیر و اطلاعات مسئله، مقدار نیروی برشی V و گشتاور خمشی M بر روی سطح مقطعی در نقطه D (فاصله 15 فوتی از A) را محاسبه کنید.

برای شروع تحلیل این مسئله در ابتدا باید عکسالعملهای خارجی و سپس نیروی برشی و گشتاور خمشی داخلی در نقطه D را به دست بیاوریم.
به منظور تعیین نیروهای عکسالعمل RA و RB، از نمودار جسم آزاد کلی تیر (شکل زیر) استفاده میکنیم. به دلیل عمودی بودن هر دو بار اعمال شده، مؤلفه افقی عکسالعمل در تکیهگاه لولایی A صفر خواهد بود.

با ایجاد یک برش در نقطه D، نیروی برشی VD و گشتاور خمشی MD در نقطه D را از طریق نمودارهای جسم آزاد به دست آمده مورد محاسبه قرار میدهیم (شکل زیر). به این منظور میتوانیم از نمودار سمت چپ یا سمت راست استفاده کنیم. بر اساس قاعده علامتگذاری تغییر شکل، نمودارهای جسم آزاد زیر نیروی برشی VD و گشتاور خمشی MD در جهت فرضی مثبت را نمایش میدهند.
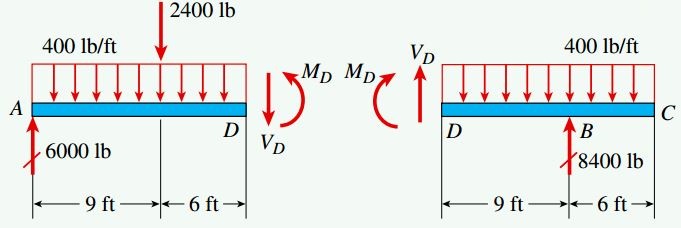
عکسالعملهای خارجی
به منظور تعیین نیروهای عکسالعمل خارجی، نیروهای موجود در راستای y و گشتاورهای حول نقطه A را با در نظر داشتن قاعده علامتگذاری استاتیک با هم جمع میکنیم:
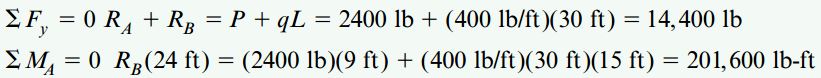
در معادله اول، به جای بار گسترده (q(x، از برآیند آن (qL) در فاصله x=(24+6)/2=15ft (مرکز تیر) استفاده شده است. با حل معادلات بالا، RB=8400lb و RA=6000lb خواهد بود. این مقادیر در نمودار جسم آزاد نیز نمایش داده شدهاند.
نیروی V و گشتاور M در نقطه D
نمودار جسم آزاد سمت چپ نقطه D را در نظر بگیرید:

به جای به کارگیری نمودار جسم آزاد سمت چپ میتوانیم از نمودار سمت راست نیز برای تعیین نیروی برشی VD و گشتاور خمشی MD استفاده کنیم. به این منظور، با جمع نیروهای موجود در راستای عمودی داریم:
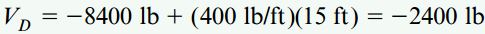
با جمع گشتاورهای حول نقطه D نیز به مقدار زیر میرسیم:

همان طور که مشاهده میکنید این مقادیر با مقادیر به دست آمده از روش قبلی یکسان هستند. به همین دلیل، استفاده از نمودار جسم آزاد سمت چپ یا راست تفاوتی در نتایج نهایی نخواهد داشت.
مثال 3
در شکل زیر، یک تیر ساده با طول L نمایش داده شده است. این تیر در معرض یک بار گسترده متغیر با شدت q(x)=xq0/L قرار دارد. با توجه به اطلاعات مسئله، روابط مورد نیاز برای تعیین نیروی برشی (V(x و گشتاور خمشی (M(x در فاصله x از نقطه A را به دست آورید.
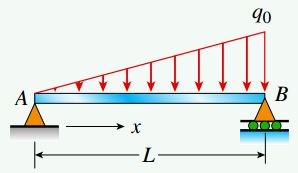
مانند مثالهای قبلی، در اینجا نیز باید در ابتدای تحلیل، عکسالعملهای تکیهگاهی را مشخص کنیم و سپس روابط مورد نیاز برای محاسبه نیروی برشی و گشتاور خمشی را به دست بیاوریم. شکل زیر، نمودار جسم آزاد کل تیر را نمایش میدهد. این نمودار به منظور تعیین نیروهای عکسالعمل RA و RB مورد استفاده قرار میگیرد.
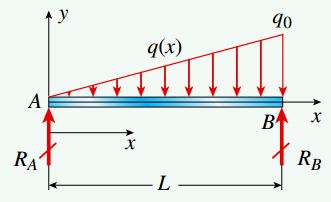
برای نمایش نیروی برشی V و گشتاور خمشی M، برشی را در فاصله x از تکیهگاه A ایجاد میکنیم. این برش، نمودار جسم آزاد کل تیر را به دو نمودار مجزا تقسیم میکند. شکل زیر، نمودار جسم آزاد بخش سمت چپ برش را نمایش میدهد.

بر اساس قاعده علامتگذاری تغییر شکل، جهتگیری نیروی برشی V و گشتاور خمشی M در نمودار بالا مثبت است. در صورت جمع نیروها و گشتاورهای موجود در این مقطع، امکان به دست آوردن توابع (V(x و (M(x فراهم میشود.
عکسالعملهای خارجی
با در نظر گرفتن قاعده علامتگذاری استاتیک و جمع نیروهای موجود در راستای y و گشتاورهای حول نقطه A خواهیم داشت:
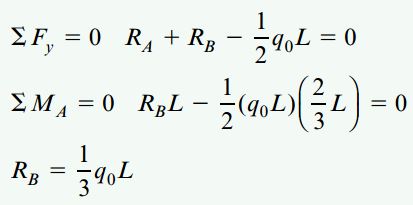
q0L/2: برآیند بار اعمال شده (مساحت مثلث توزیع بار)
اگر RB را در معادله اول قرار دهیم:
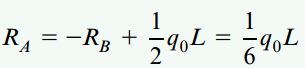
به این ترتیب، عکسالعمل موجود در نقطه A، یک سوم بار کل و عکسالعمل موجود در نقطه B، یک ششم بار کل را تحمل میکند. توجه داشته باشید که عکسالعمل افقی (راستای x) در لولای A برابر با صفر است؛ چراکه هیچ بار افقی یا مؤلفه افقی در بار اعمال شده وجود ندارد.
نیروی داخلی (V(x و گشتاور خمشی (M(x
با جمع نیروها و گشتاورهای موجود در نمودار جسم آزاد سمت چپ، روابط مورد نیاز برای تعیین نیروی داخلی (V(x و گشتاور خمشی (M(x به دست میآید. این روابط، مقدار V و M با توجه به طول تیر را محاسبه میکنند:
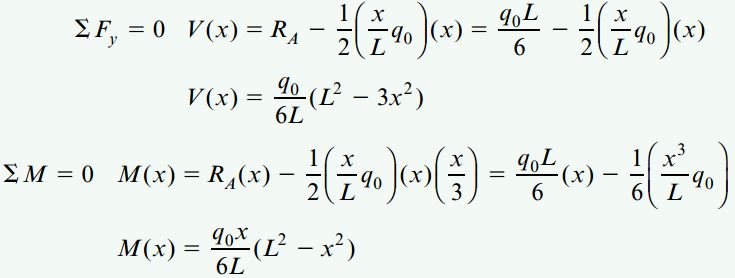
بزرگترین مقدار عددی نیروی برشی در نقطه B قرار دارد. در این محل، RB دو برابر RA است:
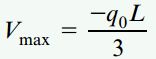
تعیین محل رخ دادن گشتاور ماکسیمم در تیر به سادگی امکانپذیر نیست. به این منظور باید از رابطه (M(x مشتق گرفت و آن را برابر با صفر قرار داد. به این ترتیب، با حل رابطه به دست آمده بر حسب xm، محل اعمال گشتاورهای خمشی مینیمم و ماکسیمم به دست میآید. در نتیجه، با تعیین مقادیر xm و جایگذاری آنها در رابطه (M(x خواهیم داشت:

جواب این معادله برابر است با:
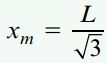
بنابراین:
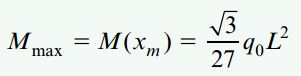
اگر x=0 باشد، V(0)=RA و M(0)=0 خواهد بود (در تکیهگاه A). در صورتی که x=L باشد، V(L)=-RB و M(L)=0 خواهد بود. به دلیل عدم اعمال گشتاور بر روی تکیهگاه غلتکی B، گشتاور موجود در فاصله L نیز برابر با صفر میشود. توجه داشته باشید که رابطه حاصل از مشتق تابع (M(x نسبت به x با تابع (V(x مشابه است. این توابع معمولاً برای رسم نمودار تغییرات نیروی برشی و گشتاور خمشی در طول تیر مورد استفاده قرار میگیرند. این نمودارها کاربردهای زیادی در طراحی تیرها دارند و با به کارگیری آنها میتوان مقادیر و محل وقوع نیروی برشی و گشتاور ماکسیمم را به سادگی تعیین کرد.













سلام علیکم در رابطه ی اخر Mماکزیمم رو چگونه محاسبه کردیدرابطه ی اخر را بیشتر توضیح دهید؟
برای من خیلی مفید بود.ممنون
با سلام و عرض تشکر . در بخش قواعد علامت گذاری ، پاراگراف دوم ، خط دوم : گشتاور خمشی به صورت ساعت گرد درست است.
سلام و روز شما به خیر؛
این مورد در متن مورد بازبینی قرار گرفت اما با توجه به اینکه جمله داخل پرانتز به تصویر بالایی اشاره دارد جهت نیروی برشی باید اصلاح میگردید که این موضوع در مطلب تصحیح و ویرایش شد.
از اینکه با فرادرس همراه هستید، خرسندیم.
با سلام
درمورد تیرهای عمودی و دایروی چطور میشه جهت گشتاور و برش را مشخص کرد؟