تنش برشی و کرنش برشی – آموزش جامع
«تنش برشی» (Shear Stress)، مؤلفهای از تنش است که به صورت مماس بر سطح نمونه مورد آزمایش اعمال میشود. در این مقاله به معرفی نحوه عملکرد تنش برشی، کرنش برشی و قانون هوک در مواد تحت برش خواهیم پرداخت. در انتها نیز علاوه بر تشریح چند مثال کاربردی، جدول مقادیر مدول برشی و الاستیسیته برخی از مواد پرکاربرد مهندسی را برای شما ارائه خواهیم کرد.


تنش برشی در اتصالات پیچی
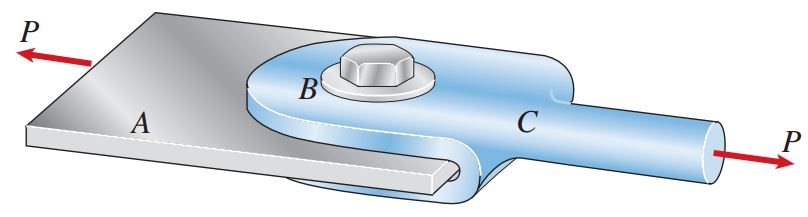
برای درک بهتر نحوه عملکرد تنشهای برشی، اتصال پیچی نمایش داده شده در شکل زیر را در نظر بگیرید. این اتصال شامل یک میله تخت (A)، یک قلاب (C) و یک پیچ (B) است. این پیچ از درون حفرههای میله و قلاب عبور میکند. با اعمال بارهای کششی P، میله و قلاب در خلاف جهت یکدیگر به پیچ فشار وارد میکنند. در این حالت، بر روی سطح تماس پیچ و دو قطعه دیگر تنشی موسوم به «تنش لهیدگی» (Bearing Stress) ایجاد میشود. به این ترتیب، میله و قلاب در راستای ایجاد برش در پیچ و تنشهای برشی در راستای مقابله با ایجاد برش در پیچ عمل میکنند.
برای نمایش بهتر فعل و انفعالات تنشهای برشی درون اتصال پیچی بالا، نمای جانبی آن در شکل زیر آورده شده است. با در نظر گرفتن این نما، نمودار جسم آزاد پیچ را رسم میکنیم. تنشهای لهیدگی اعمال شده توسط قلاب بر روی پیچ در سمت چپ نمودار جسم آزاد و با شمارههای 1 و 3 مشخص شدهاند. تنشهای اعمال شده توسط میله بر روی پیچ در سمت راست و با شماره 2 به نمایش درآمدهاند.
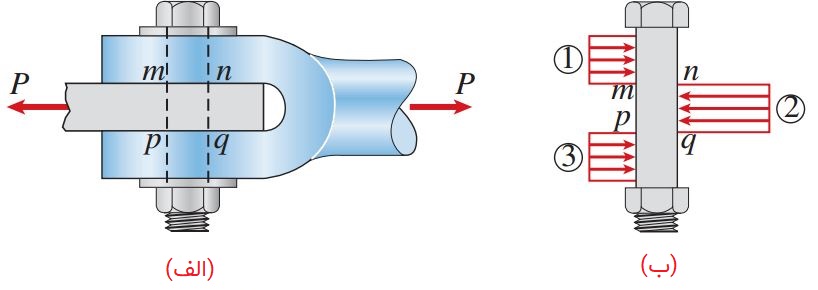
تعیین توزیع واقعی تنشهای لهیدگی دشوار است. بنابراین، معمولاً فرض میشود که این تنشها به صورت یکنواخت توزیع شدهاند. بر اساس فرض یکنواخت بودن توزیع تنشها، میانگین تنش لهیدگی σb با استفاده از رابطه زیر محاسبه میشود:
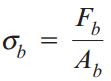
σb: تنش لهیدگی میانگین؛ Fb: نیروی لهیدگی کل؛ Ab: مساحت لهیدگی
برای آشنایی با نحوه تعیین مساحت لهیدگی، تنش لهیدگی توزیع شماره 1 را در نظر بگیرید. Ab برای این تنشها، مساحت مستطیلی به طولِ ضخامت قلاب و عرضِ قطر پیچ است. مقدار Fb نیز از رابطه P/2 به دست میآید. مساحت و نیروی لهیدگی برای تنشهای شماره 3 نیز با همین روش تعیین میشوند. اکنون تنشهای لهیدگی بین میله تخت و پیچ (تنشهای شماره 2) را در نظر بگیرید. Ab برای این تنشها، مساحت مستطیلی با طول ضخامت میله تخت و عرض قطر پیچ است. مقدار Fb در این مورد با بار P برابری میکند.
بر اساس نمودار جسم آزاد نمایش داده شده در شکل زیر، تمایل به ایجاد برش در امتداد مقطع mn و pq وجود دارد. با در نظر گرفتن بخش mnpq میتوان مشاهده کرد که نیروهای برشی V بر روی سطوح برش پیچ اعمال میشوند. این مثال خاص دارای دو صفحه برش mn و pq است. به همین دلیل، پیچ در معرض «برش مضاعف» (Double Shear) قرار دارد. در برش مضاعف، هر یک از نیروهای برشی با نصف بار اعمال شده بر پیچ برابر است (V=P/2).
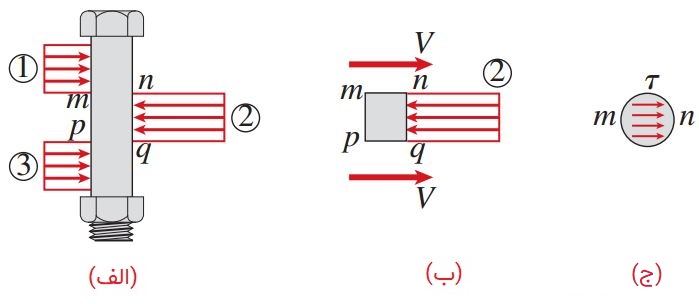
نیروهای برشی V، برآیند تنشهای برشی توزیع شده بر روی سطح مقطع پیچ هستند. به عنوان مثال، تنشهای برشی اعمال شده بر روی مقطع mn در شکل بالا را در نظر بگیرید. این تنشها به موازات سطح برش اعمال میشوند. نحوه توزیع این تنشها به طور دقیق مشخص نیست اما مقدار آنها در مرکز به حداکثر و در لبهها به صفر میرسد. تنشهای برشی معمولاً با حرف یونانی تاو (?) نمایش داده میشود.
در شکل زیر، یک اتصال پیچی تحت «برش منفرد» (Single Shear) نمایش داده شده است. در این اتصال، نیروی محوری P در میله فلزی به فلنجِ یک ستون فولادی اعمال میشود. نمای سطح مقطع این ستون، جزئیات بیشتری از نحوه پیکربندی این اتصال پیچی را نمایش میدهد. در کنار این نما، تصویر توزیع فرضی تنشهای لهیدگی اعمال شده بر روی پیچ قرار دارد. همانگونه که قبلاً نیز اشاره شد، توزیع واقعی تنشهای لهیدگی بسیار پیچیدهتر از توزیع فرضی آنها است. علاوه بر این، تنشهای لهیدگی در مقابل سطوح داخلی سرپیچ و مهره نیز گسترش مییابند. از اینرو، شکل ج نمودار جسم آزاد این اتصال پیچی نیست بلکه تنها تنشهای لهیدگی اعمال شده بر تنه پیچ را نمایش میدهد.
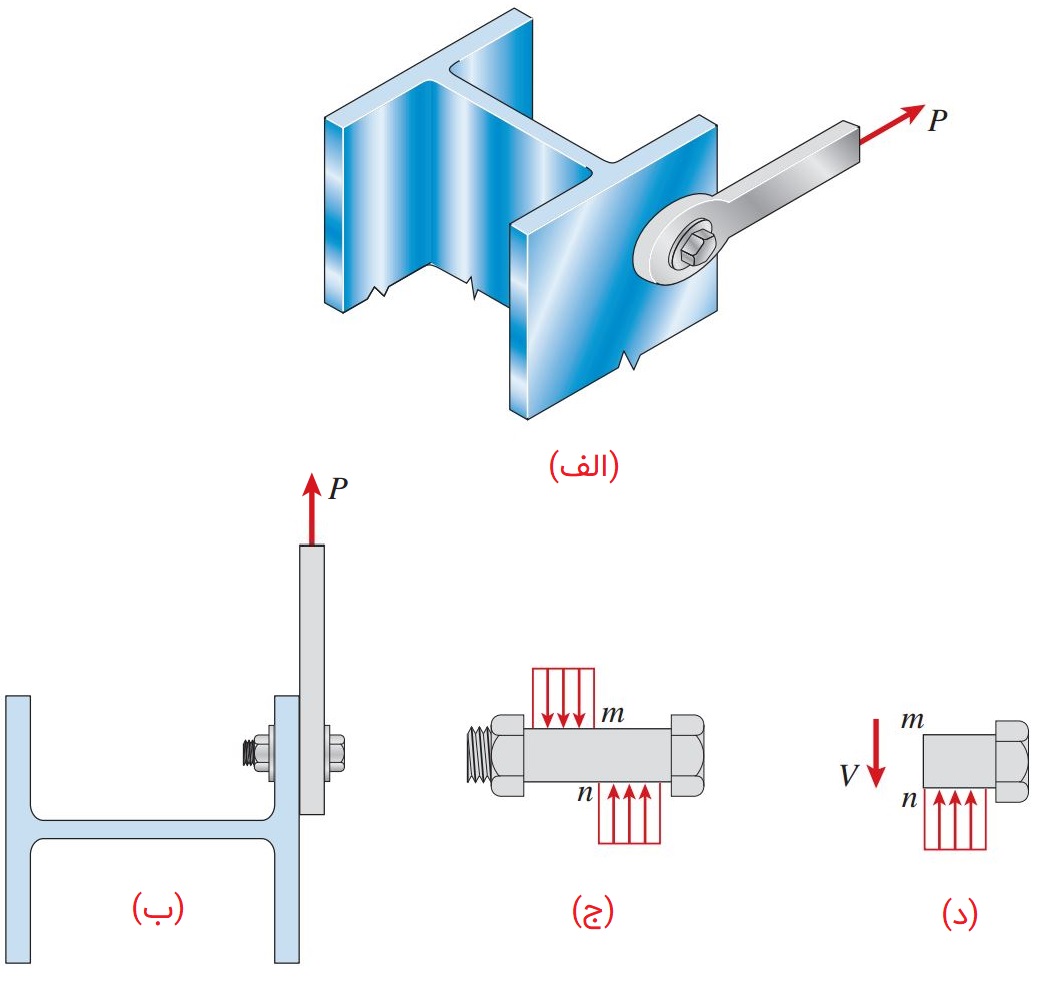
با ایجاد یک برش در مقطع mn، نمودار جسم آزاد پیچ به دست میآید (شکل د). این نمودار نیروی برشی V (برابر با بار P) اعمال شده بر روی سطح مقطع پیچ را نمایش میدهد. این نیروی برشی برآیند تنشهای برشی اعمال شده بر روی سطح مقطع پیچ است. در شکل زیر میتوانید نمونهای از تغییر شکل یک پیچ تحت بارگذاری برش منفرد در لحظه رخ دادن شکست را مشاهده کنید.

در مطالب ارائه شده راجع به اتصالات پیچی، اصطکاک بین قطعات متصل به هم نادیده گرفته شد. وجود اصطکاک بین قطعات بیانگر مقاومت نیروهای اصطکاکی در برابر بارهای اعمال شده بر روی آن قطعات و در نتیجه کاهش میزان بارهای اعمال شده بر روی پیچها است. به دلیل غیر قابل اتکا بودن نیروهای اصطکاکی و دشوار بودن تخمین آنها، معمولاً از در نظر گرفتن این نیروها در محاسبات صرف نظر میشود.
تنش برشی میانگین بر روی سطح مقطع یک پیچ از طریق رابطه زیر به دست میآید:
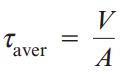
V: نیروی برشی کل؛ A: مساحت سطح مقطع
در یک پیچ تحت برش منفرد، نیروی برشی V برابر با بار P و مساحت A برابر با مساحت سطح مقطع پیچ است. اگرچه، در یک پیچ تحت برش مضاعف، نیروی V برابر با P/2 خواهد بود.
بارگذاریهای نمایش داده شده در شکلهای بالا، نمونههایی از «برش مستقیم» (Direct Shear) یا «برش ساده» (Simple) هستند. در این حالت، تنشهای برشی توسط اعمال مستقیم نیرو بر روی ماده ایجاد میشوند. برش مستقیم در طراحی پیچها، میخها، پرچها، کلیدها، جوشها و مفاصل چسبی رخ میدهد. آشنایی با تنش برشی و دیگر انواع تنش، برای یادگیری مقاومت مصالح و حل مسائل مرتبط با آن ضروری است. از اینرو، مجله فرادرس، مطلبی با عنوان «مقاومت مصالح چیست؟ – پارامترها و مفاهیم پایه به زبان ساده» را تهیه کرده است که ضمن معرفی تنش و کرنش برشی، به مرور مهمترین پارامترها و مفاهیم مقاومت مصالح میپردازد.
واحد تنش برشی
در معادله تنش برشی میانگین مشاهده کردیم که این نوع تنش همانند تنش نرمال، شدت نیرو یا مقدار نیرو در واحد سطح را نمایش میدهد. از اینرو، تنش برشی نیز همانند تنش نرمال در سیستم بریتانیایی با واحد پوند بر اینچ مربع (psi) یا کیلو پوند بر اینچ مربع (ksi) و در سیستم SI با واحد پاسکال (Pa) یا مضربی از پاسکال بیان میشود.
برابری تنشهای برشی بر روی صفحات عمود
برای درک کامل نحوه فعل و انفعالات تنشهای برشی، المان کوچکی از ماده به شکل یک متوازی السطوح قائم را در نظر بگیرید که ابعاد آن در راستای محورهای y ،x و z به ترتیب برابر با b ،a و c است (شکل زیر). هیچ تنشی به صفحات جلویی و پشتی این المان وارد نمیشود. اکنون فرض کنید که تنش برشی ?1 به صورت یکنواخت بر روی صفحه سمت راست با مساحت bc توزیع شده است. به منظور قرارگیری المان در حالت تعادل، نیروی برشی کل اعمال شده بر روی صفحه سمت راست (?1bc) باید توسط یک نیروی برشی هماندازه و با جهت مخالف بر روی صفحه سمت چپ خنثی شود. به دلیل برابر بودن مساحتهای هر دو صفحه، باید تنشهای موجود بر روی آنها نیز با هم برابر باشند.
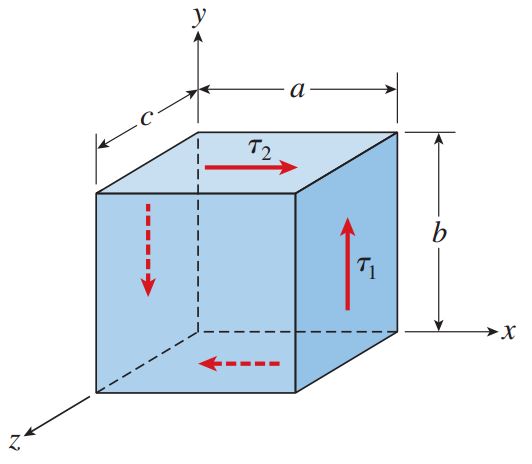
نیروی اعمال شده بر روی صفحه سمت چپ (?1bc) باعث ایجاد یک کوپل به همراه گشتاوری حول محور z با مقدار ?1abc میشود که در شکل بالا به صورت پادساعتگرد عمل میکند. برای قرارگیری المان در حالت تعادل، این گشتاور باید توسط گشتاور حاصل از تنشهای برشی اعمال شده بر روی صفحات بالایی و پایینی المان خنثی شود. تنشهای اعمال شده بر روی صفحه بالایی با ?2 نمایش داده شدهاند. مقدار نیروهای برشی مرتبط با این تنشها برابر ?2ac است. این نیروها نیز گشتاوری معادل ?1abc را به وجود میآورند. با در نظر گرفتن تعادل بین گشتاورهای المان حول محور z مشاهده میکنیم که ?1abc برابر با ?2abc است یا به عبارت دیگر:

به این ترتیب، تمام تنشهای برشی اعمال شده بر المان دارای مقادیر یکسان هستند. به طور خلاصه، با بررسی تنشهای برشی اعمال شده بر روی المانی با وجوه قائم به نتایج زیر دست مییابیم:
- تنشهای اعمال شده بر روی صفحات مقابل یا موازی در یک المان، دارای مقادیر یکسان و جهتگیری مخالف هستند.
- تنشهای اعمال شده بر روی صفحات مجاور یا عمود در یک المان، دارای مقادیر یکسان هستند. جهتگیری این تنشها به گونهای است که یا هر دو به سمت یک نقطه بر روی خط تقاطع صفحات نزدیک میشوند یا هر دو از آن نقطه فاصله میگیرند.
نتایج بالا برای یک المان تحت تنشهای برشی و بدون در نظر گرفتن تنشهای نرمال به دست میآیند (مانند المان زیر). به حالت تنش در این شرایط، «برش خالص» (Pure Shear) گفته میشود.

در اکثر مواقع، نتایج بالا حتی در صورت وجود تنشهای نرمال نیز صادق است؛ چراکه تنشهای نرمال اعمال شده بر روی صفحات موازیِ یک المان کوچک معمولاً مقادیر یکسانی دارند. به همین دلیل، وجود این تنشها بر روی معادلات تعادل مورد استفاده در این بخش تأثیری نخواهند داشت.
کرنش برشی
اعمال تنشهای برشی بر روی یک المان باعث تشکیل کرنشهای برشی میشود. برای درک بهتر نحوه عملکرد کرنشهای برشی، تصویر زیر را در نظر بگیرید. در هنگام تشکیل این نوع کرنش، هیچ تغییر طولی در راستای y ،x یا z رخ نمیدهد. به عبارت دیگر، ابعاد صفحات المان در حین اعمال تنشهای برشی ثابت باقی میماند اما شکل المان تغییر میکند. در این شرایط، المان اولیه از یک متوازی السطوح قائم به یک متوازی السطوح مورب تبدیل میشود. علاوه بر این، صفحات جلویی و پشتی آن نیز به شکل لوزی درمیآیند.
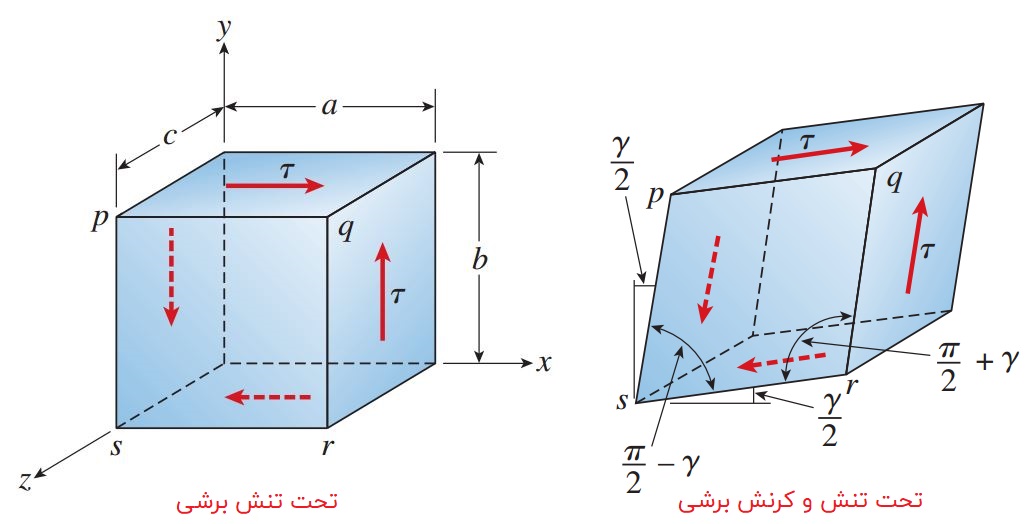
با توجه به تغییر شکلهای به وجود آمده، زوایای بین وجوه المان تغییر میکند. به عنوان مثال، گوشههای q و s در ابتدا دارای زاویه π/2 بودند. پس از ایجاد کرنشهای برشی، زاویه آنها به اندازه γ کاهش یافت (π/2-γ). در عین حال، زوایای p و r به اندازه γ افزایش یافتند (π/2+γ). زاویه γ معیاری برای اندازهگیری میزان «انحراف» (Distortion) یا تغییر شکل المان است. این زاویه با عنوان «کرنش برشی» (Shear Strain) شناخته میشود.
قواعد علامتگذاری تنشها و کرنشهای برشی
به منظور استفاده از قواعد علامتگذاری تنشها و کرنشهای برشی، در ابتدا به یک قاعده کلی برای نامگذاری و تشخیص صفحات مختلف المانهای تنش نیاز داریم. از این پس، صفحات قرار گرفته در راستای مثبت محورهای مختصات را به عنوان صفحات مثبت در نظر میگیریم. به عبارت دیگر، بردار نرمال یک صفحه مثبت با راستای مثبت یکی از محورهای مختصات همجهت است. صفحات منفی نیز در مقابل صفحات مثبت قرار دارند. به این ترتیب، صفحات سمت راست، بالایی و جلویی المان نمایش داده شده در شکل زیر به ترتیب صفحات مثبت y ،x و z و صفحات قرار گرفته در مقابل آنها به ترتیب صفحات منفی y ،x و z خواهند بود.

با در نظر گرفتن اصول نامگذاری در پاراگراف بالا، قواعد علامتگذاری تنشهای برشی به صورت زیر خواهد بود:
- اگر تنش برشی موجود بر روی یک صفحه مثبت در جهت مثبت محورهای مختصات اعمال شود، علامت آن تنش مثبت خواهد بود.
- اگر تنش برشی موجود بر روی یک صفحه مثبت در جهت منفی محورهای مختصات اعمال شود، علامت آن تنش منفی خواهد بود.
- اگر تنش برشی موجود بر روی یک صفحه منفی در جهت منفی محورهای مختصات اعمال شود، علامت آن تنش مثبت خواهد بود.
- اگر تنش برشی موجود بر روی یک صفحه منفی در جهت مثبت محورهای مختصات اعمال شود، علامت آن تنش منفی خواهد بود.
به این ترتیب، علامت تمام تنشهای نمایش داده شده در شکل بالا مثبت است.
قواعد علامتگذاری کرنشهای برشی به صورت زیر بیان میشود:
- اگر زاویه بین دو صفحه مثبت یا دو صفحه منفی کاهش پیدا کند، علامت کرنش برشی مثبت خواهد بود.
- اگر زاویه بین دو صفحه مثبت یا دو صفحه منفی افزایش پیدا کند، علامت کرنش برشی منفی خواهد بود.
بنابراین، علامت کرنشهای نمایش داده شده در شکل بالا مثبت است. به علاوه، همان طور که مشاهده میکنید، تنشهای برشی مثبت به همراه کرنشهای برشی مثبت رخ میدهند.
قانون هوک برای مواد تحت برش
به منظور تعیین خواص مواد تحت برش، معمولاً روشهای تجربی نظیر آزمایش برش مستقیم یا آزمایش پیچش مورد استفاده قرار میگیرند. در آزمایش پیچش، با پیچاندن لولههای مدور توخالی یک حالت برش خالص درون ماده به وجود میآید. با اندازهگیری تغییرات تنش و کرنش برشی موجود در نمونهها، منحنی تنش-کرنش برشی آنها بر اساس نتایج به دست آمده رسم میشود. این منحنی تغییرات تنش برشی ? نسبت به کرنش برشی γ را نمایش میدهد. در مواد یکسان، منحنی تنش-کرنش برشی با منحنی تنش-کرنش کششی (σ در مقابل ε) از نظر مقداری با هم تفاوت دارند اما شکل آنها مشابه یکدیگر است.
منحنی تنش-کرنش برشی برای تعیین خواصی نظیر حد الاستیک، مدول الاستیسیته، تنش تسلیم و تنش نهایی نیز کاربرد دارد. مقادیر به دست آمده برای هر یک از این موارد در حالت برش حدود نصف این مقادیر در حالت کشش است. به عنوان مثال، تنش تسلیم فولاد سازهای تحت کشش بین 0.5 تا 0.6 تنش تسلیم فولاد سازهای تحت کشش است.
بخش اولیه منحنی تنش-کرنش برشی در بسیاری از مواد به صورت یک خط مستقیم است. مقادیر تنش و کرنش برشی در محدوده الاستیک خطی متناسب هستند. بنابراین، قانون هوک برای مواد تحت برش به صورت زیر نوشته میشود:
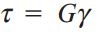
G: مدول برشی الاستیسیته یا مدول صلبیت
مدول برشی (G) نیز همانند مدول الاستیسیته (E)، با واحد مگاپاسکال (MPa) یا گیگاپاسکال (GPa) بیان میشود. معادله زیر، رابطه بین مدول برشی و کششی را نمایش میدهد:
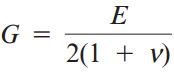
ν: نسبت پواسون
مثالهای کاربردی
در ادامه به منظور آشنایی با تحلیل مسائل مربوط به تنشهای برشی، به تشریح دو مثال کاربردی میپردازیم.
مثال 1
در تصویر زیر، وسیلهای به نام پانچ نمایش داده شده است که برای ایجاد حفره در صفحات فولادی مورد استفاده قرار میگیرد. قطر این پانچ 20 میلیمتر و ضخامت صفحه فولادی 8 میلیمتر است. اگر نیروی مورد نیاز برای ایجاد یک حفره درون صفحه فولادی 110 کیلو نیوتن باشد، مقدار تنش برشی میانگین در صفحه و تنش فشاری میانگین در پانچ چقدر خواهد بود؟
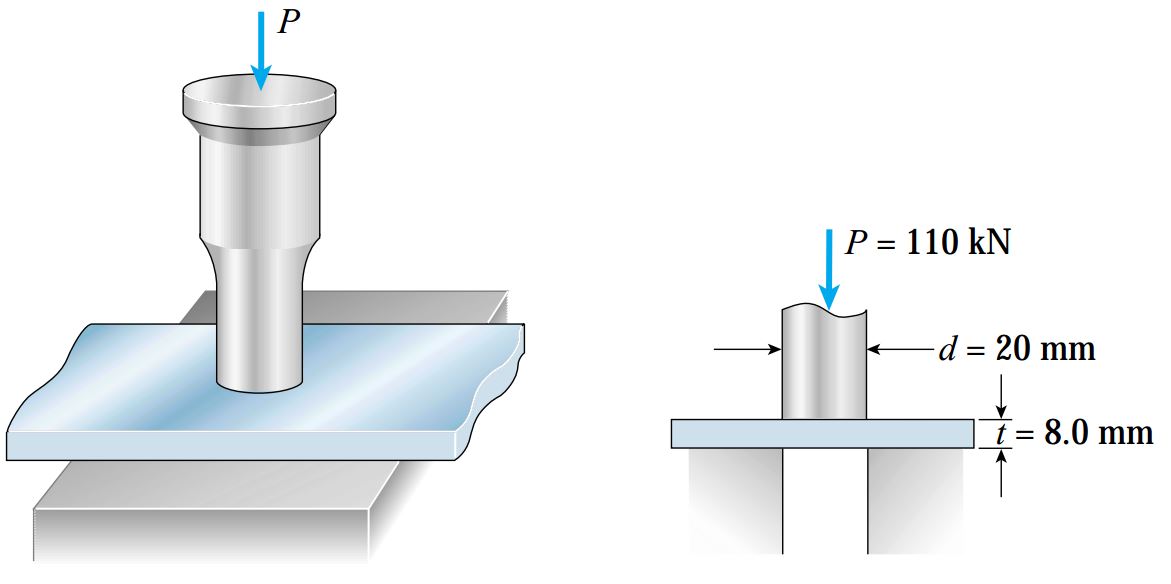
تنش برشی میانگین از تقسیم نیروی P بر مساحت برش صفحه به دست میآید. مساحت برش (As) در این مثال برابر است با حاصلضرب محیط حفره در ضخامت صفحه:
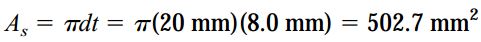
d: قطر پانچ؛ t: ضخامت صفحه
بنابراین، برای محاسبه تنش برشی میانگین داریم:
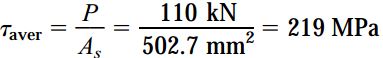
تنش فشاری میانگین نیز به صورت زیر محاسبه میشود:
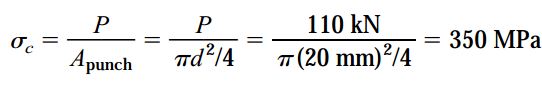
Apunch: مساحت سطح مقطع پانچ
توجه: شرایط این مسئله بسیار ایدئال در نظر گرفته شده است زیرا از اثرات ضربه در هنگام برخورد پانچ به صفحه صرف نظر میشود. در نظر گرفتن این اثرات نیازمند به کارگیری روشهای تحلیل پیشرفته است.
مثال 2
در تصویر زیر، یک ضربهگیر یا اصطلاحاً بالشتک زیرسری نمایش داده شده است. این قطعه برای نگهداری دستگاهها و ستون پلها مورد استفاده قرار میگیرد و از یک ماده الاستیک خطی (معمولاً یک الاستومر نظیر لاستیک) به همراه یک پوشش فولادی تشکیل میشود. فرض کنید که ضخامت الاستومر تشکیلدهنده این بالشتک h، ابعاد صفحه فولادی a*b و نیروی برشی اعمال شده به صفحه V است. با توجه به اطلاعات مسئله، رابطه تعیین تنش برشی میانگین (?aver) در الاستومر و جابجایی افقی صفحه (d) را به دست آورید.
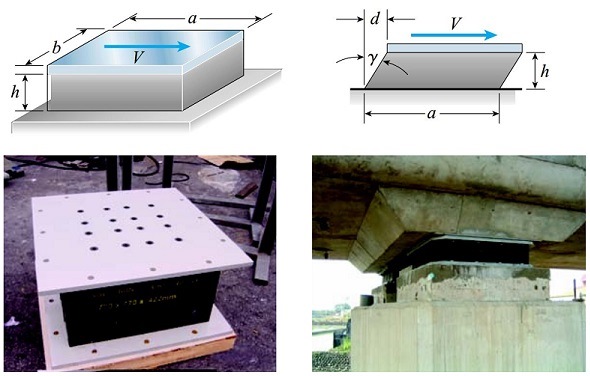
فرض کنید که تنش برشی در سراسر الاستومر به صورت یکنواخت توزیع شده است. به این ترتیب، مقدار تنش برشی بر روی تمام صفحات افقی درون الاستومر از رابطه زیر به دست میآید:

با توجه به قانون هوک در هنگام اعمال برش، رابطه کرنش برشی به صورت زیر نوشته میشود:
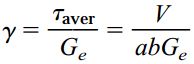
Ge: مدول برشی الاستومر
در نهایت، میزان جابجایی افقی صفحه فولادی برابر با رابطه زیر خواهد بود:

در اکثر مسائل کاربردی، کرنش برشی γ یک زاویه کوچک است. به همین دلیل، با جایگذاری γ به جای tanγ، رابطه بالا به صورت زیر نوشته میشود:
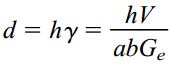
روابط بالا، مقدار تقریبی جابجایی افقی صفحه فولادی را تعیین میکنند زیرا این روابط بر اساس فرض ثابت بودن تنش و کرنش برشی در سراسر الاستومر به دست آمدهاند. در واقعیت، مقدار تنش برشی در گوشههای ماده صفر است. بنابراین، تغییر شکل ماده نسبت به شرایط این مسئله پیچیدهتر خواهد بود. با این وجود، اگر طول صفحه نسبت به ضخامت الاستومتر بزرگ باشد، نتایج به دست آمده از روابط بالا برای مقاصد طراحی کفایت میکنند.
مقادیر مدول برشی و الاستیسیته برای برخی از مواد پرکاربرد مهندسی
جدول زیر، مقادیر مدول برشی برخی از مواد پرکاربرد در مسائل مهندسی را نمایش میدهد.
| ماده | مدول برشی بر حسب GPa |
| آلیاژهای آلومینیوم
2014-T6 6061-T6 7075-T6 | 26-30
28 26 27 |
| برنج | 36-41 |
| برنز | 36-44 |
| آهن ریختهگری | 32-69 |
| مس و آلیاژهای مس | 40-47 |
| شیشه | 19-35 |
| آلیاژهای منیزیوم | 15-17 |
| مونل (70 درصد نیکل و 30 درصد مس) | 66 |
| نیکل | 80 |
| لاستیک | 0.0002-0.001 |
| فولاد | 75-80 |
| آلیاژهای تیتانیوم | 39-44 |
| تنگستن | 140-160 |












