تحلیل میله های تحت پیچش – آموزش جامع

در مبحث «پیچش و تغییر شکل‌های ناشی از آن»، کرنش‌های برشی موجود بر روی سطح و درون یک میله دایره‌ای شکل در شرایط بارگذاری پیچشی را مورد ارزیابی قرار دادیم. در این مقاله، جهت‌گیری و مقدار تنش‌های برشی مربوط به این شرایط را تحلیل خواهیم کرد. در انتها نیز به منظور آشنایی با روابط ارائه شده، به تشریح چند مثال خواهیم پرداخت. در همین راستا برای درک بهتر مبحث «تحلیل میله‌های تحت پیچش» با مجله فرادرس همراه باشید.

مولفه های تنش در میله تحت پیچش

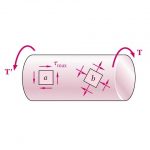
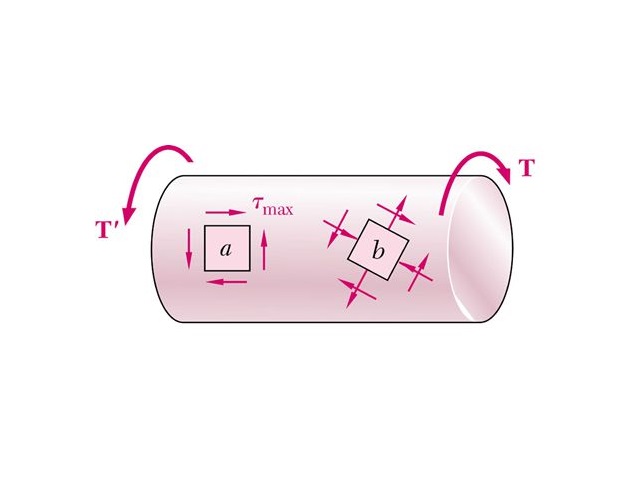
شکل زیر، نحوه تعیین جهت‌گیری تنش‌های ناشی از اعمال بارهای پیچشی را نمایش می‌دهد. با توجه شکل، گشتاور T باعث دوران پادساعت‌گرد انتهای راست میله می‌شود. جهت‌گیری تنش‌های برشی موجود در یک المان تنش بر روی سطح میله مطابق وضعیت نمایش داده شده در این شکل خواهد بود.

همان‌گونه که مشاهده می‌کنید، المان مورد نظر به صورت دوبعدی رسم شده است. این کار تنها برای تسهیل فرآیند تحلیل صورت می‌گیرد. از این‌رو، به خاطر داشته باشید که المان‌های تنش همیشه سه‌بعدی هستند و ضخامت آن‌ها در راستای عمود بر صفحه در نظر گرفته می‌شود.

مقادیر مؤلفه‌های تنش برشی بر روی این المان‌ها با استفاده از مقادیر کرنش‌های ناشی از پیچش و قانون هوک برای مواد تحت برش به دست می‌آیند:

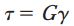
G: مدول برشی؛ γ: کرنش برشی بر حسب رادیان

با ترکیب این معادله و معادلات کرنش‌های برشی در شرایط بارگذاری پیچشی، خواهیم داشت:

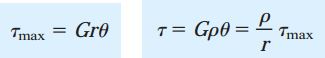
τ_max: تنش برشی در سطح خارجی میله؛ r: شعاع میله؛ θ: نرخ پیچش (رادیان بر واحد طول)؛ τ: تنش برشی در نقطه‌ای درون میله؛ ρ: فاصله شعاعی نقطه مورد بررسی تا مرکز میله

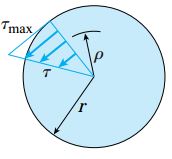
روابط بالا نشان می‌دهند که مقدار تنش‌های برشی نسبت به فاصله شعاعی نقطه مورد بررسی تا مرکز میله به صورت خطی تغییر می‌کند (شکل زیر). این تغییرات خطی تنش، یکی از پیامدهای قانون هوک است. اگر رابطه تنش-کرنش به صورت غیر خطی باشد، تنش‌های برشی نیز به صورت غیر خطی تغییر خواهند کرد. به این ترتیب، برای تحلیل سازه مورد نظر باید روش‌های دیگری را مورد استفاده قرار داد.

تنش‌های برشی اعمال شده بر روی یک مقطع عرضی همراه با تنش‌های برشی هم‌اندازه بر روی مقاطع طولی ایجاد می‌شوند (شکل زیر). این موضوع با برابر بودن تنش‌های برشی بر روی صفحات عمود بر هم مطابقت دارد. اگر مقاومت برشی میله در مقاطع طولی کمتر از مقاومت برشی آن در مقاطع عرضی باشد (مانند چوب)، اولین ترک ناشی از اعمال پیچش، بر روی سطح طولی میله ظاهر خواهد شد.

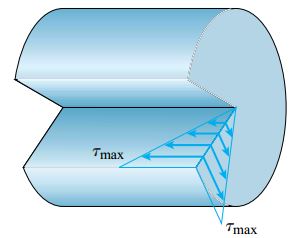
تنش‌های برشی بر روی مقاطع طولی و عرضی در یک میله دایره‌ای شکل (شرایط بارگذاری پیچشی)

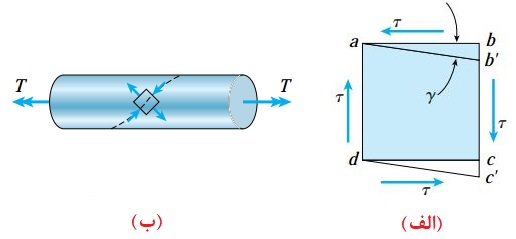
حالت برش خالص بر روی سطح یک میله، معادلِ تنش‌های کششی و فشاری اعمال شده بر روی یک المان دوران یافته تحت زاویه 45 درجه است. بنابراین، یک المان مربعی تحت پیچش که اضلاع آن با محور شفت زاویه 45 درجه می‌سازند، مانند شکل زیر در معرض تنش‌های کششی و فشاری قرار خواهد داشت. اگر یک میله تحت پیچش از ماده‌ای ساخته شده باشد که مقاومت کششی آن کمتر از مقاومت برشی است، شکست در راستای یک خط مارپیچی تحت زاویه 45 درجه نسبت به محور پیچش رخ خواهد داد. این پدیده را می‌توان در هنگام پیچاندن یک تکه گچ مشاهده کرد.

رابطه پیچش

قدم بعدی برای اجرای تحلیل، تعیین رابطه بین تنش‌های برشی و گشتاور پیچشی است. با انجام این کار می‌توانیم تنش و کرنش‌های موجود در یک میله دایره‌ای را محاسبه کنیم.

شکل‌های زیر، توزیع تنش‌های برشی بر روی سطح مقطع یک میله دایره‌ای را نمایش می‌دهند. به دلیل اعمال پیوسته این تنش‌ها در اطراف سطح مقطع، برآیند آن‌ها همانند یک گشتاورِ برابر با گشتاور پیچشی اعمال شده بر میله خواهد بود.

به منظور تعیین برآیند تنش‌های برشی، المان سطح dA در فاصله شعاعی ρ از محور میله را مطابق شکل زیر در نظر می‌گیریم. نیروی برشی اعمال شده بر روی این المان برابر با τdA است. کمیت τ، تنش برشی در فاصله شعاعی ρ را نمایش می‌دهد. گشتاور این نیرو حول محور میله از ضرب نیرو در فاصله شعاعی به دست می‌آید (τρdA).

تعیین برآیند تنش‌های برشی اعمال شده بر روی یک مقطع عرضی

با استفاده از رابطه τ=ρτ_max/r می‌توانیم گشتاور المان مورد بررسی را به صورت زیر بیان کنیم:

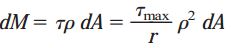
گشتاور پیچشی کل (T)، از جمع گشتاورهای به وجود آمده بر روی تمام المان‌های سطح به دست می‌آید:

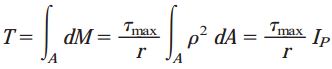
که در آن:

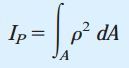
انتگرال بالا، «ممان اینرسی قطبی» (Polar Moment of Inertia) برای سطح مقطع دایره‌ای شکل است. برای دایره‌ای با شعاع r یا قطر d، ممان اینرسی قطبی به صورت زیر محاسبه می‌شود:

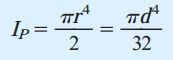
در صورت بازنویسی رابطه گشتاور کل، رابطه‌ای برای تعیین تنش برشی ماکسیمم به دست می‌آید:

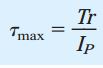
این رابطه با عنوان «رابطه پیچش» (Torsion Formula) شناخته می‌شود. بر اساس رابطه پیچش، تنش برشی ماکسیمم با گشتاور پیچشی اعمال شده رابطه مستقیم و با ممان اینرسی قطبی رابطه عکس دارد. با جایگذاری r=d/2 و I_P=πd⁴/32 در رابطه پیچش، تنش برشی ماکسیمم به صورت زیر تعیین می‌شود:

این رابطه تنها برای میله‌های توپر با سطح مقطع دایره‌ای شکل قابل استفاده است؛ در حالی که رابطه پیچش، برای میله‌های توپر و همچنین لوله‌های دایره‌ای کاربرد دارد. رابطه بالا، ارتباط غیر مستقیم بین تنش برشی و توان سوم قطر را نمایش می‌دهد. بنابراین، اگر قطر میله دو برابر شود، تنش برشی درون آن یک‌هشتم خواهد شد. تنش برشی موجود در فاصله شعاعی ρ با استفاده از رابطه زیر تعیین می‌شود:

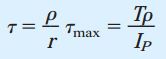
این رابطه از ترکیب τ=ρτ_max/r با رابطه پیچش به دست می‌آید و با عنوان «رابطه کلی پیچش» (Generalized Torsion Formula) شناخته می‌شود. در اینجا نیز رابطه بین تنش‌های برشی و فاصله شعاعی به صورت خطی است.

در سیستم SI، گشتاور پیچشی T با واحد نیوتن بر متر (N.m)، شعاع r با واحد متر (m)، ممان اینرسی قطبی I_P با واحد متر به توان چهار (m⁴) و تنش برشی τ با واحد پاسکال (Pa) بیان می‌شود. واحد این کمیت‌ها در سیستم یکاهای آمریکایی به ترتیب برابر با پوند-فوت (lb-ft) یا پوند-اینچ (lb-in)، اینچ (in)، اینچ به توان چهار (in⁴) و پوند بر اینچ مربع (psi) است.

زاویه پیچش

اکنون می‌توانیم رابطه بین زاویه پیچش یک میله الاستیک خطی و گشتاور پیچشی اعمال شده را نمایش دهیم. با ادغام روابط τ_max=Gr_θ و τ_max=Tr/I_P، خواهیم داشت:

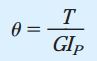
θ، بر حسب رادیان بر واحد طول بیان می‌شود. بر اساس رابطه بالا، نرخ زاویه پیچش با گشتاور پیچشی رابطه مستقیم و با صلبیت پیچشی (GI_P) رابطه عکس دارد. برای یک میله تحت پیچش خالص، زاویه پیچش کل φ از حاصل‌ضرب نرخ زاویه پیچ در طول میله به دست می‌آید (φ=θL). بنابراین:

اندازه‌گیری φ بر حسب رادیان صورت می‌گیرد. کمیت GI_P/L با عنوان «سختی پیچشی» (Torsional Stiffness) شناخته می‌شود. این کمیت، گشتاور پیچشی مورد نیاز برای دوران میله به اندازه یک واحد زاویه را نمایش می‌دهد. معکوس سختی پیچشی یا L/GI_P نیز با عنوان «انعطاف‌پذیری پیچشی» (Torsional Flexibility) شناخته می‌شود. این کمیت، بیانگر زاویه دوران ناشی از اعمال یک واحد گشتاور پیچشی است. به این ترتیب:

این کمیت‌ها معادلِ سختی محوری (k=EA/L) و انعطاف‌پذیری محوری (f=L/EA) در یک میله تحت کشش یا فشار هستند. سختی‌ها و انعطاف‌پذیری‌ها نقش بسیار مهمی را در تحلیل سازه‌ها بازی می‌کنند. یکی از کاربردهای رابطه زاویه پیچش، تعیین مدول برشی ماده است. به این منظور، با انجام آزمایش پیچش بر روی یک میله دایره‌ای و اندازه‌گیری زاویه پیچش ناشی از اعمال گشتاور T، مقدار مدول برشی ماده محاسبه می‌شود.

لوله‌های دایره‌ای

لوله‌های دایره‌ای برای مقاومت در برابر اعمال بارهای پیچشی نسبت به میله‌های توپر بهره‌وری بیشتری برخوردار هستند. همان طور که می‌دانیم، تنش برشی بر روی سطح خارجی یک میله دایره‌ای توپر دارای مقدار ماکسیمم و در مرکز میله دارای مقدار صفر است. از این‌رو هنگام اعمال بارهای پیچشی، حجم زیادی از ماده تشکیل‌دهنده میله‌های توپر در معرض تنش‌های بسیار کوچک‌تر از تنش برشی ماکسیمم قرار دارد. علاوه بر این، به دلیل کوچک بودن بازوی گشتاوری (ρ) در نزدیکی مرکز میله، امکان تعیین گشتاور پیچشی در این نقاط وجود ندارد.

هندسه لوله‌های دایره‌ای به گونه‌ای است که اکثر مواد تشکیل‌دهنده آن‌ها در نزدیکی سطح خارجی قرار دارند. در این نواحی، مقدار تنش‌های برشی و بازوی گشتاوری به بیشترین حد خود می‌رسد. بنابراین، در صورت اهمیت داشتن مسئله کاهش وزن و صرفه‌جویی در مواد، استفاده از لوله‌های دایره‌ای در شرایط بارگذاری پیچشی کاربرد بیشتری خواهد داشت.

به عنوان مثال، میل‌لنگ‌های بزرگ، میل کاردان‌ها و محور توربین‌ها معمولاً دارای سطح مقطع دایره‌ای توخالی هستند. تحلیل پیچش یک لوله دایره‌ای تقریباً مشابه تحلیل میله‌های توپر است. روابط ارائه شده برای تعیین تنش‌های برشی در میله‌ها را می‌توان برای لوله‌ها نیز استفاده کرد. با این تفاوت که فاصله شعاعی (ρ) لوله‌ها در محدوده r₁ (شعاع داخلی) تا r₂ (شعاع خارجی) قرار می‌گیرد.

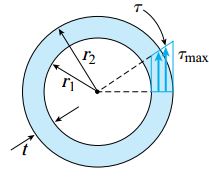
در بخش‌های قبلی رابطه بین گشتاور پیچشی T و تنش برشی ماکسیمم به صورت یک انتگرال بیان شد. در این بخش، به منظور تعیین ممان اینرسی قطبی باید حدود انتگرال را برابر با ρ=r₁ و ρ=r₂ قرار داد. به این ترتیب، ممان اینرسی قطبی برای مساحت سطح مقطع لوله با استفاد از رابطه زیر تعیین خواهد شد:

این رابطه را می‌توان به صورت زیر نیز نوشت:

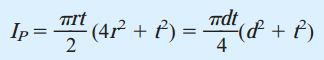
• r: شعاع میانگین برابر با r₁+r₂)/2)
• d: قطر میانگین برابر با d₁+d₂)/2)
• t: ضخامت دیواره برابر با r₂-r1

نتایج به دست آمده از دو رابطه بالا برابر خواهند بود اما در برخی از مواقع، استفاده از رابطه دوم ساده‌تر است. اگر ضخامت دیواره لوله در مقایسه با شعاع میانگین آن کوچک باشد، می‌توانیم از عبارت t₂ در رابطه دوم صرف نظر کنیم. به این ترتیب، رابطه تقریبی ممان اینرسی قطبی به شکل زیر درمی‌آید:

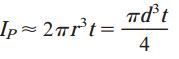
به خاطر داشته باشید که کمیت‌های r و d بیانگر مقادیر میانگین شعاع و قطر هستند و مقادیر ماکسیمم را نمایش نمی‌دهند. به همین دلیل، رابطه بالا به عنوان یک تخمین و روابط قبلی به عنوان محاسبات دقیق در نظر گرفته می‌شوند. رابطه پیچش (τ_max=Tr/I_P) را می‌توان برای یک لوله دایره‌ای شکل با رفتار الاستیک خطی نیز مورد استفاده قرار داد.

در این صورت، مقادیر I_P را می‌توان ز طریق روابط بالا محاسبه کرد. این موضوع برای رابطه کلی تنش برشی (τ=Tρ/I_P)، نرخ پیچش (θ=T/GI_P)، زاویه پیچش (φ=TL/GI_P)، سختی (KT=GI_P/L) و انعطاف‌پذیری (fT=L/GI_P) نیز صدق می‌کند.

شکل زیر، توزیع تنش برشی در یک لوله را نمایش می‌دهد. با توجه به شکل، مشاهده می‌کنیم که مقدار تنش میانگین در یک لوله نازک تقریباً به اندازه تنش ماکزیمم است. این موضوع بر کارآمدتر بودن نحوه به کارگیری مواد در میله‌های توخالی نسبت به میله‌های توپر دلالت می‌کند (مثال‌های 2 و 3 در انتهای مقاله).

در هنگام طراحی یک لوله دایره‌ای به منظور انتقال گشتاورهای پیچشی، باید از مناسب بودن میزان ضخامت دیواره اطمینان حاصل کرد. توجه به این موضوع باعث جلوگیری از چین‌خوردگی و کمانش دیواره لوله می‌شود. به این منظور، معمولاً یک مقدار ماکسیمم برای نسبت شعاع به ضخامت، مانند 12=r₂/t مورد استفاده قرار می‌گیرد. اثرات محیطی و عوامل مرتبط با دوام نیز به عنوان ملاحظات طراحی در نظر گرفته می‌شوند. این عوامل می‌توانند بر روی تعیین ضخامت حداقلی برای دیواره لوله تأثیرگذار باشند.

نکات تکمیلی

معادلات ارائه شده در این مقاله برای میله‌های دایره‌ای شکل (توپر یا توخالی) با رفتار الاستیک خطی قابل استفاده هستند. به عبارت دیگر، بارگذاری‌ها باید به گونه‌ای باشند که ماده از حد الاستیک خود عبور نکند. علاوه بر این، معادلات تنش تنها برای مقاطع دور از نواحی تمرکز تنش (مانند حفره‌ها) و دور از نقاط بارگذاری اعتبار دارند. در پایان باید تأکید کنیم که معادلات ارائه شده برای میله و لوله‌های دایره‌ای شکل را نمی‌توان برای میله‌های غیر دایره‌ای مورد استفاده قرار داد.

به عنوان مثال، رفتار میله‌هایی با سطح مقطع مستطیلی یا I شکل در مقایسه با میله‌های دایره‌ای کاملاً متفاوت است. سطح مقطع این نوع میله‌ها در اثر اعمال بارهای پیچشی ثابت باقی نمی‌ماند. به علاوه، تنش‌های ماکسیمم در آن‌ها بر روی دورترین نقطه از مرکزِ سطحِ مقطع قرار ندارد. با توجه به این نکات، تحلیل میله‌های غیر دایره‌ای نیازمند به کارگیری روش‌های پیشرفته‌تر است.

مثال‌ها

در این بخش، به منظور آشنایی بهتر با مؤلفه‌های تنش در شرایط بارگذاری پیچشی و نحوه استفاده از روابط ارائه شده در بخش‌های قبلی برای تعیین این مؤلفه‌ها، به تشریح چند مثال می‌پردازیم.

مثال 1

شکل زیر، یک میله توپر با سطح مقطع دایره‌ای شکل، قطر 1.5 اینچ، طول 54 اینچ و مدول برشی 11.5x10⁶ پوند بر اینچ مربع را نمایش می‌دهد. اگر گشتاور پیچشی T=250lb-ft به دو انتهای میله اعمال شود، کمیت زیر چقدر خواهند بود؟ (تنش برشی مجاز را τ_allow=6000psi و زاویه پیچش مجاز را ^◦φ_allow=2.5 در نظر بگیرید.)

• الف) تنش برشی ماکسیمم و زاویه پیچش بین دو انتهای میله
• ب) حداکثر گشتاور پیچشی مجاز

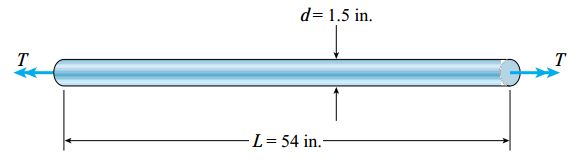
الف) تعیین تنش برشی ماکسیمم و زاویه پیچش

به دلیل توپر بودن سطح مقطع میله، تنش برشی ماکسیمم با استفاده از رابطه زیر به دست می‌آید:

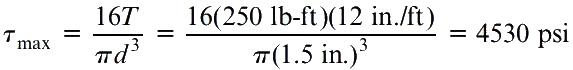
زاویه پیچش نیز توسط روابط زیر تعیین می‌شود:

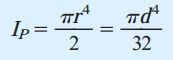
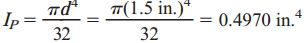
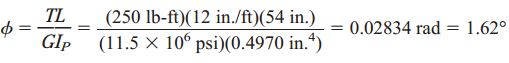
ب) حداکثر گشتاور پیچشی مجاز

مقدار حداکثر گشتاور پیچشی مجاز را می‌توان با استفاده از تنش برشی مجاز یا زاویه پیچش محاسبه کرد. برای این منظور، ابتدا رابطه τ_max را بر حسب T بازنویسی می‌کنیم:

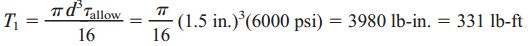
اگر میزان گشتاور پیچشی اعمال شده از T₁ بیشتر شود، تنش برشی ایجاد شده از مقدار مجاز 6000psi عبور می‌کند. با بازنویسی رابطه φ بر حسب T، مقدار گشتاور پیچشی را با توجه به مقدار زاویه پیچش به دست می‌آید:

اگر میزان گشتاور پیچشی اعمال شده از T₂ بیشتر شود، زاویه پیچش از مقدار مجاز 2.5 درجه عبور می‌کند. از بین T₁ و T₂، مقدار کمتر به عنوان حداکثر گشتاور پیچشی مجاز انتخاب می‌شود:

در این مثال، محدودیت مسئله توسط تنش برشی مجاز کنترل می‌شود.

مثال 2

قرار است که از یک شَفت فولادی برای تولید یک میله دایره‌ای توپر یا یک لوله دایره‌ای استفاده شود (شکل زیر). وظیفه این شفت، انتقال گشتاور پیچشی 1200 نیوتن در متر (N.m) را بدون عبور از تنش برشی مجاز 40 مگا پاسکال (MPa) و نرخ مجاز پیچش 0.75 درجه بر متر (m/◦) است. با در نظر گرفتن مدول برشی 78 گیگا پاسکال (GPa)، کمیت‌های زیر را تعیین کنید.

• الف) قطر مورد نیاز برای شفت توپر
• ب) قطر مورد نیاز برای شفت توخالی (ضخامت دایره شفت برابر با یک‌دهم قطر خارجی آن است.)
• ج) نسبت قطرها (d₂/d₀) و نسبت وزن‌های شفت توخالی و شفت توپر

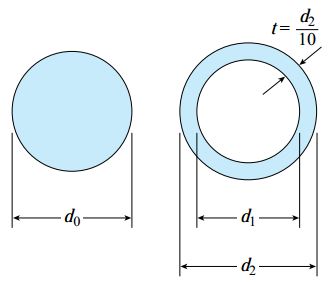
الف) شفت توپر

قطر مورد نیاز d₀ را می‌توان با استفاده از تنش برشی مجاز یا نرخ مجاز پیچش تعیین کرد. با بازنویسی رابطه پایین بر حسب d، قطر مورد نیاز با توجه به تنش برشی مجاز محاسبه می‌شود:

بنابراین:

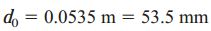
برای تعیین قطر مورد نیاز با توجه به نرخ مجاز پیچش باید ممان اینرسی قطبی را محاسبه کنیم:

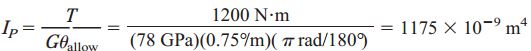
ممان اینرسی قطبی از با رابطه πd⁴/32 نیز برابر است. به این ترتیب، قطر مورد نیاز با توجه به نرخ مجاز پیچش به صورت زیر تعیین می‌شود:

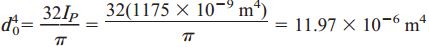
در نتیجه:

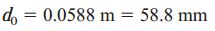
با مقایسه مقادیر به دست آمده برای d₀، مشاهده می‌کنیم که نرخ پیچش باید به عنوان عامل تعیین‌کننده طراحی در نظر گرفته شود. به این ترتیب، قطر مورد نیاز برای شفت توپر برابر است با:

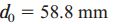
در طراحی‌های واقعی، قطر انتخاب‌شده برای میله کمی بزرگ‌تر از مقدار به دست آمده برای d₀ خواهد بود (مانند 60 میلی‌متر).

ب) شفت توخالی

محاسبه قطر مورد نیاز برای شفت توخالی نیز بر اساس مقادیر تنش برشی مجاز یا نرخ مجاز پیچش صورت می‌گیرد. به این منظور، محاسبات خود را با در نظر گرفتن قطر خارجی میله (d₂) و تعیین قطر داخلی میله (d₁) به صورت زیر شروع می‌کنیم:

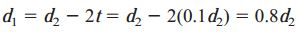
ممان اینرسی قطبی، با استفاده از رابطه زیر به دست می‌آید:

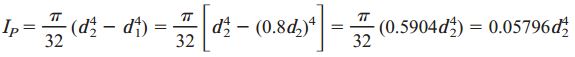
برای تعیین تنش برشی مجاز، τ_allow را به جای τ درون رابطه پیچش قرار می‌دهیم:

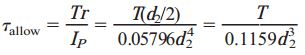
با بازنویسی رابطه با بر حسب قطر خارجی، به رابطه زیر می‌رسیم:

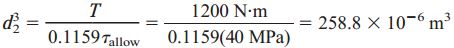
بنابراین:

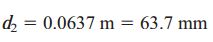
این مقدار، قطر خارجی مورد نیاز با توجه به تنش برشی مجاز است. برای تعیین نرخ مجاز پیچش، با جایگذاری I_P به دست آمده از مراحل قلبی در رابطه نرخ پیچش و قرار دادن θ_allow به جای θ خواهیم داشت:

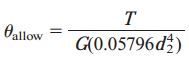
با بازنویسی رابطه بر حسب قطر خارجی، به رابطه زیر می‌رسیم:

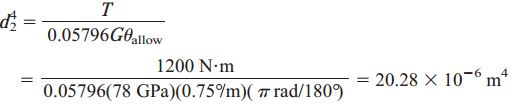
این مقدار، قطر خارجی مورد نیاز با توجه به تنش برشی مجاز را نمایش می‌دهد. با مقایسه مقادیر به دست آمده برای d₂، مشاهده می‌کنیم که در این مسئله باید طراحی‌ها را بر اساس نرخ پیچش اجرا کرد. به این ترتیب، قطر خارجی مورد نیاز برای شفت توخالی برابر است با:

ج) نسبت قطرها و وزن‌ها

نسبت مقادیر به دست آمده برای قطر خارجی شفت توخالی به قطر شفت توپر، به صورت زیر تعیین می‌شود:

به دلیل رابطه مستقیم بین وزن شفت‌ها و مساحت سطح مقطعشان، برای تعیین نسبت وزن شفت توخالی به وزن شفت توپر می‌توانیم از نسبت مساحت‌ها استفاده کنیم:

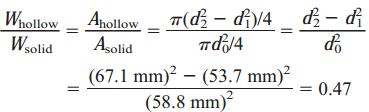
با توجه به نتایج، برای ساخت شفت توخالی به 47 درصد از مواد تشکیل‌دهنده شفت توپر نیاز است؛ در صورتی که قطر خارجی شفت توخالی تنها 14 درصد بزرگ‌تر از قطر خارجی شفت توپر است.

توجه: در این مثال، نحوه تعیین ابعاد مورد نیاز برای میله‌های توپر و لوله‌های دایره‌ای بر اساس مقادیر تنش‌های مجاز و نرخ‌های مجاز پیچ نمایش داده شد. علاوه بر این، با توجه به نتایج به دست آمده مشاهده کردیم که نحوه به کارگیری مواد در ساخت لوله‌های دایره‌ای کارآمدتر از میله‌های توپر است.

مثال 3

شکل زیر، یک شفت توخالی و یک شفت توپر با مواد سازنده، طول و شعاع خارجی یکسان را نمایش می‌دهد. شعاع داخلی شفت توخالی برابر با 0.6R است.

• الف) با فرض اعمال گشتاور پیچشی برابر به هر دو شفت، تنش‌های برشی، زوایای پیچش و وزن هر یک را با هم مقایسه کنید.
• ب) نسبت مقاومت به وزن را برای هر دو شفت به دست آورید.

الف) مقایسه تنش‌های برشی

به دلیل برابر بودن گشتاور پیچشی و شعاع شفت توخالی و توپر، برای مقایسه تنش‌های برشی باید از ممان اینرسی قطبی استفاده کنیم. بر اساس رابطه پیچش، تنش برشی ماکسیمم با I_P رابطه عکس دارد. ممان اینرسی قطبی برای شفت توخالی به صورت زیر تعیین می‌شود:

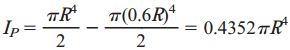
رابطه I_P برای شفت توپر نیز به صورت زیر است:

به این ترتیب، نسبت تنش برشی ماکسیمم شفت توخالی (τ_H) به تنش برشی ماکسیمم شفت توپر (τ_S) برابر است با:

مقایسه زاویه پیچش

به دلیل برابر بودن گشتاور پیچشی، طول و مدول برشی شفت توخالی و توپر، برای مقایسه زاویه پیچش نیز باید از ممان اینرسی قطبی استفاده کنیم. بر اساس رابطه زاویه پیچش، این زاویه با I_P رابطه عکس دارد. نسبت زاویه پیچش شفت توخالی (φ_H) به زاویه پیچش شفت توپر (φ_S) برابر است با:

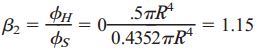
مقایسه وزن‌ها

وزن شفت‌ها با مساحت سطح مقطعشان رابطه مستقیم دارد. بنابراین، وزن شفت توپر با رابطه πR² و وزن شفت توخالی با رابطه زیر متناسب خواهد:

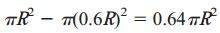
به این ترتیب، نسبت وزن شفت توخالی (W_H) به وزن شفت توپر (W_S) برابر است با:

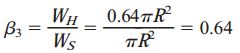
بر اساس این نتایج مشاهده می‌شود که تنش و زاویه پیچش به وجود آمده در شفت توخالی به اندازه 15 درصد بیشتر از تنش و زاویه پیچش شفت توپر است اما شفت توخالی نسبت به شفت توپر 36 درصد وزن کمتری دارد. این موضوع، یکی از مزیت‌های ذاتی شفت‌های توخالی نسبت به شفت‌های توپر را نمایش می‌دهد.

ب) نسبت مقاومت به وزن

در برخی از مواقع، بهره‌وری و کارآمد بودن یک سازه با استفاده از «نسبت مقاومت به وزن» (Strength to Weight Ratio) مورد سنجش قرار می‌گیرد. برای یک میله تحت پیچش، این نسبت با تقسیم گشتاور پیچش مجاز بر وزن میله به دست می‌آید. گشتاور پیچشی مجاز در شفت توخالی (T_H) به صورت زیر تعیین می‌شود:

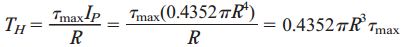
گشتاور پیچشی مجاز در شفت توپر (T_S) نیز توسط رابطه زیر به دست می‌آید:

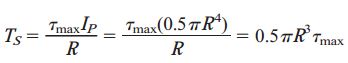
به منظور تعیین وزن هر شفت، مساحت سطح مقطع آن‌ها را در طول L و وزن مخصوص γ ضرب می‌کنیم:

نسبت مقاومت به وزن S_H و S_S به ترتیب برای شفت توخالی و توپر به صورت زیر خواهد بود:

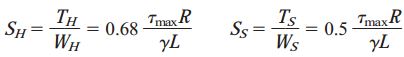
در این مثال، نسبت مقاومت به وزن در شفت توخالی 36 درصد بیشتر از این نسبت برای شفت توپر است. این مسئله، بهره‌وری بیشتر شفت توخالی در مقایسه با شفت توپر را نمایش می‌دهد. برای شفت‌های نازک‌تر، این اختلاف بیشتر و برای شفت‌های ضخیم‌تر، این اختلاف کمتر خواهد بود.

^^