رابطه و تابع از نگاه مجموعه‌ ها – به زبان ساده

در نوشتارهای دیگر فرادرس با عنوان مجموعه ها در ریاضیات – مفاهیم پایه  و ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده، با مفهوم مجموعه، زوج مرتب و ضرب دکارتی دو مجموعه آشنا شدیم. با فرض اینکه A و B دو مجموعه غیر تهی هستند، می‌خواهیم به بررسی زیر مجموعه‌هایی از $$A\times B$$ بپردازیم که دارای خصوصیات جالبی هستند. این زیر مجموعه‌ها ممکن است در حالت کلی، یک «رابطه» (Relation) از A به B و در حالت خاص یک تابع از A به B باشند. گاهی تابع را یک «نگاشت» (MAP) از A به B نیز می‌نامند.

در این نوشتار به بررسی رابطه و تابع می‌پردازیم که زیر مجموعه‌هایی از ضرب دکارتی دو مجموعه محسوب می‌شوند. بنابراین فرض می‌کنیم که با مفهوم زیر مجموعه، عضو و دیگر ویژگی‌های مجموعه‌ها آشنایی دارید. برای درک بهتر این مفاهیم پیشنهاد می‌شود مطلب‌هایی که در بالا به آن‌ها اشاره شد را مطالعه کنید. همچنین مطالعه گزاره ها و سورهای منطقی — به زبان ساده و ترکیب گزاره های منطقی — به زبان ساده نیز خالی از لطف نیست.

رابطه و تابع

فرض کنید A و B دو مجموعه غیر تهی و C نیز مجموعه‌ای باشد که از حاصلضرب دکارتی آن دو ساخته شده است.

فیلم آموزش مبانی منطق و نظریه مجموعه ها در فرادرس

کلیک کنید

به این ترتیب داریم:

$$C=A\times B =\{(x,y)|x\in A , y\in B\}$$

مشخص است که تعداد اعضای مجموعه C برابر با حاصلضرب تعداد اعضای مجموعه A در B‌ است. بنابراین اگر تعداد اعضای مجموعه A, B, C را با |A| ،|B| و |C| نشان دهیم خواهیم داشت:

$$|C|=|A|\times |B|$$

اگر همه زیر مجموعه‌های C را در یک مجموعه قرار دهید، مجموعه توانی C را تولید کرده‌اید که آن را با $$P(C)$$ نشان می‌دهند. البته می‌دانیم که تهی نیز یکی از این زیرمجموعه‌ها است. برای مثال اگر $$D=\{1,2,3\}$$ باشد، مجموعه توانی آن به صورت زیر نوشته می‌شود.

$$P(D)=\{\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\},\emptyset\}$$

براساس رابطه‌ای که بین تعداد اعضای یک مجموعه (مثل D) و تعداد زیرمجموعه‌هایش وجود دارد، می‌دانیم که تعداد اعضای مجموعه توانی برابر با $$2^{|D|}$$ است. بنابراین تعداد زیرمجموعه‌های D برابر است با $$2^3=8$$. به همین ترتیب تعداد همه زیرمجموعه‌های غیر تهی از D برابر با $$2^{|D|}-1$$ خواهد بود.

تعریف رابطه (Relation)

با توجه به تعریف مجموعه توانی و ضرب دکارتی دو مجموعه A و B که به صورت $$|C|=|A|\times |B|$$ نوشته شد، «رابطه» (Relation) را هر عضو غیرتهی از مجموعه $$P(C)$$ می‌توان در نظر گرفت. به این ترتیب می‌توان گفت: هر زیر مجموعه‌‌ای غیرتهی از ضرب دکارتی دو مجموعه یک رابطه است.

معمولا رابطه را با حروف R یا S نشان می‌دهند. در این حالت می‌گویم R یک رابطه از A به B‌ است اگر R زیرمجموعه غیرتهی از $$A\times B$$ باشد. به بیان ریاضی خواهیم داشت:

$$R\subset A\times B ,\;\;R\neq \emptyset$$

با توجه به مفهوم زوج مرتب و ضرب دکارتی دو مجموعه مشخص است که اگر R یک رابطه از A به B باشد، لزوما با رابطه S که یک رابطه از B به A نامیده می‌شود، برابر نیست. پس خاصیت جابجایی برای رابطه وجود ندارد. به بیان ریاضی:

$$R\subset A\times B \neq S\subset B\times A$$

مثال

فرض کنید مجموعه A از اسامی حیوانات وحشی و مجموعه B نیز شامل مجموعه اسامی غذای آن‌ها باشد. با استفاده از یک نمودار، سعی می‌کنیم، رابطه بین این دو مجموعه را نشان دهیم. رابطه هر عضو از مجموعه حیوانات با مجموعه غذاها بوسیله یک خط مشخص شده است. همانطور که دیده می‌شود، ممکن است عضوی از مجموعه اول با هیچ عضوی از مجموعه دوم در ارتباط نباشد. همچنین ممکن است عضوی از مجموعه اول مانند خرس با دو عضو از مجموعه دوم مثل عسل و گوشت در رابطه باشد.

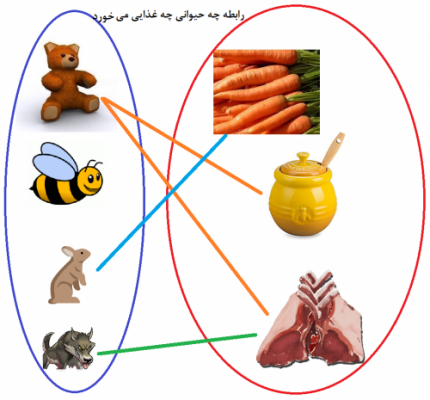
اگر «رابطه چه حیوانی چه غذایی می‌خورد» را با علامت R نشان دهیم، اعضای این رابطه به صورت مجموعه {(خرس، عسل)، (خرس، گوشت)، (خرگوش، هویج)، (گرگ، گوشت)}=R نوشته می‌شود. البته این رابطه برای زوج مرتب را گاهی به صورت «عسلRخرس» نیز می‌نویسند و می‌خوانند: «خرس در رابطه R با عسل است». البته مشخص است که منظور از این رابطه، عبارت «خرس، عسل را می‌خورد» به بیان زبان فارسی است.

به عنوان مثال دیگر می‌توان به دایره اشاره کرد. براساس تعریف می‌دانیم: «دایره، مکان هندسی نقاطی است که از یک نقطه (مرکز) دارای فاصله ثابت و برابر هستند». از لحاظ ریاضی، دایره می‌تواند یک رابطه بین نقاط مختصات دکارتی تلقی شود زیرا اگر x را طول و y را عرض نقاط در مختصات دکارتی در نظر بگیریم، رابطه بین آن‌ها را می‌توان به صورت $$x^2+y^2=r^2$$ نوشت که در آن r شعاع دایره است.

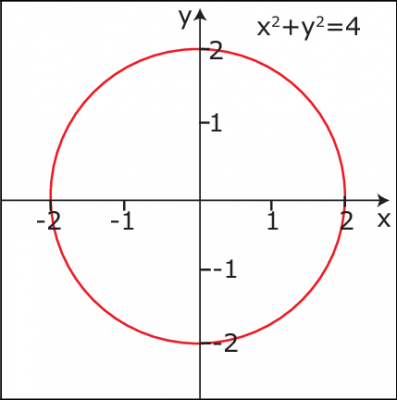
برای مثال اگر r=2 باشد، بعضی از نقاطی که در رابطه دایره صدق می‌کنند به صورت (0,2), (2-,0), (2,0-), (2,0) نوشته می‌شوند. البته بقیه نقاط را براساس مقدار دهی به x و محاسبه y می‌توان بدست آورد. به این ترتیب با اتصال این نقطه‌ها، دایره ترسیم می‌شود.

رابطه بین چند مجموعه

می‌توان تعریف رابطه را گسترش داده و براساس ضرب دکارتی n مجموعه نوشت. به این ترتیب رابطه R به صورت «چندتایی مرتب» (Tuples) معرفی می‌شود. در این حالت خواهیم داشت:

$$(x_1,x_2,\cdots ,x_n) \in R\subset A_1\times A_2\times\cdots \times A_n$$

برهمین اساس می‌توان کره را یک رابطه در مختصات سه بعدی در نظر گرفت. این رابطه برای کره‌ای با شعاع r و به مرکز (0,0,0) به صورت $$x^2+y^2+z^2=r^2$$ نوشته می‌شود که x را طول، y‌ را عرض و z را ارتفاع نقطه در نظر می‌گیرند.

دامنه و هم دامنه

اگر رابطه R از A به B تعریف شده باشد، مجموعه مقادیر مولفه‌های اول زوج‌های مرتب مربوط به رابطه R را «دامنه» (Domain) آن رابطه می‌گویند و با $$D_R$$ نشان می‌دهند. به بیان ریاضی دامنه رابطه R را به صورت زیر تعریف می‌کنند.

$$D_R=\{x; \;(x,y)\in R\}$$

به همین ترتیب مجموعه مقادیر مولفه‌های دوم زوج مرتب‌هایی که در رابطه R قرار دارند، «هم‌دامنه» (Co-Domain) نامیده می‌شود. گاهی به هم‌دامنه، «برد» (Range) نیز می‌گویند و با $$R_R$$ نشان داده می‌شود.

$$R_R=\{y; \;(x,y)\in R\}$$

انواع رابطه

در ادامه به معرفی و بررسی چند نوع رابطه می‌پردازیم که بخصوص در ریاضیات گسسته به کار می‌رود. در اینجا برای نمایش رابطه بین زوج‌های مرتب (x,y) از ماتریسی به صورت زیر استفاده می‌کنیم.

فیلم آموزش مجموعه روابط تابع در ساختمان گسسته (رایگان) در فرادرس

کلیک کنید

مقدارهای ۱ درون ماتریس نشان دهنده وجود رابطه و مقدار ۰ نشانگر عدم رابطه بین مقدارهای سطر و ستون ماتریس است.

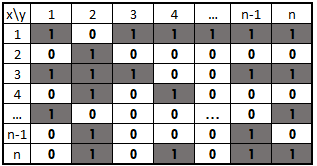
رابطه بازتابی (Reflexive Relation)

در این نوع رابطه، هر مجموعه با خودش در رابطه است. اگر این رابطه را با I نشان دهیم، می‌توان نوشت:

$$I=\{(x,x)| x\in A\}$$

به این ترتیب، ماتریس رابطه بازتابی به صورت زیر خواهد بود. گاهی به رابطه بازتابی، «رابطه همانی» یا «رابطه انعکاسی» نیز گفته می‌شود.

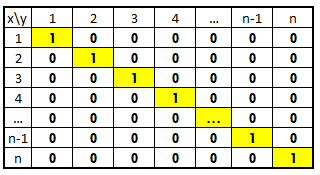
برای مثال اگر $$A=\{1,2,3\}$$ باشد، آنگاه $$I=\{(1,1),(2,2),(3,3)\}$$ یک رابطه بازتابی است.

رابطه تقارنی (Symmetric Relation)

رابطه S را یک رابطه تقارنی روی A گویند اگر دوتایی مرتب (x,y) در رابطه S باشند، حتما زوج (y,x) هم در S باشند. به بیان ریاضی می‌توان گفت:

$$\forall x,y \in A ;\; xSy \leftrightarrow ySx$$

به این ترتیب، ماتریس رابطه تقارنی به صورت زیر خواهد بود. در این جدول، خانه‌هایی که دارای رنگ مشابه هستند با یکدیگر رابطه تقارنی دارند.

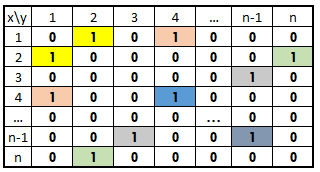
رابطه «=» در اعداد یک رابطه تقارنی است، زیرا اگر $$2^2=4$$ باشد آنگاه $$4=2^2‌$$ است. اگر یک رابطه دارای زوج‌های مرتب متقارن نباشد، آن را «نامتقارن» (Asymmetric) می‌نامند. به این معنی که اگر x با y‌ در رابطه باشد، آنگاه y با x در رابطه نخواهد بود. بنابراین اگر از عبارت $$x \not Sy$$ به معنی عدم رابطه $$S$$ بین $$x$$ و $$y$$ استفاده کنیم، به بیان ریاضی خواهیم داشت:

$$\forall x,y \in A ;\; xSy \leftrightarrow x \not Sy$$

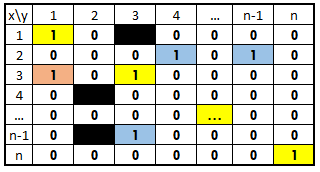
در ماتریس بالا، خانه‌های با رنگ سیاه، بیانگر محل‌هایی هستند که نمی‌توانند در رابطه نامتقارن وجود داشته باشند.

رابطه پادتقارنی (Anti-Symmetric Relation)

رابطه S را یک رابطه پادتقارنی روی A گویند اگر (x,y) و (y,x) هر دو در S باشند، نتیجه بگیریم که x=y است. به بیان ریاضی می‌توان گفت:

$$\forall x,y \in A ;\; xSy \wedge ySx \leftrightarrow x=y$$

به این ترتیب، فقط زمانی می‌توان اعضای متقارن در رابطه پادتقارنی پیدا کرد که مولفه اول و دوم با یکدیگر برابر باشند. ماتریس زیر بیانگر یک مثال از رابطه پادتقارنی برای مجموعه اعداد ۱ تا n است.

نکته: حتما به یاد دارید که در ترکیب گزاره‌های منطقی منظور از $$\wedge$$، ترکیب عطفی دو گزاره است که آن را به صورت «و» می‌خوانند.

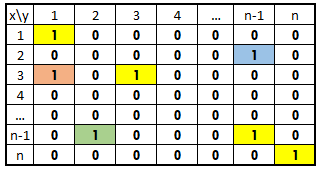
رابطه ترایا (Transitive Relation)

رابطه R را یک رابطه ترایا یا تراگذری گویند اگر برای سه عضو از مجموعه A، مثل x,y,z بتوان نوشت:

$$\forall x,y,z\in A:(xRy\wedge yRz)\Rightarrow xRz$$

به این ترتیب، ماتریس رابطه ترایایی به صورت زیر خواهد بود. در این جدول، خانه‌هایی که دارای رنگ مشابه هستند با یکدیگر رابطه ترایایی دارند. رابطه ترایا را گاهی رابطه تعدی نیز می‌نامند.

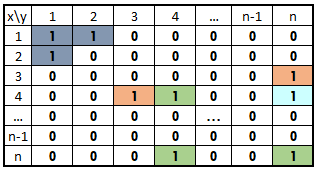
با توجه به این تعریف، مشخص است با فرض ترایا بودن رابطه R، اگر دو زوج (۱،۲) و (۲،۱) در رابطه R باشند، آنگاه زوج (۱،۱) نیز باید در R باشند. به بیان ریاضی خواهیم داشت:

$$(1,2)\in R \wedge (2,۱)\in R \Rightarrow (1,۱)\in R$$

رابطه هم‌ارزی (Equivalence)

رابطه R را یک رابطه هم‌ارزی می‌گویند اگر و فقط اگر شرط‌های زیر برایش برقرار باشد:

1. رابطه R یک رابطه بازتابی باشد. یعنی برای هر عضوی مثل x از A داشته باشیم $$(x,x)\in R$$
2. رابطه R یک رابطه تقارنی باشد. یعنی برای هر دو عضوی مثل x و y از A داشته باشیم $$(x,y) \in R , (y,x)\in R$$
3. رابطه R یک رابطه ترایا باشد. یعنی برای سه عضو از مجموعه A، مثل x,y,z بتوان نوشت: $$(xRy \wedge yRz) \Rightarrow xRz$$.

از آنجایی که گزاره به صورت دو شرطی (اگر و فقط اگر) نوشته شده است، متوجه می‌شویم که اگر سه شرط برقرار باشند، رابطه هم‌ارزی است و اگر رابطه هم‌ارزی باشد، حتما سه شرط برقرار است.

به این ترتیب، ماتریس رابطه هم‌ارزی به صورت زیر خواهد بود. مشخص است که اعضای این ماتریس همگی در سه شرط مربوط به رابطه هم‌ارزی صدق می‌کنند.

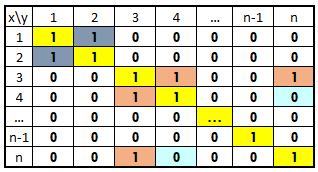
مشخص است که رابطه تساوی در ریاضی که با «=» نشان داده می‌شود، یک رابطه هم‌ارزی است. همچنین رابطه «توازی» (Parallel) یا «تشابه» (Similar) نیز رابطه‌های هم‌ارزی هستند.

رابطه ترتیبی (Order)

رابطه R را یک رابطه ترتیبی گویند، اگر و فقط اگر شرط‌های زیر برایش برقرار باشد.

1. رابطه R یک رابطه بازتابی باشد. یعنی برای هر عضو از مجموعه A، مثل x داشته باشیم؛ $$xRx$$
2. رابطه R یک رابطه ترایا باشد. یعنی برای سه عضو از مجموعه A، مثل x,y,z بتوان نوشت: $$(xRy \wedge yRz) \Rightarrow xRz$$.
3. رابطه R یک رابطه پادتقارنی باشد. یعنی برای هر دو عضو از مجموعه A مثل x,y داشته باشیم: $$(xRy \wedge yRx) \leftrightarrow x=y$$

برای مثال، رابطه «کوچکتر یا مساوی» یک رابطه ترتیبی روی مجموعه اعداد حقیقی است. فرض کنید مجموعه A اعداد حقیقی باشد، در این حالت می‌دانیم رابطه $$\leq$$ بازتابی است. زیرا $$x\leq x$$. از طرفی این رابطه ترایا است. زیرا می‌توان نوشت:

$$(x\leq y) \wedge (y \leq z) \rightarrow x\leq z$$

از طرف دیگر رابطه $$\leq$$ پادتقارنی نیز هست زیرا می‌توان به راحتی تحقیق کرد که رابطه زیر برای اعداد حقیقی برقرار است:

$$(x\leq y) \wedge (y \leq x) \rightarrow x= y$$

تعریف تابع (Function)

از نگاه نظریه مجموعه‌ها، تابع یک رابطه است که باید در یک شرط صدق کند. این شرط به صورت زیر بیان می‌شود. تابع، رابطه‌ای است که هیچ عضوی از آن دارای مولفه اول یکسان نباشد.

فیلم آموزش کاربرد روابط و توابع در ریاضیات (برای مدیریت، حسابداری و اقتصاد) (رایگان) در فرادرس

کلیک کنید

به این ترتیب اگر F را یک تابع در نظر بگیریم، این نگارش را می‌توان به بیان ریاضی، طبق رابطه زیر نوشت:

$$\forall (x,y) , (x',y') \in F\; ;\;\; x=x' \rightarrow y=y'$$

همانطور که دیده می‌شود طبق این تعریف می‌توان گفت، اگر برای هر دو عضوی از اعضای رابطه F، مولفه‌های اول یکسان باشند باید نتیجه گرفت که مولفه‌های دوم نیز یکسان هستند. به این ترتیب عضو (x,y) با عضو ('x,'y) تفاوتی ندارد. پس چون در مجموعه، اعضای تکراری را فقط یکبار ذکر می‌کنیم، در مجموعه حاصل از رابطه F فقط یکبار عضو (x,y) نوشته می‌شود. پس رابطه F یک تابع خواهد بود.

این تعریف را می‌توان بر اساس عکس نقیض گزاره شرطی نیز نوشت. به این ترتیب خواهیم داشت:

$$\forall (x,y) , (x',y') \in F\;; \;\;y\neq y' \rightarrow x\neq x'$$

در نتیجه مشخص می‌شود که معادله دایره یا رابطه $$x^2+y^2=r^2$$ یک تابع نیست، زیرا برای مثال دارای دو عضو (2,2) و (2-,2) است که دارای مولفه‌های اول یکسان ولی با مقادیر متفاوت برای مولفه‌های دوم است. براساس تعریف عکس نقیض گزاره شرطی نیز چون مولفه‌های دوم با یکدیگر برابر نیستند باید نتیجه بگیریم که مولفه‌های اول نیز نابرابر هستند. ولی با توجه به این دو عضو، مشخص می‌شود که مولفه‌های اول یکسان هستند، پس این رابطه، تابع نخواهد بود.

در مقابل رابطه $$x^2+4=y$$ یک تابع است. این مسئله را در ادامه مورد بررسی قرار می‌دهیم. فرض کنید که $$x$$ و $$x'$$ دو مقدار باشند که با یکدیگر برابرند. بنابراین می‌توان نتیجه گرفت که مربع آن‌ها هم با هم برابر است. در نتیجه داریم:

$$x=x' \rightarrow x^2=x'^2$$

اگر به دو طرف این تساوی مقدار 4 را اضافه کنیم، تساوی تغییری نخواهد کرد. پس می‌توان نوشت:

$$x^2+4=x'^2+4\rightarrow y=y'$$

همانطور که دیده شد طبق تعریف اول نشان دادیم که رابطه $$x^2+4=y$$ یک تابع است زیر دارای هیج دو عضو با مولفه اول یکسان نیست.

بر این اساس می‌توان به یک قاعده برای بررسی رابطه و توابع رسید. معمولا زمانی که می‌خواهیم نشان دهیم که یک رابطه، نمی‌تواند تابع باشد از مثال نقض و تعریف دوم استفاده می‌کنیم ولی اگر لازم است که نشان دهیم یک رابطه، تابع نیز هست از تعریف اول برای اثبات کمک می‌گیریم. با این توضیحات به راحتی می‌توان نشان داد که چندجمله‌ای‌ها همگی تابع هستند. همچنین می‌توان با استفاده از ترکیب توابع، توابع جدید ایجاد کرد. البته در این حالت باید به دامنه و برد توابعی که در ترکیب به کار رفته‌اند توجه بیشتری داشت.

انواع توابع

می‌توان براساس خصوصیاتی که توابع دارند، آن‌ها را گروه‌بندی کرد. توابع ممکن است صعودی یا نزولی باشند که در حالت کلی آن‌ها را «یکنوا» (Monotone) می‌نامند. همچنین به عنوان یک دسته‌بندی دیگر می‌توان توابع را به دو گروه توابع «محدب» (Convex) و «مقعر» (Concave) طبقه‌بندی کرد. تعیین صعودی یا نزولی بودن و همینطور محدب یا مقعر بودن تابع به کمک مشتق تابع و تعیین علامت آن مشخص می‌شود. براساس یک طبقه‌بندی دیگر توابع با توجه به دامنه و برد می‌توان آن ها را به دو گروه توابع حقیقی و مختلط تقسیم کرد. منظور از توابع حقیقی، توابعی است که دامنه و برد آن‌ها، مجموعه اعداد حقیقی هستند. در مقابل دامنه و برد توابع مختلط مجموعه اعداد مختلط است.

برای آشنایی بیشتر با تابع می‌توانید به مطلب مفاهیم تابع – به زبان ساده و برای آگاهی از مفهوم برد و دامنه تابع نیز به مطلب دامنه و برد تابع — به زبان ساده مراجعه کنید. همچنین به منظور آگاهی از انواع تابع، مطالعه تابع یک به یک و پوشا — به زبان ساده نیز خالی از لطف نیست.

در صورت علاقه‌مندی به مباحث مرتبط در مورد ریاضیات، آموزش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• آموزش ریاضیات عمومی 1
• ماکزیمم و مینیمم تابع — به زبان ساده
• توابع چند متغیره — به زبان ساده
• مجانب تابع — به زبان ساده
• معکوس تابع و تابع معکوس — به زبان ساده

^^