تحلیل تیرها در بارگذاری محوری و خمشی – به همراه مثال

در مباحث «تحلیل تنش‌های برشی در تیرهای مستطیلی»، «تحلیل تنش‌های برشی در تیرهای دایره‌ای»، «تحلیل تنش‌های برشی در تیرهای بال پهن» و «تحلیل تیرهای مرکب و جریان برش درون آن‌ها»، به بررسی وضعیت تنش‌های برشی و نحوه تعیین این تنش‌ها در تیرهای مختلف پرداختیم. در این مقاله، تنش‌های ناشی از اعمال همزمان بارهای محوری و خمشی بر روی تیرها را مورد ارزیابی قرار خواهیم داد. در انتها نیز به منظور آشنایی بهتر با نحوه به کارگیری روابط ارائه شده، یک مثال کاربردی را تشریح خواهیم کرد.

اعمال همزمان بارهای محوری و خمشی

عضوهای ساختاری اغلب تحت تأثیر همزمان بارهای خمشی و بارهای محوری قرار می‌گیرند. این شرایط معمولاً در تحلیل قاب‌های بدنه هواپیما، ستون‌های ساختمان، ماشین‌های صنعتی، قطعات کشتی و فضاپیماها قابل مشاهده است. اگر ضخامت عضوهای تحت بارگذاری خیلی کم نباشد، امکان محاسبه تنش‌های ترکیبی با استفاده از برهم‌نهی تنش‌های خمشی و محوری وجود خواهد داشت.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

به منظور آشنایی با نحوه روند تحلیل شرایط مذکور، تیر یکسر گیردار زیر را در نظر بگیرید. تنها بار موجود بر روی تیر، بار مورب P است که به مرکز هندسی آخرین سطح مقطع اعمال می‌شود. این بار را می‌توان به دو مؤلفه (یک بار جانبی Q و یک بار محوری S) تجزیه کرد.

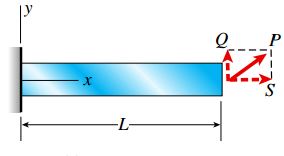
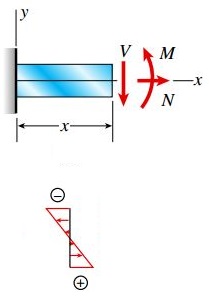
مؤلفه‌های بار جانبی و محوری، برآیندهای تنش متشکل از گشتاورهای خمشی M، نیروهای برشی V و نیروهای محوری N را همانند شکل زیر درون تیر به وجود می‌آورند.

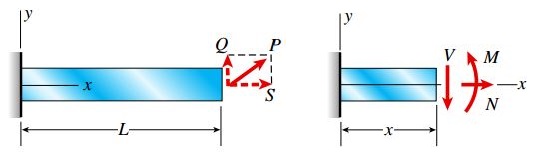
در سطح مقطعی با فاصله x از تکیه‌گاه، برآیندهای تنش به صورت زیر قابل محاسبه خواهند بود:

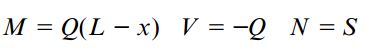
با به کارگیری رابطه‌های مناسب نیز می‌توان تنش‌های مربوط به هر یک از برآیندهای تنش را تعیین کرد (σ=-My/I ،τ=VQ/Ib ،σ=N/A). از آنجایی که نیروی محوری N و گشتاور خمشی M باعث ایجاد تنش‌های نرمال می‌شوند، با ترکیب این تنش‌های می‌توان توزیع تنش نهایی را به دست آورد. اگر تنها اثر اعمال نیروی محوری N را در نظر بگیریم؛ یک توزیع تنش یکنواخت با میانگین σ=N/A و مشابه شکل زیر بر روی تمام سطح مقطع تیر به وجود می‌آید. در این مثال بخصوص، تنش σ از نوع کششی بوده و نوع آن با علامت مثبت بر روی شکل نمایش داده شده است.

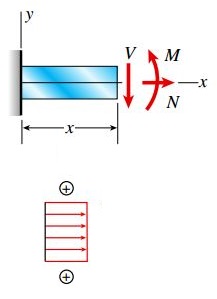
در اثر اعمال گشتاور خمشی نیز یک توزیع تنش خطی با رابطه σ=-My/I و به شکل زیر بر روی سطح مقطع تیر ایجاد می‌شود. قسمت بالایی تیر تحت فشار و قسمت پایینی آن در معرض کشش قرار می‌گیرد. فاصله y نسبت به محور z (درون مرکز هندسی سطح مقطع عرضی تیر) اندازه‌گیری می‌شود.

توزیع نهایی تنش‌های نرمال از برهم‌نهی تنش‌های ناشی از نیروی محوری و گشتاور خمشی به دست می‌آید. بنابراین، معادله تنش‌های ترکیبی به صورت زیر خواهد بود:

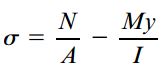
توجه داشته باشید که علامت N به کششی یا فشاری بودن تنش‌های به وجود آمده بستگی دارد (علامت مثبت برای تنش‌های کششی و علامت منفی برای تنش‌های فشاری در نظر گرفته می‌شود). علامت M نیز بر اساس قواعد علامت‌گذاری گشتاور خمشی به دست می‌آید (گشتاور خمشی مثبت باعث ایجاد فشار در بخش بالایی تیر و کشش در بخش پایینی آن می‌شود). علاوه بر این، علامت محور y در جهت رو به بالا مثبت است. اگر از این قواعد علامت‌گذاری برای رابطه تنش‌های ترکیبی استفاده کنیم، علامت تنش نرمال σ برای کشش، مثبت و برای فشار، منفی خواهد بود.

توزیع نهایی تنش به نسبت جبری بین مقادیر هر یک از پارامترهای مرتبط بستگی دارد. برای مثال مورد تحلیل در این مقاله می‌توان سه احتمال متفاوت را مطابق شکل زیر در نظر گرفت. اگر تنش خمشی موجود در بالای تیر (شکل بالا چپ) از نظر عددی کمتر از تنش محوری (شکل بالا راست) باشد، نحوه توزیع تنش بر روی مقطع سطح مقطع عرضی مطابق شکل پایین چپ خواهد بود. در صورت برابر بودن مقدار عددی تنش خمشی موجود در بخش بالایی تیر نسبت به تنش محوری، توزیع نهایی تنش به شکل یک مثلث درمی‌آید (شکل پایین وسط). حالت سوم زمانی رخ می‌دهد که مقدار عددی تنش خمشی بیشتر از تنش محوری باشد. در این حالت همانند شکل پایین راست، بخشی از سطح مقطع در معرض فشار و بخش دیگر در معرض کشش قرار می‌گیرد. توجه داشته باشید که فشاری بودن نیروی محوری یا معکوس بودن گشتاور خمشی باعث تغییر نسبی توزیع تنش می‌شود.

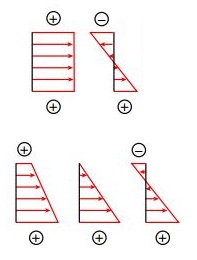
هرگاه بارهای خمشی و محوری به صورت همزمان بر روی یک سازه اعمال شوند، محور خنثی (خطی بر روی مقطع عرضی با تنش نرمال صفر) از مرکز هندسی سطح مقطع عبور نخواهد کرد. در شکل بالا نیز می‌توان مشاهده کرد که محور خنثی در هر یک از مثال‌ها با یکدیگر تفاوت دارد. این محور برای حالت اول خارج از مقطع عرضی، برای حالت دوم در گوشه مقطع و برای حالت سوم درون مقطع قرار گرفته است. در مثال انتهای این مقاله، نحوه به کارگیری این نکات را به منظور تعیین تنش‌های موجود در یک تیر تحت بارهای محوری را به طور کامل تشریح خواهیم کرد.

بارهای محوری خارج از مرکز

«بار محوری خارج از مرکز» (Eccentric Axial Load)، باری است که خط اثر آن از روی مرکز هندسی سطح مقطع عبور نمی‌کند.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

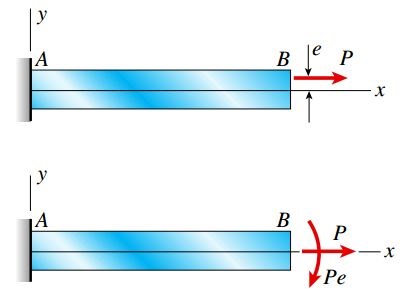
شکل زیر، نمونه‌ای از اعمال یک بار محوری خارج از مرکز بر یک تیر یکسر گیردار را نمایش می‌دهد (بار کششی P در فاصله e از محور خنثی x بر روی تیر AB اعمال شده است).

از نظر استاتیکی می‌توان بار خارج از مرکز P معادلِ یک نیروی محوری اعمال شده در راستای محور x (نیروی P) و یک گشتاور خمشی اعمال شده حول محور z در نظر گرفت (گشتاور Pe). توجه داشته باشید که گشتاور خمشی Pe (در شکل زیر) دارای علامت منفی است.

در شکل زیر، نمای سطح مقطع تیر از رو به رو (عمود بر محور خنثی) نمایش داده شده است. این نما، محورهای y و z گذرنده از مرکز هندسی C را نشان می‌دهد. بار خارج از مرکز P، با محور y (یکی از محورهای تقارن تیر) تقاطع دارد.

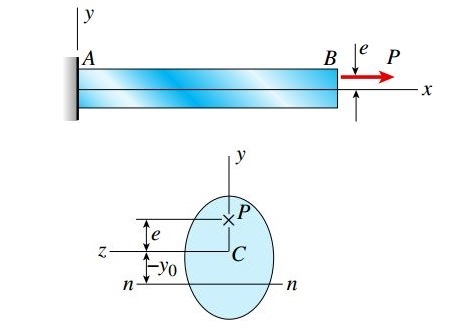
از آنجایی که نیروی محوری N بر روی تمامی مقاطع عرضی با P و گشتاور خمشی با Pe- برابر است، تنش نرمال بر روی هر نقطه دلخواه درون سطح مقطع از رابطه زیر به دست می‌آید:

A: مساحت سطح مقطع؛ I: ممان اینرسی حول محور z

در شکل زیر، توزیع تنش به دست آمده از رابطه بالا نمایش داده شده است. این شکل، برای شرایطی صدق می‌کند که P و e دارای علامت مثبت باشند.

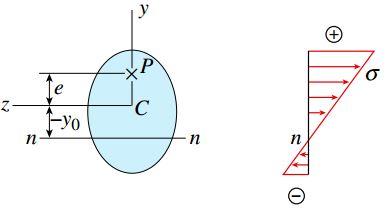
اگر تنش σ در رابطه بالا را برابر با صفر قرار دهیم و معادله به دست آمده را بر حسب مختصات y حل کنیم، محل قرارگیری محور خنثی nn به دست می‌آید (برای حالتی که P و e مثبت باشند). به این ترتیب، خواهیم داشت:

برای تعیین مختصات y₀، فاصله بین محور z (محور خنثی تحت خمش خالص) تا خط nn با تنش صفر (محور خنثی تحت بارگذاری ترکیبی محوری و خمشی) مورد اندازه‌گیری قرار می‌گیرد. به دلیل مثبت بودن y₀ در راستای محور y، جهت‌گیری آن به سمت پایین با y_0- نمایش داده می‌شود. با توجه به رابطه بالا، به خاطر داشته باشید که برای e مثبت، محور خنثی پایین‌تر از محور z و برای e منفی، محور خنثی بالاتر از محور z قرار می‌گیرد. در صورت کاهش میزان خروج از مرکز، فاصله y₀ افزایش می‌یابد و محور خنثی از مرکز هندسی دور خواهد شد. با نزدیک‌تر شدن مقدار e به صفر، محل اعمال بار به سمت مرکز هندسی، محور خنثی به فاصله بی‌نهایت و توزیع تنش به سمت یکنواخت شدن میل می‌کند. در طرف مقابل، افزایش میزان خروج از مرکز باعث کاهش فاصله y₀ و نزدیک شدن محور خنثی به مرکز هندسی می‌شود. هنگامی که e به یک مقدار بسیار بزرگ می‌رسد، محل اعمال بار در فاصله بی‌نهایت قرار گرفته، محور خنثی به مرکز هندسی نزدیک شده و توزیع تنش به شکل توزیع تنش در خمش خالص درمی‌آید.

نکات تکمیلی

معرفی تحلیل تیرهای تحت بارهای محوری در این مقاله، با فرض محاسبه گشتاورهای خمشی بدون در نظر گرفتن اعوجاج‌های تیر صورت گرفت. به عبارت دیگر، هنگام تعیین گشتاور خمشی M برای به کارگیری در رابطه تنش‌های ترکیبی باید امکان استفاده از ابعاد اولیه تیر (پیش از رخ دادن هرگونه تغییر شکل یا اعوجاج) فراهم باشد. این شرایط برای تیرهایی فراهم است که در هنگام اعمال خمش، سختی نسبتاً بالایی از خود نشان می‌دهند؛ چراکه در این حالت، میزان تغییر شکل و اعوجاج‌ها بسیار کوچک خواهد بود.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

نکته مهم در هنگام تحلیل یک تیر تحت بارهای محوری، ایجاد تمایز بین یک تیر ضخیم (نسبتاً کوتاه و مقاوم در برابر خمش) و یک تیر باریک (طول زیاد و انعطاف‌پذیری بسیار بالا) است. برای یک تیر ضخیم و کوتاه، اعوجاج‌های جانبی به قدری کوچک هستند که هیچ تأثیر قابل توجهی بر روی خط اثر نیروهای محوری ندارند. در این حالت، گشتاورهای خمشی به اعوجاج بستگی نخواهد داشت و تنش‌های موجود با استفاده از روابط ارائه شده در این مقاله قابل محاسبه خواهد بود. برای یک تیر باریک و بلند، مقدار اعوجاج‌های جانبی هر چقدر هم کوچک باشد، برای تغییر قابل توجه خط اثر نیروهای محوری کافی است. در این حالت، یک گشتاور خمشی اضافی برابر با حاصل‌ضرب نیروی محوری در اعوجاج جانبی بر روی تمام مقاطع تیر ایجاد می‌شود. به عبارت دیگر، یک فعل و انفعال یا کوپلینگ بین اثرات محوری و اثرات خمشی به وجود می‌آید.

وجه تمایز بین یک تیر ضخیم و کوتاه با یک تیر باریک و بلند زیاد واضح و مشخص نیست. به طور کلی، تنها راه تشخیص اهمیت فعل و انفعال اثرات محوری و خمشی، تحلیل تیر با در نظر گرفتن و بدون در نظر گرفتن این مسئله و بررسی میزان اختلاف بین نتایج این دو حالت است. به عنوان یک راهنمای کاربردی به خاطر داشته باشید که اگر نسبت طول به ارتفاع تیر برابر یا کمتر از 10 بود، می‌توان آن را به عنوان یک تیر ضخیم در نظر گرفت. در ادامه به منظور آشنایی بهتر با نحوه تحلیل یک تیر تحت بار محوری، به تشریح کامل یک مثال کاربردی می‌پردازیم. تیر مورد تحلیل در این مثال به عنوان یک تیر ضخیم در نظر گرفته می‌شود.

مثال

شکل زیر، تیر لوله‌ای ABC با طول L=60in را نمایش می‌دهد که انتهای A و B در آن با اتصالات مفصلی نگهداری می‌شوند. وینچ برقی موجود در نقطه E، بار W را توسط یک کابل به پایین نقطه C اعمال می‌کند. این کابل از درون یک قرقره بدون اصطکاک عبور کرده است (نقطه D). فاصله مرکز قرقره تا محور طولی لوله برابر با d=5.5in و سطح مقطع لوله به شکل مربعی با ضلع خارجی b=6in، مساحت A=20in² و ممان اینرسی I=86.67in⁴ است.

فیلم آموزش مقاومت مصالح ۲ در فرادرس

کلیک کنید

• الف) تنش‌های کششی و فشاری ماکسیمم ناشی از بار W=300lb را محاسبه کنید.
• ب) اگر حداکثر مقدار مجاز برای تنش نرمال موجود در لوله برابر با 3500psi باشد، حداکثر مقدار مجاز برای بار W چقدر خواهد بود؟ (فرض کنید که کابل، قرقره و قلاب CD در برابر بار W_max به اندازه کافی مقاوم هستند.)

الف) محاسبه تنش کششی ماکسیمم و تنش فشاری ماکسیمم

به منظور اجرای تحلیل، ابتدا باید یک تصویر ایده‌ال از تیر و بار اعمال شده بر آن را رسم کنیم (شکل زیر). به دلیل مقاومت تکیه‌گاه A در برابر جابجایی‌های افقی و عمودی، این قسمت را به شکل یک تکیه‌گاه مفصلی و به دلیل عدم مقاومت تکیه‌گاه B در برابر جابجایی‌های افقی و مقاومت در برابر جابجایی‌های عمودی، این بخش به شکل یک تکیه‌گاه غلتکی رسم شده است.

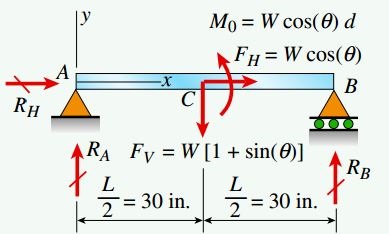
اگر به جای نیروهای کابل در نقطه D از نیروهای معادل F_H و F_V به همراه گشتاور M_O در نقطه C استفاده کنیم، خواهیم داشت:

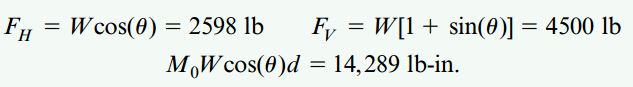
عکس‌العمل‌های تکیه‌گاهی تیر با علامت‌های R_A ،R_H و R_B نمایش داده شده‌اند. شکل زیر، نمودارهای نیروی محوری N، نیروی برشی V و گشتاور خمشی M را نشان می‌دهد. این کمیت‌ها با استفاده از نمودارهای جسم آزاد و معادلات تعادل به دست می‌آیند.

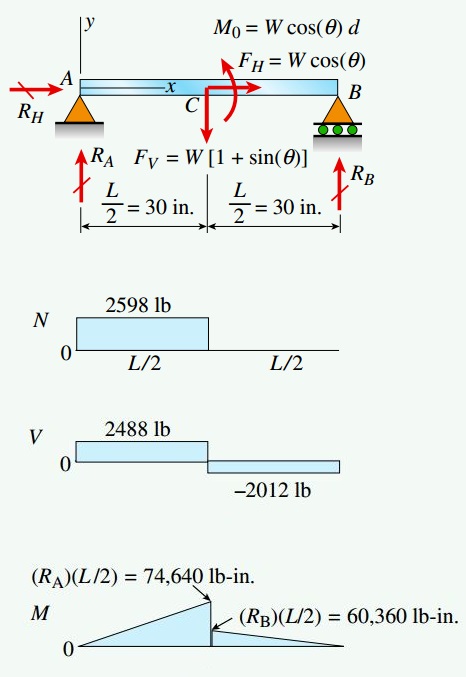
به این ترتیب، با به کارگیری معادلات استاتیکی تیر مورد تحلیل در این مثال، عکس‌العمل‌های تکیه‌گاهی تیر را به دست می‌آوریم:

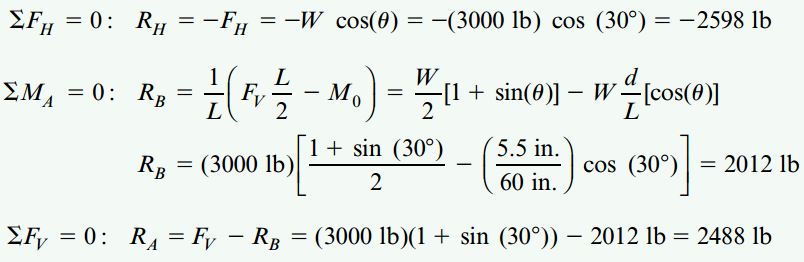
در مرحله بعد، با کمک نمودارهای نیروی محوری، نیروی برشی و گشتاور خمشی، تنش‌های ترکیبی موجود در تیر تعیین می‌کنیم.

تنش کششی ماکسیمم

تنش کششی ماکسیمم در مختصات y=-3in (پایین تیر و دقیقاً سمت چپ نقطه C) رخ می‌دهد. توجه داشته باشید که در این نقطه از تیر، تنش کششی ناشی از نیروی محوری به تنش کششی ناشی از بزرگ‌ترین گشتاور خمشی اضافه می‌شود. بنابراین:

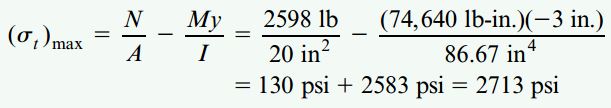
تنش فشاری ماکسیمم

تنش فشاری ماکسیمم در بالای تیر و دقیقاً سمت چپ نقطه C یا بالای تیر و سمت راست نقطه C (مختصات y=3in) رخ می‌دهد. میزیان تنش موجود در هر یک از این موقعیت‌ها به صورت زیر محاسبه می‌شود:

با توجه به مقادیر بالا، تنش فشاری ماکسیمم برابر است با:

در نتیجه، این تنش در بالای تیر و سمت چپ نقطه C رخ می‌دهد.

ب) حداکثر بار مجاز W

با توجه به فرض قسمت دوم این مثال، مقدار تنش نرمال مجاز برای تنش کششی در پایین تیر و دقیقاً سمت چپ نقطه C (تنش 2713psi برای بار W=3000lb) به مقدار σ_a=3500psi میل می‌کند. اگر از روابط ارائه شده برای تعیین عکس‌العمل‌های تکیه‌گاهی استفاده کنیم، نیروی محوری کششی در بخش AC و گشتاور مثبت در سمت چپ نقطه C به صورت زیر تعیین خواهند شد:

با توجه به رابطه معرفی شده برای تعیین تنش‌های ترکیبی، داریم:

با جایگذاری W_max به جای W و حل معادله بر اساس W_max خواهیم داشت:

در این مثال، با نحوه تعیین تنش‌های نرمال موجود در یک تیر تحت بارگذاری محوری و خمشی آشنا شدیم. به منظور محاسبه جداگانه تنش‌های برشی اعمال شده بر روی مقاطع عرضی تیر با استفاده از تنش‌های نرمال به دست آمده می‌توان از روابط معرفی شده در مباحث «تحلیل تنش‌های برشی در تیرهای مستطیلی»، «تحلیل تنش‌های برشی در تیرهای دایره‌ای»، «تحلیل تنش‌های برشی در تیرهای بال پهن» و «تحلیل تیرهای مرکب و جریان برش درون آن‌ها» استفاده کرد.

^^