تغییر طول عضوهای تحت بار محوری – آموزش جامع
به عضوهایی که تنها تحت کشش یا فشار قرار داشته باشند، «عضوهای تحت بار محوری» (Axially Loaded Members) گفته میشود. میلههای مستقیم از متداولترین عضوهای تحت بار محوری به شمار میروند. علاوه بر این، فنرها و کابلهای موجود در سازههای مختلف نیز با هدف قرارگیری در شرایط بارگذاری محوری مورد استفاده قرار میگیرند. در این مقاله، تغییر طول ناشی از اعمال بارهای محوری در فنرها، میلههای منشوری و کابلها را مورد بررسی قرار خواهیم داد. در انتها نیز به منظور آشنایی بیشتر با نحوه به کارگیری روابط ارائه شده، دو مثال کاربردی را به طور کامل تشریح خواهیم کرد.


فنر
اکثر طراحان به منظور محاسبه تغییر طول اجزای تشکیلدهنده سازههای تحت بار محوری، معمولاً محاسبات خود را از فنرهای مارپیچی شروع میکنند. این فنرها کاربرد بسیار گستردهای در ماشینها و دستگاههای مختلف دارند. به عنوان مثال، در ساخت هر خودرو از دهها فنر مارپیچی استفاده میشود. شکل زیر، نمونهای از یک فنر مارپیچی تحت شرایط بارگذاری محوری را نمایش میدهد.
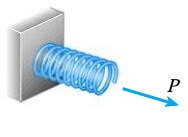
یک فنر مارپیچی که تحت بار محوری P قرار گرفته است.
هنگامی که یک بار در راستای محور فنر اعمال میشود، طول فنر همجهت با راستای اعمال بار افزایش یا کاهش مییابد. در صورت اعمال بار به سمت بیرون فنر (مانند شکل بالا)، طول فنر افزایش خواهد یافت. در این شرایط گفته میشود که فنر تحت «کشش» (Tension) قرار دارد. اگر بار به سمت داخل فنر اعمال شود، طول فنر کاهش خواهد یافت. در این شرایط گفته میشود که فنر تحت «فشار» (Compression) قرار دارد.
این تعریف به معنای وجود تنشهای کششی یا فشاری درون هر یک از حلقههای فنر نیست و هر یک از این حلقهها در ابتدای بارگذاری با برش مستقیم و پیچش مواجه میشود. با این وجود، نحوه کاهش یا افزایش طول یک فنر را میتوان معادلِ رفتار یک میله تحت کشش یا فشار در نظر گرفت. به همین دلیل، اصطلاحات مورد استفاده برای تحلیل فنر و میله مشابه یکدیگر هستند. شکل زیر، وضعیت یک فنر قبل و بعد از تغییر طول را نمایش میدهد. طول اولیه این فنر L است و با اعمال نیروی کششی P، این طول به اندازه δ افزایش مییابد (L+δ).
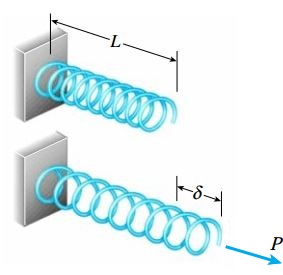
اگر رفتار فنر به صورت الاستیک خطی باشد، میزان تغییر طول آن با میزان بار اعمال شده متناسب خواهد بود:

k و f: ثابتهای تناسب
ثابت k با عنوان «سختی» (Stiffness) فنر شناخته میشود. این ثابت، نیروی مورد نیاز برای ایجاد یک واحد تغییر طول را نمایش میدهد (k=P/δ). ثابت f نیز با عنوان «انعطافپذیری» (Flexibility) فنر شناخته میشود. این ثابت، بیانگر تغییر طول ناشی از یک واحد نیرو است (f=δ/P). توجه داشته باشید که میتوان این روابط را برای شرایط بارگذاری فشاری نیز استفاده کرد. با توجه به تعریف سختی و انعطافپذیری، این دو کمیت معکوس یکدیگر هستند:
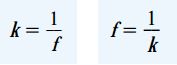
با اعمال یک بارِ مشخص و اندازهگیری میزان تغییر طول ناشی از آن، انعطافپذیری فنر به راحتی محاسبه میشود. به این ترتیب، سختی فنر نیز با استفاده از رابطه بالا به دست میآید. سختی و انعطافپذیری به ترتیب با عناوین «ثابت فنر» (Spring Constant) و «انطباق» (Compliance) نیز شناخته میشوند. خواص به دست آمده از روابط بالا در تحلیل و طراحی بسیاری از دستگاههای مکانیکی دارای فنر کاربرد دارد.
میله منشوری
بر اثر اعمال بارهای کششی یا فشاری بر روی میلهها، طول آنها افزایش یا کاهش مییابد.
به منظور تحلیل این رفتار، میله منشوری نمایش داده شده در شکل زیر را در نظر بگیرید. میله منشوری عضوی با محور طولی مستقیم و سطح مقطع ثابت است.
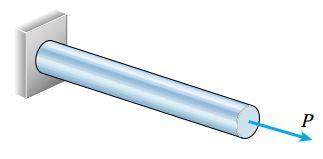
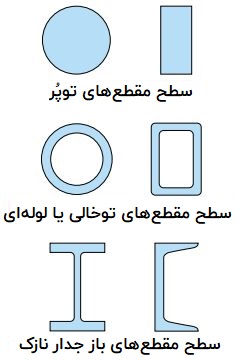
در اکثر منابع، به منظور نمایش میلههای منشوری از مقطع دایرهای استفاده میشود. با این وجود، میلههای مورد استفاده در سازههای مختلف میتوانند اشکال متنوعی داشته باشند.
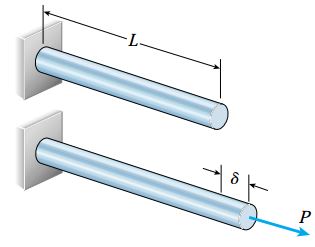
شکل زیر، تغییر طول δ یک میله منشوری در هنگام اعمال بار کششی P را نمایش میدهد. اگر راستای اعمال بار از مرکز هندسی سطح مقطع انتهای میله عبور کند، توزیع تنش درون میله یکنواخت خواهد بود. به این ترتیب میتوان تنش نرمال در مقاطع دیگر را با استفاده از رابطه σ =P/A محاسبه کرد. A، مساحت سطح مقطع میله است. علاوه بر این، در صورت همگن بودن ماده تشکیلدهنده میله، میزان کرنش محوری نیز از رابطه ε=δ/L به دست میآید. کمیتهای δ و L، به ترتیب تغییر طول ایجادشده و طول اولیه میله را نمایش میدهند.
اگر ماده تشکیلدهنده میله از قانون هوک پیروی کند (ماده الاستیک خطی)، رابطه بین تنش و کرنش طولی از طریق σ=Eε بیان میشود. E، مدول الاستیسیته ماده را نمایش میدهد. با ادغام این رابطه با ε=δ/L و σ =P/A، معادله زیر برای محاسبه میزان تغییر طول میله به دست میآید:
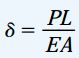
بر اساس این رابطه، تغییر طول با میزان بار اعمال شده و طول اولیه میله رابطه مستقیم و با مدول الاستیسیته و مساحت سطح مقطع رابطه عکس دارد. حاصلضرب EA با عنوان «صلبیت محوری» (Axial Rigidity) میله شناخته میشود. رابطه بالا برای شرایط بارگذاری فشاری نیز قابل استفاده است. افزایش یا کاهش طول یک عضو معمولاً به وسیله بازرسی آن مشخص میشود.
با این وجود، در برخی از موارد (نظیر تحلیل یک میله نامعین استاتیکی)، مشخص کردن نوع تغییر طول میله با استفاده از قواعد علامتگذاری صورت میگیرد. بر اساس این قواعد، علامت مثبت برای افزایش طول و علامت منفی برای کاهش طول در نظر گرفته میشود.
در اکثر مواقع، میزان تغییر طول میله (δ) در مقایسه با طول اولیه آن (L) بسیار کوچک است؛ مخصوصاً اگر ماده تشکیلدهنده میله از جنس فولاد یا آلومینیوم باشد. به عنوان مثال، اگر یک سازه آلومینیومی با طول 75 اینچ (in) و مدول الاستیسیته 10500 کیلو پوند بر اینچ مربع (ksi)، در معرض یک تنش فشاری با مقدار 7000 پوند بر اینچ مربع (psi) قرار گرفته باشد، طول سازه به اندازه 0.05 اینچ کوتاهتر میشود (δ). به این ترتیب، نسبت تغییر طول به طول اولیه برابر با 0.05/75 یا 1/1500 خواهد بود (ε). در نتیجه، طول نهایی میله 0.999 برابر طول اولیه آن است. در صورت کوچک بودن میزان تغییر طول میتوان به جای طول نهایی از طول اولیه در محاسبات استفاده کرد.
سختی و انعطافپذیری یک میله منشوری با استفاده از روابطی مشابه با روابط معرفی شده برای ثابتهای فنر تعیین میشوند. سختی، نیروی مورد نیاز برای ایجاد یک واحد تغییر طول و انعطافپذیری، تغییر طول ناشی از یک واحد نیرو است. به این ترتیب، برای یک میله منشوری داریم:
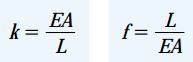
مقادیر سختی و انعطافپذیری عضوها، نقش ویژهای در تحلیل سازهها با استفاده از روشهای کامپیوتری دارند.
کابل
کابلها برای انتقال نیروهای کششی بزرگ در هنگام بلند کردن یا کشیدن اشیا سنگین، بالا بردن آسانسورها، مهار کردن دکلها و نگهداری پلهای معلق مورد استفاده قرار میگیرند. این عضوها نمیتوانند همانند فنرها و میلههای منشوری در برابر نیروهای فشاری مقاومت کنند. علاوه بر این، مقاومت آنها در برابر خمش نیز بسیار کم است. با این وجود، کابلها به عنوان عضوهای تحت بار محوری در نظر گرفته میشوند؛ چراکه این عضوها تنها در معرض نیروهای کششی قرار میگیرند. نیروهای کششی درون کابلها در راستای محور آنها اعمال میشوند. به همین دلیل، امکان تغییر مقدار و جهتگیری این نیروها با توجه به پیکربندی کابل وجود دارد.
کابلها از تعداد زیادی سیم تشکیل میشوند که به طرز خاصی در کنار یکدیگر قرار گرفتهاند. نحوه قرارگیری این سیمها در کنار یکدیگر به کاربری کابل بستگی دارد. در شکل زیر میتوان آرایش معمول برای کابلهای فولادی را مشاهده کرد. کابل نمایش داده شده در این شکل از 6 رشته سیم تشکیل شده است. این رشتهها به صورت مارپیچی در اطراف یک رشته مرکزی بافته شدهاند. هر رشته نیز تعداد زیادی سیم با آرایش مارپیچی را دربرمیگیرد. به همین دلیل، کابلها معمولاً با عنوان «طناب سیمی» (Wire Rope) نیز خطاب میشوند.

«مساحت مؤثر» (Effective Area) یا «مساحت فلزی» (Metallic Area) سطح مقطع کابل با جمع مساحت سطح مقطعهای تمام سیمها برابر است. به دلیل وجود فضاهای خالی بین هر یک از سیمها، مساحت مؤثر سطح مقطع کابل از مساحت دایره دربرگیرنده تمام رشتهها کمتر خواهد بود. به عنوان مثال، مساحت واقعی سطح مقطع کابل 1 اینچی، تنها 0.471 اینچ مربع است؛ در صورتی که مساحت دایرهای با قطر 1 اینچ، 0.785 اینچ مربع خواهد بود.
در صورت یکسان بودن بار کششی، ماده تشکیلدهنده و مساحت مؤثر سطح مقطع، میزان افزایش طول یک کابل بیشتر از افزایش طول یک میله خواهد بود. دلیل این موضوع، شباهت بین نحوه قرارگیری سیمها در کابل با نحوه قرارگیری الیاف درون یک طناب است. این آرایش باعث کاهش مدول الاستیسیته کابل (مدول مؤثر) نسبت به مدول الاستیسیته ماده تشکیلدهنده آن میشود. به عنوان مثال، مدول مؤثر کابلهای فولادی در حدود 140 گیگا پاسکال (20000 کیلو پوند بر اینچ مربع) و مدول فولاد در حدود 210 گیگا پاسکال (30000 کیلو پوند بر اینچ مربع) است. به منظور محاسبه میزان تغییر طول کابل باید از مدول مؤثر به جای پارامتر E و از مساحت مؤثر به جای پارامتر A در رابطه زیر استفاده کرد:
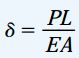
در مسائل کاربردی، اطلاعات مربوط به ابعاد سطح مقطع و دیگر خواص کابلها توسط تولیدکنندگان تعیین و ارائه میشوند. در جدول زیر، خصوصیات تقریبی برخی از کابلهای فولادی آورده شده است. توجه داشته باشید که ستون مربوط به بار نهایی، میزان بار مورد نیاز برای پاره شدن کابل را نمایش میدهد. با استفاده از بار نهایی در تعیین ضریب ایمنی، مقدار بار مجاز محاسبه میشود. ضریب ایمنی کابل با توجه به نوع کاربری آن در محدودهای بین 3 تا 10 قرار میگیرد. سیمهای به کار گرفته در یک کابل معمولاً از فولاد مقاوم ساخته میشوند. در برخی از مواقع، تنش کششی محاسبه شده در این سیمها هنگام اعمال بار شکست به 1400 مگا پاسکال میرسد.
| قطر اسمی بر حسب میلی متر (mm) | وزن تقریبی بر حسب نیوتن بر متر (N/m) | مساحت موثر بر حسب میلیمتر مربع (mm2) | بار نهایی بر حسب کیلونیوتن (kN) |
| 12 | 6.1 | 76.7 | 102 |
| 20 | 13.9 | 173 | 231 |
| 25 | 24.4 | 304 | 406 |
| 32 | 38.5 | 481 | 641 |
| 38 | 55.9 | 697 | 930 |
| 44 | 76.4 | 948 | 1260 |
| 50 | 99.8 | 1230 | 1650 |
مثالهای کاربردی
در این بخش، به منظور آشنایی با روشهای تحلیل فنر یا میلههای موجود در دستگاههای ساده، به تشریح کامل دو مثال کاربردی میپردازیم. نکته بسیار مهم برای حل این مسائل، نحوه استفاده از نمودار جسم آزاد، معادلات تعادل و معادلات تغییر طول است.
مثال 1
شکل زیر، قاب ABC متشکل از یک بازوی افقی به طول b=10.5in و یک بازوی عمودی به طول c=6.4 را نمایش میدهد. این قاب از طریق لولای B به قاب خارجی BCD متصل شده است. موقعیت نوک بازوی BC در نقطه C توسط فنری با سختی 4.2 پوند بر اینچ (lb/in) کنترل میشود. در کنار این فنر یک میله رزوه دار قرار دارد که محل قرارگیری آن به وسیله یک مهره آجدار تغییر میکند. گام رزوههای میله (فاصله بین دو شیار متوالی) برابر با 1/16 اینچ است. به این ترتیب، یک چرخش کامل مهره باعث حرکت میله به اندازه 1/16 اینچ خواهد شد. در ابتدا، هیچ وزنهای بر روی آویز وجود ندارد. در این وضعیت، مهره به اندازهای چرخانده میشود که نوک بازوی BC دقیقاً بالای علامت مرجع بر روی قاب بیرونی قرار گیرد.
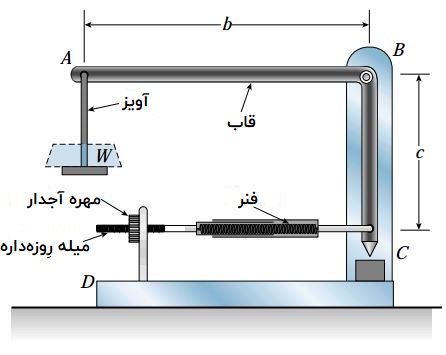
اگر یک وزنه 2 پوندی بر روی آویز قرار داده شود، نوک بازوی BC با چند چرخش کامل مهره به موقعیت اولیه خود بازمیگردد؟ (از تغییر شکل قطعات فلزی دستگاه چشمپوشی کنید.)
راه حل
با دقت بر روی شکل بالا متوجه خواهید شد که حرکت رو به پایین وزنه W باعث حرکت رو به راست نوک بازوی BC در نقطه C میشود. با حرکت نوک بازو به سمت راست، طول فنر افزایش مییابد. میزان افزایش طول فنر با تعیین مقدار نیروی درون فنر قابل محاسبه خواهد بود. به منظور تعیین این نیرو، باید نمودار جسم آزاد قاب ABC را مطابق شکل زیر رسم کنیم. در این نمودار، W، نیروی حاصل از وزنه روی آویز و F، نیروی درون فنر را نمایش میدهد. عکسالعملهای لولا در نقطه B، توسط پیکانهای خط خورده نمایش داده شدهاند.
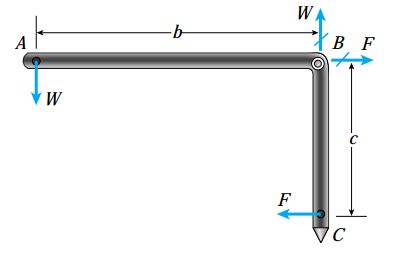
با در نظر گرفتن تعادل بین گشتاورها حول نقطه B، رابطه زیر به دست میآید:
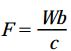
توجه: گشتاور حول یک نقطه، با ضرب نیرو در فاصله محاسبه میشود. به عنوان مثال، گشتاور حاصل از نیروی F حول نقطه B با حاصلضرب Fc و گشتاور حاصل از نیروی W حول نقطه B با حاصلضرب Wb برابر است.
تغییر طول ناشی از اعمال نیروی F بر روی فنر نیز به صورت زیر تعیین میشود:
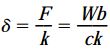
برای بازگرداندن نوک بازوی BC به موقعیت اولیه خود، باید مهره را به اندازهای بچرخانیم که مقدار حرکت میله با تغییر طول فنر برابر شود. اگر مقدار حرکت میله بر اثر چرخاندن مهر را p، تعداد دوران مهره را n و مقدار حرکت کلی میله را np در نظر بگیریم، رابطه زیر به دست میآید:
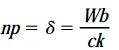
کمیت p، با عنوان گام رزوههای میله نیز شناخته میشود. با حل رابطه بالا نسبت به پارامتر n، رابطه زیر برای محاسبه تعداد چرخش مورد نیاز برای بازگرداندن نوک بازوی BC به موقعیت اولیه به دست میآید:
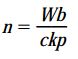
با جایگذاری مقادیر مربوط هر یک از پارامترها، خواهیم داشت:
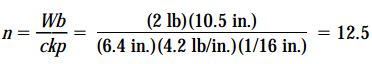
به این ترتیب، اگر مهره را 12.5 بار بچرخانیم، میله به اندازه تغییر طول فنر به سمت چپ حرکت میکند. در نتیجه، نوک بازوی BC به موقعیت اولیه خود بازمیگردد.
مثال 2
دستگاه نمایش داده شده در شکل زیر از یک تیر افقی (ABC) و دو میله نگهدارنده عمودی (BD و CE) تشکیل میشود. در بخش CE، هر دو انتهای میله به وسیله اتصالات مفصلی به نقاط C و E متصل شدهاند اما در بخش BD، یک انتهای میله به وسیله اتصالات مفصلی در نقطه B متصل و انتهای دیگر در نقطه D فیکس شده است.
فاصله نقطه A تا B برابر با 450 میلیمتر؛ فاصله نقطه B تا C برابر با 225 میلیمتر؛ طول BD برابر با 480 میلیمتر؛ طول CE برابر با 600 میلیمتر؛ مساحت سطح مقطع BD برابر با 1020 میلیمتر مربع؛ مساحت سطح مقطع CE برابر با 520 میلیمتر مربع؛ و مدول الاستیسیته میلهها برابر با 205 گیگا پاسکال است.
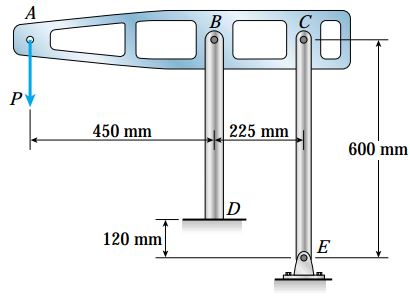
اگر حداکثر میزان جابجایی نقطه A بر اثر اعمال بارِ P برابر با 1 میلیمتر باشد، حداکثر بار مجاز (Pmax) چقدر خواهد بود؟ (با فرض صلب بودن تیر ABC)
راه حل
برای محاسبه میزان جابجایی نقطه A، در ابتدا باید جابجاییهای نقاط B و C را تعیین کنیم. بنابراین، با استفاده از رابطه کلی δ=PL/EA، تغییر طول میلههای BD و CE را به دست میآوریم. به این منظور، با رسم یک نمودار جسم آزاد (مطابق شکل زیر)، نیروهای موجود در این میلهها را مشخص میکنیم.
به دلیل وجود اتصالات مفصلی در هر دو انتهای میله CE، این میله به عنوان عضوی در نظر گرفته میشود که تنها نیروی عمودی FCE را به تیر افقی انتقال میدهد. از سوی دیگر، به دلیل ثابت بودن انتهای پایینی میله BD، این میله نیروی عمودی FBD و نیروی افقی H را به تیر اعمال میکند. با در نظر گرفتن شرایط تعادل برای تیر ABC در راستای افقی، نیروی افقی H حذف خواهد شد (زیرا هیچ نیروی افقی دیگری در نمودار جسم آزاد وجود ندارد).

با استفاده از معادلات تعادل میتوان نیروهای FBD و FCE را بر حسب بارِ P بیان کرد. به این منظور، در ابتدا گشتاورهای P و FBD را حول نقطه C را به دست میآوریم و آنها را برابر با یکدیگر قرار میدهیم. این کار را برای گشتاورهای P و FCE حول نقطه B نیز تکرار میکنیم. به این ترتیب، داریم:

توجه داشته باشید که نیروی FCE رو به پایین و نیروی FBD رو به بالا عمل میکند. بنابراین، عضو CE تحت کشش و عضو BD تحت فشار خواهد بود. میزان کاهش طول BD از رابطه زیر به دست میآید:
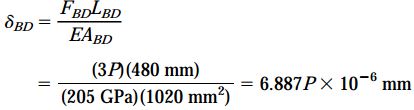
کاهش طول δBD بر حسب میلیمتر و بار P بر حسب نیوتن بیان میشود. مشابه رابطه بالا، میزان افزایش طول عضو CE را نیز به دست میآوریم:
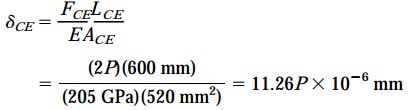
جابجایی δCE با واحد میلیمتر و P بار با واحد نیوتن بیان میشود. با مشخص شدن تغییر طول این دو میله میتوان میزان جابجایی نقطه A را نیز محاسبه کرد.
نمودار جابجایی
نمودار جابجایی و موقعیت نسبی نقاط B ،A و C در شکل زیر رسم شده است. خط ABC، موقعیت نسبی این سه نقطه پیش از بارگذاری را نمایش میدهد. پس از اعمال بارِ P، طول عضو BD به اندازه δBD کاهش مییابد و نقطه B به ‘B تغییر مکان میدهد. علاوه بر این، طول عضو CE نیز به اندازه δCE افزایش مییابد و نقطه C تا ‘C جابجا میشود. به دلیل فرض صلب بودن تیر ABC، مسیر گذرنده از نقاط ‘B‘ ،A و ‘C یک خط راست را تشکیل میدهد.
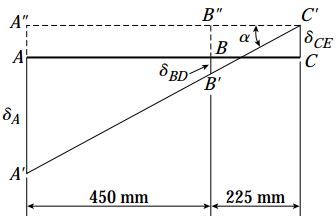
برای درک بهتر تغییر موقعیت نسبی نقاط نسبت به یکدیگر، جابجاییها با مقیاس چند برابر نمایش داده شدهاند. در واقعیت، خط ABC تحت یک زاویه بسیار کوچک دوران میکند و بر روی موقعیت جدید خود، یعنی خط ‘A’B’C قرار میگیرد. با استفاده از تشابه مثلثها میتوانیم روابط بین جابجاییهای نقاط B ،A و C را به دست آوریم. به ترتیب، با در نظر گرفتن تشابه مثلثهای ‘A’’A’C و ‘B’’B’C داریم:
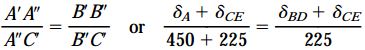
تمام عبارات بالا بر حسب میلیمتر هستند. با جایگذاری مقادیر δBD و δCE، خواهیم داشت:
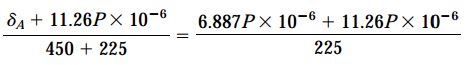
با توجه به اطلاعات مسئله، حد بالایی جابجایی نقطه A برابر با 1 میلیمتر در نظر گرفته شده است. به این ترتیب، با جایگذاری این مقدار در رابطه بالا و حل آن نسبت به پارامتر P به جواب زیر میرسیم:
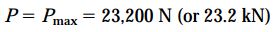
هنگامی که بار اعمال شده به Pmax برسد، جابجایی نقطه A برابر با 1 میلیمتر خواهد بود.
نکته اول
به دلیل رفتار الاستیک خطی سازه در این مسئله، جابجاییهای ایجاد شده با میزان بار اعمال شده متناسب هستند. به عنوان مثال، اگر بار اعمال شده نصف بار ماکسیمم (Pmax) باشد (P=11.6kN)، جابجایی رو به پایین نقطه A برابر با 0.5 میلیمتر خواهد بود.
نکته دوم
پیش از این مدعی شدیم که بر اثر اعمال بارِ P، خط ABC تحت یک زاویه بسیار کوچک دوران میکند. به همین دلیل، برای نمایش بهتر موقعیت نسبی نقاط پس از جابجایی باید نمودار جابجایی را با مقیاس چند برابر رسم کنیم. به منظور اثبات این موضوع، مقدار زاویه دوران خط ABC را با توجه به نمودار جابجایی زیر محاسبه میکنیم:

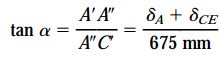
جابجایی نقطه A برابر با 1 میلیمتر و افزایش طول عضو CE برابر با 0.261 میلیمتر است (با جایگذاری Pmax در رابطه مربوط به δCE، افزایش طول عضو CE به دست میآید). به این ترتیب، داریم:
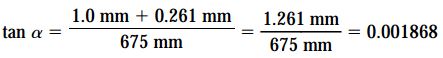
به این ترتیب، زاویه دوران α برابر با 0.11 درجه است. این زاویه به قدری کوچک است که در صورت رسم نمودار جابجایی با مقیاس واقعی، تفاوت بین خط ABC و ‘A’B’C قابل تشخیص نخواهد بود. از اینرو، در هنگام کار با نمودارهای جابجایی میتوانیم جابجاییها را به عنوان کمیتهای بسیار کوچک در نظر بگیریم و هندسه نمودار را سادهتر رسم کنیم. در مثال ارائه شده، فرض کردیم که نقاط B ،A و C تنها به صورت عمودی جابجا میشوند؛ در صورتی که اگر میزان جابجاییها بزرگ بودند، فرض میکردیم که این نقاط بر روی یک مسیر منحنیشکل جابجا میشوند.
^^













سلام. بسیار عالی و قابل فهم و تاثیر گذار میباشد