طراحی تیر در شرایط بارگذاری خمشی – با مثال های کاربردی
در فرآیند تحلیل یک تیر، عوامل زیادی نظیر نوع سازه (هواپیما، اتومبیل، پل، ساختمان و ...)، جنس مواد تشکیلدهنده، نوع بارهای اعمال شده، شرایط محیطی و هزینه ساخت سازه در نظر گرفته میشود. اگرچه، با در نظر گرفتن عامل مقاومت، شکل و اندازه تیر باید به گونهای باشد که تنشهای اعمال شده از میزان تنشهای مجاز ماده تشکیلدهنده آن عبور نکند. در این مقاله، به معرفی مبانی طراحی تیر در شرایط بارگذاری خمشی (بر اساس رابطه خمش) خواهیم پرداخت. در انتها نیز به منظور آشنایی با روابط و مفاهیم ارائه شده، چند مثال متنوع و کاربردی را تشریح خواهیم کرد.


مدول مقطع
به منظور طراحی تیرهای مقاوم در برابر تنشهای خمشی، در ابتدا باید «مدول مقطع» (Section Modulus) مورد نیاز را محاسبه کرد. به عنوان مثال، اگر سطح مقطع یک تیر دارای تقارن مضاعف و تنشهای مجاز برای بارگذاری کششی و فشاری یکسان باشند، مدول مقطع از تقسیم گشتاور خمشی ماکسیمم بر تنش خمشی مجاز به دست میآید:
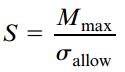
S: مدول مقطع؛ Mmax: گشتاور خمشی ماکسیمم؛ σallow: تنش مجاز
تنش مجاز با توجه به خصوصیات رفتاری ماده و ضریب ایمنی مورد نیاز تعیین میشود. برای اطمینان از قرارگیری تنشهای اعمال شده در محدودهای پایینتر از تنش مجاز، مقدار مدول مقطع باید حداقل به بزرگی مقدار به دست آمده از رابطه بالا باشد. اگر سطح مقطع تیر دارای تقارن مضاعف نباشد یا تنشهای مجاز برای بارگذاریهای کششی و فشاری با یکدیگر تفاوت داشته باشند، دو مدول مقطع محاسبه میشود (یکی برای بارگذاری کششی و دیگری برای بارگذاری فشاری). سپس، طراحی تیر به گونهای صورت میگیرد که پارامترهای دخیل، در هر دو مدول صدق کنند. برای به حداقل رساندن وزن و مواد به کار گرفته شده، تیر باید به گونهای طراحی شود که علیرغم فراهم کردن مدول مقطع مورد نیاز و دیگر الزامات طراحی، سطح مقطع آن دارای کمترین مساحت ممکن باشد.
تیرها با توجه به نیازهای مختلف در شکلها و اندازههای بسیار متنوعی ساخته میشوند. به عنوان مثال، تیرهای فولادی بسیار بزرگ (مانند نمونه نمایش داده شده در شکل زیر) با جوشکاری، تیرهای آلومینیومی با استفاده از قالب، تیرهای چوبی از طریق برش و تیرهای بتن مسلح نیز با کمک قالبهای مخصوص به شکلها و اندازههای مورد نیاز درمیآیند.

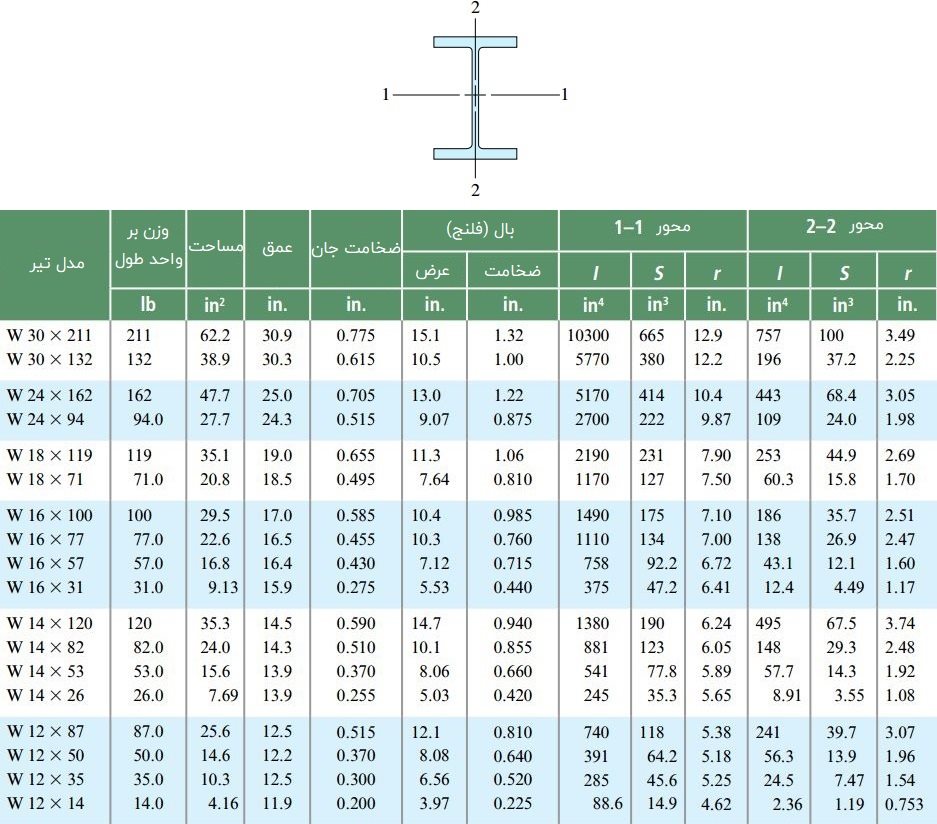
علاوه بر ساخت سفارشی این عضوهای سازهای، تیرهای فولادی، آلومینیومی، پلاستیکی و چوبی در شکلها و اندازههای استاندارد نیز تولید میشوند. از شکلهای استاندارد و پرکاربرد میتوان تیرهای «بال پهن» (Wide Flange)، تیرهای I شکل، نبشیها، کانالها، تیرهای مستطیلی و لولهها را نام برد. ابعاد و خواص بسیاری از انواع تیرهای استاندارد را میتوان در کتابها و دستورالعملهای مهندسی سازه پیدا کرد. به عنوان مثال در ایالات متحده، اندازه و شکل تیرهای ساخته شده از فولاد سازهای با توجه استانداردهای موسسهی آمریکایی ساخت و ساز فولاد (AISC) و بر اساس سیستم یکاهای آمریکایی و سیستم SI تعیین میشود. جدولهای موجود در این دستورالعملها، ابعاد سطح مقطع و خواصی نظیر وزن، مساحت مقطع، ممان اینرسی و مدول مقطع را نمایش میدهند.
کارایی نسبی شکلهای مختلف تیر
یکی از اهداف طراحی تیر، استفاده بهینه از مواد با توجه به عملکرد، ظاهر، هزینه ساخت و دیگر محدودیتها است. از نقطه نظر مقاومت، کارایی یک تیر در هنگام اعمال خمش در درجه اول به شکل سطح مقطع بستگی دارد. به طور کلی، هر چه درصد بیشتری از مواد سازنده یک تیر تا جای ممکن از محور خنثی فاصله داشته باشند، کارایی آن تیر افزایش مییابد.
با فاصله مواد از محور خنثی، مدول مقطع بزرگتر و مقاومت آن در برابر گشتاور خمشی بیشتر میشود (با در نظر گرفتن تنش مجاز ثابت). برای درک بهتر تأثیر شکل سطح مقطع بر روی کارایی نسبی تیر، شکل زیر را در نظر بگیرید. این شکل، یک سطح مقطع مستطیلی با عرض b و ارتفاع h را نمایش میدهد.
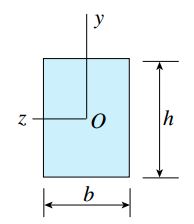
مدول مقطع سطح بالا به صورت زیر به تعیین میشود:
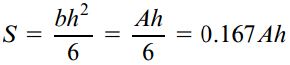
A: مساحت سطح مقطع
رابطه بالا نشان میدهد که یک سطح مقطع مستطیلی با مساحت مشخص، افزایش ارتفاع باعث بهبود کارایی تیر میشود (برای ثابت ماندن مساحت، عرض مقطع کاهش مییابد). با این وجود، مشخصاً یک محدودیت عملی در میزان افزایش ارتفاع تیر وجود دارد؛ چراکه در صورت افزایش بیش از حد نسبت ارتفاع به عرض سطح، پایداری جانبی تیر کاهش مییابد. از اینرو، یک تیر با سطح مقطع مستطیلی خیلی باریک، بیشتر به دلیل کمانش جانبی میشکند (نه به دلیل مقاومت کم). در ادامه، یک سطح مقطع دایرهای شکل به قطر d (شکل زیر) را با یک سطح مقطع مربعی با مساحت یکسان مقایسه میکنیم. ضلع مربع هم مساحت با دایره مورد بررسی h=(d/2)(π)0.5 است.
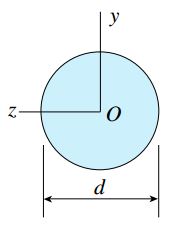
مدول مقطع سطح مربعی و دایرهای به ترتیب برابر است با:
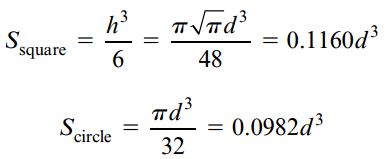
در نتیجه، نسبت این دو مدول به صورت زیر خواهد بود:
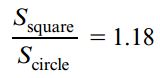
این نسبت نشان میدهد که در صورت برابر بودن مساحت سطح مقطع دو تیر، مقاومت خمش یک تیر دارای سطح مقطع مربعی نسبت به تیر دیگر با سطح مقطع دایرهای بیشتر است. در تیرهای دایرهای نقاط بیشتری در نزدیکی محور خنثی تیر قرار دارند. به این ترتیب، محدود کمتری در معرض تنشهای حداکثری قرار گرفته و مشارکت کمتری به منظور مقاومت در برابر بارگذاری خمشی صورت میگیرد. شکل ایدئال سطح مقطع یک تیر با مساحت A و ارتفاع h با قرار دادن نصف مساحت در فاصله h/2 بالای محور خنثی و نصف دیگر مساحت در فاصله h/2 پایین این محور قابل تعیین است (مانند شکل زیر).
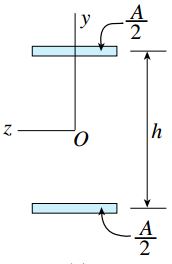
ممان اینرسی و مدول مقطع شکل ایدئال بالا به صورت زیر به دست میآید:
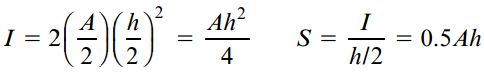
در مسائل واقعی، این محدودیتهای تئوری برای ساخت سطح مقطعهای بال پهن و I شکل تقریباً رعایت میشود (شکل زیر).
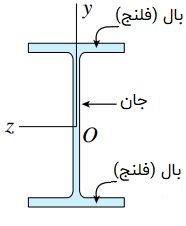
مقدار تقریبی مدول مقطع تیرهای بال پهن استاندارد برابر است با:
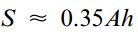
این مدول از مقدار ایدئال کمتر است اما از مدول مقطع یک سطح مستطیلی (با مساحت و ارتفاع مشابه) فاصله زیادی دارد. عرض بزرگ تیر بال پهن را میتوان به عنوان یکی دیگر از ویژگیهای مطلوب آن در نظر گرفت. این ویژگی باعث افزایش پایداری تیر در برابر کمانش جانبی میشود (نسبت به یک تیر مستطیلی با ارتفاع و مدول یکسان). از طرف دیگر، میزان نازک بودن جانِ تیرهای بال پهن دارای محدودیتهای اجرایی است. طراحی یک جانِ بسیار نازک، احتمال رخ دادن کمانش محلی یا افزایش موضعی تنش برشی را بیشتر میکند.
مثالهای کاربردی
در این بخش، به منظور آشنایی با نحوه انتخاب ابعاد یک تیر بر اساس تنشهای مجاز، به تشریح چهار مثال متنوع و کاربردی میپردازیم. در این مثالها، تنها اثرات تنشهای خمشی به دست آمده از رابطه خمش را مورد ارزیابی قرار میدهیم.
مثال 1
شکل زیر، یک تیر ساده با طول L=12ft را نمایش میدهد که تحت یک بار گسترده یکنواخت با شدت q=420lb/ft قرار دارد. مقدار مجاز تنش خمشی برابر با 1800psi، وزن مخصوص چوب برابر با 35lb/ft3 و صفحات جانبی تیر در برابر کمانش و واژگونی مقاوم است. با توجه به اطلاعات مسئله، اندازه مناسب تیر را بر اساس جدول ارائه شده تعیین کنید.
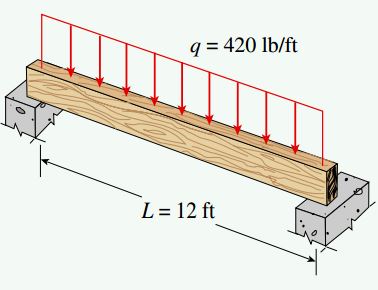
به منظور تحلیل بهتر این مسئله باید مراحل زیر را دنبال کنیم:
- محاسبه مدول مقطع مورد نیاز بر اساس میزان بار اعمال شده
- تعیین یک اندازه آزمایشی برای تیر
- اضافه کردن وزن تیر به بار اعمال شده و محاسبه مدول مقطع جدید
- بررسی صحت اندازه انتخاب شده
- انتخاب یک تیر بزرگتر در صورت مناسب نبودن ابعاد انتخابی و تکرار فرآیندهای بالا
توجه: به منظور طراحی و انتخاب ابعاد مناسب برای تیرها معمولاً از جداول ارائه شده در دستورالعملهای مختلف (مشابه جدول زیر) کمک گرفته میشود. در این مثال، ما ابعاد تیر مورد تحلیل را بر اساس جدول زیر انتخاب خواهیم کرد.
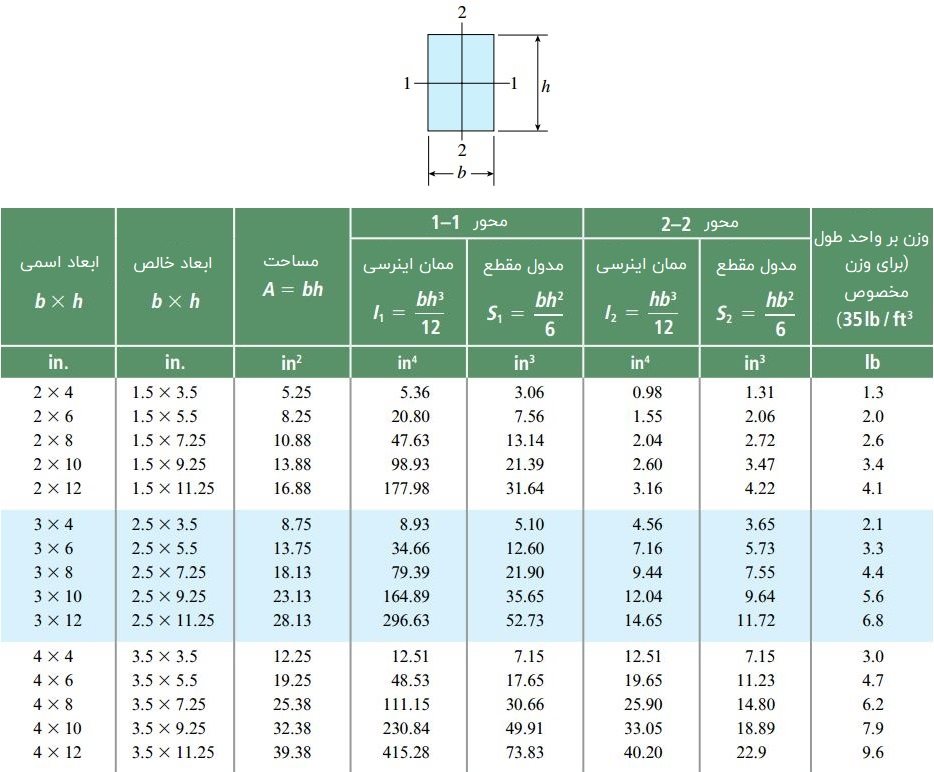
مرحله اول
با توجه به پیکربندی مسئله میتوان دریافت که گشتاور خمشی ماکسیمم در مرکز این تیر رخ میدهد:
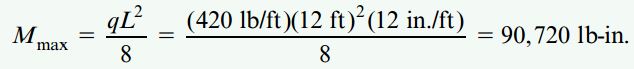
به این ترتیب، مدول مقطع مورد نیاز از رابطه زیر به دست میآید:
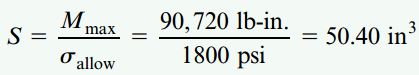
با توجه به مقادیر موجود در جدول، ابعاد سبکترین تیری که قادر به تأمین حداقل مدول مقطع 50.40in3 حول محور 1-1 باشد، برابر با 3*12 اینچ است. مدول مقطع این تیر با 52.73in3 و وزن آن بر واحد طول با 6.8lb/ft برابری میکند.
مرحله دوم
اکنون بار گسترده یکنواخت اعمال شده بر روی تیر به مقدار 426.8lb/ft میرسد (جمع بار q با وزن خود تیر). به این ترتیب، مدول مقطع جدید با مقدار زیر برابر است:
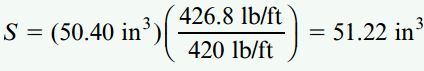
به دلیل کوچکتر بودن مقدار به دست آمده (51.22in3) نسبت به مقدار موجود در جدول (51.73in3)، ابعاد انتخابی (3*12) رضایتبخش خواهد بود.
توجه: اگر وزن مخصوص تیر مورد تحلیل شما با مقدار 35lb/ft3 برابر نبود، میتوانید با تقسیم وزن مخصوص تیر بر 35lb/ft3 و ضرب نسبت به دست آمده در ستون آخر جدول بالا، وزن تیر بر واحد طول را به دست بیاورید.
مثال 2
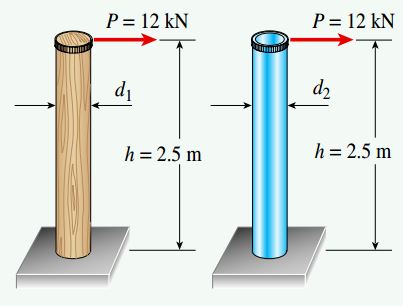
شکل زیر، یک ستون با ارتفاع 2.5 متر را نمایش میدهد که انتهای بالایی آن تحت بار جانبی 12 کیلو نیوتن قرار دارد. برای طراحی این ستون، دو گزینه (ستون چوبی توپر یا لوله آلومینیومی توخالی) پیشنهاد شده است.
- الف: اگر تنش خمشی مجاز چوب برابر با 15 مگا پاسکال باشد، حداقل قطر مورد نیاز d1 ستون چوبی چقدر خواهد بود؟
- ب: اگر تنش خمشی مجاز آلومینیوم برابر با 50 مگا پاسکال و ضخامت دیواره لوله آلومینیومی یک-هشتم قطر خارجی آن باشد، حداقل قطر خارجی مورد نیاز d2 لوله چقدر خواهد بود؟
گشتاور خمشی ماکسیمم
گشتاور ماکسیمم در انتهای پایینی ستون رخ میدهد. این گشتاور از ضرب بار P بر ارتفاع h به دست میآید. بنابراین:
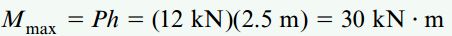
الف: ستون چوبی
مدول مقطع مورد نیاز S1 برای ستون چوبی از رابطه زیر به دست میآید:
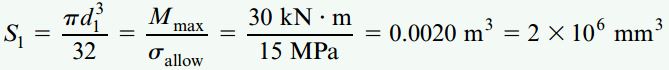
با حل رابطه بالا بر اساس پارامتر d1، قطر این ستون تعیین میشود:
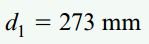
به این ترتیب، قطر انتخابی برای ستون چوبی باید برابر یا بزرگتر از 273 میلیمتر باشد تا میزان تنش ایجاد شده از مقدار مجاز عبور نکند.
ب: لوله آلومینیومی
به منظور تعیین مدول مقطع S2 برای لوله آلومینیومی، ابتدا باید ممان اینرسی I2 مقطع عرضی را تعیین کرد. ضخامت دیواره لوله برابر d2/8 است. بنابراین، قطر داخلی برابر با d2-d2/4 یا 0.75d2 خواهد بود. به این ترتیب، برای ممان اینرسی I2 داریم:
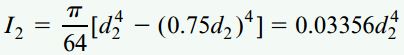
اکنون میتوانیم رابطه بین مدول مقطع لوله و قطر خارجی آن را به دست بیاوریم:
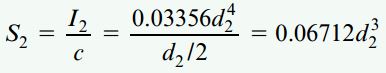
مدول مقطع مورد نیاز از رابطه زیر تعیین میشود:
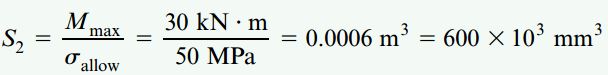
اگر دو رابطه قبلی را با هم برابر قرار دهیم، قطر خارجی لوله آلومینیومی قابل محاسبه خواهد بود:

به این ترتیب، قطر داخلی لوله برابر با 0.75*(208mm) یا 156mm است.
مثال 3
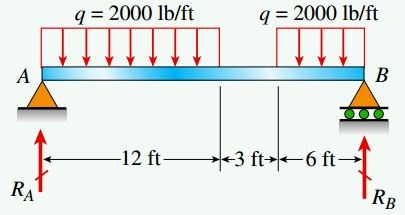
شکل زیر، یک تیر ساده با طول 21 فوت را نمایش میدهد که در معرض یک بار گسترده یکنواخت q=2000lb/ft قرار دارد. نحوه توزیع بار و محدودههای اعمال آن در شکل قابل مشاهده است.
با فرض تنش خمشی مجاز 18000psi و در نظر گرفتن وزن تیر به همراه بار یکنواخت، ابعاد مناسب یک تیر بال پهن برای تحمل بارهای وارده چقدر خواهد بود؟
برای حل این مسئله، مراحل زیر را دنبال میکنیم:
- تعیین گشتاور خمشی ماکسیمم ناشی از اعمال بار یکنواخت
- محاسبه مدول مقطع با استفاده از گشتاور ماکسیمم به دست آمده
- انتخاب آزمایشی ابعاد تیر بال پهن با توجه به جدول زیر
- محاسبه مقدار جدید گشتاور خمشی و مدول مقطع با استفاده از وزن مخصوص نوشته شده در جدول
- ارزیابی رضایتبخش بودن تیر انتخاب شده
- انتخاب یک تیر بزرگتر در صورت مناسب نبودن ابعاد انتخابی و تکرار فرآیندهای بالا
گشتاور خمشی ماکسیمم
برای یافتن محل رخ دادن گشتاور خمشی ماکسیمم، میتوانیم از رسم نیروی برشی کمک بگیریم. روشهای رسم این نمودار در مقالات «نمودار نیروی برشی و گشتاور خمشی» و «مثالهای طبقهبندیشده رسم نمودار نیروی برشی و گشتاور خمشی» به طور کامل مورد بحث قرار گرفتهاند.
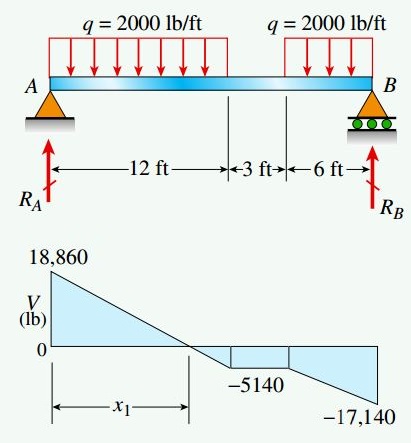
به منظور تعیین گشتاور خمشی ماکسیمم، ابتدا باید عکسالعملهای تکیهگاهی را به دست بیاوریم:
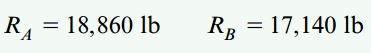
فاصله x1 از تکیهگاه چپ تا سطح مقطعی با نیروی برشی صفر با استفاده از رابطه زیر محاسبه میشود:
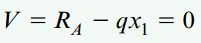
این رابطه برای محدوده x بین 0 تا 12 فوت معتبر است. با حل رابطه بالا بر حسب x1 خواهیم داشت:
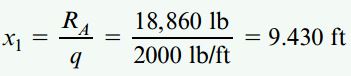
به دلیل کمتر بودن فاصله به دست آمده (9.430ft) از حداکثر فاصله مجاز (12ft)، صحت محاسبات صورت گرفته تأیید میشود. گشتاور خمشی ماکسیمم بر روی مقطعی با نیروی برشی صفر رخ میدهد. بنابراین:
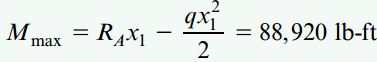
مدول مقطع مورد نیاز
مدول مقطع مورد نیاز با توجه به بار q و از طریق رابطه زیر به دست میآید:
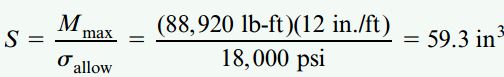
ابعاد آزمایشی تیر
بر اساس نتایج به دست آمده در مراحل قبل و جدول ارائه شده در ابتدای مسئله، سبکترین تیر بال پهن با مدول مقطع بزرگتر از 59.3in3 را انتخاب میکنیم. مدل این تیر دارای، W12*50 با مدول مقطع S=64.7in3 است. وزن این تیر بر واحد طول با مقدار 50lb/ft برابری میکند.
اکنون باید با در نظر گرفتن وزن تیر به همراه بار q، عکس عملهای تکیهگاهی، گشتاور خمشی ماکسیمم و مدول مقطع مورد نیاز را مجدداً محاسبه کنیم. عکسالعملهای تکیهگاهی ناشی از اعمال ترکیب این دو بار به صورت زیر خواهند بود:

فاصله x1 نیز به صورت زیر محاسبه میشود:
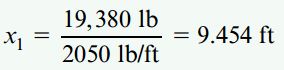
گشتاور خمشی ماکسیمم به مقدار 91610lb-ft افزایش مییابد. به این ترتیب، مدول مقطع جدید با استفاده از رابطه زیر به دست میآید:
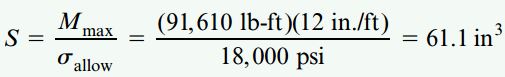
با توجه به کمتر بودن مقدار مدول مقطع جدید (61.1in3) نسبت به مدول مقطع تیر انتخابی (64.7in3)، تیر W12*15 برای طراحی مناسب خواهد بود.
توجه: اگر مدول مقطع جدید از مدول مقطع تیر W12*15 بیشتر میبود، باید یک تیر با مدول مقطع بزرگتر را انتخاب و مراحل قبلی را دوباره تکرار میکردیم.
مثال 4
شکل زیر، یک سد موقت چوبی را نمایش میدهد که از کنار هم قرار دادن چند تخته افقی تشکیل شده است. این سد توسط ستونهای چوبی عمودی نگهداری میشود. ستونهای مذکور درون زمین قرار گرفته و همانند یک تیر یکسر گیردار عمل میکند. سطح مقطع ستونهای چوبی به شکل مربع (با ابعاد b*b) و فاصله بین مرکز آنها s=0.8m است. اگر ارتفاع آب پشت سد برابر با h=12m و تنش خمشی مجاز چوب برابر با σallow=8.0MPa باشد، حداقل ابعاد مورد نیاز برای هر ستون چقدر خواهد بود؟
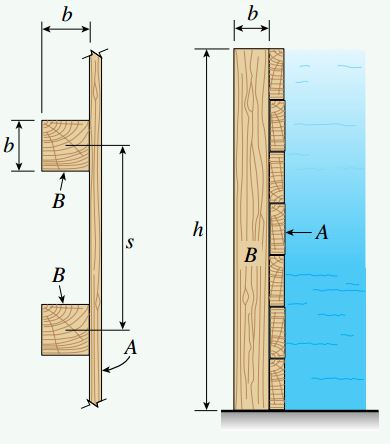
نمودار بارگذاری
با اعمال فشار آب بر روی تختهها، هر ستون در معرض یک بار گسترده مثلثی قرار میگیرد. نمودار بارگذاری برای هر ستون مانند شکل زیر خواهد بود.
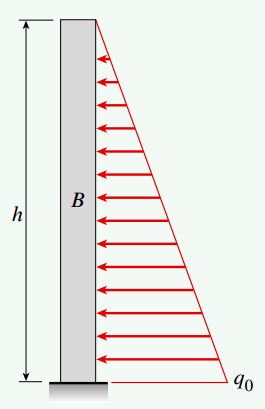
حداکثر مقدار شدت بار (q0) اعمال شده بر روی هر ستون از حاصلضرب فاصله بین ستونها در فشار آب در عمق h به دست میآید:
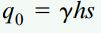
q0: حداکثر مقدار شدت بار بر حسب نیرو بر واحد فاصله؛ γ: وزن مخصوص آب بر حسب نیرو بر واحد حجم؛ h؛ ارتفاع ستون بر حسب واحد فاصله؛ s: فاصله بین ستونها بر حسب واحد فاصله
مدول مقطع
در این مسئله، هر ستون را میتوان به عنوان یک تیر یکسر گیردار در نظر گرفت. از اینرو، گشتاور خمشی ماکسیمم درون هر ستون در پایینترین قسمت آن رخ میدهد. این گشتاور ماکسیمم با استفاده از رابطه زیر محاسبه میشود:
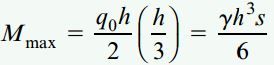
به این ترتیب، مدول مقطع مورد نیاز به صورت زیر خواهد بود:
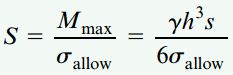
مدول مقطع یک تیر با سطح مقطع مربعی برابر با S=b3/6 است. با جایگذاری S در رابطه بالا، امکان تعیین حداقل ابعاد ستون فراهم میشود:
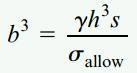
مقادیر عددی
اکنون مقادیر عددی را در رابطه حداقل ابعاد ستون وارد میکنیم:
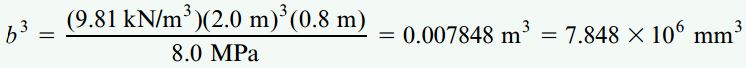
به این ترتیب:
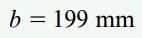
در نتیجه، حداقل بعد مورد نیاز ستونها باید برابر با 199 میلیمتر باشد. با انتخاب ابعاد بزرگتر (مثلاً 200 میلیمتر)، از کمتر بودن مقدار تنش خمشی واقعی نسبت به تنش مجاز اطمینان حاصل میشود.
توجه: در هنگام حل مثالهای واقعی، باید ابعاد تیرهای چوبی یا فولادی مورد نیاز را از جداول موجود در استانداردهای مورد استفاده انتخاب کنید. اگر با چندین گزینه احتمالی رو به رو شدید، انتخاب سبکترین تیر متناسب با مدول مقطع مورد نیاز را به شما پیشنهاد میکنیم.
^^













سلام
محاسبه حداکثر تحمل بار متمرکز بروی تیرآهن ۱۴ IPE بطول ۵ متر چگونه است؟
خیلی ممنون