معادله کوشی ریمان — به زبان ساده (+ دانلود فیلم آموزش رایگان)

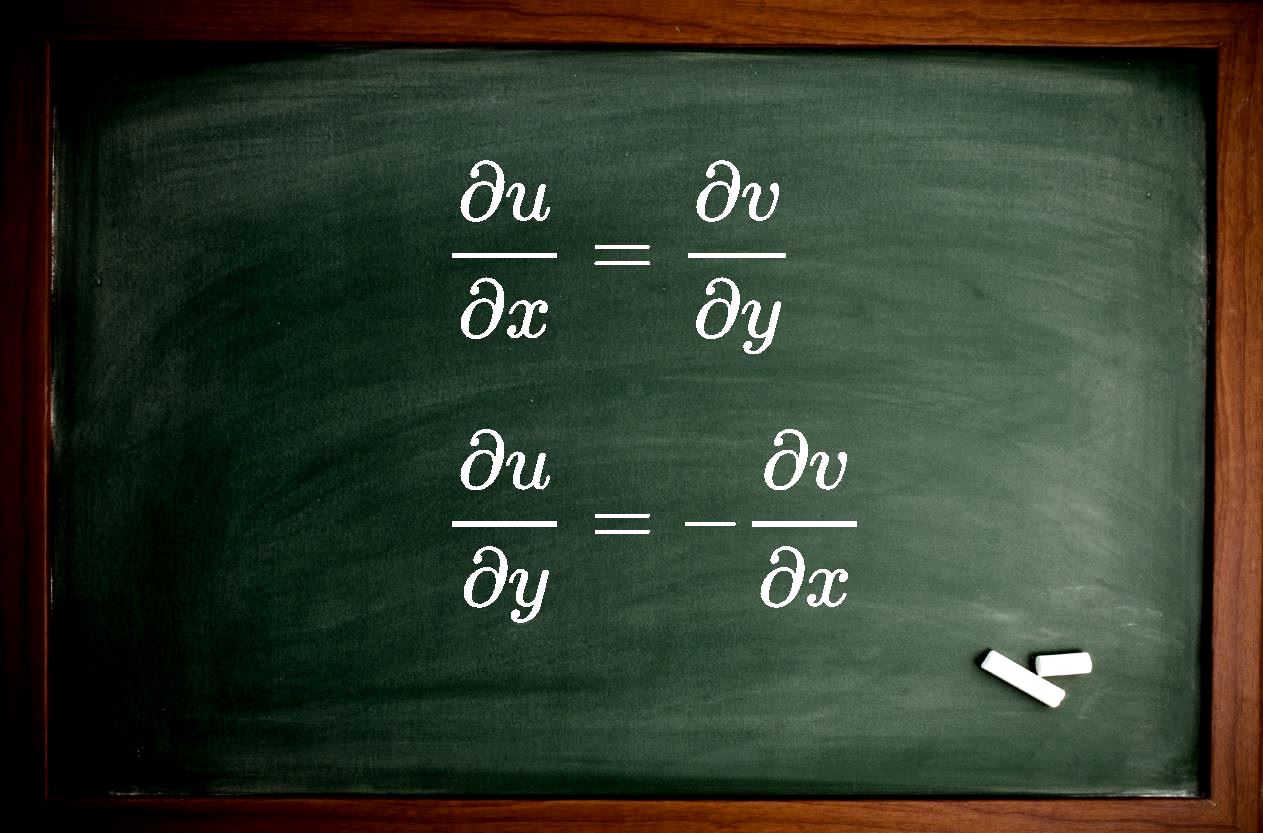
در مطالب پیش‌تر وبلاگ فرادرس، در مورد حد و مشتق در توابع مختلط بحث شد. هما‌ن‌طور که بیان شد، یک تابع مختلط را می‌توان به صورت حاصل جمع یک بخش حقیقی و یک بخش موهومی بیان کرد. از طرفی اگر چنین تابعی مشتق‌پذیر باشد در این صورت می‌توان روابطی خاص را بین بخش حقیقی و موهومی آن بیان کرد. در این مطلب قصد داریم تا معادله‌ای تحت عنوان معادله کوشی ریمان را معرفی کرده و مثال‌هایی نیز از آن ارائه دهیم.

معادله کوشی ریمان

به منظور معرفی معادله کوشی ریمان در ابتدا از تعریف مشتق آغاز می‌کنیم. بدین منظور تابعِ مختلط $$ f ( z ) $$ را به صورت زیر در نظر بگیرید.

$$ f ( z ) = u + i v $$

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

حال فرض کنید تابع فوق مشتق‌پذیر باشد. در این صورت با توجه به تعریف، این مشتق را می‌توان در قالب حد، به شکل زیر بیان کرد:

$$ f ^ { \prime } ( z ) = \lim _ { t \rightarrow 0 } \frac { f ( z + t ) - f ( z ) } { t } = \lim _ { t \rightarrow 0 } \frac { f ( z + i t ) - f ( z ) } {‌ i t } $$

در رابطه فوق $$ t $$ مقداری حقیقی است. در نتیجه اثبات فوق را می‌توان در قالب $$ u , v$$ به شکل زیر بازنویسی کرد.

$$ \begin {aligned} \lim _ { t \rightarrow 0 } \frac { f ( z + t ) - f ( z ) } { t } & = \lim _ { t \rightarrow 0 } \frac { u ( x + t , y ) + i v ( x + t , y ) - u ( x , y ) - i v ( x , y ) } { t } \\ & = \lim _{t \rightarrow 0} \frac{u(x+t, y)-u(x, y ) } { t } + i \lim _ { t \rightarrow 0 } \frac { v ( x + t , y ) - v ( x , y ) } { t } = \frac { \partial u } { \partial x } + i \frac { \partial v } { \partial x } \end {aligned} $$

حال فرض کنید حد فوق در راستای مقدار موهومی $$ i t $$ محاسبه شود. در این حالت می‌توان آن را به صورت زیر بیان می‌شود.

$$ \begin{aligned} \lim _ { t \rightarrow 0 } \frac { f ( z + i t ) - f ( z ) } { i t } & = - i \lim _ { t \rightarrow 0 } \frac { u ( x , y + t ) + i v ( x , y + t ) - u ( x , y ) - v ( x , y ) } { t } \\ & = - i \lim _ { t \rightarrow 0 } \frac { u ( x , y + t ) - u ( x , y ) } { t } + \lim _ { t \rightarrow 0 } \frac { v ( x , y + t ) - v ( x , y ) } { t } = - i \frac { \partial u } { \partial y } + \frac { \partial v } { \partial y } \end {aligned} $$

با توجه به مشتق‌پذیر بودن $$ f $$، می‌توان گفت که بخش‌های حقیقی و موهومی در دو عبارت فوق با هم برابر هستند. در نتیجه با اعمال این برابری داریم:

$$ \begin {align*} \frac { \partial u } { \partial x } & = \frac { \partial v } { \partial y } \\ \frac { \partial v }{\partial x } & = - \frac { \partial u } { \partial y } \end {align*} $$

نهایتا مشتق تابع را نیز می‌توان به صورت زیر بیان کرد:

$$ \boxed { f ^ { \prime } ( z ) = \frac { \partial u } { \partial x } + i \frac { \partial v } { \partial x } = \frac { \partial v } { \partial y } - i \frac { \partial u } { \partial y } } $$

برای نمونه تابع مختلط $$ z ^ { 2 } = \left( x ^ { 2 } - y ^ { 2 } \right) + 2 x y i $$ را در نظر بگیرید. مشتقات جزئی بخش‌های حقیقی و موهومی نسبت به متغیر‌های $$ x $$ و $$ y $$ برابرند با:

$$ \frac { \partial } { \partial x } \left ( x ^ { 2 } - y ^ { 2 } \right) = 2 x = \frac { \partial } { \partial y } ( 2 x y ) \quad \text { , } \quad \frac { \partial } { \partial x } ( 2 x y ) = 2 y = - \frac { \partial } { \partial y } \left( x ^ { 2 } - y ^ { 2 } \right) $$

برای تابع $$ e ^ { z } = e ^ { x } \cos y + i e ^ { x } \sin y $$ نیز می‌توان همین گزاره را بیان کرد، چرا که می‌توان گفت:

$$\begin {align*} \frac { \partial } { \partial x } \left( e ^ { x } \cos y \right) & = e ^ { x } \cos y \\ & = \frac { \partial } { \partial y } \left( e ^ { x } \sin y \right) \ \text { , } \ \frac { \partial } { \partial x } \left( e ^ { x } \sin y \right ) = e ^ { x } \sin y \\ & = - \frac { \partial } { \partial y } \left( e ^ { x } \cos y \right) \end {align*} $$

بنابراین معادله کوشی-ریمان برای این تابع صادق بوده و تابع مشتق‌پذیر است. مشتق تابع نیز برابر است با:

$$ \frac { d } { d z } e ^ { z } = \frac { \partial } { \partial x } \left( e ^ { x } \cos y \right) + \frac { \partial } { \partial x } \left( e ^ { x } \sin y \right ) = e ^ { x } \cos y + e ^ { x } \sin y = e ^ { z } $$

توجه داشته باشید که معادله کوشی ریمان برای هر تابع تحلیلی صدق می‌کند.

مثال ‍۱

تابع مختلط $$ f ( z ) = y - 2 x y + i \left( - x + x ^ { 2 } - y ^ { 2 } \right) + z ^ { 2 } $$ را در نظر بگیرید. به ازای چه مقادیری از $$ z $$، تابع $$ f $$ مشتق‌پذیر است.

در اولین قدم باید تابع را بر حسب $$ x , y $$ بیان کرد. با قرار دادن $$ z = x + i y $$ در معادله، بخش‌های حقیقی و موهومی به صورت زیر بدست می‌آیند.

$$ \begin {aligned} f ( z ) & = y - 2 x y + i \left( - x + x ^ { 2 } - y ^ { 2 } \right) + x ^ { 2 } - y ^ { 2 } + 2 i x y \\ & = x ^ { 2 } - 2 x y + y - y ^ { 2 } + i \left( - x + 2 x y + x ^ { 2 } - y ^ { 2 } \right) \end {aligned} $$

در مرحله بعد مشتقات جزئی بخش‌های حقیقی و موهومی نسبت به $$ x , y $$ برابر می‌شوند با:

$$ \begin {array} {ll} {u _ { x } ( x , y ) = 2 x - 2 y } & { v _ { x } ( x , y ) = - 1 + 2 y + 2 x } \\ { u _ { y } ( x , y ) = - 2 x + 1 - 2 y } & { v _ {‌ y } ( x , y ) = 2 x - 2 y } \end {array} $$

با توجه به مشتق‌پذیر بودن $$ f $$، دو رابطه زیر باید برقرار باشند.

$$ u _ { x } = v _ { y } \ \quad , \quad v _ { x } = - u _ { y } $$

اما مشتقات بدست آمده نشان می‌دهند که به ازای تمامی مقادیر $$ x , y $$، دو تساوی فوق برقرار هستند. اما جهت درک بهتر می‌توان $$ f $$ را بر حسب $$ z $$ نیز بیان کرد. در ادامه این کار انجام شده است.

$$ f ^ { \prime } ( z ) = u _ { x } + i‌ v _ { x } = 2 x - 2 y + i ( 2 x + 2 y - 1 ) = 2 z + 2 i z - i $$

البته این تابع را می‌توان در قالب رابطه زیر نیز بیان کرد:

$$ f ( z ) = z ^ { 2 } + i z ^ { 2 } - i z $$

نهایتا می‌توان گفت که تابع $$ f $$، تابعی چند‌جمله‌ای بر حسب $$ z $$ است.

مثال ۲

نشان دهید که تابع $$ f ( z ) = ( \overline { z } + 1 ) ^ { 3 } - 3 \overline { z } $$ در هیچ نقطه‌ای تحلیلی نیست.

همان‌طور که بیان شد در اولین گام باید تابع را بر حسب $$ x , y $$ بیان کرد:

$$ \begin {aligned} f ( z ) & = ( x + 1 - y i ) ^ { 3 } - 3 ( x - y i ) \\ & = ( x + 1 ) ^ { 3 } - 3 ( x + 1 ) y ^ { 2 } - 3 ( x + 1 ) ^ { 2 } y i + y ^ { 3 } i - 3 x + 3 y i \\ &‌ = \underbrace { ( x + 1 ) ^ { 3 } - 3 ( x + 1 ) y ^ { 2 } - 3 x } _ { u ( x , y ) ‌} + \underbrace { i \left( y ^ { 3 } + 3 y - 3 ( x + 1 ) ^ { 2 } y \right) } _ { v ( x , y ) } \end {aligned} $$

در مرحله بعد مشتقات نسبت $$ x $$ و $$ y $$ توابع $$ u , v $$ برابرند با:

$$ \begin{array}{ll} { u _ { x } = 3 ( x + 1 ) ^ { 2 } - 3 y ^ { 2 } - 3 } & { v _ { x } = - 6 ( x +1 ) y } \\ { u _ { y } = - 6 ( x + 1 ) y } & { v _ { y } = 3 y ^ { 2 } + 3 - 3 ( x + 1 ) ^ { 2 } } \end {array} $$

همان‌طور که محاسبه شد، عبارت‌های بدست آمده دقیقا عکس شرایط کوشی ریمان است. بنابراین تابع ارائه شده در هیچ نقطه‌ای شرایط کوشی ریمان را ارضا نمی‌کند. در حقیقت در عبارات بدست آمده در بالا $$ v _ { x } = u _ { y } $$ و $$ u _ { x } = - v _ { y } $$ است.

مثال ۳

نشان دهید که اگر تابع $$ f $$ تحلیلی است در این صورت دو رابطه زیر برقرار هستند.

$$ \displaystyle { \mid f ^ { \prime } ( z ) \mid ^ 2 = \left ( \frac { \partial u } { \partial x } \right ) ^ 2 + \left ( \frac { \partial v } { \partial x } \right ) ^ 2 } $$

$$\displaystyle { \mid f ^ { \prime } ( z ) \mid ^ 2 = \left ( \frac { \partial u } { \partial y } \right ) ^ 2 + \left ( \frac { \partial v } { \partial y } \right ) ^ 2 } $$

با توجه به تحلیل بودن تابع $$ f $$، مشتق آن را می‌توان مطابق با رابطه زیر بیان کرد:

$$ \begin {align} \quad f ^ { \prime } ( z ) = \frac { \partial u } { \partial x } + i \frac { \partial v } { \partial x } \end {align} $$

بنابراین اندازه مشتق تابع نیز برابر است با:

$$ \begin {align} \quad \mid f ^ { \prime } ( z ) \mid = \sqrt { \left( \frac { \partial u } { \partial x } \right ) ^ 2 + \left ( \frac { \partial v}{\partial x} \right )^2} \end {align} $$

بدیهی است که رابطه فوق را نیز می‌توان به صورت زیر بازنویسی کرد.

$$ \begin {align} \quad \mid f ^ { \prime } ( z ) \mid ^ 2 = \left( \frac { \partial u } { \partial x } \right ) ^ 2 + \left ( \frac{\partial v } { \partial x } \right ) ^ 2 \end {align}$$

در صورتی که مطلب فوق برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مانده تابع — به زبان ساده
• تابع مختلط — به زبان ساده
• تابع هارمونیک — به زبان ساده

^^