قانون دالتون چیست؟ – به زبان ساده + مثال

قانون دالتون یکی از مهم‌‌ترین مواردی است که در مطالعه قانون گاز‌ها در علم شیمی وجود دارد. از این قانون می‌توان برای به دست آوردن فشار یک سیستم از طریق فشارهای جزئی هر کدام از گازها بهره برد بنابراین تسلط بر روابط قانون دالتون برای دانشجویان رشته شیمی و افراد فعال در این حوزه اهمیت به‌سزایی دارد و به آن‌ها کمک می‌کند تا بتوانند با سیستم‌های گازی کار کنند و اطلاعات لازم را از آن‌ها استخراج کنند.

در این مطلب مجله فرادرس ابتدا قانون دالتون را معرفی می‌کنیم و روابط مسلط بر آن را مرور خواهیم کرد. سپس با نگاهی به مخلوط گازها، فشار جزئی آن‌ها را در سیستم‌ها بررسی می‌کنیم. یکی از مهم‌ترین مولفه‌های موجود در روابط قوانین دالتون، کسر مولی است که به معرفی آن نیز خواهیم پرداخت. سپس قانون دالتون را در گازهای حقیقی مورد بررسی قرار می‌دهیم. در نهایت نیز تعدادی مثال و تمرین را حل خواهیم کرد زیرا آشنایی با این مفهوم مستلزم این است که توانایی حل مسائل مرتبط، به کمک روابط آن را داشته باشیم.

قانون دالتون چیست؟

«قانون دالتون» (Dalton's Law) که با نام «قانون فشارهای جزئی» (Law of Partial Pressures) نیز شناخته می‌شود، بیان‌کننده این است که فشار کلی حاصل از مخلوطی از گازها برابر با مجموع فشارهای جزئی هر کدام از آن‌ها است. با توجه به نظریه سینتیک شیمیایی گازها، اگر گازی در محفظه‌ای قرار داشته باشد، پخش می‌شود تا کل فضای آن را اشغال کند. به عبارتی می‌توان گفت که مولکول‌ها در مخلوطی از گازها چنان فاصله زیادی از یکدیگر دارند که آزادانه و مستقل رفتار می‌کنند و با یکدیگر برهم‌کنشی نخواهند داشت.

رابطه قانون دالتون

فشار یک گاز ایده‌ال از برخوردهای مولکول‌های آن با جداره محفظه محاسبه می‌شود و در آن برخورد با مولکول‌های دیگر گازی موثر نیست زیرا بسیار ناچیز است. گازی که در محفظه‌ای در مخلوطی از گازها وجود دارد، پخش می‌شود تا کل محفظه را در بر بگیرد و در این کار تاثیری روی فشار گازهای دیگر نخواهد داشت. بنابراین می‌توان این‌طور جمع‌بندی کرد که فشار گازی مشخص تنها به تعداد مول‌های آن و حجم و دمای سیستم بستگی دارد.

از آن‌جا که گازها در مخلوط گازی، در یک محفظه واحد قرار دارند، حجم و دمای آن‌ها مشابه یکدیگر خواهد بود. در این صورت هر گاز، فشار مخصوص به خود را دارد و می‌توان از مجموع آن‌ها به فشار کل مخلوط گازی رسید. این گفته را می‌توان توسط رابطه زیر نشان داد.

$$P_{total} = P_A + P_B + ...$$

در ادامه می‌خواهیم بدانیم هر یک از مولفه‌های این رابطه به چه چیزی اشاره دارند.

• $$P_{total}$$: فشار کل گازها
• $$P_A$$: فشار جزئی گاز $$A$$
• $$P_B$$: فشار جزئی گاز $$B$$

در صورتی که در مخلوط گازها، اجزای بیشتری مانند گاز $$C$$ و گاز $$D$$ نیز حضور داشته باشد، فشار جزئی آن‌ها را به‌‌صورت $$P_C$$ و $$P_D$$ در رابطه بالا وارد می‌کنیم.

فشار جزئی چیست؟

همان‌طور که مشاهده کردید، یکی از مولفه‌های مهم در قانون دالتون فشار جزئی نامیده می‌شود. در این بخش می‌خواهیم بدانیم مفهوم آن برای گاز چیست. با توجه به قانون گازهای ایده‌آل، تمامی گازها رفتاری مشابه یکدیگر دارند که فارغ از نیروهای جاذبه و دافعه بین آن‌هاست.

در صورتی که مقدار حجم و دمای آن‌ها ثابت نگه داشته شود، می‌توان نشان داد که فشار یک سیستم با تعداد مول‌های آن رابطه مستقیم دارد.

$$P=n \left(\dfrac{RT}{V}\right) = n \times \rm const$$

همان‌طور که مشاهده می‌کنید هیچ‌یک از مولفه‌های این رابطه به ماهیت و نوع گاز بستگی ندارد و تنها تعداد مول‌های آن است که اهمیت دارد. حال موقعیتی را تصور کنید که در آن دو گاز ایده‌‌آل به مقدار برابر با یکدیگر در یک مخلوط حضور دارند. در این صورت می‌خواهیم بدانیم فشار کل سیستم را به چه طریقی می‌توان به دست آورد. از آن‌جا که مقدار دو گاز با یکدیگر برابر است و تنها به مقدار هر جزء بستگی دارد، فشار کل سیستم دو برابر فشار هر کدام از آن‌ها است.

به‌طور کلی می‌توان اینطور بیان کرد که فشار حاصل از مخلوطی از گازها در دمایی خاص برابر با مجموع فشارهای هر کدام از آن‌ها در حالتی است که جداگانه حضور دارند. این فشار مجزا را با نام فشار جزئی می‌شناسیم و می‌توان مقدار آن را با در دست داشتن حجم، دما و تعداد مول‌ها به دست آورد. این همان قانون دالتون است که اولین بار توسط «جان دالتون» (John Dalton) بیان شد. در حالت کلی و در حضور چند گاز می‌توان رابطه قانون دالتون را به‌صورت زیر نشان داد.

$$ \begin{align} P_{tot} &= P_1+P_2+P_3+P_4 \ldots \\[4pt] &= \sum_{i=1}^n{P_i} \label{10.6.2} \end{align}$$

برای مثال سیستمی را در نظر بگیرید که در آن سه گاز هلیوم با فشار جزئی ۱ اتمسفر، گاز نیتروژن با فشار جزئی ۱ اتمسفر و گاز اکسیژن با فشار جزئی ۱ اتمسفر وجود دارد. در این صورت فشار سیستم را می‌توان از مجموع فشارهای جزئی این سه گاز به دست آورد که برابر با ۳ اتمسفر خواهد بود. این را می‌توانید به‌صورت ساده در تصویر زیر مشاهده کنید.

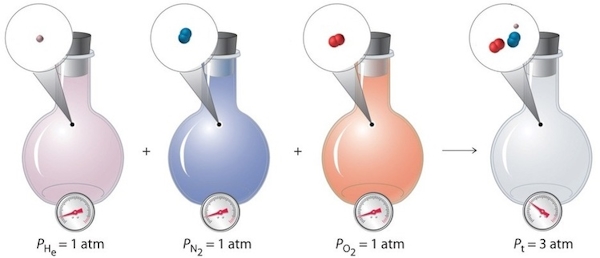
مخلوط گازها در قانون دالتون

با توجه به قوانین مسلط بر گازهای‌ایده‌آل، می‌توانیم رابطه زیر را بین مولفه‌های مختلف آن برقرار کنیم.

$$PV = nRT$$

در صورتی که ترکیبات مولی گازها را بدانیم، می‌توانیم معادله زیر را نیز داشته باشیم.

$$n_{total} = n_a + n_b + ...$$

در اینجا نیز با توجه به قانون گازها و قانون گاز ایده‌آل، می‌توان قانون دالتون را برای تعداد مول‌های مخلوط گازی به کار برد، بنابراین مجموع تعداد مول‌های هر کدام از گازها در یک مخلوط، برابر با کل تعداد مول‌های گازی مخلوط است. در این صورت فشار، دما و حجم در سیستم ثابت نگه داشته می‌شوند. حجم کل گازها را نیز می‌توان به همین روش به دست آورد، گرچه این روش متدوال نیست. در نهایت به رابطه زیر برای مخلوطی گازی می‌رسیم.

$$P_{total} V=n_{total} RT$$

با بازآرایی این رابطه می‌توان از آن برای به دست آوردن تعداد مول‌های گازی کل استفاده کرد. در برخی مثال‌ها، جرم هر کدام از نمونه‌های گازی داده شده است و هدف به دست آوردن فشار کل است. در این صورت می‌توان با تبدیل گرم به مول و استفاده از قانون دالتون به پاسخ مورد نظر رسید.

برای مثال در صورتی که در سیستمی دو گاز $$A$$ و $$B$$ وجود داشته باشد، می‌توان از رابطه زیر فشار آن را به دست آورد.

$$ \begin{align} P_{tot} &=P_A+P_B \\[4pt] &=n_A\left(\dfrac{RT}{V}\right) + n_B\left(\dfrac{RT}{V}\right) \\[4pt] &=(n_A+n_B)\left(\dfrac{RT}{V}\right) \label{10.6.3} \end{align}$$

رابطه کلی دیگری نیز برای به دست آوردن فشار کل سیستمی با چند جزء گازی وجود دارد که آن را در زیر آورده‌ایم.

$$ \begin{align} P_{tot} &=(P_1+P_2+P_3+ \; \cdots +P_n)\left(\dfrac{RT}{V}\right)\label{10.6.2a} \\[4pt] &=\sum_{i=1}^n{P_i}\left(\dfrac{RT}{V}\right)\label{10.6.2b} \end{align}$$

این رابطه را می‌توان برای تمامی گازهای ایده‌‌‌آل به کار برد. در ادامه به بررسی مثالی می‌پردازیم که در آن از این روابط استفاده شده است.

مثال از قانون دالتون در غواصی

کپسول‌هایی که غواص‌ها در اعماق زیاد از آن برای تنفس استفاده می‌کنند از مخلوط خاصی از گازها تشکیل شده است. غواص‌ها در عمق ۳۵۰ فوت با فشار ۱۰ اتمسفر روبرو می‌شوند. کپسول گاز آن‌ها در این حالت حاوی ۵۱٫۲ گرم اکسیژن و ۳۲۶٫۴ گرم هلیوم است و ۱۰ لیتر حجم دارد. در صورتی که دما برابر با ۱۰ درجه سانتی‌گراد باشد، فشار جزئی هر یک از گازها را به دست آورید. همچنین فشار کل سیستم را محاسبه کنید.

پاسخ

برای رسیدن به فشارهای جزئی ابتدا باید تعداد مول‌های هر یک از گازها را داشته باشیم که می‌توان آن را از جرم آن‌ها به‌صورت زیر به دست آورید. در هر مورد جرم گاز را تقسیم بر جرم مولکولی آن می‌کنیم.

$$n_{\rm He}=\rm\dfrac{326.4\;g}{4.003\;g/mol}=81.54\;mol \nonumber$$

تعداد مول‌های اکسیژن را نیز به‌صورت زیر به دست می‌آوریم.

$$n_{\rm O_2}=\rm \dfrac{51.2\;g}{32.00\;g/mol}=1.60\;mol \nonumber$$

سپس از رابطه گازهای ایده‌‌آل برای به دست آوردن فشار هر گاز استفاده می‌کنیم.

$$P_{\rm He}=\dfrac{n_{\rm He}​RT}{V}=\rm\dfrac{81.54\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=196.2\;atm \nonumber$$

$$P_{\rm O_2}=\dfrac{n_{\rm O_2}​ RT}{V}=\rm\dfrac{1.60\;mol\times0.08206\;\dfrac{atm\cdot L}{mol\cdot K}\times293.15\;K}{10.0\;L}=3.85\;atm \nonumber$$

از آنجا که فشار کل هر سیستم از مجموع فشارهای جزئی به دست می‌آید، رابطه زیر صدق می‌کند.

$$P_{\rm tot}=P_{\rm He}+P_{\rm O_2}=\rm(196.2+3.85)\;atm=200.1\;atm \nonumber$$

قانون دالتون در مخلوط گاز با بخار آب

از قانون دالتون و روابط مسلط بر فشارهای جزئی می‌توان در سیستمی بسته متشکل از یک گاز و آب استفاده کرد. فشار کل این سیستم برابر با فشار حاصل از این گاز روی مایع است. توجه داشته باشید که همیشه مقداری از بخارات آب روی این گاز وجود خواهد داشت که از فرآيند تبخیر آب به دست می‌آید. برای انجام محاسبات در این مورد می‌توان از فشار کل سیستم و فشارهای جزئی استفاده کرد.

کسر مولی

از فشار جزئی یک گاز و فشار کلی مخلوط آن، می‌توان کسر مولی آن گاز را به دست آورد. «کسر مولی» (Mole Ration) را با نماد $$Xi$$ نشان می‌دهند و نسبت هر جزء را در مخلوط گازی به دست می‌دهد. کسر مولی کمیتی فاقد واحد است.

برای درک بهتر در این مورد مثالی را بررسی می‌کنیم. در صورتی که فشار اکسیژن در مخلوطی برابر با ۴ اتمسفر و فشار کل آن سیستم برابر با ۱۰ اتمسفر باشد، کسر مولی اکسیژن در این مخلوط برابر با ۰٫۴ است. برای به دست آوردن این مولفه می‌توان از فشار، حجم و تعداد مول‌‌ها استفاده کرد و رابطه مربوط به آن‌ها را در زیر آورده‌ایم.

$$X_i=\dfrac{P_i}{P_{tot}}=\dfrac{n_i}{n_{tot}}=\dfrac{V_i}{V_{tot}} \tag{5}$$

از کسر مولی برای به دست آوردن ترکیبات موجود در یک گاز استفاده می‌شود. در یک مخلوط مجموع کسر مولی‌های اجزای مختلف باید برابر با عدد ۱ باشد زیرا کسر مولی نشان‌دهنده نسبت گازها در یک مخلوط است. در ادامه می‌خواهیم به بررسی مثالی بپردازیم که در آن از کسر مولی برای رسیدن به پاسخ کمک گرفته شده است.

مثال از کسر مولی

مخلوطی از ۷ گرم گاز نیتروژن و ۸ گرم گاز آرگون در سیلندری وجود دارد. در صورتی که فشار کل سیستم برابر با ۲۷ بار باشد، فشار جزئی گاز نیتروژن را محاسبه کنید. (جرم اتمی نیتروژن برابر با ۱۴ گرم بر مول و جرم اتمی آرگون برابر با ۴۰ گرم بر مول است.)

پاسخ

از آن‌جا که جرم هر گاز را داریم، می‌توانیم تعداد مول‌های آن‌ها را نیز محاسبه کنیم. این کار را با تقسیم جرم بر جرم اتمی آن‌ها به‌صورت زیر انجام می‌دهیم. توجه داشته باشید که نیتروژن به شکل مولکولی $$N_2$$ وجود دارد و باید جرم اتمی آن را ۲ برابر کرد.

$${n_{N_2}}=\frac{7\;g}{28\;g/mol}=0.25\;mol$$

$${n_{Ar}}=\frac{8\;g}{40\;g/mol}=0.20\;mol$$

سپس با در دست داشتن تعداد مول‌های هر گاز، کسر مولی نیتروژن را به دست می‌آوریم.

$${X_{N_2}}=\frac{0.25}{0.25+0.20}=\frac{5}{9}$$

از ضرب کسر مولی نیتروژن در فشار کل سیستم می‌توان فشار جزئی نیتروژن را به دست آورد.

$$P_{N_2 }=X_{N_2}\times P_{total}=\frac{5}{9}\times27=15\;bar$$

قانون دالتون برای گازهای حقیقی

«گازهای حقیقی» (Real Gases) گازهایی هستند که رفتار ایده‌‌آلی از خود نشان نمی‌دهند به این معنی که یک یا چند قانون نظریه سینتیک گازها را نقض می‌کنند. با این حال در صورتی که گازهای حقیقی در فشار پایین یا دمای بالا باشند، مانند گازهای ایده‌آل رفتار می‌کنند.

از این رو در فشار بالا و دمای پایین نمی‌توان برای آن‌ها از قانون دالتون استفاده کرد، زیرا واکنش‌پذیری گازها بالاتر است و احتمال تغییر فشار سیستم وجود دارد. برای مثال در صورتی که بین مولکول‌ها جاذبه وجود داشته باشد، به یکدیگر نزدیک خواهند شد و به دلیل این برهم‌کنش فشار سیستم نیز تغییر خواهد کرد.

مثال و حل تمرین

حال که با قانون دالتون و روابط مسلط بر آن آشنا شدیم، می‌خواهم تعدادی مثال را بررسی کنیم و در هر مورد پاسخ تشریحی آن را نیز خواهیم آورد. در ادامه به مرور تعدادی تمرین چند‌گزینه‌ای می‌پردازیم.

مثال

در این بخش تعدادی مثال پیرامون قانون دالتون را به همراه پاسخ تشریحی آن‌ها مشاهده می‌کنید. توجه به پاسخ‌های تشریحی در پاسخ‌گویی به سوال‌های مشابه کمک‌کننده است.

مثال اول

مخلوطی از گاز هیدروژن و اکسیژن دارای فشار کلی برابر با ۱٫۵ اتمسفر روی دیواره‌های محفظه نگهدارنده خود هستند. در صورتی که فشار جزئی گاز هیدروژن برابر با ۱ اتمسفر باشد، کسر مولی اکسیژن را در این مخلوط به دست آورید.

پاسخ

ابتدا باید به کمک قانون دالتون، فشار جزئی گاز اکسیژن را به دست آوریم. این کار را به‌صورت زیر انجام می‌دهیم.

$$P_{total} = P_{Hydrogen} + P_{Oxygen }$$

$$1.5 = 1+ P_{Oxygen }$$

$$P_{Oxygen} = 0.5\; atm$$

با در دست داشتن فشار جزئی اکسیژن و فشار کل مخلوط، می‌توانیم کسر مولی اکسیژن را به‌صورت زیر به دست بیاوریم.

$$X_{Oxygen} = \frac{P_{Oxygen}}{P_{total}} = \frac{0.5}{1.5} = 0.33$$

همان‌طور که مشاهده می‌کنید کسر مولی گاز اکسیژن در این مخلوط برابر با ۰٫۳۳ است.

مثال دوم

نمونه‌ای از گاز $$A$$ در سیستمی بسته و در حضور آب تبخیر می‌شود. در صورتی که فشار کل سیستم برابر با ۷۸۰ تور و فشار بخار آب برابر با ۱ اتمسفر باشد، فشار جزئی گاز $$A$$ را به دست آورید.

پاسخ

ابتدا باید فشار بخار آب را به واحد اتمسفر تبدیل کنیم تا تمامی واحدها یکسان باشند.

$$P_{H_2O}= 780\; torr=1.03 \;atm$$

با توجه به اینکه فشار کل سیستم برابر با مجموع فشارهای جزئی است، از تفاضل فشار کل و فشار بخار آب، می‌توانیم مقدار فشار جزئی گاز $$A$$ را به دست بیاوریم.

$$P_A=1.03\; atm- 1\; atm=0.03 \;atm$$

مثال سوم

۲۴ لیتر از گاز نیتروژن در فشار ۱ اتمسفر و ۱۲ لیتر از گاز اکسیژن در همان فشار را به محفظه‌ای ۱۰ لیتری در دمای ۲۷۳ کلوین وارد می‌کنیم. ابتدا فشار جزئی گاز نیتروژن و گاز اکسیژن را پیدا کنید و سپس فشار کل سیستم را به دست آورید.

پاسخ

با توجه به اینکه فشار و حجم هر کدام از گازها را داریم، ابتدا تعداد مول‌های گاز اکسیژن و نیتروژن را به دست می‌آوریم.

$$moles_{Oxygen }= (12\;L\times1atm)/(0.08206\;\frac{atm.L}{mol.K} \times 273\;K) = 0.536\; mol$$

$$moles_{Nitrogen }= (24\;L\times1atm)/(0.08206\;\frac{atm.L}{mol.K} \times 273\;K) = 1.07\; mol$$

تعداد مول‌های نیتروژن و اکسیژن را با یکدیگر جمع می‌بندیم تا تعداد کل مول‌های موجود در این سیستم را به دست آوریم.

$$n_{total}= 0.536\; mol_{Oxygen}+1.07 \;mol_{Nitrogen}=1.61 \;moles$$

از تعداد مول‌های کلی سیستم برای به دست آوردن فشار کل بهره می‌بریم.

$$P_{total}=((1.61\; mol)\times(0.08206\frac{atm.L }{ mol. K})\times(273 \;K))/(10.0 \;L)=3.61\; atm$$

بنابراین فشار کل سیستم برابر با ۳٫۶۱ اتسفر است و می‌توان از آن برای محاسبه فشار جزئی هر گاز استفاده کرد.

\;$$P_{Oxygen}=(3.61\; atm)\times(0.536 \;mol_{Oxygen}/1.61 \;mol_{total})=1.20 \:atm$$

\;$$P_{Nitrogen}=(3.61\; atm)\times(1.07 \;mol_{Nitrogen}/1.61 \;mol_{total})=2.41\:atm$$

از آن‌جا که مجموع فشارهای جزئی در هر سیستم برابر با فشار کل است، بعد از محاسبه یکی از فشارهای جزئی، می‌توان از تفاضل آن با فشار کل، فشار جزء دیگر را مانند زیر به دست آورد.

$$P_{Nitrogen}=3.61 \;atm_{total}-1.20 \;atm_{Oxygen}=2.41 \;atm$$

مثال چهارم

گاز فلوئور در محفظه‌ای ۵ لیتری با دمای ۲۵ درجه سانتی‌گراد و فشار ۲ اتمسفر قرار دارد. مقدار مشخصی از گاز هیدروژن با فشار جزئی ۰٫۵ اتمسفر به آن افزوده می‌شود. کسر مولی فلوئور در این مخلوط را به دست آورید.

پاسخ

ابتدا فشار کل این سیستم را به‌صورت زیر به دست می‌آوریم.

$$2\; atm_{Flourine}+.5 \;atm_{Hydrogen}=2.5\; atm_{total}$$

با داشتن فشار کل سیستم، می‌توان کسر مولی گاز فلوئور را محاسبه کرد.

$$X_{Flourine}= \frac{0.5\;atm_{Flourine}}{2.5\;atm_{total}}=0.2$$

مثال پنجم

محفظه‌ای با ۳۲ گرم از گاز اکسیژن و ۱۲ گرم از گاز هلیوم پر شده است. فشار کلی این سیستم برابر با ۴ اتمسفر است. فشار جزئی هر یک از گازهای موجود را به دست آورید.

پاسخ

از آن‌جا که در سوال جرم هر گاز داده شده است، باید آن را تبدیل به تعداد مول کنیم. این کار را به کمک جرم مولکولی هر کدام انجام می‌دهیم.

$$mol_{O_2}=\frac{32\;g}{32.00\;g/mol}=1\;mol$$

$$mol_{He}=\frac{12\;g}{4\;g/mol}=3\;mol$$

با داشتن تعداد مول‌های هر جزء، می‌توانیم تعداد مول‌های موجود در سیستم را به‌صورت زیر به دست آوریم.

$$mol_{Total}=1\;mol_{O_2}+3\;mol_{He}=4\;mol$$

حال با توجه به اطلاعاتی که در دست داریم، کسر مولی گاز اکسیژن و هلیوم را محاسبه می‌کنیم.

$$X_{O_2}=\frac{1\;mol}{4\;mol}=0.75\;mol$$

$$X_{He}=\frac{3\;mol}{4\;mol}=0.75\;mol$$

در نهایت نیز با توجه به اینکه کسر مولی هر گاز و فشار کل را داریم، فشار جزئی آن‌ها را به‌صورت زیر به دست می‌آوریم.

$$P_{O_2}=0.25\times4\;atm=1\;atm$$

$$P_{He}=0.75\times4\;atm=3\;atm$$

مثال ششم

در مخلوطی گاز متان و اکسیژن به مقدار برابر وجود دارند و آن‌ها را وارد محفظه‌ای با دمای ۲۵ درجه سانتی‌گراد می‌کنیم. نسبت فشار اکسیژن به فشار کل سیستم را به دست آورید.

پاسخ

به توجه به رابطه فشارهای جزئی می‌توانیم تساوی زیر را برای اجزای این واکنش بنویسیم.

$$\frac{P_{O_2}}{P_{total}}=\frac{n_{O_2}}{n_{O_2}+n_{CH_4}}$$

از آن‌جا که جرم هر گاز را نداریم اما مقدار آن‌ها با یکدیگر برابر است، از $$w$$ برای نشان دادن استفاده می‌کنیم و می‌توانیم رابطه زیر را برای تعدادی مول‌های هر کدام از آن‌ها بنویسیم که عدد مخرج، جرم مولکولی آن‌ها است.

$${n_{O_2}}=\frac{w\;g}{32\;g/mol}$$

$${n_{CH_4}}=\frac{w\;g}{16\;g/mol}$$

با جای‌گذاری مقادیر بالا و ساده‌سازی به مقدار زیر می‌رسیم.

$$\frac{P_{O_2}}{P_{total}}=\frac{1}{3}$$

مثال هفتم

مخلوطی متشکل از ۷۰٫۶ گرم گاز اکسیژن و ۱۶۷٫۵ گرم گاز نئون در محفظه‌ای وجود دارد. در صورتی که فشار سیستم در این محفظه برابر با ۲۵ بار باشد، فشار جزئی گاز اکسیژن و نئون را به دست آورید. (جرم اتمی اکسیژن برابر با ۱۶ گرم بر مول و جرم اتمی نئون برابر با ۲۰٫۲ گرم بر مول است.)

پاسخ

از آن‌جا که جرم هر گاز را داریم، می‌توانیم تعداد مول‌های آن‌ها را نیز محاسبه کنیم. توجه داشته باشید که اکسیژن به شکل $$O_2$$ وجود دارد و باید جرم اتمی آن را ۲ برابر کرد.

$${n_{O_2}}=\frac{70.6\;g}{32\;g/mol}=2.21\;mol$$

$${n_{Ne}}=\frac{167.5\;g}{20.2\;g/mol}=8.29\;mol$$

از مجموع آن‌ها، تعداد کل مول‌های سیستم را به دست می‌آوریم تا از آن مقدار کسر مولی هر گاز را محاسبه کنیم.

$${n_{total}}=2.21\;mol_{O_2}+8.29\;mol _{Ne}=10.49\;mol_{total}$$

سپس کسر مولی نئون را به‌صورت زیر به دست می‌آوریم.

 $${X_{Ne}}=\frac{8.29}{10.49}=0.789$$

در اینجا کسر مولی اکسیژن را به دست نمی‌آوریم و برای داشتن فشار جزئی آن از روش دیگری استفاده می‌کنیم. سپس از ضرب کسر مولی نئون در فشار کل سیستم می‌توان فشار جزئی آن را به دست آورد.

$$P_{Ne }=X_{Ne}\times P_{total}=0.789\times25\;bar=19.7\;bar$$

حال فشار جزئی نئون و فشار کل سیستم را داریم. از آن‌جا که در این مخلوط تنها دو گاز وجود دارند، از تفاضل فشار کل و فشار جزئی نئون، فشار جزئی اکسیژن را به دست می‌آوریم.

$$P_{O_2 }=25\; bar − 19.7 \;bar = 5.3 \;bar$$

حل تمرین

حال که تعدادی مثال را بررسی کردیم، در این بخش به مرور چند تمرین چند گزینه‌ای می‌پردازیم.

             

سوالات متدوال

حال که می‌دانیم قانون دالتون چیست و چگونه می‌توان از آن استفاده کرد، در این بخش می‌خواهیم به تعدادی از مهم‌تریم و پرتکرارترین سوال‌های موجود پیرامون آن پاسخ دهیم.

قانون دالتون به چه معناست؟

این قانون بیان می‌کند که فشار کلی حاصل از مخلوطی از گازها برابر با مجموع فشارهای جزئی هر کدام از آن‌ها است.

فشار جزئی چیست؟

فشار حاصل از مخلوطی از گازها در دمایی خاص برابر با مجموع فشارهای هر کدام از آن‌ها در حالتی است که جداگانه حضور داشته باشند. به فشار هر گاز در حالت مجزا، فشار جزئی آن گفته می‌شود.

از چه واحدهایی برای بیان فشار جزئی در قانون دالتون استفاده می‌شود؟

برای بیان فشارهای جزئی از واحدهای متداول فشار مانند پاسکال و اتمسفر استفاده می‌شود.

در مخلوط گازها، فشار جزئی هر گاز به چه چیزی وابسته است؟

فشا جزئی یک گاز در مخلوطی از گازها به کسر مولی آن گاز بستگی دارد.

واحد کسر مولی چیست؟

کسر مولی کمیتی بدون واحد است.

جمع‌بندی

هدف از این مطلب مجله فرادرس آشنایی با قانون دالتون و رابطه آن با فشارهای جزئی و کسر مولی گازها بود. برای به دست آوردن فشار جزئی گازها در یک سیستم مخلوط گازی می‌توان از روابط قانون دالتون استفاده کرد که در اینجا به آن‌ها اشاره کرده‌ایم. محاسبه فشار جزئی از این نظر اهمیت دارد که از مجموع فشارهای جزئی یک سیستم گازی به فشار کل آن دست پیدا می‌کنیم. در نهایت نیز به بررسی تعدادی مثال و تمرین چند‌ گزینه‌ای پرداخته‌ایم تا توانایی کار با روابط قانون دالتون و پاسخگویی به مسائل مرتبط با آن را پیدا کنیم.