رسم تابع در متمتیکا – آموزش گام به گام و به زبان ساده
نمودارها، بخصوص در فضای دو و سه بعُدی، به درک رفتار توابع در ریاضیات کمک ارزندهای میکنند. نرمافزارهای متعددی برای رسم نمودار توابع وجود دارد. ولی شاید هیچ یک از این گونه نرمافزارها از عهده رسم توابع پیچیده و با مختصات گوناگون بر نیاید. در این بین رسم تابع در متمتیکا بسیار ساده بوده و کدهای دستوری برای ترسیم توابع بسیار خوانا هستند. بخصوص آن که معرفی تابع در این نرمافزار، به شیوه نمادین صورت گرفته و به راحتی توسط کاربر قابل درک است. به همین دلیل این نوشتار از مجله فرادرس را به کدها و نمونه تصاویر مربوط به رسم تابع در متمتیکا اختصاص دادهایم تا کسانی که به ریاضیات و علوم تجربی و حتی محض علاقمند هستند را با دستورات ترسیم نمودار تابع آشنا کنیم.
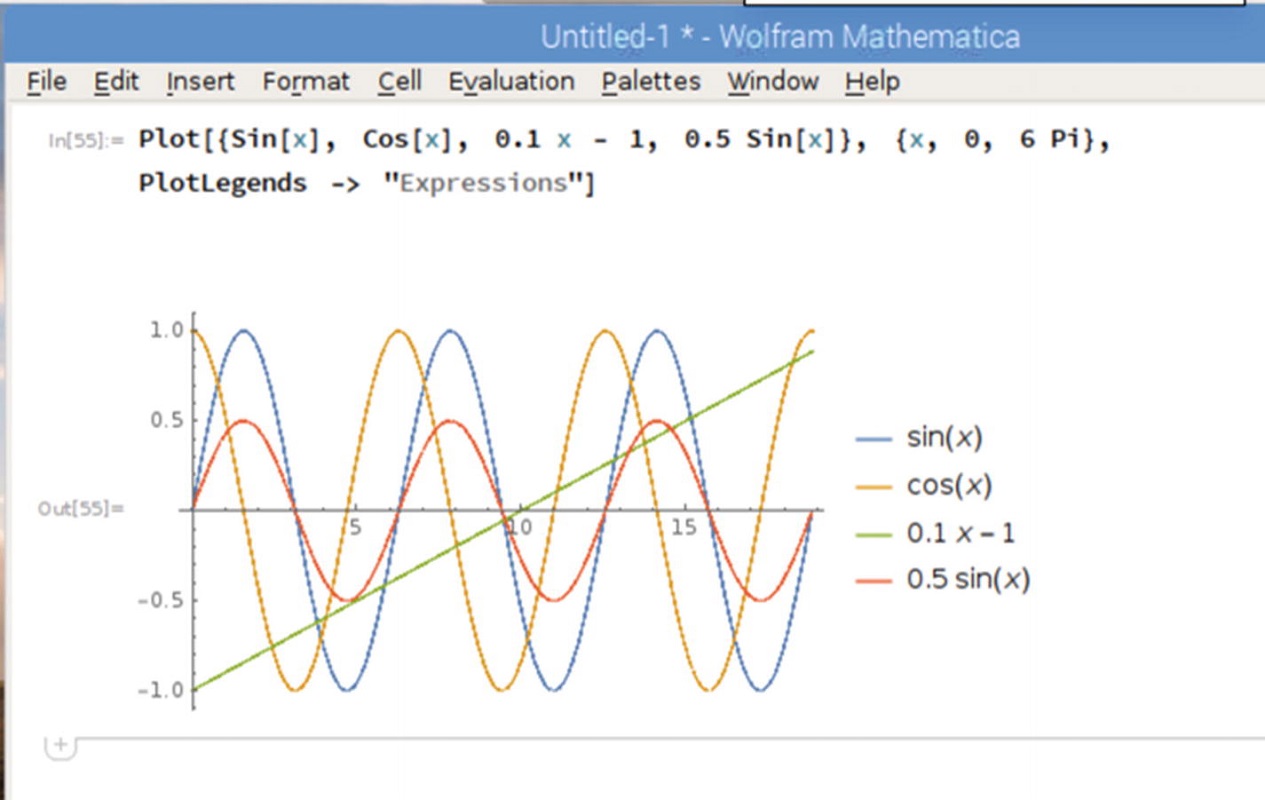
به منظور آشنایی با نرمافزار متمتیکا و همچنین بعضی از دستورات مربوط به ترسیم نمودار، نوشتارهای متمتیکا (Mathematica) چیست؟ — راهنمای شروع به کار و رسم نمودار در متمتیکا — راهنمای سریع و کاربردی را مطالعه کنید. همچنین خواندن مطالب رسم تابع — با مثال های حل شده و رسم نمودار برای دادهها — معرفی و کاربردها نیز خالی از لطف نیست.
رسم تابع در متمتیکا
«نرمافزار متمتیکا» (Mathematica) با بهرهگیری از «زبان برنامهنویسی ولفرام» (Wolfram Language)، امکان اجرای تعداد بسیار زیادی از عملیات ریاضی و آماری را دارد.
انعطاف این زبان و همچنین امکان نوشتن فرمولهای ریاضی به صورت نمادین، یکی از مهمترین وجههای این نرمافزار محسوب میشود.
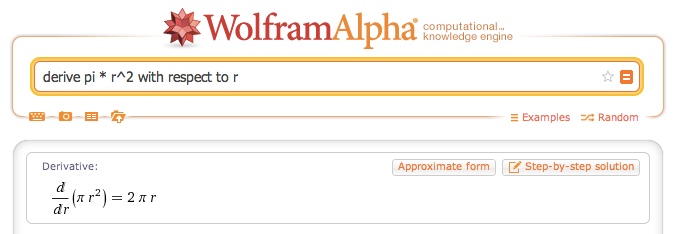
قبل از آنکه به بررسی دستورات مربوط به رسم تابع در متمتیکا بپردازیم، بهتر است برای یادآوری، مفهوم تابع را مرور کنیم. توابع در حقیقت ضوابط ریاضیاتی هستند که بین یک مجموعه با مجموعه دیگر نوشته میشوند. از جنبه دیگر میتوان رابطههایی را به عنوان زیرمجموعهای از ضرب دکارتی دو مجموعه در نظر گرفت. به این ترتیب، یک تابع، رابطهای خواهد بود که هیچ دو عضوی از آن، دارای مولفههای اول یکسان نباشند.
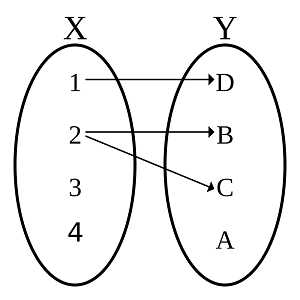
از آنجایی که توابع براساس ضرب دکارتی ساخته میشوند، میتوان آنها را در «مختصات دکارتی» (Cartesian Coordinate system) نیز نشان داد. البته مختصات دیگری نیز برای نشان دادن توابع ریاضیات به کار میروند. برای مثال میتوان به «مختصات کروی» (Polar coordinate system) یا «مختصات استوانهای» (Cylindrical coordinate System) اشاره کرد.
خوشبختانه همه این مختصات در نرمافزار متمتیکا قابل استفاده هستند. در ادامه به نحوه رسم نمودار توابع در فضای دو بُعدی در مختصات دکارتی خواهیم پرداخت. در نوشتاری دیگر به نحوه ترسیم نمودارهای سه بُعدی و مختصات کروی یا استوانهای اشاره خواهیم کرد.
رسم توابع در متمتیکا
در ابتدا با دستور ساده Plot، ترسیم تابع را آغاز میکنیم. شکل دستوری این تابع به صورت زیر است.
در رابطه بالا، نماد ضابطه تابع را مشخص کرده و ، نام متغیر درون تابع است. همچنین کران پایین و بالا برای محدوه مقادیر متغیر نیز در بخش و قابل تعیین است.
برای مثال، رسم تابع مثلثاتی (سینوس) به شکل زیر صورت میگیرد.
مشخص است که رسم تابع سینوس در بازه صفر تا انجام خواهد شد. حاصل اجرای این دستور به صورت زیر خواهد بود.
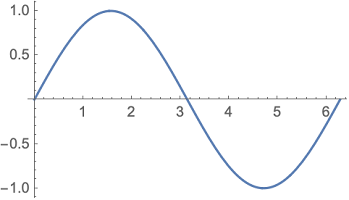
توجه داشته باشید که اگر تابع مورد نظرتان دارای نقاط منفرد (مقدار بینهایت برای تابع) باشد، متمتیکا در رسم سعی میکند، مقیاس محور عمودی را به شکلی تعیین کند که این وضعیت مشخص شود. به تصویر زیر که نمایش تابع تانژانت در بازه ۳- تا ۳ است، توجه کنید.
نمودار حاصل از اجرای دستور بالا به مانند شکل ۴ خواهد بود.
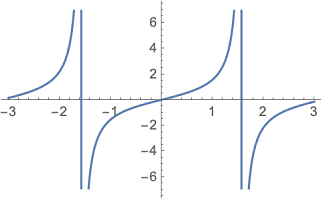
نکته: نقاط منفرد یا نقاط تکین (نقاطی که تابع در آنها بینهایت بوده یا تعریف نشده است) با پارامتر Exclusion در نمودارهای ترسیم شده با دستور Plot قابل حذف شدن هستند. به دستور زیر و تصویر ۵ توجه کنید.
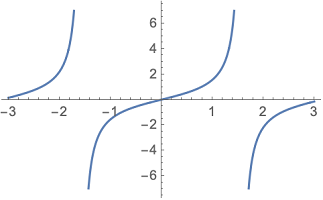
رسم همزمان چند تابع در دستور Plot
همانطور که دیدید، از دستور Plot برای رسم یک تابع کمک گرفتمی. از طرفی میتوان از تابع Plot برای ترسیم چندین تابع همزمان استفاده کرد. در این حالت همه توابع در یک مختصات، نمایش داده میشوند. در این حالت شیوه نوشتن دستور به صورت زیر خواهد بود.
برای مثال کد دستوری زیر را در نظر بگیرید.
در تصویر 6، نتیجه اجرای دستور بالا را مشاهده میکنید. واضح است که هر سه تابع Sin(x), Sin(2x) و Sin(3x) با هم در صفحه مختصات نمایش داده شدهاند. البته انتخاب رنگها برای هر یک از توابع، به صورت خودکار و توسط متمتیکا صورت گرفته است.
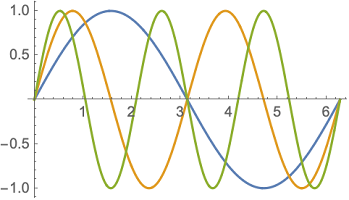
گزینههای گرافیک یا تصویری برای رسم تابع در متمتیکا
وقتی «زبان ولفرام» (Wolfram Language) یک نمودار برای شما ترسیم میکند، باید انتخابهای زیادی انجام دهد. باید تصمیم بگیرد که مقیاسها روی محورها چگونه باشد، در کجا باید از تابع نمونهبرداری شود، چگونه باید محورها ترسیم شود و غیره.
بیشتر اوقات، زبان ولفرام گزینههای بسیار خوبی را انتخاب خواهد کرد. با این حال، اگر میخواهید بهترین نتایج ممکن را برای اهداف خاص خود در رسم نمودارها بدست آورید، بهتر است زبان Wolfram را در انتخاب برخی از انتخاب ها کمک کنید.
مکانیسم کلی برای تعیین «گزینهها» (Options) در توابع زبان Wolfram وجود دارد. هر گزینه نام مشخصی دارد. به عنوان آخرین آرگومانهای تابعی مانند Plot، میتوانید دنبالهای از قوانین را به فرم name-> value برای تعیین مقادیر برای گزینههای مختلف در نظر بگیرید. البته برای گزینهای که مقدار پارامتر تعیین نشدهای داشته باشد، مقدار «پیش فرض» (Default) در نظر گرفته میشود.
به شکل تعیین پارامتر یا گزینه در دستور Plot که در ادامه دیده میشود، توجه کنید.
مشخص است که دستوری مانند Plot گزینههای زیادی دارد که لازم است توسط کاربر تنظیم شود. معمولاً باید حداکثر از دو یا سه مورد از گزینهها استفاده کنید. اگر میخواهید یک نمودار خاص را به شکل بهینه نمایش دهید، احتمالاً باید دنبالهای از تنظیمات مختلف را برای گزینههای متفاوت امتحان کنید.
هر بار که یک نمودار تولید میکنید، میتوانید گزینههایی را نیز برای آن مشخص نمایید. در جدول زیر بعضی از گزینههای معمول برای دستور Plot را معرفی کردهایم.
جدول ۱: گزینههای دستورات Plot برای رسم تابع در متمتیکا
| نام گزینه | عملکرد | مقدار پیشفرض | توضیحات |
| AspectRatio | نسبت طول به ارتفاع محورها | 1/GoldenRatio | نسبت برابر در حالت Automatic |
| Axes | نمایش محورها | True | نمایش محور افقی و عمودی در نمودار |
| AxesLabel | نمایش عنوان محورها | None | {xlabel, ylabel} برای نمایش هر دو برچسب محورها |
| AxesOrigin | محل برخورد محورها | Automatic | مختصات نقطه برخورد محورها |
| Frame | نمایش کادر دور نمودار | False | نمایش کادری در حاشیههای نمودار |
| FrameLabel | برچسب برای کادر | None | نمایش برچسب برای کادر نمودار |
| GridLines | خطوط شبکه | None | نمایش خطوط درون محورها |
| PlotLabel | برچسب نمودار | None | تعیین عنوان نمودار |
| PlotRange | دامنه نمودار | Automatic | تعیین قسمتی از محورها برای نمایش |
| PlotPoints | تعداد نقاط | Automatic | تعداد نقاط برای رسم نمودار |
| PlotStyle | سبک نمودار | Automatic | تعیین رنگ، نوع خطوط و ... |
در ادامه به بعضی از این گزینهها هنگام رسم تابع در متمتیکا اشاره خواهیم کرد.
برای مثال در نمودار زیر، با استفاده از گزینه Frame دور نمودار، یک کادر ظاهر میشود. به تصویر ۷ توجه کنید.
$$ \large \text{Plot[Sin[x^2], {x, 0, 3}, Frame -> True ] } $$
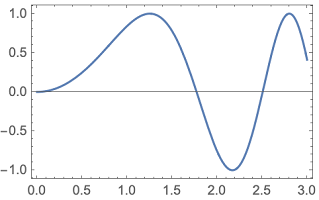
در نموداری که در تصویر ۸ مشاهده میکنید، با تغییر مقیاس محور افقی نسبت به محور عمودی، نمودار نسبت به تصویر ۷، مقداری کشیدهتر خواهد شد. واضح است که برای این کار باید از پارامتر AspectRatio استفاده کنیم. در ضمن توجه داشته باشید که به علت نسبت متفاوت بین عرض و طول صفحه نمایش، تقسیمبندی روی محور افقی کوچکتر از محور عمودی است در حالیکه نسبت انتخابی برای نمودار برابر با ۱ است.
$$ \large \text{Plot[Sin[x^2], {x, 0, 3}, AspectRatio -> 1] } $$
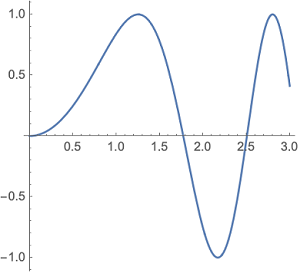
تنظیم گزینه AspectRatio کل شکل نمودار را ممکن است تغییر دهد. AspectRatio نسبت ارتفاع به عرض را مشخص میکند. همانطور که گفته شد، مقدار پیش فرض آن معکوس «نسبت طلایی» (Golden Ratio) است که ظاهراً بهترین حالت برای نمایش یک مستطیل محسوب میشود.
هنگامی که در زبان ولفرام، یک نمودار ترسیم میکنید، دستور مورد نظر سعی میکند مقیاسها و مقادیر را به شکلی تنظیم کند که فقط قسمتهای مهم از نمودار نمایش داده شوند. ولی اگر تابعی تغییرات سریع و زیادی داشته یا دارای ویژگیهای خاصی باشد، قسمتهایی که خیلی بزرگ هستند. باعث میشوند که تغییرات کوچک از دیدمان پنهان بمانند. تعیین گزینه PlotRange، میتواند دقیقاً محدودهها و مختصاتی که برایتان اهمیت بیشتری دارد را در نمودار نمایان کند. مقادیر مربوط به گزینه PlotRange طبق فهرست زیر تعیین میشوند.
- Automatic: درصد زیادی از نقاط مربوط به تابع نمایان میشوند. نقاط با اهمیت باید در نمودار ظاهر شوند. این گزینه به عنوان مقدار پیشفرض برای این گزینه تعیین شده است.
- All: همه نقاط تابع در نمودار دیده میشوند. ممکن است رسم نمودار به این شکل، نمودار زیبایی را تولید نکند.
- : تعیین محدوده پایین و بالا برای مقادیر محور عمودی.
- :تعیین حدود برای متغیر یا محور افقی و عمودی این کرانها بوسیله پرانتز مشخص میشوند.
در دستور زیر با تعیین ناحیه رسم، فقط بخشهای مثبت نمودار تابع سینوس مربع ایکس رسم شده است. واضح است که مقادیر مربوط به محور افقی در بازه ۰ تا ۳ قرار دارند.
$$ \large \text{Plot[Sin[x^2], {x, 0, 3}, PlotRange -> {0, 1.2}] }$$
در زبان ولفرام همیشه سعی میشود، توابع به صورت منحنیهای صاف ترسیم شوند. در نتیجه، در مکانهایی که تابع تغییرات شدید و زیادی دارد، زبان ولفرام از نقاط بیشتری استفاده خواهد کرد. به طور کلی، در این زبان تلاش میشود که نمونه برداری از تابع با شکل تابع بیشترین مطابقت را داشته باشد.
ولی به هر حال محدودیتهایی نیز باید وجود داشته باشد. باید تعداد نقاط نمونهبرداری شده متناهی باشند در غیر اینصورت، ممکن است هرگز شکل نمودار مشخص نشود. به نموداری تابع توجه کنید. در نقطههایی که به صفر نزدیک هستند، مقدار تابع بسیار بزرگ شده و در عمل نمیتوان آنها را نمایش داد. به این ترتیب ولفرام، بخشی که مهمتر از بقیه نقاط هستند را در نمودار نمایش خواهد داد. به تصویر ۹ توجه کنید.
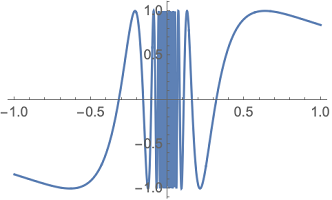
این نمودار با استفاده از کد زیر ترسیم شده است.
گاهی لازم است که هنگام رسم تابع در متمتیکا فقط تعداد محدودی از نقاط نمونهبرداری شوند، بنابراین میتوان تعداد نمونهها یا نقاط را در نزدیکی محلهای خاصی از تابع افزایش یا کاهش داد. با افزایش مقدار برای گزینه PlotPoints، میتوانید تابع خود را در محل مشخص شده، دقیقتر رسم کنید. مطمئناً، هرچه مقدار PlotPoints را بیشتر تنظیم کنید، برای ترسیم هر تابع، مدت زمان طولانیتری صرف خواهید کرد.
دستور زیر به رسم تابع سینک (Sinc) در بازه ۰ تا ۱۰ با استفاده از ۵۰ نقطه اختصاص دارد. نمودار رسم شده را در تصویر ۱۰ مشاهده میکنید.
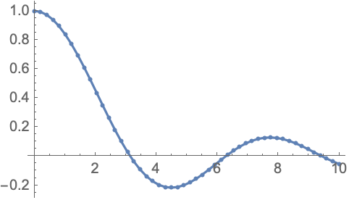
نکته: تابع سینک (غیراستاندارد شده) به صورت زیر تعریف میشود. در حقیقت این تابع، نسبت سینوس یک زاویه به خود زاویه است.
امکان دیگر برای تنظیم نحوه رسم تابع در متمتیکا استفاده از گزینه PlotStyle است. مقادیر این گزینه میتواند شامل نوع خط (Line Style)، رنگ خطوط (Color) و یا ترکیبی از آنها باشد. به تصویر ۱۱ توجه کنید. نمودار سینوس و کسینوس بوسیله رنگهای متفاوت در دستور Plot دیده میشوند. کد دستوری برای انجام این کار به صورت زیر است.
$$ \large \text{ Plot[{Sin[x^2], Cos[x^2]}, {x, 0, 3}, PlotStyle -> {Red, Blue}] } $$
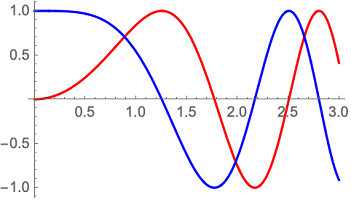
حتی میتوان از دو مشخصه به صورت ترکیبی در گزینه PlotStyle استفاده کرد. دستور زیر برای تمایز بین توابع رسم شده در نمودار، هم از رنگ و هم از نوع خط (کلفت-Thick) استفاده کرده است. کد مربوطه به صورت زیر نوشته میشود.
$$ \large \text {Plot[{Sin[x^2], Cos[x^2]}, {x, 0, 3}, PlotStyle -> {Red, {Blue, Thick}}] } $$
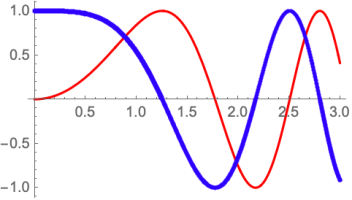
همچنین نوع خط ترسیم شده برای تابع در نمودار نیز در این گزینه نهفته است. دستور زیر را در نظر بگیرید. مقدار PlotStyle با Dashed (خط چین) تعیین شده است. بنابراین برای ترسیم خطوط نمودار از خط چین استفاده خواهد شد. نتیجه اجرای دستور زیر در تصویر ۱۳ قابل مشاهده است.
$$ \large \text{Plot[Sin[x^2], {x, 0, 3}, PlotStyle -> Dashed] } $$
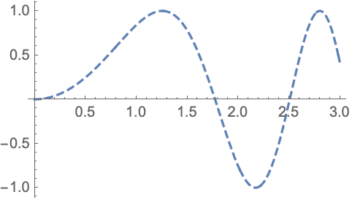
خلاصه و جمعبندی
همانطور که در متن خواندید، رسم تابع در متمتیکا به راحتی و با فراگیری چند دستور، امکانپذیر است. حسن استفاده از متمتیکا برای رسم توابع ریاضیاتی، آن است که از نمادها برای مشخص کردن تابع استفاده میشود. به این ترتیب کاربر بدون آنکه فرمول یا نقطهدهی انجام دهد، تابع دلخواه خود را در بازهای که مورد احتیاج است، رسم خواهد کرد. به علاوه رسم توابع به صورت ترکیبی و زیبایی نمایش نمودار توابع، از مزایایی است که در کمتر نرمافزاری دیده میشود.
از طرفی دستوراتی نیز برای توابع چند ضابطهای و همچنین ترسیم چندین تابع در یک مختصات وجود دارد که به امر تحلیل چند متغیره کمک شایانی میکند. این خصوصیات متمتیکا را به نرمافزاری کاملا متمایز برای محاسبات ریاضی برای رشتههای مختلف علوم تبدیل کرده است.












