ثابت اویلر ماسکرونی (Euler–Mascheroni) — به زبان ساده

مقادیر ثابت (Constant) در علوم مختلف به عنوان ابزاری برای توجیه نسبت‌ها به کار گرفته می‌شوند. مثلا در فیزیک، ثابت گازها، یا در شیمی عدد آووگادرو  مقادیر ثابتی هستند که در بسیار از محاسبات مربوط به آن رشته به کار می‌روند. در ریاضیات نیز برای مثال عدد پی ($$\pi$$) یک ثابت محسوب شده که نسبت محیط دایره به قطر آن را نشان می‌دهد. از آنجایی که این نسبت‌ها، مقادیری با تعداد اعشار زیاد بوده و اکثراً در مجموعه اعداد گنگ قرار دارند، گاهی آن‌ها را با دقت کمتری (مثلا ۵ رقم اعشار) نشان داده و در محاسبات به کار می‌برند. یکی از ثابت‌های جالب در حوزه علوم ریاضی، ثابت ثابت اویلر ماسکرونی (Euler–Mascheroni) است که گاهی به آن ثابت اویلر نیز می‌گویند که در این نوشتار به آن پرداخته و خصوصیات آن را مورد بحث قرار می‌دهیم.

برای آشنایی بیشتر با ثابت‌های دیگر در ریاضیات می‌توانید مطلب نسبت طلایی — به زبان ساده و دنباله فیبوناچی – به زبان ساده را مطالعه کنید. همچنین خواندن عدد پی چگونه کشف شد؟ — ریاضیات به زبان ساده و عدد اویلر یا نپر – به زبان ساده نیز خالی از لطف نیست.

ثابت اویلر ماسکرونی

یک ثابت در آنالیز و تئوری اعداد، ثابت اویلر ماسکرونی است که معمولا با حرف کوچک لاتین گاما ($$\gamma$$) نشان داده می‌شود.

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

به طور رسمی تعریف این عدد به صورت حد یک عبارت لگاریتمی است.

$$\large {\displaystyle{\gamma =\lim _{n\to \infty }\left(-\ln n+\sum _{k=1}^{n}{\frac {1}{k}}\right)}}$$

رابطه ۱

که می‌توان آن را به صورت یک انتگرال به شکل زیر نیز نوشت:

$$\large {\displaystyle \gamma =\int _{1}^{\infty }\left(-{\frac {1}{x}}+{\frac {1}{\lfloor x\rfloor }}\right)\,dx}$$

رابطه ۲

در اینجا منظور از $$\lfloor x \rfloor$$ تابع کف (Floor Function) یا همان جزء صحیح است.

مقدار این حد یا انتگرال با دقت ۵۰ رقم اعشار به صورت زیر است:

$$\large 0.57721566490153286060651209008240243104215933593992$$

اگر با توجه به رابطه ۱، نمودار لگاریتم طبیعی یعنی $$\ln(n)$$ و $$\sum_{k=1}^n \dfrac{1}{k}$$ را ترسیم کنیم، شکلی به مانند تصویر زیر خواهیم داشت.

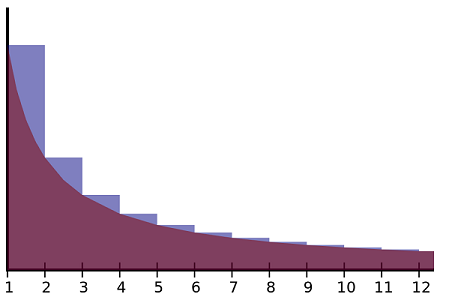
واضح است که تفاضل این دو مقدار در بی‌نهایت به ثابت اویلر، ماسکرونی میل خواهد کرد. این تفاضل‌ها بوسیله قسمت‌هایی از مستطیل‌هایی به رنگ آبی در نمودار بالا نشان داده شده‌اند.

تاریخچه ثابت اویلر ماسکرونی

این ثابت اولین بار توسط ریاضیدان سوئیسی، «لئونارد اویلر» (Leonhard Euler)، در مقاله‌ای که در سال 1734 منتشر کرد، معرفی شذ. اویلر از نمادهای C و O برای نمایش این ثابت استفاده کرد. بعدها، در سال 1790، ریاضیدان ایتالیایی، «لورنزو ماسکرونی» (Lorenzo Mascheroni) از علامت‌های A و a برای نمایش این ثابت کمک گرفت. البته نماد $$\gamma$$ در هیچ‌کدام از نوشته‌های اویلر یا ماسکرونی ظاهر نشده است، ولی ممکن است به علت ارتباط این ثابت به تابع گاما، این نوع نمایش برای آن در نظر گرفته شده باشد. برای مثال در سال ۱۸36، دمورگان (Augustus De Morgan) این ثابت را با نماد $$\gamma$$ در کتاب خود به کار برد.

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

دقت محاسباتی در سال‌های مختلف برای ثابت اویلر ماسکرونی در جدول زیر نمایش داده شده است.

کاربردهای ثابت اویلر ماسکرونی

موارد زیر به حوزه‌هایی اشاره دارد که با ثابت اویلر-ماسکرونی در ارتباط هستند.

• محاسبات مربوط به انتگرال توابع نمایی.
• تبدیل لاپلاس لگاریتم طبیعی.
• خصوصیات و ویژگی‌های تابع توزیع گامبل.
• تابع گاما و نمایش حاصلضربی برای آن.
• محاسبه تابع دی‌گاما (Digamma).
• آنتروپی اطلاعات در توزیع‌های وایبل (Weibull) و لوی (Levy) و به طور ضمنی،  توزیع مربع کای با یک یا دو درجه آزادی.
• پاسخ مسئله جمع‌آوری کوپن!
• پاسخ معادلات بسل نوع دوم (Bessel's Equation, Second Kind).

برای مثال اگر تابع گاما (Gamma Function) را در نظر بگیریم، مشتقل اول این تابع در نقطه ۱ برابر است با قرینه ثابت اویلر. یعنی:

$$\large {\displaystyle -\gamma =\Gamma '(1)=\Psi (1)}$$

نکته: در اینجا منظور از $$\Psi$$ مشتق اول تابع گاما است که گاهی به آن دی‌گاما (digamma) نیز می‌گویند.

ثابت اویلر را به صورت انتگرال تابع نمایی نیز می‌توان نوشت. به تساوی‌های زیر توجه کنید.

$$\large {\displaystyle {\begin{aligned}\gamma &=-\int _{0}^{\infty }e^{-x}\ln x\,dx\\&=-\int _{0}^{1}\ln \left(\ln {\frac {1}{x}}\right)dx\\&=\int _{0}^{\infty }\left({\frac {1}{e^{x}-1}}-{\frac {1}{x\cdot e^{x}}}\right)dx\\&=\int _{0}^{1}\left({\frac {1}{\ln x}}+{\frac {1}{1-x}}\right)dx\\&=\int _{0}^{\infty }\left({\frac {1}{1+x^{k}}}-e^{-x}\right){\frac {dx}{x}},\quad k>0\\&=\int _{0}^{1}H_{x}\,dx\end{aligned}}}$$

در این رابطه منظور از $$H_x$$ عدد هارمونیک کسری است که به صورت زیر نوشته می‌شود.

$$\large {\displaystyle H_{x}=\psi (x+1)+\gamma}$$

مشخص است که $$\gamma$$ همان ثابت اویلر و $$\psi$$ نیز تابع دی‌گاما است. همچنین نتیجه و حاصل انتگرال‌های زیر نیز با مقدار ثابت اویلر ماسکرونی (Euler–Mascheroni) مرتبط است.

$$\large{\displaystyle {\begin{aligned}\int _{0}^{\infty }e^{-x^{2}}\ln x\,dx&=-{\frac {(\gamma +2\ln 2){\sqrt {\pi }}}{4}}\\\int _{0}^{\infty }e^{-x}\ln ^{2}x\,dx&=\gamma ^{2}+{\frac {\pi ^{2}}{6}}\end{aligned}}}$$

همچنین در جهان ارقام باینری (دو-دویی) بین تعداد صفرها و یک‌های یک عدد برمبنای ۲ رابطه زیر برقرار است. این رابطه نقش ثابت اویلر را در تصحیح خطا در مخابرات دیجیتال و انتقال داده‌ها نشان می‌دهد.

$$\large{\displaystyle \gamma =\sum _{n=1}^{\infty }{\frac {N_{1}(n)+N_{0}(n)}{2n(2n+1)}}}$$

جالب است که عدد پی ($$\pi$$) نیز با تعداد ارقام صفر و یک اعداد باینری در ارتباط است.

$$\large{\displaystyle \ln {\frac {4}{\pi }}=\sum _{n=1}^{\infty }{\frac {N_{1}(n)-N_{0}(n)}{2n(2n+1)}}}$$

در اینجا $$N_1(n)$$ تعداد ارقام ۱ در عدد باینری $$n$$ است و $$N_0(n)$$ نیز تعداد ارقام صفر را در این عدد نشان می‌دهد.

جمع‌‌بندی و خلاصه

در این نوشتار با ثابت اویلر-ماسکرونی (Euler–Mascheroni) آشنا شدیم و نقش آن را در حوزه‌های دیگر ریاضی مرور کردیم. البته این ثابت علاوه بر ریاضی، در علوم دیگر مانند آمار و فیزیک نیز کاربرد دارد. حتی در رمز‌نگاری و تصحیح خطا نیز می‌توان از ثابت اویلر ماسکرونی (Euler–Mascheroni) استفاده کرد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش‌های آمار و احتمالات
• نسبت طلایی — به زبان ساده
• نماد انتگرال – با سرگذشت جالب این علامت ریاضی آشنا شوید
• سری تیلور — از صفر تا صد

^^