متغیر تصادفی و توزیع گامبل — به زبان ساده

در تئوری آمار و احتمالات، «توزیع گامبل» (Gumbel Distribution) به عنوان یکی از «توزیع‌های مقادیر حدی» (Extreme Value Distribution) محسوب می‌شود. متغیر تصادفی و توزیع گامبل برای توصیف رفتار مقدارهای حداکثر تعدادی از نمونه‌های تصادفی به کار می‌رود. برای مثال اگر ارتفاع آب یک رودخانه را در نظر بگیریم، متغیر تصادفی حداکثر ارتفاع آب رودخانه در هر سال‌ می‌‌تواند دارای توزیع گامبل باشد. بنابراین اطلاع از توزیع احتمال متغیر تصادفی گامبل به شناخت پدیده‌های تصادفی که مربوط به حداکثر میزان‌هایی مانند شدت زلزله، ارتفاع سیلاب و دیگر بلایای طبیعی است، کمک خواهد کرد.

در این نوشتار به بررسی متغیر تصادفی و توزیع گامبل می‌پردازیم و خصوصیات آن را مورد بررسی قرار می‌دهیم. برای آشنایی بیشتر با مفاهیم مربوط به توزیع‌های آماری بهتر است مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کنید. همچنین مطالعه توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس نیز خالی از لطف نیست.

متغیر تصادفی و توزیع گامبل

توزیع گامبل را به عنوان شکل خاصی از توزیع‌های مقادیر حدی می‌شناسند. گاهی به توزیع گامبل، «توزیع لگاریتم وایبل» (Log-Weibull) یا توزیع نمایی دوتایی (Double Exponential Distribution) نیز گفته می‌شود.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

علت نام‌گذاری این توزیع به نام گامبل، کارها و تحقیقاتی است که «امیل گامبل» (Emil Julius Gumbel) دانشمند و ریاضی‌دان آلمانی در سال‌های ابتدای قرن بیستم در آمریکا روی این توزیع انجام داد.

تابع احتمال و توزیع گامبل

متغیر تصادفی $$X$$ را دارای توزیع گامبل می‌گویند اگر تابع توزیع احتمال تجمعی آن به صورت زیر نوشته شود:

$$\large F(x;\mu ,\beta )=e^{{-e^{{-(x-\mu )/\beta }}}} x\in R$$

همانطور که دیده شد، این توزیع با پارامترهای مرکزی $$\mu$$ و مقیاس $$\beta$$ شناخته می‌شود. پارامتر مرکزی $$\mu$$ به عنوان مقدار نما و پارامتر مقیاس $$\beta$$ نیز مثبت اختیار می‌شود. به این ترتیب می‌نویسند $$X\sim Gumbel(\mu,\beta)$$ و می‌خوانند $$X$$ دارای توزیع گامبل با پارامترهای مرکزی $$\mu$$ و مقیاس $$\beta$$‌ است.

تابع چگالی احتمال برای متغیر تصادفی گامبل به صورت زیر نوشته می‌شود.

$$\large f_X(x)={\displaystyle {\frac {1}{\beta }}e^{-(z+e^{-z})}}$$

که در آن داریم $$ z=\frac {x-\mu }{\beta }$$ است.

اغلب فرم استاندارد تابع توزیع احتمال متغیر تصادفی را به صورت زیر نشان می‌دهند که در آن پارامتر مرکزی برابر با $$\mu=0$$ و پارامتر مقیاس نیز $$\beta=1$$ در نظر گرفته می‌شود. در این صورت تابع توزیع احتمال به صورت زیر در خواهد آمد.

$$\large F(x)=e^{{-e^{{(-x)}}}}\,$$

در این حالت، نما صفر بوده و میانه نیز برابر است با $$-ln(ln(2))\approx 0.3665$$

تابع چگالی احتمال برای متغیر تصادفی گامبل استاندارد نیز به صورت زیر نوشته می‌شود.

$$\large f(x)=e^{{-(x+e^{{-x}})}}$$

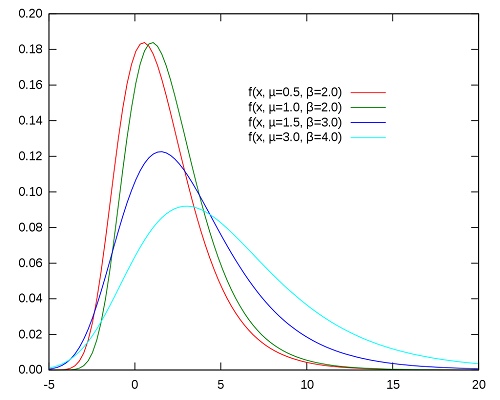
نمودار تابع چگالی و توزیع این متغیر تصادفی در تصویرهای زیر قابل مشاهده است. مشخص است که این توزیع دارای چولگی به سمت راست (Right Skewed) است. واضح است که با افزایش مقدار پارامتر $$\beta$$‌ میزان چولگی نمودار تابع چگالی نیز بیشتر می‌شود.

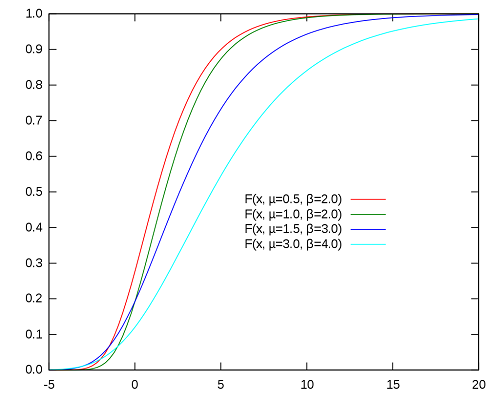
خصوصیات متغیر تصادفی گامبل

اگر متغیر تصادفی $$X$$ دارای توزیع گامبل باشد، امید ریاضی آن توسط رابطه زیر قابل محاسبه است.

$$\large E(X)=\mu+\beta\gamma$$

توجه داشته باشید که ثابت $$\gamma$$ در اینجا همان ثابت اویلر-ماسکرونی (Euler-Mascheroni Constant) است که برابر با $$\gamma\approx 0.5772$$.

به همین ترتیب میانه نیز برابر است با:

$$\large \mu-\beta\ln(\ln 2)$$

از طرفی واریانس برای این متغیر تصادفی به صورت زیر محاسبه می‌شود:

$$\large Var(X) = \dfrac{\pi^2}{6}\beta^2$$

ارتباط توزیع گامبل با توزیع‌های دیگر

فرض کنید متغیر تصادفی $$Y$$ دارای توزیع نمایی (Exponential Distribution) (با میانگین $$\lambda=1$$) باشد، آنگاه قرینه لگاریتم آن دارای توزیع گامبل استاندارد است.

$$\large Y \sim E(1) \rightarrow -\ln(Y)\sim Gumbel (0,1)$$

اگر $$X$$ و $$Y$$ دو متغیر تصادفی باشند که هر کدام دارای توزیع گامبل با پارامترهای $$\alpha$$ و $$\beta$$ باشند آنگاه تفاصل آن‌ها، دارای توزیع لجستیک خواهد بود.

$$\large X, Y \sim Gumbel(\alpha,\beta) \rightarrow X-Y \sim Logistic (0,\beta)$$

به این ترتیب می‌توان نشان داد که در شرایط زیر توزیع تفاضل دو متغیر تصادفی گامبل، یک توزیع لجستیک خواهد بود.

$$\large\begin{cases}X \sim Gumbel(\alpha_x,\beta) & \\Y \sim Gumbel(\alpha_y,\beta)&\end{cases} \rightarrow X-Y\sim Logistic(\alpha_x-\alpha_y,\beta)$$

کاربردهای توزیع گامبل

در بررسی‌هایی که گامبل روی مقدارهای حداکثر انجام داد، متوجه شد که بزرگترین مقدارهای نمونه‌های تصادفی حاصل از یک متغیر تصادفی توزیع نمایی، با افزایش اندازه نمونه، به متغیر تصادفی با توزیع گامبل نزدیکتر می‌شوند.

گامبل همچنین نشان داد که برآوردگر $$\dfrac{r}{n+1}$$ یک برآوردگر نااریب (Unbiased Estimator) حول میانه برای احتمال تجمعی وقوع یک رویداد است، به شرطی که در آن $$r$$ رتبه مقدار مشاهده شده و $$n$$ نیز تعداد کل مشاهدات باشد.

فیلم آموزش متغیرهای تصادفی پیوسته (رایگان) در فرادرس

کلیک کنید

در یادگیری ماشین، برای تولید نمونه تصادفی برای متغیرهای طبقه‌ای اغلب از متغیر تصادفی و توزیع گامبل استفاده می‌شود.

در هیدرولوژی و آبشناسی که مرتبط با دبی رودخانه و سیلاب‌ها هستند، از متغیر تصادفی و توزیع گامبل برای تجزیه و تحلیل متغیرهایی که براساس مقادیر حداکثر ماهانه و سالانه میزان بارندگی روزانه و حجم تخلیه (دبی) رودخانه استفاده می‌شود. همچنین از این توزیع به منظور برازش داده‌های پیش‌بینی دوره‌های خشکسالی استفاده‌های فراوانی می‌شود.

در آبخیز‌داری نیز، توزیع گامبل بسیار به کار می‌رود بطوری که برای بیان پیشامدهایی با مقدارهای بسیار بزرگ (کرانگین)، مناسب به نظر می‌رسد در تصویر زیر یک نمونه از برازش توزیع داده‌های مربوط به میزان حداکثر بارش در روز، بوسیله توزیع گامبل دیده می‌شود. در تصویر، دایره‌های آبی رنگ، مقادیر مشاهده شده و منحنی سفید رنگ، برازش براساس توزیع گامبل را مشخص کرده است. همچنین خطوط زرد رنگ هم فاصله اطمینان با میزان ۹۰ درصد را برای برازش نقطه‌ها نشان می‌دهند.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های مدل سازی، برازش و تخمین
• نامساوی چبیشف – کاربرد در توزیع‌های غیرنرمال
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^