نوع خاصی معادله دیفرانسیل معمولی وجود دارد که با نام معادله دیفرانسیل لژاندر شناخته میشود و در فیزیک و مهندسی کاربرد زیادی دارد. این معادله به ویژه در حل معادله لاپلاس در مختصات کروی بسیار کارساز است. در این آموزش با معادله لژاندر و توابع لژاندر آشنا میشویم.
تعاریف و معرفی
در این بخش برخی توابع و معادلههای مرتبط با لژاندر را معرفی میکنیم.
معادله لژاندر و توابع لژاندر
معادله دیفرانسیل رتبه دوم زیر به عنوان معادله لژاندر نامیده میشود:
( 1 − x 2 ) d 2 y d x 2 − 2 x d y d x + n ( n + 1 ) y = 0 n > 0 , ∣ x ∣ < 1 \large \left ( 1 - x ^ { 2 } \right ) \frac { d ^ { 2 } y } { d x ^ { 2 } } - 2 x \frac { d y } { d x } + n ( n + 1 ) y = 0 \quad n > 0 , \quad | x | < 1 ( 1 − x 2 ) d x 2 d 2 y − 2 x d x d y + n ( n + 1 ) y = 0 n > 0 , ∣ x ∣ < 1
جواب عمومی این معادله تابعی از دو تابع لژاندر به فرم زیر است:
y = A P n ( x ) + B Q n ( x ) ∣ x ∣ < 1 \large y = A P _ { n } ( x ) + B Q _ { n } ( x ) \quad | x | < 1 y = A P n ( x ) + B Q n ( x ) ∣ x ∣ < 1
که در آن، P n ( x ) = 1 2 n n ! d n d x n ( x 2 − 1 ) n P _ n ( x ) = \frac { 1 } { 2 ^ n n ! } \frac { d ^ n } { d x ^ n } ( x ^ 2 - 1 ) ^ n P n ( x ) = 2 n n ! 1 d x n d n ( x 2 − 1 ) n Q n ( x ) = 1 2 P n ( x ) ln 1 + x 1 − x Q _ n ( x ) = \frac { 1 } { 2} P _ n ( x ) \ln \frac { 1 + x } { 1 - x } Q n ( x ) = 2 1 P n ( x ) ln 1 − x 1 + x
معادله دیفرانسیل وابسته لژاندر
معادله دیفرانسیل وابسته لژاندر به صورت زیر است:
( 1 − x 2 ) d 2 y d x 2 − 2 x d y d x + [ n ( n + 1 ) − m 2 1 − x 2 ] y = 0 \large \left ( 1 - x ^ { 2 } \right ) \frac { d ^ { 2 } y } { d x ^ { 2 } } - 2 x \frac { d y } { d x } + \left [ n ( n + 1 ) - \frac { m ^ { 2 } } { 1 - x^ { 2 } } \right ] y = 0 ( 1 − x 2 ) d x 2 d 2 y − 2 x d x d y + [ n ( n + 1 ) − 1 − x 2 m 2 ] y = 0
اگر m = 0 m = 0 m = 0
جواب عمومی معادله دیفرانسیل لژاندر به صورت زیر است:
y = A P n m ( x ) + B Q n m ( x ) \large y = A P _ n ^ m ( x ) + B Q _ n ^ m ( x ) y = A P n m ( x ) + B Q n m ( x )
که در آن، P n m ( x ) P _ n ^ m ( x ) P n m ( x ) Q n m ( x ) Q _ n ^ m ( x ) Q n m ( x )
P n m ( x ) = ( 1 − x 2 ) m / 2 d m d x m P n ( x ) Q n m ( x ) = ( 1 − x 2 ) m / 2 d m d x m Q n ( x ) \large \begin {array} { l } { \mathbf { P } _ { n } ^ { m } ( x ) = \left ( 1 - x ^ { 2 } \right ) ^ { m / 2 } \frac { d ^ { m } } { d x ^ { m } } P _ { n } ( x ) } \\ { Q _ { n } ^ { m } ( x ) = \left ( 1 - x ^ { 2 } \right ) ^ { m / 2 } \frac { d ^ { m } } { d x ^{ m } } Q _ { n } ( x ) } \end {array} P n m ( x ) = ( 1 − x 2 ) m /2 d x m d m P n ( x ) Q n m ( x ) = ( 1 − x 2 ) m /2 d x m d m Q n ( x )
معادله لژاندر و جوابهای آن
معادله دیفرانسیل لژاندر به صورت زیر است:
( 1 − x 2 ) d 2 y d x 2 − 2 x d y d x + n ( n + 1 ) y = 0 n > 0 , ∣ x ∣ < 1 \large \left ( 1 - x ^ { 2 } \right ) \frac { d ^ { 2 } y } { d x ^ { 2 } } - 2 x \frac { d y } { d x } + n ( n + 1 ) y = 0 \quad n > 0 , \quad | x | < 1 ( 1 − x 2 ) d x 2 d 2 y − 2 x d x d y + n ( n + 1 ) y = 0 n > 0 , ∣ x ∣ < 1
یا به طور معادل:
d d x [ ( 1 − x 2 ) d y d x ] + n ( n + 1 ) y = 0 n > 0 , ∣ x ∣ < 1 \large \frac { d } { d x } \left [ \left ( 1 - x ^ { 2 } \right ) \frac { d y } { d x } \right ] + n ( n + 1 ) y = 0 \quad n > 0 , \quad | x | < 1 d x d [ ( 1 − x 2 ) d x d y ] + n ( n + 1 ) y = 0 n > 0 , ∣ x ∣ < 1
جوابهای این معادله، توابع لژاندر مرتبه n n n
y = A P n ( x ) + B Q n ( x ) ∣ x ∣ < 1 \large y = A P _ n ( x ) + B Q _ n ( x ) \quad \quad | x | < 1 y = A P n ( x ) + B Q n ( x ) ∣ x ∣ < 1
که در آن، P n ( x ) P _ n ( x ) P n ( x ) Q n ( x ) Q _ n ( x ) Q n ( x ) n n n
اگر n = 0 , 1 , 2 , 3 , … n =0, 1 , 2 , 3 , \ldots n = 0 , 1 , 2 , 3 , … P n ( x ) P _ n ( x ) P n ( x )
P n ( x ) = 1 2 n n ! d n d x n ( x 2 − 1 ) n \large \mathbf { P } _ { n } ( x ) = \frac { 1 } { 2 ^ { n } n ! } \frac { d ^ { n } } { d x ^ { n } } \left ( x ^ { 2 } - 1 \right ) ^ { n } P n ( x ) = 2 n n ! 1 d x n d n ( x 2 − 1 ) n
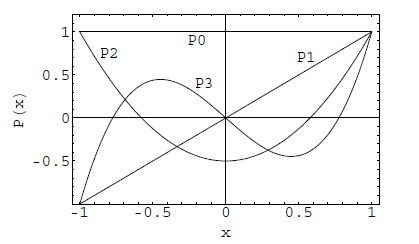
توابع لژاندر نوع اول P n ( x ) P _ n ( x ) P n ( x ) Q n ( x ) Q _ n ( x ) Q n ( x ) n = 0 , 1 , 2 , 3 n = 0 , 1 , 2 , 3 n = 0 , 1 , 2 , 3
P ( x ) P(x) P ( x ) شکل ۱: تابع لژاندر نوع اول (P ( x ) P(x) P ( x ) Q ( x ) Q(x) Q ( x ) شکل ۲: تابع لژاندر نوع دوم (Q ( x ) Q(x) Q ( x ) چند چندجملهای اول لژاندر به صورت زیر هستند:
P 0 ( x ) = 1 P 3 ( x ) = 1 2 ( 5 x 3 − 3 x ) P 1 ( x ) = x P 3 ( x ) = 1 8 ( 35 x 4 − 30 x 2 + 3 ) P 2 ( x ) = 1 2 ( 3 x 2 − 1 ) P 3 ( x ) = 1 8 ( 63 x 5 − 70 x 3 + 15 x ) \begin {array} {ll} { \mathrm { P } _ { 0 } ( x ) = 1 } & { \mathrm { P } _ { 3 }( x ) = \frac { 1 } { 2 } \left ( 5 x ^ { 3 } - 3 x \right ) } \\ { \mathrm { P } _ { 1 } ( x ) = x } & { \mathrm { P } _ { 3 } ( x ) = \frac { 1 } { 8 } \left ( 3 5 x ^ { 4 } - 3 0 x ^ { 2 } + 3 \right ) } \\ { \mathrm { P } _ { 2 } ( x ) = \frac { 1 } { 2 } \left ( 3 x ^ { 2 } - 1 \right ) } & { \mathrm { P } _ { 3 } ( x ) = \frac { 1 } { 8 } \left ( 6 3 x ^ { 5 } - 7 0 x ^ { 3 } + 1 5 x \right ) } \end {array} P 0 ( x ) = 1 P 1 ( x ) = x P 2 ( x ) = 2 1 ( 3 x 2 − 1 ) P 3 ( x ) = 2 1 ( 5 x 3 − 3 x ) P 3 ( x ) = 8 1 ( 35 x 4 − 30 x 2 + 3 ) P 3 ( x ) = 8 1 ( 63 x 5 − 70 x 3 + 15 x )
فرمول بازگشتی چندجملهای به صورت زیر است:
P n + 1 ( x ) = 2 n + 1 n + 1 x P n ( x ) − n n + 1 P n − 1 ( x ) P n + 1 ′ ( x ) − P n − 1 ′ ( x ) = ( 2 n + 2 ) P n ( x ) \large \begin {aligned} & \mathbf { P } _ { n + 1 } ( x ) = \frac { 2 n + 1 } { n + 1 } x P _ { n } ( x ) - \frac { n } { n + 1 } P _ { n - 1 } ( x ) \\ & \mathbf { P } _ { n + 1 } ^ { \prime } ( x ) -\mathbf { P } _ { n - 1 } ^ { \prime } ( x ) = ( 2 n + 2 ) \mathbf { P } _ { n } ( x ) \end {aligned} P n + 1 ( x ) = n + 1 2 n + 1 x P n ( x ) − n + 1 n P n − 1 ( x ) P n + 1 ′ ( x ) − P n − 1 ′ ( x ) = ( 2 n + 2 ) P n ( x )
و از آن در به دست آوردن چندجملهایهای مرتبه بالاتر استفاده میشود. در همه موارد P n ( 1 ) = 1 P _ { n } ( 1 ) = 1 P n ( 1 ) = 1 P n ( − 1 ) = ( − 1 ) n P _ n ( - 1 ) = ( - 1 ) ^ n P n ( − 1 ) = ( − 1 ) n
تعامد چندجملهایهای لژاندر
چندجملهایای لژاندر P m ( x ) P _ m ( x ) P m ( x ) P n ( x ) P _ n ( x ) P n ( x ) − 1 ≤ x ≤ 1 - 1 \le x \le 1 − 1 ≤ x ≤ 1
∫ − 1 1 P m ( x ) P n ( x ) d x = 0 m ≠ n \large \int _ { - 1 } ^ { 1 } \mathrm { P } _ { m} ( x ) \mathrm { P } _ { n } ( x ) d x = 0 \quad \quad m \neq n ∫ − 1 1 P m ( x ) P n ( x ) d x = 0 m = n
و در نتیجه، داریم:
∫ − 1 1 [ P n ( x ) ] 2 d x = 2 2 n + 1 m = n \large \int _ { - 1 } ^ { 1 } \left [ \mathrm { P } _ { n } ( x ) \right ] ^ { 2 } d x = \frac { 2 } { 2 n + 1 } \quad m = n ∫ − 1 1 [ P n ( x ) ] 2 d x = 2 n + 1 2 m = n
سری متعامد چندجملهایهای لژاندر
هر تابع f ( x ) f ( x ) f ( x ) − 1 ≤ x ≤ 1 -1 \le x \le 1 − 1 ≤ x ≤ 1 ناپیوستگی در این بازه داشته باشد، میتوان با یک سری از چندجملهایهای لژاندر بیان کرد.
تابع را به صورت زیر مینویسیم:
f ( x ) = A 0 P 0 ( x ) + A 1 P 1 ( x ) + A 2 P 2 ( x ) + … − 1 ≤ x ≤ 1 = ∑ n = 0 ∞ A n P n ( x ) \large \begin {aligned} f ( x ) & = A _ { 0 } \mathrm { P } _ { 0 } ( x ) + A _ { 1 } \mathrm { P } _ { 1 } ( x ) + A _ { 2 } \mathrm { P } _ { 2 }( x ) + \ldots \quad - 1 \leq x \leq 1 \\ & = \sum _ { n = 0 } ^ { \infty } A _ { n } \mathrm { P } _ { n } ( x ) \end {aligned} f ( x ) = A 0 P 0 ( x ) + A 1 P 1 ( x ) + A 2 P 2 ( x ) + … − 1 ≤ x ≤ 1 = n = 0 ∑ ∞ A n P n ( x )
با ضرب هر دو طرف رابطه در P m ( x ) d x P _ m ( x ) d x P m ( x ) d x انتگرالگیری نسبت به x x x x = − 1 x = - 1 x = − 1 x = 1 x = 1 x = 1
∫ − 1 1 f ( x ) P m ( x ) d x = ∑ n = 0 ∞ A n ∫ − 1 1 P m ( x ) P n ( x ) d x \large \int _ { - 1 } ^ {1 } f ( x ) P _ { m } ( x ) d x = \sum _ { n =0 } ^ { \infty } A _ { n } \int _ { - 1 } ^ { 1 } P _ { m } ( x ) P _ { n } ( x ) d x ∫ − 1 1 f ( x ) P m ( x ) d x = n = 0 ∑ ∞ A n ∫ − 1 1 P m ( x ) P n ( x ) d x
با توجه به ویژگی تعامد چندجملهایهای لژاندر میتوان نوشت:
A n = 2 n + 1 2 ∫ − 1 1 f ( x ) P n ( x ) d x n = 0 , 1 , 2 , 3 … \large A _ { n } = \frac { 2 n + 1 } { 2 } \int _ { - 1 } ^ { 1 } f ( x ) P _ { n } ( x ) d x \quad n = 0 , 1 , 2 , 3 \dots A n = 2 2 n + 1 ∫ − 1 1 f ( x ) P n ( x ) d x n = 0 , 1 , 2 , 3 …
از آنجا که با زوج بودن n n n P n ( x ) P _ n ( x ) P n ( x ) تابع زوج از x x x n n n P n ( x ) P _ n ( x ) P n ( x ) n n n f ( x ) f ( x ) f ( x ) A n A_ n A n
در نتیجه، برای تابع زوج f ( x ) f ( x ) f ( x )
A n = { 0 n is odd ( 2 n + 1 ) ∫ 0 1 f ( x ) P n ( x ) d x n is even \large A _ { n } = \left \{ \begin {array} {ll} { 0 } & { n \text { is odd }} \\ { ( 2 n + 1 ) \int _ { 0 } ^ { 1 } f ( x ) P _ { n } ( x ) d x } & { n \text { is even }} \end {array} \right . A n = { 0 ( 2 n + 1 ) ∫ 0 1 f ( x ) P n ( x ) d x n is odd n is even
در حالی که برای تابع فرد f ( x ) f ( x ) f ( x )
A n = { ( 2 n + 1 ) ∫ 0 1 f ( x ) P n ( x ) d x n is odd 0 n is even \large A _ { n } = \left \{ \begin {array} {ll} { ( 2 n + 1 ) \int _ { 0 } ^ { 1 } f ( x ) P _ { n } ( x ) d x } & { n \text { is odd }} \\ { 0} & { n \text { is even }} \end {array} \right . A n = { ( 2 n + 1 ) ∫ 0 1 f ( x ) P n ( x ) d x 0 n is odd n is even
وقتی x = cos θ x = \cos \theta x = cos θ f ( θ ) f ( \theta) f ( θ )
f ( θ ) = ∑ n = 0 ∞ A n P n ( cos θ ) 0 ≤ θ ≤ π \large f ( \theta ) = \sum _ { n = 0 } ^ { \infty } A _ { n } \mathrm { P } _ { n } ( \cos \theta ) \quad 0 \leq \theta \leq \pi f ( θ ) = n = 0 ∑ ∞ A n P n ( cos θ ) 0 ≤ θ ≤ π
که در آن:
A n = 2 n + 1 2 ∫ 0 π f ( θ ) P n ( cos θ ) sin θ d θ n = 0 , 1 , 2 , 3 … \large A _ { n } = \frac { 2 n + 1 } { 2 } \int _ { 0 } ^ { \pi } f ( \theta ) P _ { n } ( \cos \theta ) \sin \theta d \theta \quad n = 0 , 1 , 2 , 3 \dots A n = 2 2 n + 1 ∫ 0 π f ( θ ) P n ( cos θ ) sin θ d θ n = 0 , 1 , 2 , 3 …
ویژگیهای چندجملهایهای لژاندر
فرم انتگرالی چندجملهای لژاندر به صورت زیر است:
P n ( x ) = 1 π ∫ 0 π [ x + x 2 − 1 cos t ] n d t \large \mathrm { P } _ { n } ( x ) = \frac { 1 } { \pi } \int _ { 0 } ^ { \pi } [ x + \sqrt { x ^ { 2 } - 1 } \cos t ] ^ { n } d t P n ( x ) = π 1 ∫ 0 π [ x + x 2 − 1 cos t ] n d t
مقادیر P n ( x ) P _ n ( x ) P n ( x ) x = 0 x = 0 x = 0 x = ± 1 x = \pm 1 x = ± 1
P 2 n ( 0 ) = ( − 1 ) n Γ ( n + 1 / 2 ) π Γ ( n + 1 ) P 2 n + 1 ( 0 ) = 0 P 2 n ′ ( 0 ) = 0 P 2 n + 1 ′ ( 0 ) = ( − 1 ) n 2 Γ ( n + 3 / 2 ) π Γ ( n + 1 ) P n ( 1 ) = 1 P n ( − 1 ) = ( − 1 ) n P n ′ ( 1 ) = n ( n + 11 ) 2 P n ′ ( − 1 ) = ( − 1 ) n − 1 n ( n + 1 ) 2 ∣ P n ( x ) ∣ ≤ 1 \large \begin {aligned} & \begin {array} { l l } { \mathrm { P } _ { 2 \mathrm { n } } ( 0 ) = \frac { ( - 1 ) ^ { n } \Gamma ( n + 1 / 2 ) } { \sqrt { \pi \Gamma }( n + 1 ) } } & { \mathrm { P } _ { 2 n + 1 } ( 0 )= 0 } \\ { \mathrm { P } _ { 2 n } ^ { \prime } ( 0 ) = 0 } & { \mathrm { P } _ { 2 n + 1 } ^ { \prime } ( 0 ) = \frac { ( - 1 ) ^ { n } 2 \Gamma ( n + 3 / 2 ) } { \sqrt { \pi \Gamma ( n+1 ) } } } \end {array} \\ & \mathrm { P } _ { n } ( 1 ) = 1 \quad \quad \quad\quad\quad\quad\quad \mathrm { P } _ {n } ( - 1 ) = ( - 1) ^ { n } \\ &\mathrm { P } _ { n } ^ { \prime } ( 1 ) = \frac { n ( n + 1 1 )} { 2 } \quad \quad P_ {n } ^ { \prime } ( - 1 ) = (- 1 ) ^ { n - 1 }\frac { n ( n + 1 ) } { 2 } \\ & \left | \mathrm { P } _ { n } ( x ) \right | \leq 1 \end {aligned} P 2 n ( 0 ) = π Γ ( n + 1 ) ( − 1 ) n Γ ( n + 1/2 ) P 2 n ′ ( 0 ) = 0 P 2 n + 1 ( 0 ) = 0 P 2 n + 1 ′ ( 0 ) = π Γ ( n + 1 ) ( − 1 ) n 2Γ ( n + 3/2 ) P n ( 1 ) = 1 P n ( − 1 ) = ( − 1 ) n P n ′ ( 1 ) = 2 n ( n + 11 ) P n ′ ( − 1 ) = ( − 1 ) n − 1 2 n ( n + 1 ) P n ( x ) ≤ 1
علامتهای پریم مشتق نسبت به x x x x = 1 x = 1 x = 1 P n ′ ( 1 ) = d P n ( x ) ) d x \mathrm { P }' _ n ( 1 ) = \frac { d \mathrm { P } _ n ( x ) )} { d x } P n ′ ( 1 ) = d x d P n ( x ))
تابع مولد چندجملهایهای لژاندر
اگر A A A ( x 1 , y 1 , z 1 ) ( x _ 1 , y _ 1 , z _ 1 ) ( x 1 , y 1 , z 1 ) P P P ( x , y , z ) ( x , y , z ) ( x , y , z ) A P AP A P R R R
R 2 = ( x − x 1 ) 2 + ( y − y 1 ) 2 + ( z − z 0 ) 2 \large R ^ 2 = ( x - x _ 1 ) ^ 2 + ( y - y _ 1 ) ^ 2 + ( z - z _ 0 ) ^ 2 R 2 = ( x − x 1 ) 2 + ( y − y 1 ) 2 + ( z − z 0 ) 2
با توجه به قضیه پتانسیل نیوتنی میدانیم که پتانسیل در نقطه P P P A A A
ϕ = C R \large \phi = \frac { C } { R } ϕ = R C
که C C C
در برخی شرایط، میخواهیم ϕ \phi ϕ r r r r − 1 r ^ { - 1 } r − 1 r = x 2 + y 2 + z 2 r = \sqrt { x ^ 2 + y ^ 2 + z ^ 2 } r = x 2 + y 2 + z 2 O O O P P P
شکل ۳: تابع مولد چندجملهای لژاندر در شکل بالا:
a = ∣ O A → ∣ , r = ∣ O B → ∣ , ϕ = C R = c r 2 + a 2 − 2 cos − 1 θ \large a = | \overrightarrow {OA} | , \; r = | \overrightarrow {OB}| , \; \phi = \frac { C } { R} = \frac { c } { \sqrt { r ^ 2 + a ^ 2 - 2 \cos ^ { - 1 } \theta }} a = ∣ O A ∣ , r = ∣ OB ∣ , ϕ = R C = r 2 + a 2 − 2 cos − 1 θ c
با جایگذاری، میتوان نوشت:
ϕ = C r [ 1 − 2 x t + t 2 ] − 1 / 2 \large \phi = \frac { C } { r } [ 1 - 2 x t + t ^ 2 ] ^ { - 1 / 2 } ϕ = r C [ 1 − 2 x t + t 2 ] − 1/2
که در آن:
t = a r , x = cos θ \large t = \frac { a } { r } , \;\;\;\;\; x = \cos \theta t = r a , x = cos θ
بنابراین:
ϕ ≡ C r g ( x , t ) \large \phi \equiv \frac { C } { r } g ( x , t ) ϕ ≡ r C g ( x , t )
زاویه θ \theta θ O A → \overrightarrow { O A } O A O P → \overrightarrow { O P } OP
R 2 = r 2 + a 2 − 2 cos − 1 θ \large R ^ 2 = r ^ 2 + a ^ 2 - 2 \cos ^ { - 1 } \theta R 2 = r 2 + a 2 − 2 cos − 1 θ
که در آن، a = ∣ O A → ∣ a= | \overrightarrow { O A } | a = ∣ O A ∣ r / R = t r / R = t r / R = t x = cos θ x = \cos \theta x = cos θ
g ( x , t ) = ( 1 − 2 x t + t 2 ) − 1 / 2 \large g ( x , t ) = ( 1 - 2 x t + t ^ 2 ) ^ { - 1 / 2 } g ( x , t ) = ( 1 − 2 x t + t 2 ) − 1/2
که به عنوان تابع مولد برای P n ( x ) \mathrm { P } _ n ( x ) P n ( x ) بسط دوجملهای ، داریم:
g ( x , t ) = ∑ n = 0 ∞ ( 1 2 ) n ( 2 x t − t 2 ) n n ! \large g ( x , t ) = \sum _ { n = 0 } ^ { \infty } \left ( \frac { 1 } { 2 } \right ) n \frac { \left ( 2 x t - t ^ { 2 } \right ) ^ { n } } { n ! } g ( x , t ) = n = 0 ∑ ∞ ( 2 1 ) n n ! ( 2 x t − t 2 ) n
نماد ( α ) n ( \alpha ) _ n ( α ) n
( α ) n = α ( α + 1 ) ( α + 2 ) … ( α + n − 1 ) = Π k = 0 n − 1 ( α + k ) ( α ) 0 = 1 \large \begin {array} { l } { ( \alpha ) _ { n } = \alpha ( \alpha + 1 ) ( \alpha + 2 ) \ldots ( \alpha + n - 1 ) = \Pi_ { k = 0 } ^ { n - 1 } ( \alpha + k ) } \\ { ( \alpha ) _ { 0 } = 1 } \end {array} ( α ) n = α ( α + 1 ) ( α + 2 ) … ( α + n − 1 ) = Π k = 0 n − 1 ( α + k ) ( α ) 0 = 1
بنابراین، داریم:
g ( x , t ) = ∑ n = 0 ∞ ( 1 / 2 ) n n ! ∑ k = 0 n n ! ( 2 x ) n − k t n − k ( − t 2 ) k k ! ( n − k ) ! \large g ( x , t ) = \sum _ { n = 0 } ^ { \infty } \frac { (1 / 2 ) n } { n ! } \sum _ { k = 0 } ^ { n } \frac { n ! ( 2 x ) ^ { n - k } t ^ { n - k } \left ( - t ^ { 2 } \right ) ^ { k } } { k ! ( n - k ) ! } g ( x , t ) = n = 0 ∑ ∞ n ! ( 1/2 ) n k = 0 ∑ n k ! ( n − k )! n ! ( 2 x ) n − k t n − k ( − t 2 ) k
که میتوان نوشت:
g ( x , t ) = ( 1 − 2 x t + t 2 ) − 1 / 2 = ∑ n = 0 ∞ [ ∑ k = 0 n / 2 ( − 1 ) k ( 2 n − 2 k ) ! x n − 2 k 2 k ! ( n − k ) ! ] t n \large g ( x , t ) = \left ( 1 - 2 x t + t ^ { 2 } \right ) ^ { - 1 / 2 } = \sum _ { n = 0 } ^ { \infty } \left [ \sum _ { k = 0 } ^ { n / 2 } \frac { ( - 1 ) ^ { k } ( 2 n - 2 k ) ! x ^ { n - 2 k } } { 2 k ! ( n - k ) ! } \right ] t ^ { n } g ( x , t ) = ( 1 − 2 x t + t 2 ) − 1/2 = n = 0 ∑ ∞ k = 0 ∑ n /2 2 k ! ( n − k )! ( − 1 ) k ( 2 n − 2 k )! x n − 2 k t n
ضریب t n t ^ n t n P n ( x ) \mathrm { P} _ n ( x ) P n ( x ) t n t ^ n t n
g ( x , t ) = ( 1 − 2 x t + t 2 ) − 1 / 2 = ∑ n = 0 ∞ P n ( x ) t n ∣ x ∣ ≤ 1 , ∣ t ∣ < 1 \large \begin {aligned} & g ( x , t ) = \left ( 1 - 2 x t + t ^ { 2 } \right ) ^ { - 1 / 2 } = \sum _ { n = 0 } ^ { \infty } P _ { n } ( x ) t ^ { n } \ \ & | x | \leq 1 , | t | < 1 \end {aligned} g ( x , t ) = ( 1 − 2 x t + t 2 ) − 1/2 = n = 0 ∑ ∞ P n ( x ) t n ∣ x ∣ ≤ 1 , ∣ t ∣ < 1
توابع لژاندر نوع دوم
جوابهای دوم و خطی مستقل معادله لژاندر برای n n n
Q n ( x ) = 1 2 P n ( x ) ln 1 + x 1 − x = W n − 1 ( x ) \large \mathrm { Q } _ { n } ( x ) = \frac { 1 } { 2 } \mathrm { P } _ { n } ( x ) \ln \frac { 1 + x } { 1 -x } = \mathrm { W } _ { n - 1 } ( x ) Q n ( x ) = 2 1 P n ( x ) ln 1 − x 1 + x = W n − 1 ( x )
که
W n − 1 ( x ) = ∑ m = 1 n 1 m P m − 1 ( x ) P n − m ( x ) \large \mathrm { W } _ { n - 1 } ( x ) = \sum _ { m = 1 } ^ { n } \frac { 1 } { m } \mathbf { P } _ { m - 1 } ( x ) \mathrm { P } _ { n - m } ( x ) W n − 1 ( x ) = m = 1 ∑ n m 1 P m − 1 ( x ) P n − m ( x )
یک چندجملهای درجه ( n − 1 ) ( n - 1 ) ( n − 1 ) Q n ( x ) \mathrm { Q} _ n ( x ) Q n ( x ) x = ± 1 x = \pm 1 x = ± 1 θ = 0 \theta = 0 θ = 0 π \pi π
چند چندجملهای نخست به صورت زیر هستند:
Q 0 ( x ) = 1 2 ln 1 + x 1 − x Q 1 ( x ) = P 1 ( x ) Q 0 ( x ) − 1 Q 2 ( x ) = P 2 ( x ) Q 0 ( x ) − 3 2 x Q 3 ( x ) = P 3 ( x ) Q 0 ( x ) − 5 2 x 2 + 2 3 \large \begin {aligned} & \mathrm { Q } _ { 0 } ( x ) = \frac { 1 } { 2 } \ln \frac { 1 + x } { 1 - x } \\ & \mathrm { Q } _ { 1 } ( { x } ) = \mathrm { P } _ { 1 } ( { x } ) \mathrm { Q } _ { 0 } ( { x } ) - 1 \\ & \mathrm { Q } _ { 2 } ( x ) = \mathrm { P } _ { 2 } ( x ) \mathrm { Q } _ { 0 } ( x ) - \frac { 3 } { 2 } x\\ & \mathrm { Q } _ { 3 } ( x ) = \mathrm { P } _ { 3 } ( x ) \mathrm { Q } _ { 0 } ( x ) - \frac { 5 } { 2 } x ^ { 2 } + \frac { 2 } { 3 } \end {aligned} Q 0 ( x ) = 2 1 ln 1 − x 1 + x Q 1 ( x ) = P 1 ( x ) Q 0 ( x ) − 1 Q 2 ( x ) = P 2 ( x ) Q 0 ( x ) − 2 3 x Q 3 ( x ) = P 3 ( x ) Q 0 ( x ) − 2 5 x 2 + 3 2
این چندجملهایها توابع درجه زوجی را نشان میدهند که باید در x x x
چندجملهای مرتبه بالاتر Q n ( x ) \mathrm { Q } _ n ( x ) Q n ( x ) P n ( x ) \mathrm { P } _ n ( x ) P n ( x )
روابط بیشماری با استفاده از توابع لژاندر میتوان در قالب نظریه آنالیز مختلط به دست آورد. یکی از این رابطهها رابطه انتگرالی Q n ( x ) \mathrm { Q} _ n ( x ) Q n ( x )
Q n ( x ) = ∫ 0 ∞ [ x + x 2 − 1 cosh θ ] − n − 1 d θ ∣ x ∣ > 1 \large \mathrm { Q } _ { n } ( x ) = \int _ { 0 } ^ { \infty } [ x + \sqrt { x ^ { 2 } - 1 } \cosh \theta ] ^ { -n - 1 } d \theta \quad | x | > 1 Q n ( x ) = ∫ 0 ∞ [ x + x 2 − 1 cosh θ ] − n − 1 d θ ∣ x ∣ > 1
و تابع مولد آن به صورت زیر است:
( 1 − 2 x t + t 2 ) − 1 / 2 cosh − 1 t − x x 2 − 1 = ∑ n = 0 ∞ Q n ( x ) t n \large \left ( 1 - 2 x t + t ^ { 2 } \right ) ^ { - 1 / 2 } \cosh ^ { - 1 } \frac { t - x } { \sqrt { x ^ { 2 } - 1 } } = \sum _ { n = 0 } ^ { \infty } \mathrm { Q } _ { n } ( x ) t ^ { n } ( 1 − 2 x t + t 2 ) − 1/2 cosh − 1 x 2 − 1 t − x = n = 0 ∑ ∞ Q n ( x ) t n
برخی از مقادیر خاص Q n ( x ) \mathrm {Q}_ n ( x ) Q n ( x )
Q 2 n ( 0 ) = 0 Q 2 n + 1 ( 0 ) = ( − 1 ) n + 1 2 ⋅ 4 ⋅ 6 ⋅ ⋯ 2 n 1 ⋅ 3 ⋅ 5 ⋅ ⋯ ( 2 n − 1 ) Q n ( 1 ) = ∞ Q n ( − x ) = ( − 1 ) n + 1 Q n ( x ) \large \begin {aligned} \mathrm { Q } _ { 2 n } ( 0 ) & = 0 & & \mathrm { Q } _ { 2 n + 1 } ( 0 ) = ( - 1 ) ^ { n + 1 } \frac { 2 \cdot 4 \cdot 6 \cdot \cdots 2 n } { 1 \cdot 3 \cdot 5 \cdot \cdots ( 2 n - 1 ) } \\ \mathrm { Q } _ { n } ( 1 ) & = \infty & & \mathrm { Q } _ { n } ( - x ) = ( - 1 ) ^ { n + 1 } \mathrm { Q } _ { n } ( x ) \end {aligned} Q 2 n ( 0 ) Q n ( 1 ) = 0 = ∞ Q 2 n + 1 ( 0 ) = ( − 1 ) n + 1 1 ⋅ 3 ⋅ 5 ⋅ ⋯ ( 2 n − 1 ) 2 ⋅ 4 ⋅ 6 ⋅ ⋯ 2 n Q n ( − x ) = ( − 1 ) n + 1 Q n ( x )
معادله دیفرانسیل وابسته لژاندر
معادله دیفرانسیلِ
( 1 − x 2 ) d 2 y d x 2 − 2 x d y d x + [ n ( n + 1 ) − m 2 1 − x 2 ] y = 0 \large \left ( 1 - x ^ { 2 } \right ) \frac { d ^ { 2 } y } { d x ^ { 2} } - 2 x \frac { d y } { d x } + \left [ n ( n + 1 ) - \frac { m ^ { 2 } } { 1 -x ^ { 2 } } \right ] y = 0 ( 1 − x 2 ) d x 2 d 2 y − 2 x d x d y + [ n ( n + 1 ) − 1 − x 2 m 2 ] y = 0
معادله دیفرانسیل وابسته لژاندر نامیده میشود. اگر m = 0 m = 0 m = 0 m m m n n n
y = A P n m ( x ) + B Q n m ( x ) \large y = A \mathrm { P } _ n ^ m ( x ) + B \mathrm { Q } _ n ^ m ( x ) y = A P n m ( x ) + B Q n m ( x )
که در آن، P n m \mathrm { P } _ n ^ m P n m Q n m ( x ) \mathrm { Q } _ n ^ m ( x ) Q n m ( x )
P n m ( x ) = ( 1 − x 2 ) m / 2 d m d x m P n ( x ) Q n m ( x ) = ( 1 − x 2 ) m / 2 d m d x m Q n ( x ) \large \begin {array} { l } { \mathrm { P } _ { n } ^ { m } ( x ) = \left ( 1 -x ^ { 2 } \right ) ^ { m / 2 } \frac { d ^ { m } } { d x ^ { m } } \mathrm { P } _ { n } ( x ) } \\ { \mathrm { Q } _ { n } ^ { m } ( x ) = \left ( 1 - x ^ { 2 } \right ) ^ { m / 2 } \frac { d ^ { m } } { d x ^ { m } } \mathrm { Q } _ { n } ( x ) } \end {array} P n m ( x ) = ( 1 − x 2 ) m /2 d x m d m P n ( x ) Q n m ( x ) = ( 1 − x 2 ) m /2 d x m d m Q n ( x )
توابع P n m ( x ) \mathrm { P} _ n ^ m ( x ) P n m ( x ) − 1 ≤ x ≤ 1 - 1 \le x \le 1 − 1 ≤ x ≤ 1 Q n m ( x ) \mathrm { Q } _ n ^ m ( x ) Q n m ( x ) x ± 1 x \pm 1 x ± 1
چند تابع وابسته لژاندر نوع اول به شرح زیر هستند:
P n 0 ( x ) = P n ( x ) P n m ( x ) = ( 1 − x 2 ) m / 2 2 n n ! d m + n d x m + n ( x 2 − 1 ) n = 0 m > n P 1 ′ ( x ) = ( 1 − x 2 ) 1 / 2 P 3 ′ ( x ) = 3 2 ( 5 x 2 − 1 ) ( 1 − x 2 ) 1 / 2 P 2 ′ ( x ) = 3 x ( 1 − x 2 ) 1 / 2 P 3 2 ( x ) = 15 x ( 1 − x 2 ) P 2 2 ( x ) = 3 ( 1 − x 2 ) P 3 3 ( x ) = 15 ( 1 − x 2 ) 3 / 2 \large \begin {array} { l l } { \mathrm { P } _ { n } ^ { 0 } (x ) = } { \mathrm { P } _ { n } ( x ) } \\ { \mathrm { P } _ { n } ^ { m } ( x ) = \frac { \left ( 1 -x ^ { 2 } \right ) ^ { m / 2 } } { 2 ^ { n } n ! } \frac { d ^ { m + n } } {d x ^ { m+ n } } \left ( x ^ { 2 } - 1 \right ) ^ { n } = 0 } & { m > n } \\ { \mathrm { P } _ { 1 } ^ { \prime } ( x ) = \left ( 1 - x ^ { 2 } \right ) ^ { 1 / 2 } } & { \mathrm { P } _ { 3 } ^ { \prime } ( x ) = \frac { 3 } { 2 } \left ( 5 x ^ { 2 } - 1 \right ) \left ( 1 - x ^ { 2 } \right ) ^ { 1 / 2 } } \\ { \mathrm { P } _ { 2 } ^ { \prime } ( x ) = 3 x \left ( 1 -x ^ { 2 } \right ) ^ { 1 / 2 } } & { \mathrm { P } _ { 3 } ^ { 2 } ( x ) = 1 5 x \left ( 1 - x ^ { 2 } \right ) } \\ { \mathrm { P } _ { 2 } ^ { 2 } ( x ) = 3 \left ( 1 -x ^ { 2 } \right ) } & { \mathrm { P } _ { 3 } ^ { 3 } ( x ) = 1 5 \left ( 1 - x ^ { 2 } \right ) ^ { 3 / 2 } } \end {array} P n 0 ( x ) = P n ( x ) P n m ( x ) = 2 n n ! ( 1 − x 2 ) m /2 d x m + n d m + n ( x 2 − 1 ) n = 0 P 1 ′ ( x ) = ( 1 − x 2 ) 1/2 P 2 ′ ( x ) = 3 x ( 1 − x 2 ) 1/2 P 2 2 ( x ) = 3 ( 1 − x 2 ) m > n P 3 ′ ( x ) = 2 3 ( 5 x 2 − 1 ) ( 1 − x 2 ) 1/2 P 3 2 ( x ) = 15 x ( 1 − x 2 ) P 3 3 ( x ) = 15 ( 1 − x 2 ) 3/2
فرمولهای بازگشتی P n m ( x ) \mathrm { P } _n ^ m ( x ) P n m ( x )
( n + 1 − m ) P n + 1 m ( x ) = ( 2 n + 1 ) x P n m ( x ) − ( n + m ) P n − 1 m ( x ) P n m + 2 ( x ) = 2 ( m + 1 ) ( 1 − x 2 ) 1 / 2 x P n m + 1 − ( n − m ) ( n + m + 1 ) P n m ( x ) \large \begin {aligned} ( n + 1 - m ) \mathrm { P } _ { n + 1 } ^ { m } ( x ) & =( 2 n + 1 ) x P _ { n } ^ { m } ( x ) - ( n + m ) \mathrm { P } _ { n - 1 } ^ { m } ( x ) \\ P _ { n } ^ { m + 2 } ( x ) & = \frac { 2 ( m + 1 ) } { \left ( 1 - x ^ { 2 } \right ) ^ { 1 / 2 } } x P _ { n } ^ { m + 1 } - ( n - m ) ( n + m + 1 ) P _ { n } ^ { m } ( x ) \end {aligned} ( n + 1 − m ) P n + 1 m ( x ) P n m + 2 ( x ) = ( 2 n + 1 ) x P n m ( x ) − ( n + m ) P n − 1 m ( x ) = ( 1 − x 2 ) 1/2 2 ( m + 1 ) x P n m + 1 − ( n − m ) ( n + m + 1 ) P n m ( x )
تعامد P n m ( x ) \Large \mathrm { P } _ n ^ m ( x ) P n m ( x )
مشابه چندجملهای لژاندر، توابع لژاندر P n ( x ) \mathrm {P}_ n ( x ) P n ( x ) − 1 ≤ x ≤ 1 -1 \le x \le 1 − 1 ≤ x ≤ 1
∫ − 1 1 P n m ( x ) P k m ( x ) d x = 0 n ≠ k \large \int _ { - 1 } ^ { 1 } \mathrm { P } _ { n } ^ { m } ( x ) \mathrm { P } _ { k } ^ { m } ( x ) d x = 0 \quad n \neq k ∫ − 1 1 P n m ( x ) P k m ( x ) d x = 0 n = k
و همچنین:
∫ − 1 1 [ P n m ( x ) ] 2 d x = 2 2 n + 1 ( n + m ) ! ( n − m ) ! \large \int _ { - 1 } ^ { 1 } \left [ \mathrm { P } _ { n } ^ { m } ( x ) \right ] ^ { 2 } d x = \frac { 2 } { 2 n + 1 } \frac { ( n + m ) ! } { ( n - m ) ! } ∫ − 1 1 [ P n m ( x ) ] 2 d x = 2 n + 1 2 ( n − m )! ( n + m )!
سری تعامد توابع لژاندر وابسته
هر تابع f ( x ) f ( x ) f ( x ) − 1 ≤ x ≤ 1 - 1 \le x \le 1 − 1 ≤ x ≤ 1
f ( x ) = A m P 1 m ( x ) + A m + 1 P m + 1 m ( x ) + A m + 2 P m + 2 m ( x ) + ⋯ \large f ( x ) = A _{ m } P _ { 1 } ^ { m } ( x ) + A _ { m + 1 } P _ { m + 1 } ^ { m } ( x ) + A _ { m + 2 } P _ { m+ 2 } ^ { m } ( x ) + \cdots f ( x ) = A m P 1 m ( x ) + A m + 1 P m + 1 m ( x ) + A m + 2 P m + 2 m ( x ) + ⋯
که در آن، ضرایب به صورت زیر تعیین میشوند:
A k = 2 k + 1 2 ( k − m ) ! ( k + m ) ! ∫ − 1 1 f ( x ) P k m ( x ) d x \large A _ { k } = \frac { 2 k + 1 } { 2 } \frac { ( k - m) ! } { ( k + m ) ! } \int _ { - 1 } ^ { 1 } f ( x ) P _ { k } ^ { m } ( x ) d x A k = 2 2 k + 1 ( k + m )! ( k − m )! ∫ − 1 1 f ( x ) P k m ( x ) d x
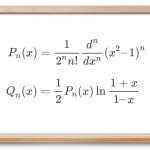
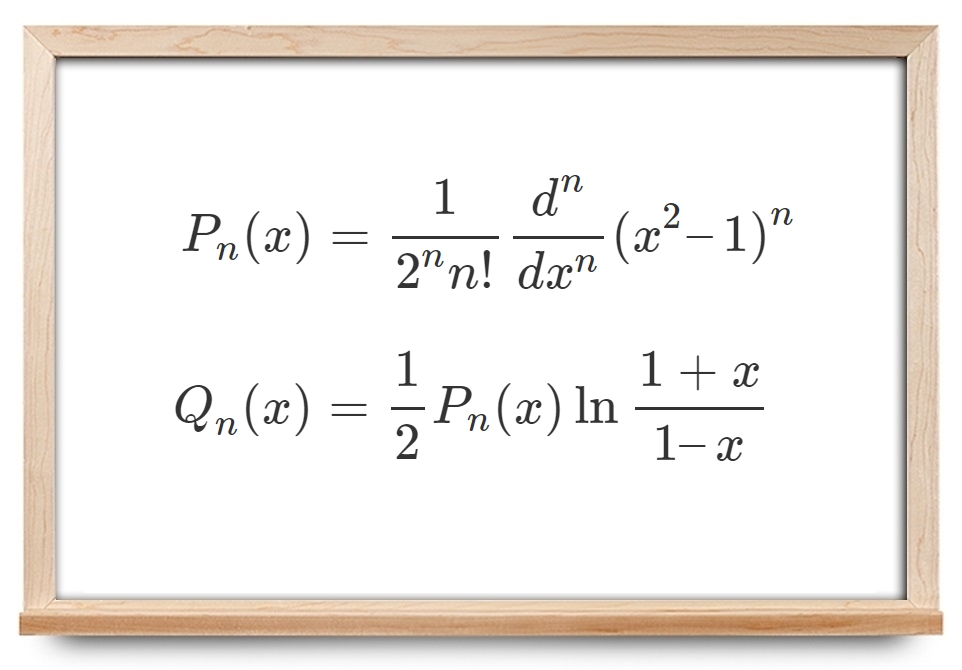
 )" width="419" height="244">
)" width="419" height="244">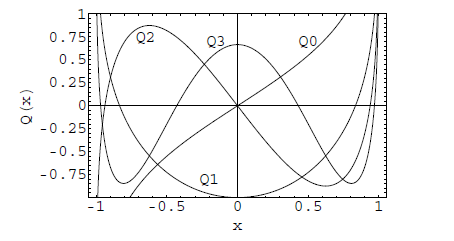 )" width="454" height="241">
)" width="454" height="241">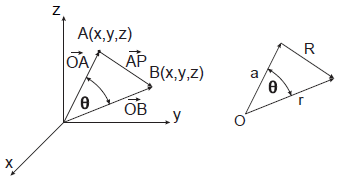











دستتون درد نکنه عالی بود
سلام وقتتون بخیر ممنون بابت توضیحات جامع و مفیدتون
ببخشید بنده یک سوال داشتم چطور ممکنه معادله ی لژاندر در نقطه x= بی نهایت تکینگی منظم داشته باشه؟