تابع تحلیلی — به زبان ساده
در آموزشهای پیشن از مجموعه آموزشهای ریاضیات مجله فرادرس، با توابع مختلط و حد و مشتق آنها آشنا شدیم. در این آموزش، مفاهیم مربوط به «تابع تحلیلی» (Analytic Function) را ارائه کرده و با نقاط تکین توابع مختلط آشنا میشویم.
تعاریف و قضایای تابع تحلیلی
در این بخش، چند تعریف و قضیه مربوط به تابع تحلیل را بیان میکنیم.
تعریف ۱: تابع $$ f ( z ) $$ را در ناحیه $$ \mathcal { R} $$ از صفحه مختلط تحلیلی میگوییم، اگر $$ f ( z ) $$ در هر نقطه از $$ \mathcal { R} $$ دارای مشتق بوده و همچنین، تکمقداره باشد.
تعریف ۲: تابع $$ f ( z ) $$ را در نقطه $$ z $$ تحلیلی میگوییم، اگر $$ z $$ یک نقطه درون ناحیهای باشد که $$ f ( z ) $$ در آن تحلیلی است.
بنابراین، مفهوم تابع تحلیلی در یک نقطه بیان میکند که آن تابع در دایرهای به مرکز آن نقطه تحلیلی است.
نتیجه: اگر $$ f ( z ) $$ در نقطه $$ z $$ تحلیلی باشد، آنگاه $$ f ( z ) $$ دارای همه مشتقات (همه مراتب) در نقطه $$ z $$ است.
تابع مختلطی که بر تمام صفحه مختلط، تحلیلی باشد، «تابع تام» (Entire Function) نام داد.
شرایط تحلیلی بودن تابع مختلط
در ادامه، شرایط لازم و کافی تحلیلی بودن تابع را معرفی میکنیم.
شرط لازم تحلیلی بودن
تابع مختلط زیر را در نظر بگیرید:
$$ \large f ( x , y ) = u ( x , y ) + i v ( x , y ) $$
از آنجا که $$ x = ( z + z ^ * ) / 2 $$ و $$ y = ( z - z ^ * ) / 2 $$، با جایگذاری $$ x $$ و $$ y $$، خواهیم داشت ($$ z ^ * $$ مزدوج مختلط $$ z $$ است):
$$ \large f ( z , z ^ * ) = u ( x , y ) + i v ( x , y ) $$
یک شرط لازم برای تحلیلی بودن $$ f ( z , z ^ * ) $$ به صورت زیر است:
$$ \frac { \partial f } { \partial z ^ * } = 0 . \;\;\;\;\; ( 1 ) $$
بنابراین، یک شرط لازم برای تحلیلی بودن $$ f = u + i v $$ این است که $$ f $$ فقط به $$ z $$ وابسته باشد. شرط (۱) را میتوان برحسب بخشهای حقیقی و موهومی $$ u $$ و $$ v $$ تابع $$ f $$ به شکل معادل زیر بیان کرد:
$$ \large \begin {align*} \frac { \partial u} { \partial x } & = \frac { \partial v} { \partial y } \;\;\;\;\; \;\;\; ( 2 ) \\ \frac { \partial u} { \partial y } & = - \frac { \partial v} { \partial x } \;\;\;\;\; ( 3 ) \end {align*} $$
معادلات (۲) و (۳) به عنوان معادلات کوشی-ریمان شناخته میشوند. این معادلات شرایط لازم برای تحلیلی بودن $$ f = u + i v $$ هستند.
شرایط لازم و کافی تحلیلی بودن تابع
شرایط لازم و کافی برای آنکه تابع $$ f = u + i v $$ تحلیلی باشد، به شرح زیر است:
- چهار مشتق $$ \frac { \partial u } { \partial x } $$، $$ \frac { \partial v } { \partial y } $$، $$ \frac { \partial u } { \partial y } $$ و $$ \frac { \partial v } { \partial x } $$ مربوط بخشهای حقیقی و موهومی در معادلات کوشی-ریمان (۲) و (۳) صدق کنند.
- چهار مشتق $$ \frac { \partial u } { \partial x } $$، $$ \frac { \partial v } { \partial y } $$، $$ \frac { \partial u } { \partial y } $$ و $$ \frac { \partial v } { \partial x } $$ مربوط بخشهای حقیقی و موهومی، پیوسته باشند.
قضیه
اگر $$ f ( z ) $$ تحلیلی باشد، آنگاه داریم:
$$ \large \begin {align*}
& \frac { \partial ^ { 2 } u } { \partial x ^ { 2 } } + \frac { \partial ^ { 2 } u } { \partial y ^ { 2 } } = 0 \;\;\;\;\; ( 4 ) \\
& \frac { \partial ^ { 2 } v } { \partial x ^ { 2 } } + \frac { \partial ^ { 2 } v } { \partial y ^ { 2 } } = 0 \;\;\;\;\; ( 5 )
\end {align*} $$
بخشهای حقیقی و موهومی یک تابع تحلیلی، توابع مزدوج هارمونیک هستند، یعنی جوابهای معادله لاپلاس بوده و در معادلات کوشی-ریمان (۲) و (۳) صدق میکنند.
تکینگی توابع تحلیلی
نقاطی که در آنها تابع $$ f ( z ) $$ تحلیلی نیست، نقاط تکین یا تکینگیهای $$ f ( z ) $$ نامیده میشوند. دو نوع مختلف نقطه تکین وجود دارد: «نقاط تکین منفرد» (Isolated Singular Points) و «نقاط انشعاب» (Branch Points).
نقاط تکین منفرد
اگر $$ f ( z ) $$ در هر جایی از همسایگی نقطه $$ z = a $$ (یعنی دایره $$ \mathcal { C } : | z - a | = R $$) به جز خود نقطه $$ z = a $$ تحلیلی باشد، آنگاه $$ z = a $$ یک نقطه تکین منفرد $$ f ( z ) $$ نامیده میشود. تابع $$ f ( z ) $$ نمیتواند در نزدیکی یک نقطه تکین منفرد کراندار باشد.
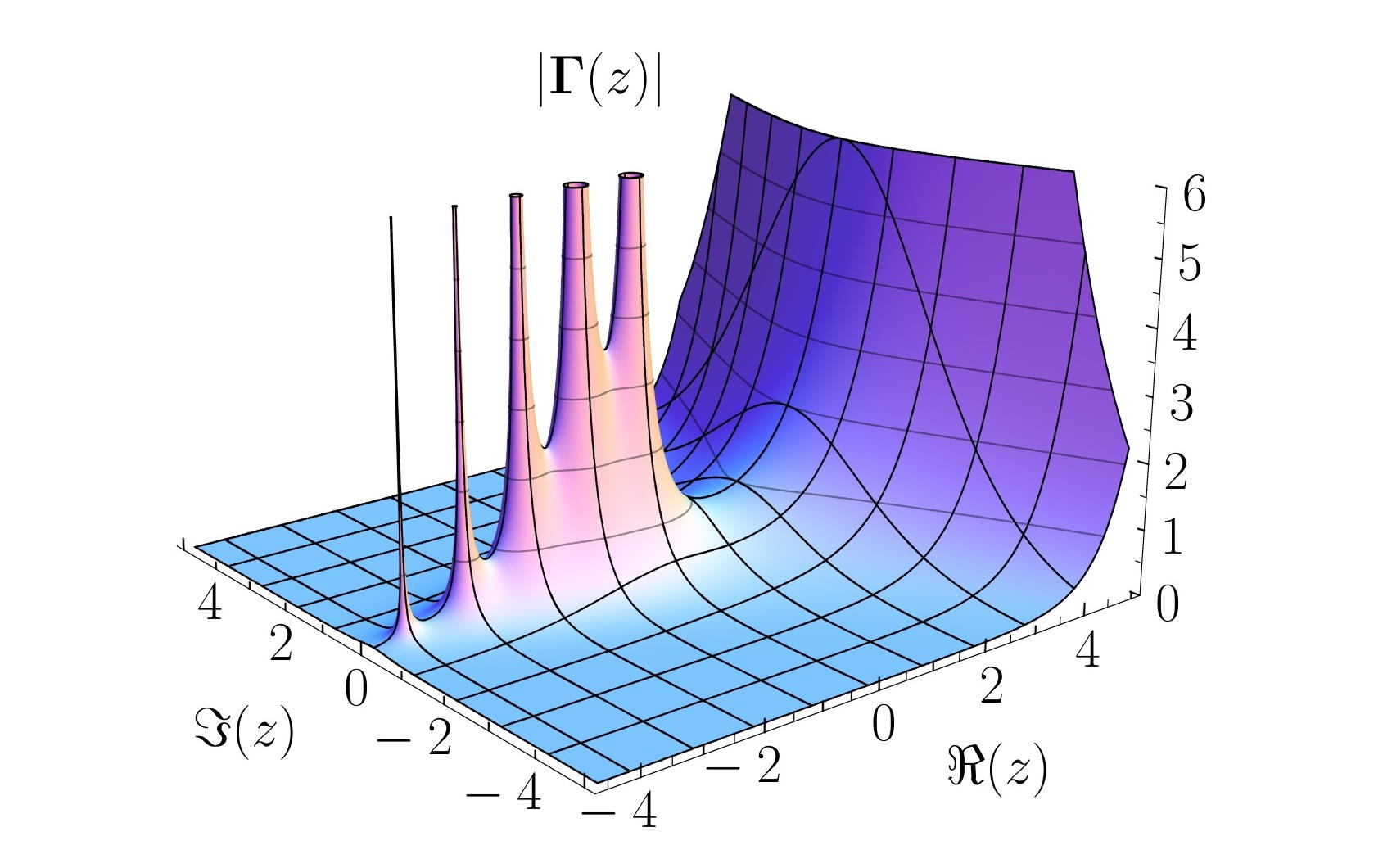
قطبها
اگر $$ f ( z ) $$ دارای یک نقطه تکین منفرد در $$ z = a $$ باشد، یعنی $$ f ( z ) $$ در $$ z = a $$ محدود نباشد، و علاوه بر این، عدد صحیح $$ n $$ به گونهای وجود داشته باشد که $$ ( z - a ) ^ n f ( z ) $$ در $$ z = a $$ تحلیلی باشد، آنگاه $$ f ( z ) $$ یک قطب مرتبه $$ n $$ در $$ z = a $$ دارد ($$ n $$ کوچکترین عدد صحیح است). توجه کنید از آنجا که $$ ( z - a ) ^ n f ( z ) $$ در $$ z = a $$ تحلیلی است، این تکینگی، یک تکینگی برداشتنی (Removable Singularity) نامیده میشود. برای مثال، $$f ( z ) = 1 / z ^ 2$$ یک قطب مرتبه ۲ در $$ z = 0 $$ دارد.
تکینگیهای اساسی
یک نقطه تکین منفرد که یک قطب (تکینگی برداشتنی) نیست، نقطه تکین اساسی نامیده میشود. برای مثال، $$ f ( z ) = \sin ( 1 / z ) $$ یک تکینگی اساسی در $$ z = 0 $$ دارد.
نقاط انشعاب
وقتی $$ f ( z ) $$ یک تابع چندمتغیره باشد، هر نقطهای که نتواند نقطه درونی ناحیه تعریف یک انشعاب تکمقداره از $$ f ( z ) $$ باشد، یک نقطه انشعاب تکین است. برای مثال، $$ f ( z ) = \sqrt { z - a } $$ یک نقطه انشعاب در $$ z = a $$ دارد.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش ریاضیات مهندسی
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- آموزش ریاضیات مهندسی (مرور – تست کنکور ارشد)
- فراکتال چیست؟ — به زبان ساده
- توان و ریشه اعداد مختلط — از صفر تا صد
- فرم نمایی و قطبی اعداد مختلط — به زبان ساده
^^











خوب بود بسیار جای تشکر دارم