انتگرال سطحی – از صفر تا صد (+ دانلود فیلم آموزش گام به گام)
در راستای ارائه مفاهیم مرتبط با انتگرال در وبلاگ فرادرس، در این مطلب قصد داریم مفاهیم و روشهای محاسبه انتگرال روی سطح یا انتگرال سطحی را توضیح دهیم. بهمنظور یادگیری مفهوم انتگرالِ روی سطح، در ابتدا بایستی با بیان پارامتری صفحه و همچنین مشتق آن آشنا باشید. لذا پیشنهاد میشود در ابتدا دو قسمت ابتدای این مطلب را به دقت و با حوصله مطالعه فرمایید.
بیان پارامتری یک صفحه
در مطلب توابع چند متغیره مفهوم توابع دو متغیره عنوان شد. در آنجا گفته شد که یک تابع دومتغیره را میتوان به دو صورت یا بیان کرد (البته در بیان اول میتوان x یا y را نیز به عنوان متغیر وابسته در نظر گرفت). اما یک تابع دو متغیره یا حتی سه متغیره، به صورت پارامتری نیز قابل بیان است.
در حقیقت فرض میشود از مرکز به هر نقطه از صفحهی سهبعدی برداری همچون رسم شود. با بیان کردن بردار مذکور، به صورت پارامتری، صفحهی سهبعدی توصیف میشود. برای نمونه میدانیم که رابطه صفحهای مخروطی شکل به صورت زیر است.

حال تصور کنید صفحه فوق، با استفاده از بردار توصیف شود. بدیهی است که این بردار سهبعدی بوده و بایستی دارای سه مولفه باشد. در حقیقت رابطه کلی این بردار بهصورت زیر است.

اما وابستگی هریک از متغیرها بایستی به نحوی باشد که رابطه بین آنها برقرار باشد. در ابتدا وابستگی x را به صورت x=u در نظر بگیرید. در این صورت با فرض کردن y=u cos v و z=u sin v، میتوان گفت:
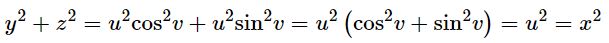
بنابراین بردار فرض شده، سطح سهبعدی S را توصیف میکند. توجه داشته باشید که در نمونهی فوق، صفحه (u,v) به صفحهی سهبعدی S تبدیل شده است. در ادامه بردارها را به صورت بیان میکنیم.
مثال ۲
رابطهی مربوط به بردار پارامتری زیر را بدست آورید.
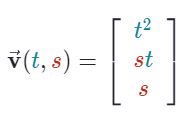
بدیهی است که مولفههای بردار، متناظر با (x,y,z) هستند. بنابراین x=t2 و y=st و z=s هستند. با توجه به این سه عبارت، رابطه زیر را میتوان بین مولفههای بردار v نوشت:
توجه داشته باشید که تبدیل فوق، در حقیقت صفحهای با مختصات (u,v) را به صفحه S تبدیل میکند.
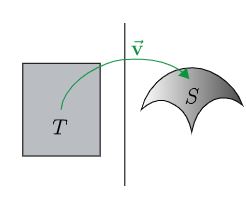
مشتق جزئیِ تابع پارامتری
مثال ۲ را در نظر بگیرید. فرض کنید سطحی که قصد ما تصویر کردن آن است، در بازه زیر محدود شده باشد. سطح مذکور در ادامه ترسیم شده است.
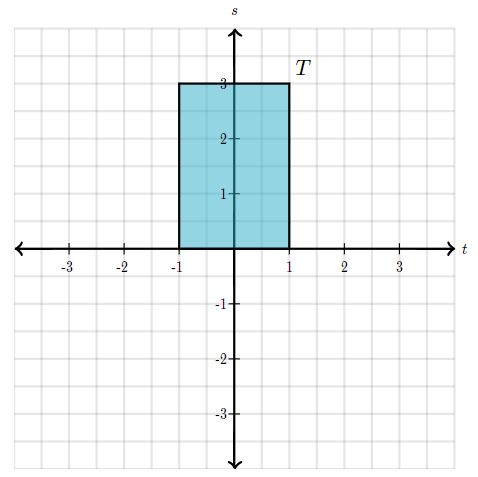
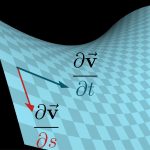
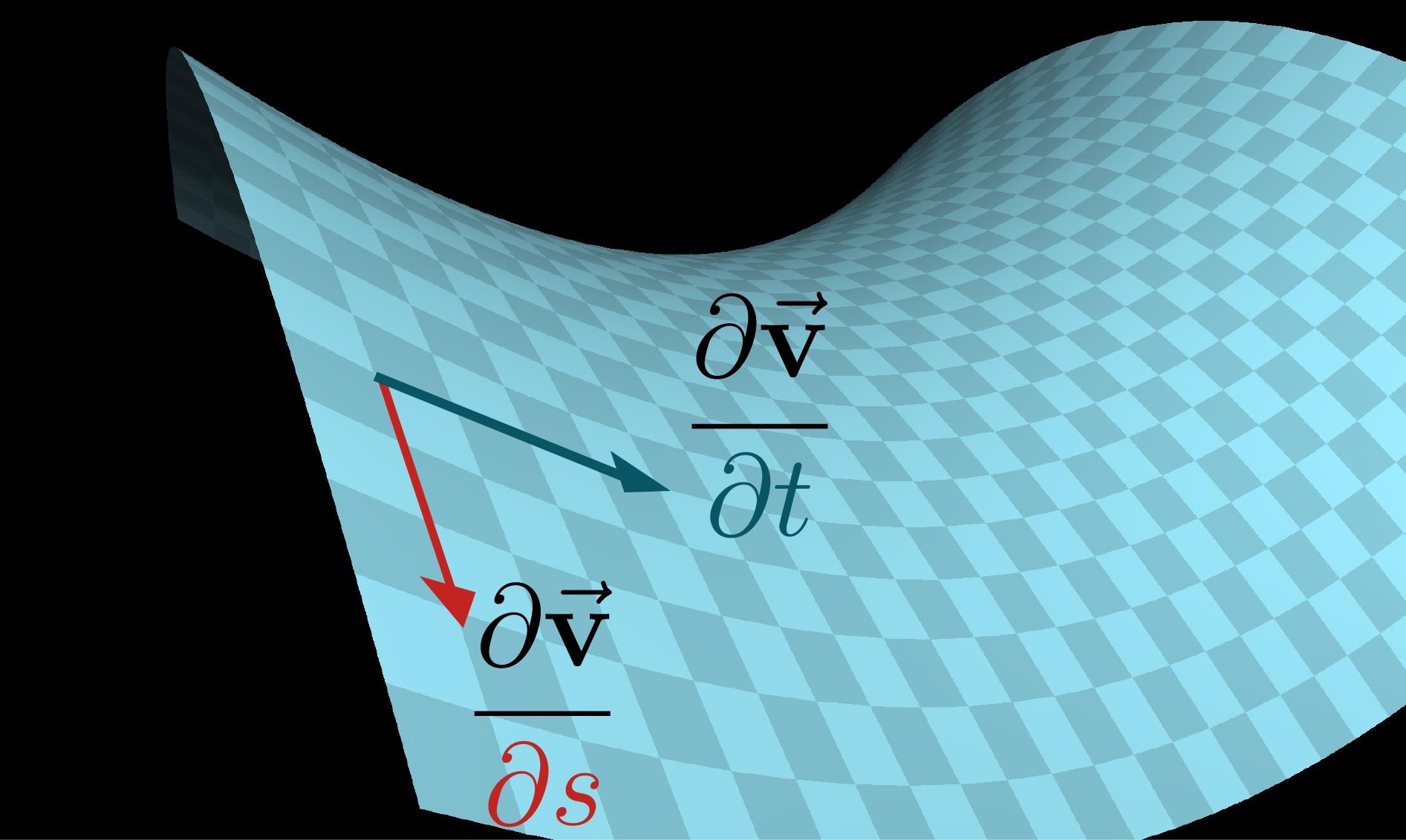
فرض کنید این سطح با نماد T، نامگذاری شود. بدیهی است که این سطح دوبعدی است. هدف ما محاسبه سطح تصویر شدهی T است (سطح تصویر شده T همان سطح سهبعدی S است). بدین منظور در ابتدا مساحت دیفرانسیل سطح را روی صفحه T پیدا کرده و آن را تصویر میکنیم. مطابق با شکل فوق، مساحت دیفرانسیل سطحِ T برابر با ds×dt است.
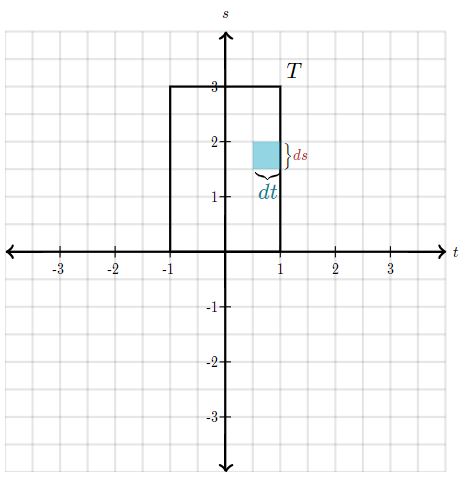
حال سئوال این است که نگاشت به چه صورت این جزء را به جزئی در صفحه S تبدیل میکند؟ در حقیقت با استفاده از این تبدیل، دیفرانسیل مساحت، مطابق با شکل زیر، به دیفرانسیل dS تبدیل میشود.
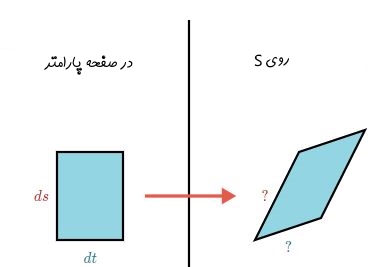
بردار dt به و بردار ds به تبدیل میشود.
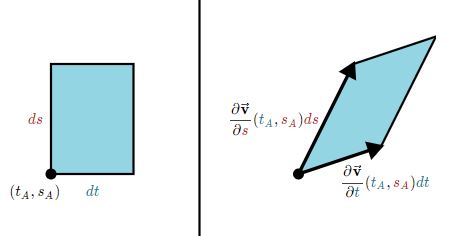
با توجه به تعریف ضرب خارجی، اندازه مساحت دیفرانسیلی سطح S را میتوان برابر با اندازه ضرب خارجی دو بردار تصویر شده در نظر گرفت. بنابراین مساحت dS برابر است با (در آنجا بیان شد که اندازه حاصلضرب خارجی دو بردار برابر با مساحت متوازیالاضلاعی است که دو بردار مذکور ایجاد میکنند):
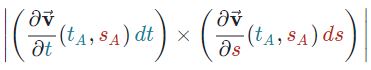
توجه داشته باشید که رابطه فوق مساحت دیفرانسیل قرار گرفته در (tA,sA) را به ما میدهد. برای بدست آوردن کل مساحت، بایستی از رابطه فوق انتگرال بگیریم. در نتیجه کلِ مساحت S را میتوان با استفاده از رابطه زیر بدست آورد.
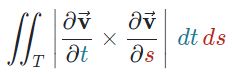
بنابراین مساحت سطوح سهبعدی را میتوان با استفاده از رابطه فوق بدست آورد. البته لازمهی استفاده از ابزار فوق این است که سطح مد نظر به صورت پارامتری بیان شود. در ادامه از مفاهیم بیان شده در بالا استفاده خواهد شد.
نماد انتگرال سطحی
حال با یادگیری نحوه بیان یک سطح سهبعدی، به صورت پارامتری، میتوانید انتگرال هر تابعی را روی سطح مد نظر بدست آورید. پیشتر در وبلاگ فرادرس مفهوم انتگرال دوگانه را بیان کردیم. در آنجا توضیح دادیم که انتگرال دوگانه از صفحهای سهبعدی گرفته شده و بازههای انتگرال روی سطحی دو بعدی تعریف میشود. در شکل زیر ناحیه مد نظر برای یک انتگرال دوگانه نشان داده شده است (ناحیه R).
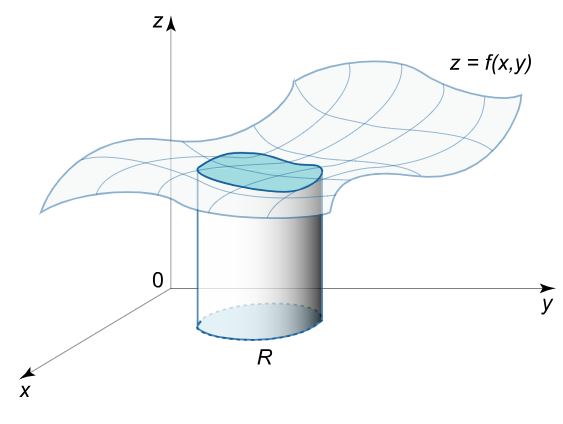
همانطور که در تصویر فوق نیز نشان داده شده، صفحهای که روی آن انتگرال گرفته شده، به صورت سه بعدی بوده و ناحیهی انتگرالگیری، دوبعدی است.
در اصل ایدهی انتگرال روی سطح نیز مشابه با انتگرال دوگانه است. تنها تفاوت این است که ناحیهی انتگرالگیری روی صفحهی سهبعدی قرار میگیرد. به همین دلیل نمادهای استفاده شده برای انتگرال سطح، بسیار مشابه با انتگرال دوگانه است. در حقیقت انتگرال سطحی را به صورت زیر نمایش میدهند.
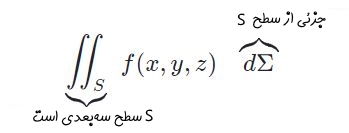
محاسبه انتگرال سطحی دقیقا مشابه با فرمول انتگرال دوگانه است و تنها تفاوت آنها قرار گرفتن یک عبارت در انتگرال است:
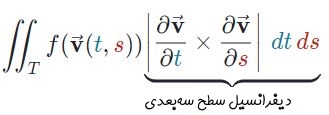
در رابطه فوق، شکل پارامتری شدهی سطح S است.
ایده انتگرال روی سطح
در بالا نحوه بدست آوردن مساحت یک سطح بیان شد. اما در مثالی که در ادامه ذکر شده، یک گام فراتر رفته و کاربرد مهمتری از بیان پارامتری یک سطح را توضیح میدهیم. انتگرالی دوگانه را مطابق با رابطه زیر در نظر بگیرید.
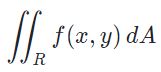
در رابطه فوق، R که همان ناحیه دوبعدی است میتواند سطح فلز و برابر با چگالی آن در مختصات (x,y) باشد. با محاسبه انتگرال فوق، جرم فلز بدست خواهد آمد.

در سناریویی دیگر R میتواند سطح جغرافیایی و برابر با دما در هر نقطه از آن باشد. در این صورت با محاسبه انتگرال فوق و تقسیم آن به کل مساحت، میانگین دمای کل منطقه بدست خواهد آمد.
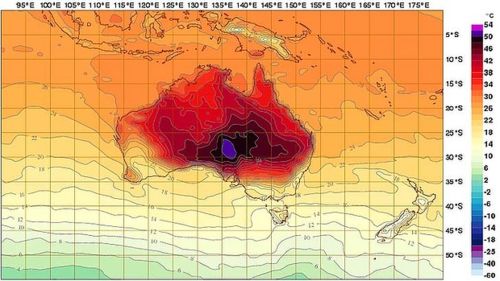
در هر دو نمونه ذکر شده در فوق، سطح فلز و منطقه جغرافیایی به صورت صاف در نظر گرفته شده بودند. حال فرض کنید سطح فلز، بال هواپیما باشد. چطور میتوان با استفاده از انتگرال دوگانه، جرم بال را بدست آورد؟ بدیهی است که در مسئلهی بال هواپیما سطح R، سهبعدی بوده و محاسبه انتگرال دوگانه روی آن دشوار خواهد بود. در این حالت نیز جرم بال با استفاده از رابطه زیر بدست خواهد آمد.
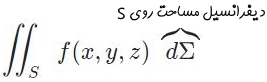
به رابطهی فوق انتگرال روی سطح گفته میشود. نماد S بیانکننده سطحی سهبعدی است که انتگرال روی آن گرفته میشود. در رابطه فوق هریک از اجزای سطحِ سهبعدی S، محاسبه شده و در تابع ضرب میشود. شاید این سوال برایتان پیش آمده باشد که تفاوت دو نماد و در چیست؟ پاسخ در نوع این سطوح است. در حقیقت هر دوی آنها نشان دهنده دیفرانسیل سطح هستند؛ اما نشان دهنده سطحی سهبعدی و dA سطحی دوبعدی را نمایش میدهد.
بدست آوردن انتگرال سطح
برای بدست آوردن انتگرالِ سطح، بایستی در ابتدا سطح S بهصورت دوبعدی بیان شود. سپس با استفاده از روابط ارائه شده در بخش اول این مطلب، دیفرانسیل سطح بهصورت دوبعدی بیان شده و از آن انتگرال گرفته میشود. توجه داشته باشید که بازهی انتگرال در این حالت، بازههای تعریف شدهی s و t هستند. در حقیقت در این حالت سطح سهبعدیِ S، با استفاده از سطح دوبعدی T نشان داده میشود. نهایتا حاصل انتگرالِ روی سطح بهصورت زیر قابل محاسبه میشود.
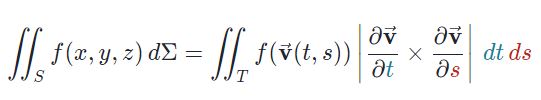
سخن را کوتاه کرده و پیشنهاد میکنیم به مثالهای زیر توجه فرمایید.
مثال ۳
حاصل انتگرال تابع زیر را روی کرهای به شعاع ۲ بیابید.
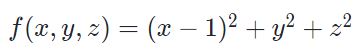
بدیهی است که کرهای به شعاع ۲، سطحی سهبعدی محسوب میشود. بنابراین برای محاسبه انتگرال مرتبط با آن، بایستی از مفهوم انتگرال روی سطح استفاده کرد. رابطهی مربوط به کرهای به شعاع ۲ بهصورت زیر است.
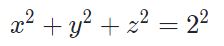
توجه داشته باشید که با توجه به مشابه بودن تابع و معادلهی سطح S، میتوان از تشابه آنها استفاده کرده و عبارت زیر انتگرال را سادهتر کرد. با باز کردن تابع f داریم:

لازم است بدانید که رابطهی فوق در تمامی نقاط صادق نیست؛ در حقیقت تنها در نقاطی که روی سطح S قرار دارند، رابطه مذکور برقرار است. در این مسئله نیز انتگرال روی این سطح محاسبه میشود، بنابراین میتوان از رابطه بالا استفاده کرد. نهایتا انتگرال مد نظر برای محاسبه را میتوان به شکل زیر بیان کرد:
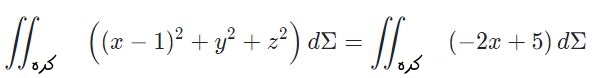
بهمنظور برقراری ارتباط میان انتگرال فوق و انتگرال دوگانه، بایستی سطح کره را به صورت پارامتری بیان کرد. بدین منظور، بردار را به صورت زیر بیان میکنیم.
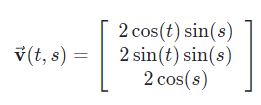
البته توجه داشته باشید که t در بازهی و s در بازهی قرار دارند. در مرحلهی بعد بایستی با توجه به بردار تعریف شدهی v، عبارت زیر را برای آن محاسبه کرد.
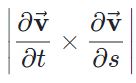
مشتق v نسبت به پارامترهای t و s بهترتیب برابرند با:
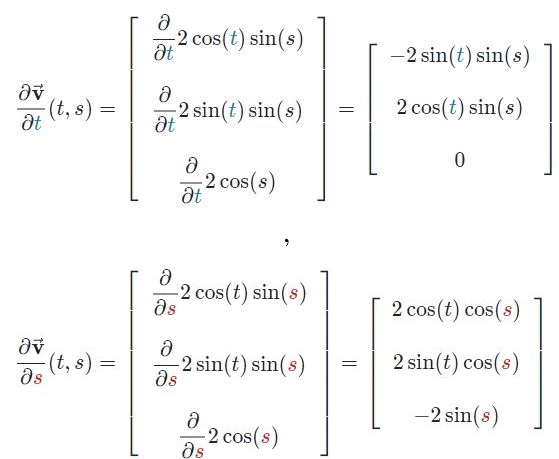
حال میتوان حاصلضرب خارجی را به صورت زیر بدست آورد.
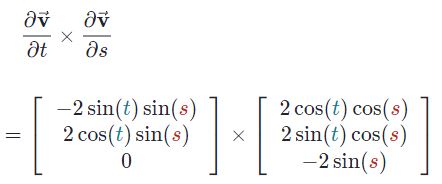
ضرب خارجی فوق را میتوان برابر با دترمینان ماتریس زیر در نظر گرفت.
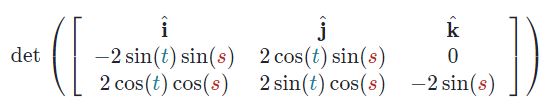
مولفهی ، به صورت زیر بدست میآید.
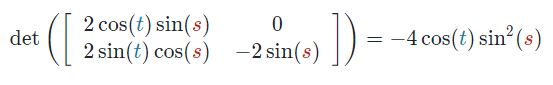
به همین صورت مولفههای و نیز برابرند با:

با بدست آمدن مولفههای بردار ، اندازهی آن به صورت زیر بدست میآید.
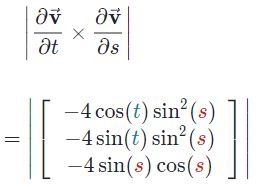
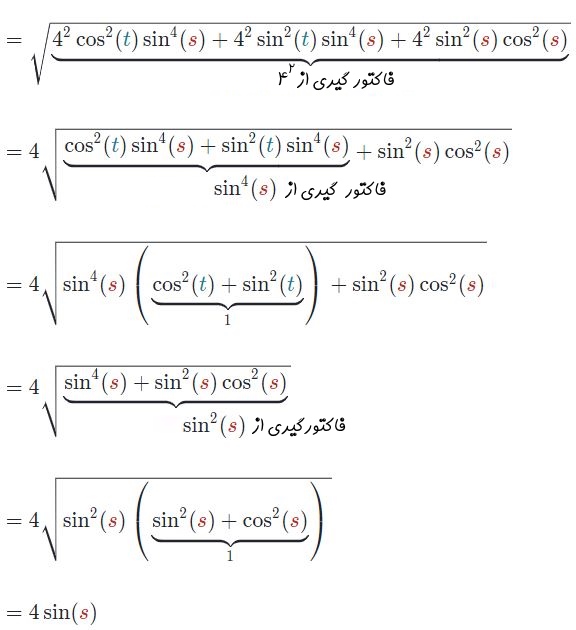
تا این مرحله تمامی اجزای لازم بهمنظور محاسبه انتگرال روی سطح بدست آمد. نهایتا حاصل انتگرال روی سطح برابر است با:
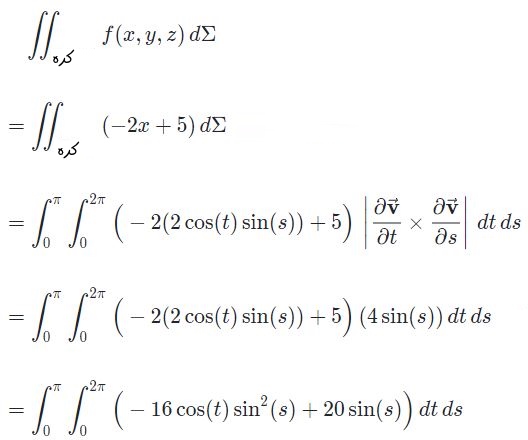
حاصل بخشی از انتگرال مطابق با روابط زیر، برابر با صفر بدست میآید.

بخش دوم انتگرال نیز برابر است با:
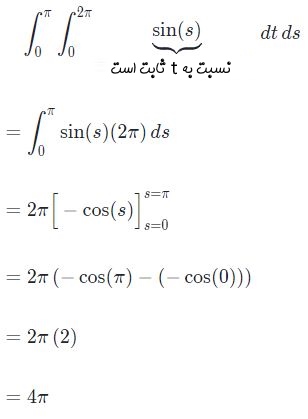
نهایتا حاصل انتگرال سطح، برابر است با:
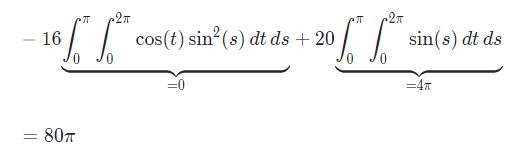
مراحل توضیح داده شده در بالا به تفکیک ارائه شده، لذا زمان حل به نظر طولانی رسیده است. البته در اکثر سوالات انتگرال روی سطح، تابع تحت انتگرال ساده شده و زمان حل کوتاه میشود.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضیات، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضی
- مجموعه آموزشهای ریاضی و فیزیک
- قضیه گرین -- به زبان ساده
- انتگرال دوگانه — به زبان ساده
- معادله لاپلاس — از صفر تا صد
- انتگرال توابع مثلثاتی — از صفر تا صد
^^













سلام و احترام؛
کاش بجای اینکه از «فرمول» شروع کنید، از منطق و خصوصاً «ایدهٔ» اصلی که قراره باهاش بعداً به فرمول برسیم شروع میکردید.
با اینکه زحمت کشیدهاید و وقت گذاشتهاید و نسبتاً مفصّل برگزار کردهاید، اما بخاطر عدم توضیح ایدهٔ اصلی و رویکردِ اصلی در حل این دسته از مسائل، برای این دوست کوچکتون ثمربخش نبود.
با سپاس.
با سلام؛
از بازخورد شما بسیار سپاسگزاریم. سعی بر این است که ابتدا به پرسش مخاطب پاسخ دهیم و سپس اطلاعات بیشتر و پایهایتری نیز در اختیار او قرار دهیم.
با تشکر از همراهی شما با مجله فرادرس
خیلی ممنون
اینکه اول هر مطلب پیش نیاز ها رو لینک میکنید خیلی عالیه
در کل من تمام اموزشهای فرادرس رو پیگیرم
خسته نباشید و خدا قوت
امیدوارم همچنان ادامه بدید
با سلام
لطفا میشه توضیح بدید در مثال 3 مولفه های ماتریس توابع پارامتری بردار v چطوری به دست اومدن؟ و همچنین محدوده های هر کدوم! چرا یکی تا پی هست؟!
با سلام.
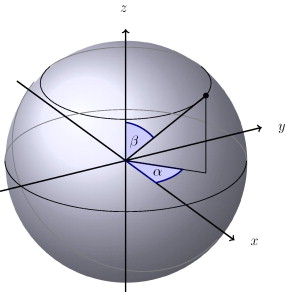
در ابتدا پیشنهاد میکنیم جهت درک بهتر مطلب مختصات کروی را مطالعه فرمایید.
مطابق با شکل زیر اگر شما حول محور z به اندازه 2π بچرخید، یک دایره بدست خواهد آمد. حال این دایره را حول یکی از محورهای x یا y به اندازه π دوران دهید. در این صورت کره مد نظر یا همان سطح انتگرالگیری بدست میآید. بنابراین عدد π نشان دهنده دوران دوم است.