در آموزشهای قبلی از مجموعه آموزشهای ریاضیات مجله فرادرس، درباره خط مماس و قائم بر منحنی و انحنا و شعاع انحنای منحنیها بحث کردیم. در این آموزش، منحنی بوسان و دایره بوسان را همراه با چند مثال حل شده معرفی خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
مرتبه یا درجه تماس خمهای مسطح
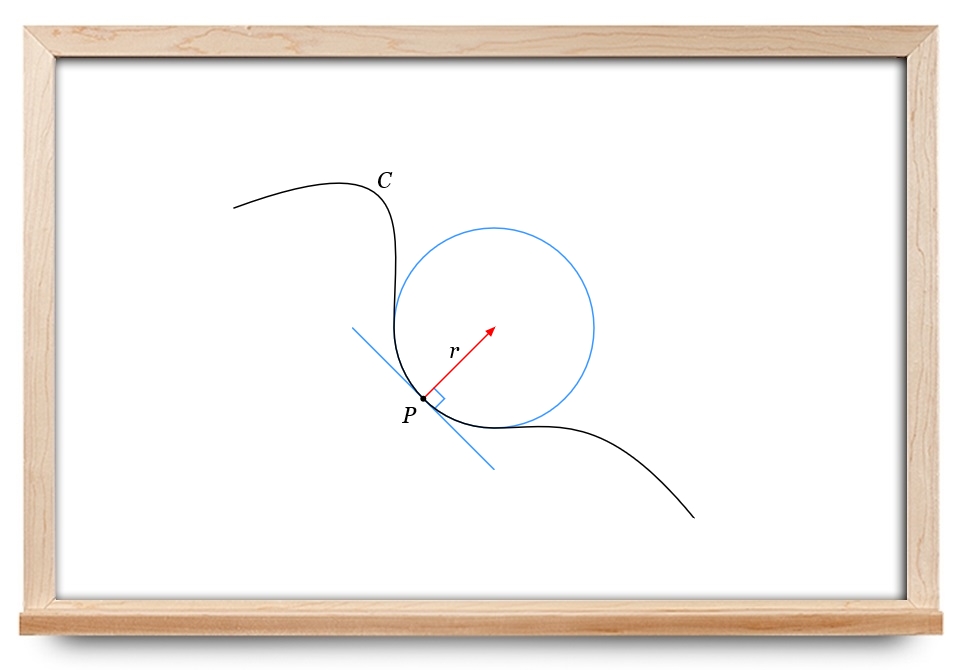
فرض کنید y = f ( x ) y = f\left( x \right) y = f ( x ) y = g ( x ) y = g\left( x \right) y = g ( x ) M 0 ( x 0 , y 0 ) {M_0}\left( {{x_0},{y_0}} \right) M 0 ( x 0 , y 0 ) ( n + 1 ) (n+1 ) ( n + 1 )
شکل ۱ دو منحنی y = f ( x ) y = f\left( x \right) y = f ( x ) y = g ( x ) y = g\left( x \right) y = g ( x ) M 0 ( x 0 , y 0 ) {M_0}\left( {{x_0},{y_0}} \right) M 0 ( x 0 , y 0 ) n n n
f ( x 0 ) = g ( x 0 ) , f ’ ( x 0 ) = g ’ ( x 0 ) , f ′ ′ ( x 0 ) = g ′ ′ ( x 0 ) , … , f ( n ) ( x 0 ) = g ( n ) ( x 0 ) , f ( n + 1 ) ( x 0 ) ≠ g ( n + 1 ) ( x 0 ) . \large \begin {align*} f \left ( { { x _ 0 } } \right ) & = g \left ( { { x _ 0 } } \right ) , \; \; \; \kern-0.3pt \\ f ’ \left ( { { x _ 0 } } \right ) & = g ’ \left ( { { x _ 0 } } \right ) , \; \; \; \kern-0.3pt \\ f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) & = g ^ { \prime \prime } \left ( { { x _ 0 } } \right ) , \\ & \ldots , \; \; \; \kern-0.3pt \\ { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) & = { g ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) , \; \; \; \kern-0.3pt \\ { f ^ { \left ( { n + 1 } \right ) } } \left ( { { x _ 0 } } \right ) & \ne { g ^ { \left ( { n + 1 } \right ) } } \left ( { { x _ 0 } } \right ) . \end{align*} f ( x 0 ) f ’ ( x 0 ) f ′′ ( x 0 ) f ( n ) ( x 0 ) f ( n + 1 ) ( x 0 ) = g ( x 0 ) , = g ’ ( x 0 ) , = g ′′ ( x 0 ) , … , = g ( n ) ( x 0 ) , = g ( n + 1 ) ( x 0 ) .
به طور خاص اگر n = 1 n = 1 n = 1 y = f ( x ) y = f\left( x \right) y = f ( x ) y = g ( x ) y = g\left( x \right) y = g ( x ) خط مماس مشترک دارند.
حالت n = 0 n = 0 n = 0 M 0 ( x 0 , y 0 ) {M_0}\left( {{x_0},{y_0}} \right) M 0 ( x 0 , y 0 ) f ( x 0 ) = g ( x 0 ) f\left( {{x_0}} \right) = g\left( {{x_0}} \right) f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) ≠ g ’ ( x 0 ) f’\left( {{x_0}} \right) \ne g’\left( {{x_0}} \right) f ’ ( x 0 ) = g ’ ( x 0 ) M 0 M_0 M 0
میتوانیم تفاضل بین توابع φ ( x ) = g ( x ) – f ( x ) \varphi \left( x \right) = g\left( x \right) – f\left( x \right) φ ( x ) = g ( x ) – f ( x ) x 0 x _ 0 x 0 بسط تیلور آن را با فرم پئانو (Peano’s Form) باقیمانده بنویسیم. اگر منحنیهای g ( x ) g (x) g ( x ) f ( x ) f (x) f ( x ) n n n n n n φ ( x ) \varphi \left( x \right) φ ( x )
φ ( x ) = φ ( n + 1 ) ( x 0 ) + α ( n + 1 ) ! ( x – x 0 ) n + 1 = g ( n + 1 ) ( x 0 ) – f ( n + 1 ) ( x 0 ) + α ( n + 1 ) ! ⋅ ( x – x 0 ) n + 1 \large \begin {align*} \varphi \left ( x \right ) & = \frac { { { \varphi ^ { \left ( { n + 1 } \right ) } } \left ( { { x _ 0 } } \right ) + \alpha } } { { \left ( { n + 1 } \right ) ! } } { \left ( { x – { x _ 0 } } \right ) ^ { n + 1 } } \\ & = { \frac { { { g ^ { \left ( { n + 1 } \right ) } } \left ( { { x _ 0 } } \right ) – { f ^ { \left ( { n + 1 } \right ) } } \left ( { { x _ 0 } } \right ) + \alpha } } { { \left ( { n + 1 } \right ) ! } } \cdot } \kern0pt { { \left ( { x – { x _0 } } \right ) ^ { n + 1 } } } \end{align*} φ ( x ) = ( n + 1 ) ! φ ( n + 1 ) ( x 0 ) + α ( x – x 0 ) n + 1 = ( n + 1 ) ! g ( n + 1 ) ( x 0 ) – f ( n + 1 ) ( x 0 ) + α ⋅ ( x – x 0 ) n + 1
که با ( x – x 0 ) n + 1 {\left( {x – {x_0}} \right)^{n + 1}} ( x – x 0 ) n + 1 n n n φ ( x ) \varphi \left( x \right) φ ( x ) M 0 M_0 M 0 n = 0 n = 0 n = 0
برای n n n y = f ( x ) y = f\left( x \right) y = f ( x ) y = g ( x ) y = g\left( x \right) y = g ( x ) M 0 M_0 M 0
منحنی بوسان
فرض کنید معادله منحنی y = f ( x ) y = f\left( x \right) y = f ( x ) G ( x , y , a , b , … , ℓ ) = 0 G\left( {x,y,a,b, \ldots ,\ell} \right) = 0 G ( x , y , a , b , … , ℓ ) = 0 n + 1 n + 1 n + 1 a a a b b b … \ldots … l l l y = f ( x ) y = f (x ) y = f ( x ) M 0 ( x 0 , y 0 ) {M_0}\left( {{x_0},{y_0}} \right) M 0 ( x 0 , y 0 )
نمایش زیر را در نظر بگیرید:
Φ ( x , a , b , … , l ) = G ( x , f ( x ) , a , b , … , l ) . \large \Phi \left ( { x , a , b , \ldots , l } \right ) = G \left ( { x , f \left ( x \right ) , a , b , \ldots , l } \right ) . Φ ( x , a , b , … , l ) = G ( x , f ( x ) , a , b , … , l ) .
شرایط تماس به صورت زیر هستند:
{ Φ ( x 0 , a , b , … , ℓ ) = 0 Φ ’ x ( x 0 , a , b , … , ℓ ) = 0 Φ x x ′ ′ ( x 0 , a , b , … , ℓ ) = 0 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ Φ x n ( n ) ( x 0 , a , b , … , ℓ ) = 0 . \large \left\{ \begin {array} {l} \Phi \left ( { { x _ 0} , a , b , \ldots , \ell } \right ) = 0 \\ { \Phi ’ _ x } \left ( { { x_ 0 } , a , b , \ldots , \ell } \right ) = 0 \\ { \Phi ^ { \prime \prime } _ { x x } } \left ( { { x _ 0 } , a , b , \ldots , \ell } \right ) = 0 \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ \Phi _ { { x ^ n } } ^ { \left ( n \right ) } \left ( { { x _ 0} , a , b , \ldots , \ell } \right ) = 0 \end{array} \right.. ⎩ ⎨ ⎧ Φ ( x 0 , a , b , … , ℓ ) = 0 Φ ’ x ( x 0 , a , b , … , ℓ ) = 0 Φ xx ′′ ( x 0 , a , b , … , ℓ ) = 0 ⋯⋯⋯⋯⋯⋯⋯ Φ x n ( n ) ( x 0 , a , b , … , ℓ ) = 0 .
شرایط بالا، یک دستگاه n + 1 n +1 n + 1 n + 1 n + 1 n + 1 a a a b b b … \ldots … l l l n n n n + 1 n +1 n + 1
دایره بوسان
در این بخش، معادله دایره بوسان را به دست میآوریم. فرض کنید تابع y = f ( x ) y = f (x ) y = f ( x )
( x – a ) 2 + ( y – b ) 2 = R 2 . \large { \left ( { x – a } \right ) ^ 2 } + { \left ( { y – b } \right ) ^ 2 } = { R ^ 2 } . ( x – a ) 2 + ( y – b ) 2 = R 2 .
همانطور که میبینیم، در اینجا سه پارامتر داریم: مختصات a a a b b b R R R 2 2 2
رابطه زیر را داریم:
Φ ( x , a , b , R ) = ( x – a ) 2 + ( y – b ) 2 – R 2 \large { \Phi \left ( { x , a , b , R } \right ) } = { { \left ( { x – a } \right ) ^ 2 } + { \left ( { y – b } \right ) ^ 2 } – { R ^ 2} } Φ ( x , a , b , R ) = ( x – a ) 2 + ( y – b ) 2 – R 2
مشتقات تابع Φ \Phi Φ
Φ ’ x ( x 0 , a , b , R ) = 2 ( x – a ) + 2 ( y – b ) y ’ , Φ x x ′ ′ ( x 0 , a , b , R ) = 2 + 2 ( y ’ ) 2 + 2 ( y – b ) y ′ ′ . \large \begin {align*} { { \Phi ’ _ x } \left ( { { x _ 0 } , a , b , R } \right ) } & = { 2 \left ( { x – a } \right ) + 2 \left ( { y – b } \right ) y ’ , } \; \; \; \kern-0.3pt \\ { { \Phi ^ { \prime \prime } _ { x x } } \left ( { { x _ 0 } , a , b , R } \right ) } & = { 2 + 2 { \left ( { y ’ } \right ) ^ 2 } + 2 \left ( { y – b } \right ) y ^ { \prime \prime } . } \end{align*} Φ ’ x ( x 0 , a , b , R ) Φ xx ′′ ( x 0 , a , b , R ) = 2 ( x – a ) + 2 ( y – b ) y ’ , = 2 + 2 ( y ’ ) 2 + 2 ( y – b ) y ′′ .
با فرض اینکه منحنیها در نقطه ( x 0 , y 0 ) \left( {{x_0},{y_0}} \right) ( x 0 , y 0 ) دستگاه سه معادلهای زیر را برای پیدا کردن دایره بوسان به دست میآوریم:
{ Φ ( x 0 , a , b , R ) = 0 Φ ’ x ( x 0 , a , b , R ) = 0 Φ x x ′ ′ ( x 0 , a , b , R ) = 0 , ⇒ { ( x 0 – a ) 2 + ( y 0 – b ) 2 – R 2 = 0 2 ( x 0 – a ) + 2 ( y 0 – b ) y ’ 0 = 0 2 + 2 ( y ’ 0 ) 2 + 2 ( y 0 – b ) y 0 ′ ′ = 0 \large { \left\{ \begin {array} { l } \Phi \left ( { { x _ 0 } , a , b , R } \right ) = 0 \\ { \Phi ’ _ x } \left ( { { x _ 0 } , a , b , R } \right ) = 0 \\ { \Phi ^ { \prime \prime } _ { x x } } \left ( { { x _ 0 } , a , b , R } \right ) = 0 \end {array} \right . , \; \; } \Rightarrow { \left\{ \begin {array} { l } { \left ( { { x _ 0 } – a } \right ) ^ 2 } + { \left ( { { y _ 0 } – b } \right ) ^ 2 } – { R ^ 2 } = 0 \\ 2 \left ( { { x _ 0 } – a } \right ) + 2 \left ( { { y _ 0 } – b } \right ) { y ’ _ 0 } = 0 \\ 2 + 2 \left ( { { y ’ _ 0 } } \right ) ^ 2 + 2 \left ( { { y _ 0} – b } \right ) { y ^ { \prime \prime } _ 0 } = 0 \end {array} \right . } ⎩ ⎨ ⎧ Φ ( x 0 , a , b , R ) = 0 Φ ’ x ( x 0 , a , b , R ) = 0 Φ xx ′′ ( x 0 , a , b , R ) = 0 , ⇒ ⎩ ⎨ ⎧ ( x 0 – a ) 2 + ( y 0 – b ) 2 – R 2 = 0 2 ( x 0 – a ) + 2 ( y 0 – b ) y ’ 0 = 0 2 + 2 ( y ’ 0 ) 2 + 2 ( y 0 – b ) y 0 ′′ = 0
از معادله آخر میتوان مقدار b b b
2 + 2 ( y ’ 0 ) 2 + 2 ( y 0 – b ) y 0 ′ ′ = 0 , ⇒ ( y 0 – b ) y 0 ′ ′ = – 1 – ( y ’ 0 ) 2 , ⇒ y 0 – b = – 1 + ( y ’ 0 ) 2 y 0 ′ ′ , ⇒ b = y 0 + 1 + ( y ’ 0 ) 2 y 0 ′ ′ . \large 2 + 2 { \left ( { { y ’ _ 0 } } \right ) ^ 2 } + 2 \left ( { { y _ 0 } – b } \right ) { y ^ { \prime \prime } _ 0 } = 0 , \; \; \Rightarrow { \left ( { { y _ 0 } – b } \right ) { y ^ { \prime \prime } _ 0 } = – 1 – { \left ( { { y ’ _ 0 } } \right ) ^ 2 } , \; \; } \\ \large \Rightarrow { { y _ 0 } – b = – \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y^ { \prime \prime } _ 0 } } } , \; \; } \Rightarrow { b = { y _ 0 } + \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } }{ { { y ^ { \prime \prime } _ 0 } } } . } 2 + 2 ( y ’ 0 ) 2 + 2 ( y 0 – b ) y 0 ′′ = 0 , ⇒ ( y 0 – b ) y 0 ′′ = –1– ( y ’ 0 ) 2 , ⇒ y 0 – b = – y 0 ′′ 1 + ( y ’ 0 ) 2 , ⇒ b = y 0 + y 0 ′′ 1 + ( y ’ 0 ) 2 .
با جایگذاری y 0 – b {{y_0} – b} y 0 – b a a a
2 ( x 0 – a ) + 2 ( y 0 – b ) y ’ 0 = 0 , ⇒ x 0 – a = – ( y 0 – b ) y ’ 0 , ⇒ x 0 – a = 1 + ( y ’ 0 ) 2 y 0 ′ ′ y ’ 0 , ⇒ a = x 0 – 1 + ( y ’ 0 ) 2 y 0 ′ ′ y ’ 0 . \large { 2 \left ( { { x _ 0 } – a } \right ) + 2 \left ( { { y _ 0 } – b } \right ) { y ’ _ 0 } = 0 , \; \; } \Rightarrow { { x _ 0 } – a = – \left ( { { y _ 0 } – b } \right ) { y ’ _ 0 } , \; \; } \\ \large \Rightarrow { { x _ 0 } – a = \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y ^ { \prime \prime } _ 0 } } } { y ’ _ 0 } , \; \; } \Rightarrow { a = { x _ 0 } – \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } {{ { y ^ { \prime \prime } _ 0 } } } { y ’ _ 0 } . } 2 ( x 0 – a ) + 2 ( y 0 – b ) y ’ 0 = 0 , ⇒ x 0 – a = – ( y 0 – b ) y ’ 0 , ⇒ x 0 – a = y 0 ′′ 1 + ( y ’ 0 ) 2 y ’ 0 , ⇒ a = x 0 – y 0 ′′ 1 + ( y ’ 0 ) 2 y ’ 0 .
شعاع دایره بوسان را میتوان از معادله اول تعیین کرد:
( x 0 – a ) 2 + ( y 0 – b ) 2 – R 2 = 0 , ⇒ R 2 = ( x 0 – a ) 2 + ( y 0 – b ) 2 , ⇒ R 2 = ( 1 + ( y ’ 0 ) 2 y 0 ′ ′ y ’ 0 ) 2 + ( 1 + ( y ’ 0 ) 2 y 0 ′ ′ ) 2 , ⇒ R 2 = ( 1 + ( y ’ 0 ) 2 y 0 ′ ′ ) 2 ⋅ [ ( y ’ 0 ) 2 + 1 ] , ⇒ R 2 = [ 1 + ( y ’ 0 ) 2 ] 3 ( y 0 ′ ′ ) 2 , ⇒ R = [ 1 + ( y ’ 0 ) 2 ] 3 2 ∣ y 0 ′ ′ ∣ . \large \begin {align*} & { { \left ( { { x _ 0 } – a } \right ) ^ 2 } + { \left ( {{ y _ 0 } – b } \right ) ^ 2 } – { R ^ 2 } = 0 , \; \; } \\ & \Rightarrow { { R ^ 2 } = { \left ( { { x _ 0 } – a } \right ) ^ 2 } + { \left ( { { y _ 0 } – b } \right ) ^ 2 } , \; \; } \\ & \Rightarrow { { R ^ 2 } = { \left ( { \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y ^ { \prime \prime } _ 0 } } } { y ’ _ 0 } } \right ) ^ 2 } } + { { \left ( { \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y ^ { \prime \prime } _ 0 } } } } \right ) ^ 2 } , \; \; } \\ & \Rightarrow { { R ^ 2 } = { \left ( { \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } {{ { y ^ { \prime \prime } _ 0 } } } } \right ) ^ 2 } \cdot \kern0pt { \left [ { { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } + 1 } \right ] , } \; \; } \\ & \Rightarrow { { R ^ 2 } = \frac { { { { \left [ { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } \right ] } ^ 3 } } } { { { { \left ( { { y ^ { \prime \prime } _ 0 } } \right ) } ^ 2 } } } , \; \; } \\ & \Rightarrow { R = \frac { { { { \left [ { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^2 }} \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { { y ^ { \prime \prime } _ 0 } } \right | } } . } \end{align*} ( x 0 – a ) 2 + ( y 0 – b ) 2 – R 2 = 0 , ⇒ R 2 = ( x 0 – a ) 2 + ( y 0 – b ) 2 , ⇒ R 2 = ( y 0 ′′ 1 + ( y ’ 0 ) 2 y ’ 0 ) 2 + ( y 0 ′′ 1 + ( y ’ 0 ) 2 ) 2 , ⇒ R 2 = ( y 0 ′′ 1 + ( y ’ 0 ) 2 ) 2 ⋅ [ ( y ’ 0 ) 2 + 1 ] , ⇒ R 2 = ( y 0 ′′ ) 2 [ 1 + ( y ’ 0 ) 2 ] 3 , ⇒ R = y 0 ′′ [ 1 + ( y ’ 0 ) 2 ] 2 3 .
میبینیم که مختصات a a a b b b y = f ( x ) y = f (x ) y = f ( x ) x 0 x _0 x 0
مثالها
در ادامه، چند مثال حل شده را بررسی میکنیم.
مثال ۱
منحنی سهمی بوسان با تابع نمایی f ( x ) = e x f\left( x \right) = {e^x} f ( x ) = e x x 0 = 0 x _ 0 = 0 x 0 = 0
حل: فرض میکنیم منحنی با معادله y = g ( x ) = a x 2 + b x + c y = g\left( x \right) = a{x^2} + bx + c y = g ( x ) = a x 2 + b x + c 2 2 2 a a a b b b c c c
{ f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) = g ’ ( x 0 ) f ′ ′ ( x 0 ) = g ′ ′ ( x 0 ) . \large \left\{ \begin {array} { l } f \left ( { { x _ 0 } } \right ) = g \left ( { { x _ 0 } } \right ) \\ f ’ \left ( { { x _ 0 } } \right ) = g ’ \left ( { { x _ 0 } } \right ) \\ f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) = g ^ { \prime \prime } \left ( { { x _ 0 } } \right ) \end{array} \right.. ⎩ ⎨ ⎧ f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) = g ’ ( x 0 ) f ′′ ( x 0 ) = g ′′ ( x 0 ) .
مشتقات توابع f ( x ) = e x f\left( x \right) = {e^x} f ( x ) = e x g ( x ) = a x 2 + b x + c g\left( x \right) = a{x^2} + bx + c g ( x ) = a x 2 + b x + c
f ’ ( x ) = ( e x ) ′ = e x , f ′ ′ ( x ) = ( e x ) ′ = e x ; g ’ ( x ) = ( a x 2 + b x + c ) ′ = 2 a x + b , g ′ ′ ( x ) = ( 2 a x + b ) ′ = 2 a . \large { f ’ \left ( x \right ) = { \left ( { { e ^ x } } \right ) ^ \prime } = { e ^ x } , } \; \; \; \kern-0.3pt { f ^ { \prime \prime } \left ( x \right ) = { \left ( { { e ^ x } } \right ) ^ \prime } = { e ^ x } ; } \\ \large { g ’ \left ( x \right ) = { \left ( { a { x ^ 2 } + b x + c } \right ) ^ \prime } = 2 a x + b , } \; \; \; \kern-0.3pt { g ^ { \prime \prime } \left ( x \right ) = { \left ( { 2 a x + b } \right ) ^ \prime } = 2 a . } f ’ ( x ) = ( e x ) ′ = e x , f ′′ ( x ) = ( e x ) ′ = e x ; g ’ ( x ) = ( a x 2 + b x + c ) ′ = 2 a x + b , g ′′ ( x ) = ( 2 a x + b ) ′ = 2 a .
در نتیجه، دستگاه معادلات به صورت زیر خواهد بود:
{ e x 0 = a x 0 2 + b x 0 + c e x 0 = 2 a x 0 + b e x 0 = 2 a . \large \left\{ \begin {array} { l } { e ^ { { x _ 0 } } } = a x _ 0 ^ 2 + b { x _ 0 } + c \\ { e ^ { { x _ 0 } } } = 2 a { x _ 0 } + b \\ { e ^ { { x _ 0 } } } = 2 a \end{array} \right.. ⎩ ⎨ ⎧ e x 0 = a x 0 2 + b x 0 + c e x 0 = 2 a x 0 + b e x 0 = 2 a .
با قرار دادن x 0 = 0 {x_0} = 0 x 0 = 0
{ c = 1 b = 1 2 a = 1 ≡ { a = 1 2 b = 1 c = 1 . \large \left\{ \begin {array} { l } c = 1 \\ b = 1 \\ 2 a = 1 \end {array} \right. \; \;\kern-0.3pt { \equiv \; \; \left\{ \begin {array} { l } a = \frac { 1 } { 2 } \\ b = 1 \\ c = 1 \end{array} \right..} ⎩ ⎨ ⎧ c = 1 b = 1 2 a = 1 ≡ ⎩ ⎨ ⎧ a = 2 1 b = 1 c = 1 .
بنابراین، سهمی بوسان با تابع نمایی در نقطه x 0 = 0 x _0 = 0 x 0 = 0
y = x 2 2 + x + 1. \large y = \frac { { { x ^ 2 } } } { 2 } + x + 1 . y = 2 x 2 + x + 1.
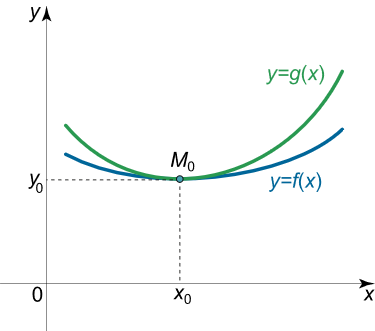
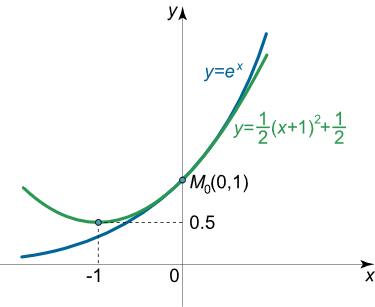
اگر معادله را به فرم زیر بنویسیم، میبینیم که رأس سهمی در نقطه ( – 1 , 1 2 ) \left( { – 1,{\large\frac{1}{2}\normalsize}} \right) ( –1 , 2 1 )
y = x 2 2 + x + 1 = 1 2 ( x 2 + 2 x ) + 1 = 1 2 ( x 2 + 2 x + 1 – 1 ) + 1 = 1 2 ( x + 1 ) 2 + 1 2 \large \begin {align*} y & = \frac { { { x ^ 2 } } } { 2 } + x + 1 = { \frac { 1 } { 2 } \left ( { { x ^ 2 } + 2 x } \right ) + 1 } \\ & = { \frac { 1 } { 2 } \left ( { { x ^ 2 } + 2 x + 1 – 1 } \right ) + 1 } = { \frac { 1 } { 2 } { \left ( { x + 1 } \right ) ^ 2 } + \frac { 1 } { 2 } } \end{align*} y = 2 x 2 + x + 1 = 2 1 ( x 2 + 2 x ) + 1 = 2 1 ( x 2 + 2 x + 1–1 ) + 1 = 2 1 ( x + 1 ) 2 + 2 1
نمودار دو منحنی بوسان در شکل ۲ نشان داده شده است.
شکل ۲ مثال ۲
معادله سهمی بوسان با تابع f ( x ) = cos x f\left( x \right) = \cos x f ( x ) = cos x x 0 = 0 x _0 = 0 x 0 = 0
حل: فرض میکنیم دسته سهمیها سه پارامتر دارند و معادله آنها با سه پارامتر a a a b b b c c c
y = a x 2 + b x + c \large y = a { x ^ 2 } + b x + c y = a x 2 + b x + c
تابع زیر را معرفی میکنیم:
Φ ( x , a , b , c ) = a x 2 + b x + c – f ( x ) \large \Phi \left ( { x , a , b , c } \right) = a { x ^ 2 } + b x + c – f \left ( x \right ) Φ ( x , a , b , c ) = a x 2 + b x + c – f ( x )
شرایط تماس در نقطه x 0 x _0 x 0
{ Φ ( x 0 , a , b , c ) = 0 Φ ’ x ( x 0 , a , b , c ) = 0 Φ x x ′ ′ ( x 0 , a , b , c ) = 0 . \large \left \{ \begin {array} { l } \Phi \left ( { { x _ 0 } , a , b , c } \right ) = 0 \\ { \Phi ’ _ x } \left ( { { x _ 0 } , a , b , c } \right ) = 0 \\ { \Phi ^ { \prime \prime } _ { x x } } \left ( { { x _ 0 } , a , b , c } \right) = 0 \end {array} \right.. ⎩ ⎨ ⎧ Φ ( x 0 , a , b , c ) = 0 Φ ’ x ( x 0 , a , b , c ) = 0 Φ xx ′′ ( x 0 , a , b , c ) = 0 .
در این مثال، f ( x ) = cos x f\left( x \right) = \cos x f ( x ) = cos x
f ’ ( x ) = ( cos x ) ′ = – sin x , f ′ ′ ( x ) = ( – sin x ) ′ = – cos x . \large \begin {align*} f ’ \left ( x \right ) & = \left ( { \cos x } \right ) ^ \prime = – \sin x , \; \; \; \kern-0.3pt \\ f ^ {\prime \prime} \left ( x \right ) & = \left ( { – \sin x } \right ) ^ \prime = – \cos x . \end{align*} f ’ ( x ) f ′′ ( x ) = ( cos x ) ′ = – sin x , = ( – sin x ) ′ = – cos x .
در نتیجه، ضرایب a a a b b b c c c
{ a x 0 2 + b x 0 + c – cos x 0 = 0 2 a x 0 + b + sin x 0 = 0 2 a + cos x 0 = 0 . \large \left\{ \begin {array} { l } a x _ 0 ^ 2 + b { x _ 0 } + c – \cos { x _ 0 } = 0 \\ 2 a { x _ 0 } + b + \sin { x _ 0 } = 0 \\ 2 a + \cos { x _ 0 } = 0 \end {array} \right . . ⎩ ⎨ ⎧ a x 0 2 + b x 0 + c – cos x 0 = 0 2 a x 0 + b + sin x 0 = 0 2 a + cos x 0 = 0 .
با جایگذاری x 0 = 0 {x_0} = 0 x 0 = 0
{ c – 1 = 0 b = 0 2 a + 1 = 0 , ⇒ { a = – 1 2 b = 0 c = 1 . \large { \left\{ \begin {array} { l } c – 1 = 0 \\ b = 0 \\ 2 a + 1 = 0 \end {array} \right . , \; \; } \Rightarrow { \left\{ \begin {array} { l } a = – \frac { 1 } { 2 } \\ b = 0 \\ c = 1 \end{array} \right..} ⎩ ⎨ ⎧ c –1 = 0 b = 0 2 a + 1 = 0 , ⇒ ⎩ ⎨ ⎧ a = – 2 1 b = 0 c = 1 .
بنابراین، سهمی بوسان با تابع کسینوس در نقطه x 0 = 0 x _0 = 0 x 0 = 0
y = – x 2 2 + 1. \large y = – \frac { { { x ^ 2 } } } { 2 } + 1 . y = – 2 x 2 + 1.
همانطور که میبینیم، این معادله متناظر با دو جمله اول بسط مکلورن تابع کسینوس است.
مثال ۳
معادله منحنیِ
y = g ( x ) = a x + b \large y = g \left ( x \right ) = \frac { a } { { x + b } } y = g ( x ) = x + b a
را بیابید که با نمودار تابع لگاریتمی f ( x ) = ln x + 1 f\left( x \right) = \ln x + 1 f ( x ) = ln x + 1 x 0 = 1 x _ 0 = 1 x 0 = 1
حل: دسته منحنی g ( x ) g (x) g ( x ) a a a b b b
{ f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) = g ’ ( x 0 ) . \large \left\{ \begin {array} { l } f \left ( { { x _ 0 } } \right ) = g \left ( { { x _ 0 } } \right ) \\ f ’ \left ( { { x _ 0 } } \right ) = g ’ \left ( { { x _ 0 } } \right ) \end{array} \right . . { f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) = g ’ ( x 0 ) .
مشتقها نیز به صورت زیر محاسبه میشوند:
f ’ ( x ) = ( ln x + 1 ) ′ = 1 x , g ’ ( x ) = ( a x + b ) ′ = – a ( x + b ) 2 \large \begin{align*} f ’ \left ( x \right ) & = \left ( { \ln x + 1 } \right ) ^ \prime = \frac { 1 } { x } , \; \; \; \kern-0.3pt \\ g ’ \left ( x \right ) & = \left ( { \frac { a } { { x + b } } } \right ) ^ \prime = – \frac { a } { { { { \left ( { x + b } \right ) } ^ 2 } } } \end {align*} f ’ ( x ) g ’ ( x ) = ( ln x + 1 ) ′ = x 1 , = ( x + b a ) ′ = – ( x + b ) 2 a
با جایگذاری توابع و مشتقات آنها، معادلههای زیر به دست میآید:
{ ln x 0 + 1 = a x 0 + b 1 x 0 = – a ( x + b ) 2 . \large \left\{ \begin {array} { l } \ln { x _ 0 } + 1 = \frac { a } { { { x _ 0 } + b } } \\ \frac { 1 } { { { x _ 0 } } } = – \frac { a } { { { { \left ( { x + b } \right ) } ^ 2 } } } \end{array} \right.. { ln x 0 + 1 = x 0 + b a x 0 1 = – ( x + b ) 2 a .
برای نقطه x 0 = 1 x _ 0 = 1 x 0 = 1 a a a b b b
{ ln 1 + 1 = a 1 + b 1 1 = – a ( 1 + b ) 2 , ⇒ { a = 1 + b a = – ( 1 + b ) , ⇒ a = – a 2 , ⇒ a + a 2 = 0 , ⇒ a ( 1 + a ) = 0. \large \begin{align*} & \left\{ \begin {array} { l } \ln 1 + 1 = \frac { a } { { 1 + b } } \\ \frac { 1 } { 1 } = – \frac { a } { { { { \left ( { 1 + b } \right ) } ^ 2 } } } \end {array} \right . , \; \; \Rightarrow { \left\{ \begin {array} { l } a = 1 + b \\ a = – \left ( { 1 + b } \right ) \end {array} \right . , \; \; } \\ & \Rightarrow { a = – { a ^ 2 } , \; \; } \Rightarrow { a + { a ^ 2 } = 0 , \; \; } \\ & \Rightarrow { a \left ( { 1 + a } \right ) = 0 . } \end {align*} { ln 1 + 1 = 1 + b a 1 1 = – ( 1 + b ) 2 a , ⇒ { a = 1 + b a = – ( 1 + b ) , ⇒ a = – a 2 , ⇒ a + a 2 = 0 , ⇒ a ( 1 + a ) = 0.
جواب بامعنی معادله اخیر a = − 1 a = -1 a = − 1 b = − 2 b = -2 b = − 2 f ( x ) = ln x + 1 f\left( x \right) = \ln x + 1 f ( x ) = ln x + 1 x 0 = 1 x _ 0 = 1 x 0 = 1
y = g ( x ) = – 1 x – 2 = 1 2 – x . \large y = g \left ( x \right ) = – \frac { 1 } { { x – 2 } } = \frac { 1 } { { 2 – x } } . y = g ( x ) = – x –2 1 = 2– x 1 .
مثال ۴
معادله
y = g ( x ) = a x 3 + b x 2 + c x + d \large y = g \left ( x \right ) = a { x ^ 3 } + b { x ^ 2 } + c x + d y = g ( x ) = a x 3 + b x 2 + c x + d
را به گونهای بنویسید که نمودار آن با منحنی f ( x ) = tan x f\left( x \right) = \tan x f ( x ) = tan x x 0 = 0 x _ 0 = 0 x 0 = 0
حل: در اینجا با دستهای از توابع شامل چهار پارامتر سر و کار داریم. بنابراین، بالاترین مرتبه ممکن تماس منحنیها برابر با 3 3 3 a a a b b b c c c d d d
{ f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) = g ’ ( x 0 ) f ′ ′ ( x 0 ) = g ′ ′ ( x 0 ) f ′ ′ ′ ( x 0 ) = g ′ ′ ′ ( x 0 ) . \large \left\{ \begin {array} { l } f \left ( { { x _ 0 } } \right ) = g \left ( { { x _ 0 } } \right ) \\ f ’ \left ( { { x _ 0 } } \right ) = g ’ \left ( { { x _ 0 } } \right ) \\ f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) = g ^ { \prime \prime } \left ( { { x _ 0 } } \right ) \\ f ^ { \prime \prime \prime } \left ( { { x _ 0 } } \right ) = g ^ { \prime \prime \prime } \left ( { { x _ 0 } } \right ) \end {array} \right.. ⎩ ⎨ ⎧ f ( x 0 ) = g ( x 0 ) f ’ ( x 0 ) = g ’ ( x 0 ) f ′′ ( x 0 ) = g ′′ ( x 0 ) f ′′′ ( x 0 ) = g ′′′ ( x 0 ) .
مشتقات توابع مکعبی به صورت زیر است:
g ’ ( x ) = ( a x 3 + b x 2 + c x + d ) ′ = 3 a x 2 + 2 b x + c , g ′ ′ ( x ) = ( 3 a x 2 + 2 b x + c ) ′ = 6 a x + 2 b , g ′ ′ ′ ( x ) = ( 6 a x + 2 b ) ′ = 6 a . \large \begin{align*} g ’ \left ( x \right ) & = { \left ( { a { x ^ 3 } + b { x ^ 2 } + c x + d } \right ) ^ \prime } = 3 a { x ^ 2 } + 2 b x + c , \\ g ^ { \prime \prime } \left ( x \right ) & = { \left ( { 3 a { x ^ 2 } + 2 b x + c } \right ) ^ \prime } = 6 a x + 2 b , \\ g ^ { \prime \prime \prime } \left ( x \right ) & = { \left ( { 6 a x + 2 b } \right ) ^ \prime } = 6 a . \end {align*} g ’ ( x ) g ′′ ( x ) g ′′′ ( x ) = ( a x 3 + b x 2 + c x + d ) ′ = 3 a x 2 + 2 b x + c , = ( 3 a x 2 + 2 b x + c ) ′ = 6 a x + 2 b , = ( 6 a x + 2 b ) ′ = 6 a .
مشتقات تابع تانژانت نیز برابر است با:
f ’ ( x ) = ( tan x ) ′ = 1 cos 2 x , f ′ ′ ( x ) = ( 1 cos 2 x ) ′ = [ ( cos x ) – 2 ] ′ = – 2 ( cos x ) – 3 ⋅ ( – sin x ) = 2 sin x cos 3 x , f ′ ′ ′ ( x ) = ( 2 sin x cos 3 x ) ′ = ( 2 sin x ) ′ cos 3 x – 2 sin x ( cos 3 x ) ′ cos 6 x = 2 cos 3 x + 6 sin 2 x cos 2 x cos 6 x = 2 + 4 sin 2 x cos 4 x . \large \begin{align*} f ’ \left ( x \right ) & = { \left ( { \tan x } \right ) ^ \prime } = \frac { 1 } { { { { \cos } ^ 2 } x } } , \\ f ^ { \prime \prime } \left ( x \right ) & = { \left ( { \frac { 1 } { { { { \cos } ^ 2 } x } } } \right ) ^ \prime } = { { \left [ { { { \left ( { \cos x } \right ) } ^ { – 2 } } } \right ] ^ \prime } } \\ & = { – 2 { \left ( { \cos x } \right ) ^ { – 3 } } \cdot \left ( { – \sin x } \right ) } = { \frac { { 2 \sin x } } { { { { \cos } ^ 3 } x } } , } \\ f ^ { \prime \prime \prime } \left ( x \right ) & = { \left ( { \frac { { 2 \sin x } } { { { { \cos } ^ 3 } x } } } \right ) ^ \prime } = { \frac { { { { \left ( { 2 \sin x } \right ) } ^ \prime } { { \cos } ^ 3 } x – 2 \sin x { { \left ( { { { \cos } ^ 3 } x } \right ) } ^ \prime } } } { { { { \cos } ^ 6 } x } } } \\ & = { \frac { { 2 \, { { \cos } ^ 3 } x + 6 \, { { \sin } ^ 2 } x \, { { \cos } ^ 2 } x } } { { { { \cos } ^ 6 } x } } } = { \frac { { 2 + 4 \, { { \sin } ^ 2 } x } } { { { { \cos } ^ 4 } x} } . } \end {align*} f ’ ( x ) f ′′ ( x ) f ′′′ ( x ) = ( tan x ) ′ = cos 2 x 1 , = ( cos 2 x 1 ) ′ = [ ( cos x ) –2 ] ′ = –2 ( cos x ) –3 ⋅ ( – sin x ) = cos 3 x 2 sin x , = ( cos 3 x 2 sin x ) ′ = cos 6 x ( 2 sin x ) ′ cos 3 x –2 sin x ( cos 3 x ) ′ = cos 6 x 2 cos 3 x + 6 sin 2 x cos 2 x = cos 4 x 2 + 4 sin 2 x .
در نتیجه، دستگاه معادلات زیر را خواهیم دشت:
{ tan x 0 = a x 0 3 + b x 0 2 + c x 0 + d 1 cos 2 x 0 = 3 a x 0 2 + 2 b x 0 + c 2 sin x 0 cos 3 x 0 = 6 a x 0 + 2 b 2 + 4 sin 2 x 0 cos 4 x 0 = 6 a \large \left\{ \begin {array} { l } \tan { x _ 0 } = a x _ 0 ^ 3 + b x _ 0 ^ 2 + c { x _ 0 } + d \\ \large \frac { 1 } { { { { \cos } ^ 2 } { x _ 0 } } } = 3 a x _ 0 ^ 2 + 2 b { x _ 0 } + c \\ \large \frac { { 2 \sin { x _ 0 } } } { { { { \cos } ^ 3 } { x _ 0 } } } = 6 a { x _ 0 } + 2 b \\ \large \frac { { 2 + 4 { { \sin } ^ 2 } { x _ 0 } } } { { { { \cos } ^ 4 } { x _ 0 } } } = 6 a \end{array} \right. ⎩ ⎨ ⎧ tan x 0 = a x 0 3 + b x 0 2 + c x 0 + d c o s 2 x 0 1 = 3 a x 0 2 + 2 b x 0 + c c o s 3 x 0 2 s i n x 0 = 6 a x 0 + 2 b c o s 4 x 0 2 + 4 s i n 2 x 0 = 6 a
با جایگذاری مقدار x 0 = 0 x _ 0 = 0 x 0 = 0
{ d = 0 c = 1 2 b = 0 6 a = 2 , ⇒ { a = 1 3 b = 0 c = 1 d = 0 . \large { \left\{ \begin {array} { l } d = 0 \\ c = 1 \\ 2 b = 0 \\ 6 a = 2 \end {array} \right . , \; \; } \Rightarrow { \left\{ \begin {array} { l } a = \frac { 1 } { 3 } \\ b = 0 \\ c = 1 \\ d = 0 \end{array} \right..} ⎩ ⎨ ⎧ d = 0 c = 1 2 b = 0 6 a = 2 , ⇒ ⎩ ⎨ ⎧ a = 3 1 b = 0 c = 1 d = 0 .
بنابراین، تابع مکعبی بوسان به صورت زیر است:
y = x 3 3 + x . \large y = \frac { { { x ^ 3 } } } { 3 } + x . y = 3 x 3 + x .
این منحنی، با منحنی تانژانت در مبدأ تماس مرتبه سوم دارد.
توجه کنید که تابع مکعبی حاصل، چندجملهای مکلورن مرتبه سوم تابع تانژانت است.
مثال ۵
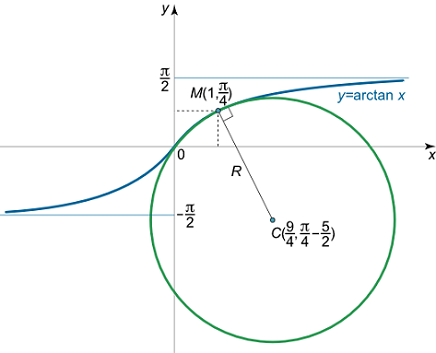
معادله دایره بوسان با منحنی f ( x ) = arctan x f\left( x \right) = \arctan x f ( x ) = arctan x x 0 = 1 x _ 0 = 1 x 0 = 1
حل: واضح است که دو منحنی در نقطه زیر تماس دارند:
( x 0 , y 0 ) = ( 1 , π 4 ) . \large \left ( { { x _ 0 } , { y _ 0 } } \right ) = \left ( { 1 , \frac { \pi } { 4 } } \right ) . ( x 0 , y 0 ) = ( 1 , 4 π ) .
مختصات و مرکز دایره بوسان نیز برابر است با:
a = x 0 – 1 + ( y ’ 0 ) 2 y 0 ′ ′ y ’ 0 , b = y 0 + 1 + ( y ’ 0 ) 2 y 0 ′ ′ , R = [ 1 + ( y ’ 0 ) 2 ] 3 2 ∣ y 0 ′ ′ ∣ . \large { a = { x _ 0 } – \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y ^ { \prime \prime } _ 0 } } } { y ’ _ 0 } , } \; \; \; \kern-0.3pt { b = { y _ 0 } + \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2} } } { { { y ^ { \prime \prime } _ 0 } } } , } \; \; \; \kern-0.3pt { R = \frac { { { { \left [ { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { { y ^ { \prime \prime } _ 0 } } \right | } } . } a = x 0 – y 0 ′′ 1 + ( y ’ 0 ) 2 y ’ 0 , b = y 0 + y 0 ′′ 1 + ( y ’ 0 ) 2 , R = y 0 ′′ [ 1 + ( y ’ 0 ) 2 ] 2 3 .
بنابراین، مشتقها به صورت زیر خواهند بود:
y ’ = ( arctan x ) ′ = 1 1 + x 2 , y ′ ′ = ( 1 1 + x 2 ) ′ = – 2 x ( 1 + x 2 ) 2 . \large { y ’ = { \left ( { \arctan x } \right ) ^ \prime } = \frac { 1 } { { 1 + { x ^ 2 } } } , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) ^ \prime } = – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } . } } y ’ = ( arctan x ) ′ = 1 + x 2 1 , y ′′ = ( 1 + x 2 1 ) ′ = – ( 1 + x 2 ) 2 . 2 x
مقادیر این مشتقها در نقطه x 0 = 1 x _0 = 1 x 0 = 1
y ’ 0 = y ’ ( 1 ) = 1 2 , y 0 ′ ′ = y ′ ′ ( 1 ) = – 1 2 . \large { { y ’ _ 0 } = y ’ \left ( 1 \right ) = \frac { 1 } { 2 } , } \; \; \; \kern-0.3pt { { y ^ { \prime \prime } _ 0 } = y ^ { \prime \prime } \left ( 1 \right ) = – \frac { 1 } { 2 } .} y ’ 0 = y ’ ( 1 ) = 2 1 , y 0 ′′ = y ′′ ( 1 ) = – 2 1 .
مختصات مرکز دایره بوسان نیز به صورت زیر است:
a = x 0 – 1 + ( y ’ 0 ) 2 y 0 ′ ′ y ’ 0 = 1 – 1 + ( 1 2 ) 2 ( – 1 2 ) ⋅ 1 2 = 9 4 = 2.25 ; b = y 0 + 1 + ( y ’ 0 ) 2 y 0 ′ ′ = π 4 + 1 + ( 1 2 ) 2 ( – 1 2 ) = π 4 – 5 2 ≈ – 1.71. \large \begin{align*} a & = { x _ 0 } – \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y ^ { \prime \prime } _ 0 } } } { y ’ _ 0 } = { 1 – \frac { { 1 + { { \left ( { \frac { 1 } { 2 } } \right ) } ^ 2 } } } { { \left ( { – \frac { 1 } { 2 } } \right ) } } \cdot \frac { 1 } { 2 } } = { \frac { 9 } { 4 } = 2. 2 5 ;} \\ b & = { y _ 0 } + \frac { { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } } { { { y ^ { \prime \prime } _ 0 } } } = { \frac { \pi } { 4 } + \frac { { 1 + { { \left ( { \frac { 1 } { 2 } } \right ) } ^ 2 } } } { { \left ( { – \frac { 1 } { 2 } } \right ) } } } = { \frac { \pi } { 4 } – \frac { 5 } { 2 } \approx – 1.71 . } \end {align*} a b = x 0 – y 0 ′′ 1 + ( y ’ 0 ) 2 y ’ 0 = 1– ( – 2 1 ) 1 + ( 2 1 ) 2 ⋅ 2 1 = 4 9 = 2.25 ; = y 0 + y 0 ′′ 1 + ( y ’ 0 ) 2 = 4 π + ( – 2 1 ) 1 + ( 2 1 ) 2 = 4 π – 2 5 ≈ –1.71.
شعاع دایره بوسان نیز برابر است با:
R = [ 1 + ( y ’ 0 ) 2 ] 3 2 ∣ y 0 ′ ′ ∣ = [ 1 + ( 1 2 ) 2 ] 3 2 ∣ – 1 2 ∣ = ( 1 + 1 4 ) 3 2 1 2 = 2 ( 5 4 ) 3 2 = 125 4 ≈ 2.80. \large \begin{align*} R & = \frac { { { { \left [ { 1 + { { \left ( { { y ’ _ 0 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { { y ^ { \prime \prime } _ 0} } \right | } } = { \frac { { { { \left [ { 1 + { { \left ( { \frac { 1 } { 2 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { – \frac { 1 } { 2 } } \right | } } } \\ & = { \frac { { { { \left ( { 1 + \frac { 1 } { 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 1 } { 2 } } } } = { 2 { \left ( { \frac { 5 } { 4 } } \right ) ^ { \large \frac { 3 } { 2 } \normalsize } } } = { \frac { { \sqrt { 1 2 5 } } } { 4 } \approx 2.80.} \end {align*} R = y 0 ′′ [ 1 + ( y ’ 0 ) 2 ] 2 3 = – 2 1 [ 1 + ( 2 1 ) 2 ] 2 3 = 2 1 ( 1 + 4 1 ) 2 3 = 2 ( 4 5 ) 2 3 = 4 125 ≈ 2.80.
بنابراین، مرکز دایره بوسان در نقطه ( 9 4 , π 4 – 5 2 ) \left ( { { \large \frac { 9 } { 4 } \normalsize } , { \large \frac { \pi } { 4 } \normalsize } – { \large \frac { 5 } { 2 } \normalsize } } \right ) ( 4 9 , 4 π – 2 5 )
شکل ۳ اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش منحنی بوسان – به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی منحنی بوسان فیلم آموزشی مثال های یافتن منحنی بوسان