مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع

مساحت مثلث متساوی الساقین برابر «قاعده ضربدر ارتفاع تقسیم بر دو» است. در صورت مشخص بودن اندازه برخی از ضلع‌ها و زاویه‌های این مثلث، امکان استفاده از فرمول هرون و فرمول سینوس برای محاسبه مساحت وجود دارد. در این مقاله از مجله فرادرس، فرمول‌ها و نحوه محاسبه مساحت مثلث متساوی الساقین و انواع مختلف آن را به همراه حل چندین مثال متنوع آموزش می‌دهیم.

مثلث چیست ؟

مثلث، یکی از شکل‌های هندسی پایه است که از سه ضلع تشکیل می‌شود.

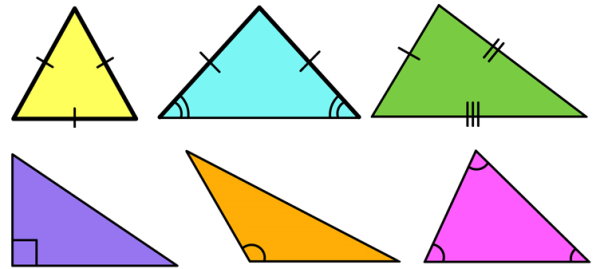
تصویر بالا، انواع مثلث‌ها بر اساس اندازه ضلع‌ها و زاویه‌ها را نمایش می‌دهد:

• انواع مثلث بر اساس اندازه زاویه
  • مثلث حاده
  • مثلث قائم الزاویه
  • مثلث منفرجه
• انواع مثلث بر اساس اندازه ضلع
  • مختلف الاضلاع
  • متساوی الساقین
  • متساوی الاضلاع

مثلث متساوی الساقین چیست ؟

در مطالب قبلی از مجله فرادرس با مثلث متساوی‌الساقین آشنا شدیم. مثلث متساوی الساقین، یکی از انواع مثلث با دو ضلع و دو زاویه برابر است.

در این مثلث، ضلع‌های برابر با عنوان «ساق» و ضلع سوم با عنوان «قاعده» شناخته می‌شود.

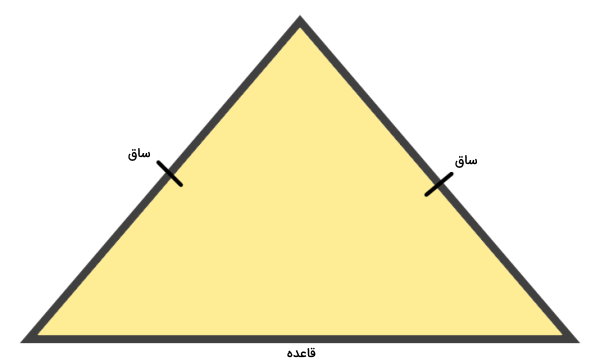
مساحت مثلث متساوی الساقین چگونه بدست می آید ؟

مساحت مثلث متساوی الساقین، سطح محدود به ضلع‌های آن است که معمولا توسط فرمول «قاعده ضرب در ارتفاع تقسیم بر 2» محاسبه می‌شود:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

مثال 1: محاسبه مساحت مثلث متساوی الساقین

قاعده و ارتفاع مثلث متساوی الساقین، به ترتیب برابر 10 و 14 سانتی‌متر است. مساحت این مثلث را حساب کنید.

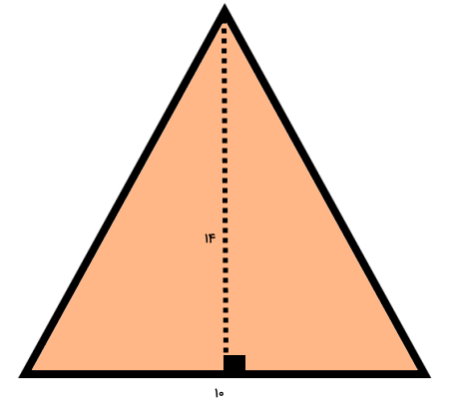
خط‌چین نمایش داده شده در تصویر بالا، ارتفاع نظیر قاعده مثلث است. رابطه مساحت مثلث‌های متساوی الساقین بر اساس ارتفاع و قاعده به صورت زیر نوشته می‌شود:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث متساوی الساقین

• قاعده برابر 10 سانتی‌متر
• ارتفاع برابر 14 سانتی‌متر

اندازه‌های معلوم را درون رابطه بالا قرار می‌دهیم و آن را حل می‌کنیم:

۲ ÷ (14 $$\times$$ 10) = مساحت مثلث متساوی الساقین

۲ ÷ (140) = مساحت مثلث متساوی الساقین

70 = مساحت مثلث متساوی الساقین

مساحت مثلث برابر 70 سانتی‌متر مربع است. البته، فرمول‌های بیشتری برای محاسبه مساحت انواع مثلث‌های متساوی الساقین در حالت‌های مختلف وجود دارد. در بخش بعدی، ابتدا به معرفی فرمول‌های عمومی و سپس فرمول‌های اختصاصی مساحت مثلث متساوی الساقین به همراه حل چند مثال می‌پردازیم.

فرمول های مساحت مثلث متساوی الساقین چه هستند ؟

شناخته شده‌ترین فرمول مساحت مثلث، «قاعده ضرب در ارتفاع تقسیم بر دو» است که عبارت جبری آن به صورت زیر نوشته می‌شود:

$$
A = \frac {b \times h } { 2 }
$$

• A: مساحت مثلث
• b: قاعده مثلث
• h: ارتفاع مثلث

هر مثلث دارای سه ارتفاع و سه قاعده است. در صورت مشخص بودن اندازه این ارتفاع‌ها و قاعده‌ها، امکان تعیین مساحت فراهم می‌شود.

مثال 2: محاسبه مساحت مثلث متساوی الساقین با ارتفاع و قاعده

مساحت مثلث متساوی الساقین با ارتفاع 6 و قاعده 7 را به دست بیاورید.

به دلیل مشخص بودن اندازه قاعده و ارتفاع، فرمول مساحت مثلث به صورت زیر نوشته می‌شود:

$$
A = \frac {b \times h } { 2 }
$$

• A: مساحت مثلث
• b: قاعده مثلث برابر 7
• h: ارتفاع مثلث برابر 6

اندازه‌های معلوم را درون فرمول بالا قرار می‌هیم:

$$
A = \frac {6 \times 7 } { 2 }
$$

$$
A = \frac {42 } { 2 }
$$

$$
A = 21
$$

در نتیجه، مساحت مثلث متساوی الساقین برابر 21 است.

فرمول مساحت مثلث متساوی الساقین با سه ضلع

یکی دیگر از روش‌های کلی برای محاسبه مساحت مثلث متساوی الساقین، استفاده از فرمول هرون است. در صورت معلوم بودن اندازه سه ضلع مثلث، مساحت آن توسط فرمول زیر محاسبه می‌شود:

$$
A=\sqrt{s(s-a)(s-b)(s-c)}
$$

• A: مساحت
• s: نصف محیط مثلث
• a: اندازه ضلع اول
• b: اندازه ضلع دوم
• c: اندازه ضلع سوم

مثال 3: محاسبه مساحت مثلث متساوی الساقین با سه ضلع

مساحت مثلث نمایش داده شده در تصویر زیر را محاسبه کنید.

در تصویر بالا، اندازه هر سه ضلع مثلث داده شده است. از این‌رو، برای محاسبه مساحت مثلث می‌توانیم از فرمول مساحت مثلث با سه ضلع معلوم استفاده کنیم. مطابق با این فرمول داریم:

$$
A=\sqrt{s(s-a)(s-b)(s-c)}
$$

• A: مساحت
• s: نصف محیط مثلث
• a: اندازه ضلع اول برابر 5
• b: اندازه ضلع دوم برابر 5
• c: اندازه ضلع سوم برابر 8

نصف محیط مثلث به صورت زیر محاسبه می‌شود:

$$
s= \frac {5+5+8} {2}
$$

$$
s= \frac {18} {2}
$$

$$
s= 9
$$

مقدار بالا را به همراه اندازه ضلع‌ها، درون فرمول هرون قرار می‌دهیم و آن را حل می‌کنیم:

$$
A=\sqrt{9(9-5)(9-5)(9-5)}
$$

$$
A=\sqrt{9(4)(4)(1)}
$$

$$
A=\sqrt{144}
$$

$$
A=12
$$

مساحت مثلث متساوی الساقین برابر 12 است.

فرمول مساحت مثلث متساوی الساقین با سینوس

در برخی از موارد، اندازه تمام ضلع‌های مثلث یا اندازه یکی از ضلع‌ها و قاعده نظیر آن مشخص نیست. در این شرایط، اگر دو ضلع و زاویه بین آن‌ها معلوم باشد، مساحت مثلث از فرمول زیر به دست می‌آید:

$$
Area=\frac{1}{2} b c \sin A
$$

• Area: مساحت
• b: اندازه یکی از ضلع‌ها
• c: اندازه ضلع دیگر
• A: زاویه بین دو ضلع با اندازه معلوم

مثال 4: محاسبه مساحت مثلث متساوی الساقین با دو ضلع و زاویه بین

مساحت مثلث زیر چند است؟

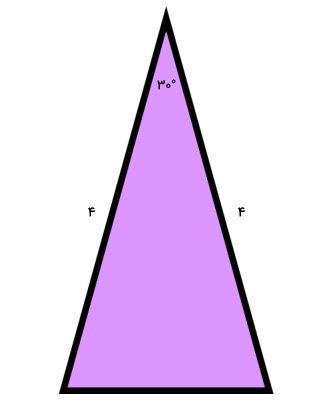
در مثلث بالا، اندازه دو ضلع و زاویه بین آن‌ها داده شده است. به همین دلیل، فرمول مساحت مثلث با سینوس را می‌نویسیم:

$$
Area=\frac{1}{2} b c \sin A
$$

• Area: مساحت
• b: اندازه یکی از ضلع‌ها برابر 4
• c: اندازه ضلع دیگر برابر 4
• A: زاویه بین دو ضلع با اندازه معلوم برابر 30 درجه

$$
Area=\frac{1}{2} \times 4 \times 4 \times \sin 30^{\circ}
$$

سینوس زاویه 30 درجه برابر 0/5 است. این مقدار را در رابطه بالا قرار داده و حل مسئله را ادامه می‌دهیم:

$$
Area=2 \times 4 \times 0.5
$$

$$
Area=8 \times 0.5
$$

$$
Area=4
$$

مساحت مثلث متساوی الساقین برابر با 4 است.

 

فرمول‌های بیشتری برای محاسبه مساحت مثلث با سینوس وجود دارند. در صورت علاقه به آشنایی با این فرمول‌ها، مطالعه مطلب «محاسبه مساحت مثلث با سینوس» را به شما پیشنهاد می‌کنیم.

فرمول مساحت مثلث متساوی الساقین بدون ارتفاع

یکی از روش‌های خاص محاسبه مساحت مثلث متساوی الساقین، استفاده از اندازه ساق یا قاعده است. اگر زاویه بین دو ساق مثلث متساوی الساقین برابر با 90 باشد، یک شکل خاص با عنوان «مثلث متساوی الساقین قائم الزاویه» به وجود می‌آید.

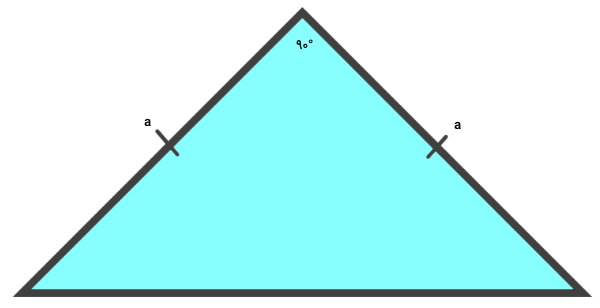
به دلیل قائم الزاویه بودن مثلث متساوی الساقین بالا، امکان استفاده از قضیه فیثاغورس در آن وجود دارد. با کمک این فرمول، اگر اندازه ساق مثلث متساوی الساقین قائم الزاویه مشخص باشد، مساحت آن به صورت زیر نوشته می‌شود:

$$
A=\frac{ a^ {2} }{2}
$$

• A: مساحت
• a: اندازه ساق

به همین ترتیب، در صورت مشخص بودن اندازه وتر (قاعده)، مساحت مثلث متساوی الساقین قائم الزاویه از فرمول زیر به دست می‌آید:

$$
A=\frac{ c^ {2} }{4}
$$

• A: مساحت
• c: اندازه وتر

مثال 5: محاسبه مساحت مثلث متساوی الساقین قائم الزاویه

مساحت مثلث زیر را تعیین کنید.

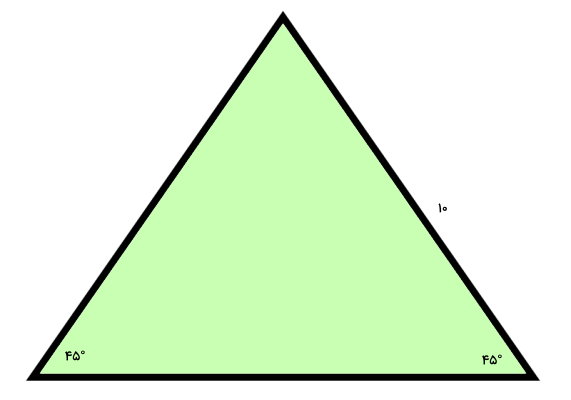
برابر بودن دو زاویه مثلث، متساوی الساقین بودن مثلث بالا را نمایش می‌دهد. جمع زوایای داخلی مثلث برابر 180 درجه است. به این ترتیب، زاویه نامعلوم مثلث متساوی الساقین بالا برابر خواهد بود با:

$$
180^{\circ} - 45^ {\circ}- 45^ {\circ} = 90^ {\circ}
$$

زاویه سوم مثلث برابر 90 درجه است. بنابراین، این مثلث به عنوان یک مثلث متساوی الساقین قائم الزاویه در نظر گرفته می‌شود. از این‌رو، با استفاده از فرمول زیر می‌توا مساحت مثلث را تعیین کرد:

$$
A=\frac{ a^ {2} }{2}
$$

• A: مساحت مثلث متساوی الساقین قائم الزاویه
• a: اندازه ساق

$$
A=\frac{ 10^ {2} }{2}
$$

$$
A=\frac{ 100 }{2}
$$

$$
A=50
$$

مساحت مثلث برابر 50 است. فرمول مورد استفاده برای حل این مثال، فرم دیگری از فرمول مساحت مثلث قائم الزاویه است. در صورت علاقه به یادگیری روش‌های محاسبه مساحت مثلث قائم الزاویه، مطالعه مطلب «مساحت مثلث قائم الزاویه — حل تمرین و مثال‌های متنوع» را به شما پیشنهاد می‌کنیم.

مثال های مساحت مثلث متساوی الساقین

در این بخش، چند مثال متنوع از مسائل مساحت مثلث‌های متساوی الساقین را حل می‌کنیم.

مثال 6: محاسبه ارتفاع مثلث متساوی الساقین

مساحت مثلث زیر برابر 48 سانتی‌متر مربع است. ارتفاع نظیر قاعده را حساب کنید.

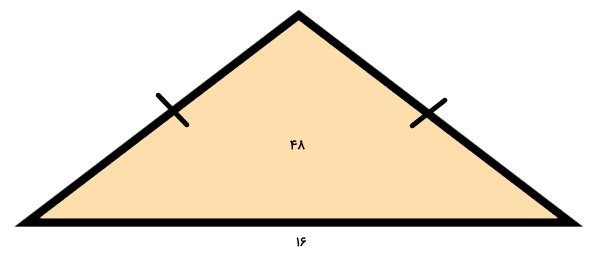
مطابق با تصویر بالا، مثلث مورد سوال از نوع متساوی الساقین است. با این وجود، این ویژگی، تاثیری بر روی محاسبه ارتفاع نظیر قاعده ندارد، چراکه برای تعیین ارتفاع هر نوع مثلث با استفاده از مساحت، باید فرمول زیر را بنویسیم:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$
A = \frac {b \times h } { 2 }
$$

• A: مساحت مثلث برابر 48
• b: قاعده مثلث برابر 16
• h: ارتفاع مثلث

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم و آن را حل می‌کنیم:

$$
48 = \frac {16 \times b } { 2 }
$$

$$
48 \times 2= 16 \times b
$$

$$
96= 16 \times b
$$

$$
\frac{96} {16}= b
$$

$$
6= b
$$

ارتفاع نظیر قاعده مثلث متساوی الساقین برابر 6 است.

مثال 7: محاسبه مساحت مثلث متساوی الساقین با وتر

مساحت یک مثلث متساوی الساقین قائم الزاویه با وتر 7 را حساب کنید.

فرمول مساحت مثلث متساوی الساقین قائم الزاویه بر اساس وتر به صورت زیر نوشته می‌شود:

$$
A=\frac{ c^ {2} }{4}
$$

• A: مساحت
• c: اندازه وتر برابر 7

$$
A=\frac{ 7^ {2} }{4}
$$

$$
A=\frac{ 49 }{4}
$$

$$
A=12.25
$$

مساحت مثلث برابر 12/25 است.

مثال 8: مساحت قسمت رنگی مثلث

ارتفاع نظیر قاعده یک مثلث متساوی را رسم کرده‌ایم. مساحت قسمت رنگی را به دو روش محاسبه کنید.

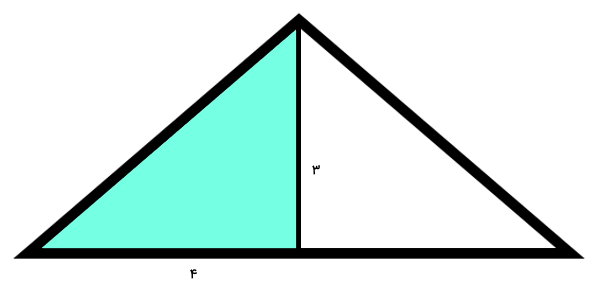
روش اول

در مثلث‌های متساوی الساقین، ارتفاع، قاعده را به دو بخش مساوی تقسیم می‌کند. به عبارت دیگر، در تصویر بالا، قاعده مثلث برابر 8 و مساحت بخش رنگی، نصف مساحت مثلث کامل است. مساحت مثلث کامل از رابطه زیر به دست می‌آید:

$$
A = \frac {b \times h } { 2 }
$$

• A: مساحت مثلث
• b: قاعده مثلث برابر 8 (دو برابر 4)
• h: ارتفاع مثلث 3

$$
A = \frac {8 \times 3 } { 2 }
$$

$$
A = \frac {24} { 2 }
$$

$$
A = 12
$$

مساحت مثلث کامل برابر 12 است. بنابراین، مساحت بخش رنگی مثلث برابر با 6 خواهد بود.

روش دوم

ارتفاع، بر روی قاعده عمود می‌شود. از این‌رو، بخش رنگی، یک مثلث قائم الزاویه با دو ساق به اندازه‌های 3 و 4 است. در مثلث‌های قائم الزاویه، مساحت مثلث از ضرب دو ساق تقسیم بر دو به دست می‌آید:

$$
\frac {3 \times 4} {2}
$$

$$
\frac {12} {2}
$$

$$
6
$$

در نتیجه، مساحت بخش رنگی مثلث متساوی الساقین برابر 6 است.

محاسبه آنلاین مساحت مثلث متساوی الساقین

یکی دیگر از روش‌های محاسبه سریع و آسان مساحت مثلث‌های متساوی الساقین، استفاده از سایت‌های اینترنتی نظیر سایت Calculator.net (+)، سایت Triangle calculator (+)، سایت ncalculators (+) و موتور جستجوی گوگل است. از بین این موارد، سایت Calculator.net، ابزارهای پیشرفته‌تری دارد.

ساده‌ترین راه برای محاسبه آنلاین مساحت مثلث، استفاده از موتور جستجوی گوگل است. به این منظور، باید عبارت‌هایی نظیر «مثلث متساوی الساقین» یا «Isosceles triangle» را جستجو کرد. به این ترتیب، کادری مقابل تصویر زیر در بالای صفحه نتایج ظاهر می‌شود.

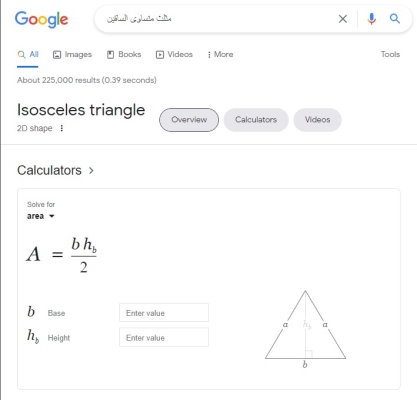
با وارد کردن اندازه قاعده مثلث در کادر مقابل عنوان «b Base» و ارتفاع مثلث در کادر مقابل عنوان «h_b Height»، مساحت مثلث محاسبه می‌شود و به نمایش در می‌آید.

مثال 9: محاسبه مساحت مثلث با گوگل

مساحت یک مثلث متساوی الساقین با ارتفاع 13 و قاعده 7 را توسط موتور جستجوی گوگل حساب کنید.

به منظور محاسبه مساحت مثلث، ابتدا با جستجوی عبارت‌های مربوطه، به صفحه نمایش ماشین حساب گوگل می‌رویم. سپس، عدد 7 را در کادر مقابل عنوان b و عدد 13 را در مقابل کادر h_b وارد می‌کنیم.

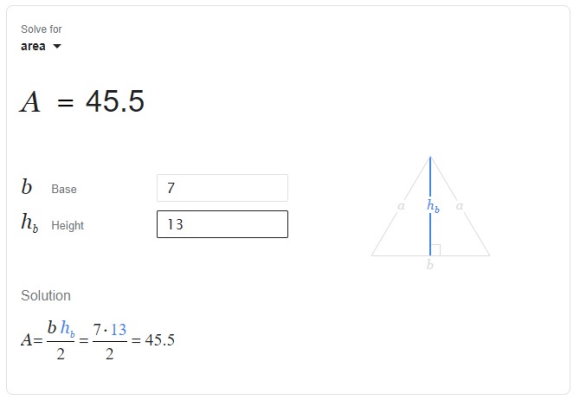
در نتیجه، مساحت مثلث برابر 45/5 است.

سوالات متداول در رابطه با مثلث متساوی الساقین و مساحت آن

در این مطلب از مجله فرادرس با مثلث متساوی‌الساقین و چگونگی محاسبه مساحت آن آشنا شدیم. در این بخش، به برخی از سوالات پرتکرار در رابطه با مثلث‌های متساوی الساقین و نحوه محاسبه مساحت آن‌ها پاسخ می‌دهیم.

تعریف مثلث متساوی الساقین چیست ؟

مثلث متساوی الساقین، مثلثی با دو ضلع (ساق) برابر است.

مساحت مثلث متساوی الساقین چگونه محاسبه می‌شود ؟

مساحت مثلث‌های متساوی الساقین با ضرب قاعده در ارتفاع تقسیم بر دو محاسبه می‌شود. البته فرمول‌های مثلثاتی و فرمول هرون نیز در انجام این محاسبات کاربرد دارند.

فرمول مساحت مثلث متساوی الساقین بدون ارتفاع چیست ؟

فرمول هرون (فرمول مساحت مثلث با سه ضلع)، به عنوان فرمول مساحت مثلث بدون ارتفاع شناخته می‌شود.

مساحت مثلث متساوی الساقین قائم الزاویه چگونه بدست می آید ؟

مساحت مثلث متساوی الساقین قائم الزاویه برابر مجذور ساق بر عدد 2 یا تقسیم مجذور وتر بر عدد 4 است.