مساحت استوانه و محاسبه آن | به زبان ساده

در مطالب قبلی مجله فرادرس، با روش محاسبه مساحت برخی از اشکال و احجام هندسی از قبیل مثلث، دایره، مربع، مستطیل، کره، متوازی‌الاضلاع، و ذوزنقه آشنا شدیم. در این آموزش، فرمول محاسبه مساحت استوانه را همراه با حل چند مثال بیان خواهیم کرد.

استوانه چیست؟

اگر به شکل یک قوطی نوشابه دقت کرده باشید، می‌بینید که شبیه یک استوانه است. «استوانه» (Cylinder) یک حجم است که دو دایره موازی و هم‌اندازه در بالا و پایین دارد. این دایره‌ها را «قاعده» (Base) می‌نامیم. فاصله بین دو قاعده را نیز «ارتفاع» (Height) می‌گوییم و معمولاً با $$h$$ نشان می‌دهیم. اگر قاعده‌های بالا و پایین استوانه در یک راستا باشند، استوانه را قائم و اگر بر هم منطبق نباشند، استوانه را مایل می‌نامیم. شکل زیر استوانه مایل و قائم را نشان می‌دهد.

فرمول مساحت استوانه قائم چیست؟

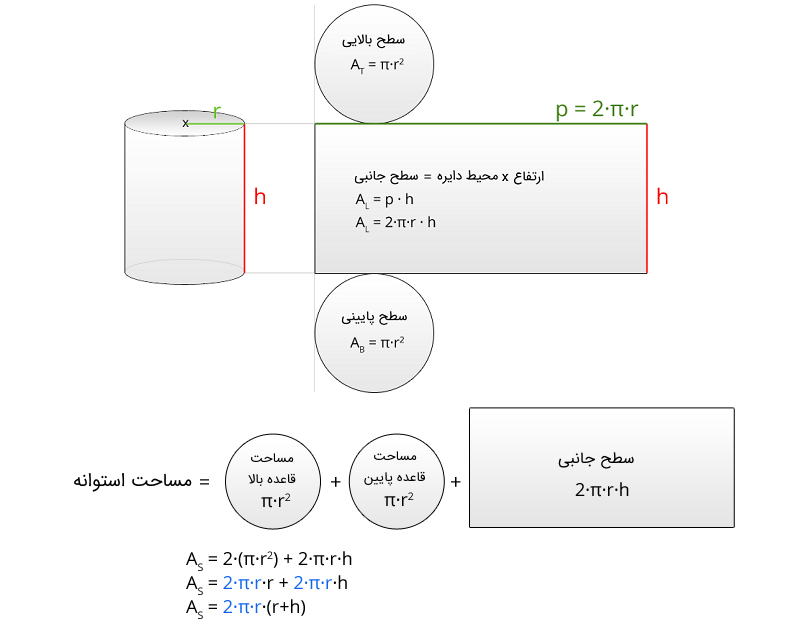
منظور از مساحت استوانه، در واقع مساحت سطح آن است. برای درک بهتر اندازه سطح احجام هندسی، بهترین کار این است که اصطلاحاً آن‌ها را باز کنیم. استوانه سه وجه دارد: یک وجه جانبی و دو وجه بالا و پایین که دایره هستند. اگر استوانه را باز کنیم، می‌توانیم به راحتی فرمولی برای محاسبه مساحت آن ارائه کنیم. شکل زیر استوانه‌ای را نشان می‌دهد که ارتفاع آن برابر با $$h$$ و شعاع قاعده آن $$r$$ است. در این شکل، سطوح باز شده استوانه نیز نشان داده شده‌اند. همان‌طور که می‌بینیم، برای محاسبه مساحت استوانه باید مساحت دو دایره بالا و پایین مربوط به قاعده‌ها و مساحت مستطیل را که مربوط به سطح جانبی استوانه است، با هم جمع کنیم.

بنابراین، مساحت استوانه‌ای که ارتفاع آن برابر با $$h$$ و شعاع قاعده آن $$r$$ است، برابر خواهد بود با:

$$ \large \boxed{ A = 2 \pi r ^ 2 + 2 \pi r h = 2 \pi r (h + r )} $$

تصویر متحرک زیر مفهوم مساحت استوانه و فرمول آن را به خوبی نشان می‌دهد.

آموزش نگارش – پایه هفتم

شروع یادگیری

آموزش ریاضی – پایه هشتم

شروع یادگیری

آموزش محاسبات سریع ریاضی

شروع یادگیری

آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی

شروع یادگیری

آموزش هندسه پایه دهم – هندسه ۱

شروع یادگیری

آموزش عربی – پایه نهم

شروع یادگیری

آموزش ریاضیات گسسته – پایه دوازدهم

شروع یادگیری

آموزش ریاضی – پایه نهم

شروع یادگیری

آموزش ریاضی پایه هفتم

شروع یادگیری

آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

شروع یادگیری

برای آشنایی بیشتر با محاسبه مساحت اشکال مختلف هندسی، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

مساحت استوانه مایل چگونه به دست می‌آید؟

مساحت استوانه مایل نیز دقیقاً با همان فرمول محاسبه مساحت استوانه قائم به دست می‌آید؛ یعنی اگر استوانه‌ مایلی با ارتفاع $$h$$ و شعاع قاعده $$r$$ داشته باشیم، مساحت آن برابر خواهد بود با:

$$ \large \boxed{ A = 2 \pi r ^ 2 + 2 \pi r h = 2 \pi r (h + r )} $$

مثال های محاسبه مساحت استوانه

در این بخش، چند مثال از محاسبه مساحت استوانه را حل می‌کنیم.

مثال اول مساحت استوانه

یک قوطی استوانه‌ای شکل داریم که شعاع قاعده آن برابر با ۴ سانتی‌متر و ارتفاعش ۱۳ سانتی‌متر است. مساحت سطح قوطی چقدر است؟ (فرض کنید قوطی یک استوانه کامل است)

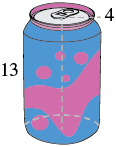
حل: با توجه به اینکه شعاع $$r=4\,\text{cm}$$ و ارتفاع $$h=13\, \text{cm}$$ است، از فرمول بالا استفاده می‌کنیم ($$\pi$$ را برابر با $$3.14$$ در نظر می‌گیریم):

$$ \large \begin {align*}
S & = 2 \pi { r } ^ { 2} +2 \pi r h \\
& = 2 \left ( 3 . 1 4 \right ) { 4 } ^ { 2 } + 2 \left ( 3 . 1 4 \right ) \left ( 4 \right ) 1 3 \\ & = 427.04 \;\text{cm}^2
\end {align*} $$

مثال دوم مساحت استوانه

یک پیتزا به شکل استوانه داریم که ارتفاع آن برابر با $$a=2 \, \text{cm}$$ و شعاع قاعده‌اش برابر با $$z=15\, \text{cm}$$ است.

حل: مساحت سطح پیتزا برابر است با:

$$ \large \begin {align*}
S & = 2 \pi { z } ^ { 2} +2 \pi z a \\
& = 2 \left ( 3 . 1 4 \right ) { 15} ^ { 2 } + 2 \left ( 3 . 1 4 \right ) \left ( 15 \right ) 2 \\ & = 1601.4 \;\text{cm}^2
\end {align*} $$

مثال سوم مساحت استوانه

استوانه مایل زیر با ارتفاع و شعاع قاعده مشخص داده شده است. مساحت سطح این استوانه را محاسبه کنید.

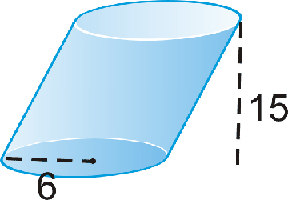
حل: با توجه به شکل، ارتفاع $$ h = 15$$ و شعاع قاعده $$ r = 6 $$ را داریم. بنابراین، مساحت آن به صورت زیر محاسبه می‌شود:

$$ \large \begin {align*}
S & = 2 \pi { r } ^ { 2} +2 \pi r h \\
& = 2 \left ( 3 . 1 4 \right ) { 6 } ^ { 2 } + 2 \left ( 3 . 1 4 \right ) \left ( 6 \right ) 15 \\ & = 791.28
\end {align*} $$

مثال چهارم مساحت استوانه

مساحت سطح استوانه‌ای برابر با ۴۰۰ سانتی‌متر مربع است. اگر شعاع قاعده آن ۵ سانتی‌متر باشد، ارتفاع استوانه چقدر است؟

حل: از فرمول مساحت استوانه استفاده می‌کنیم:

$$ \large
\begin {align*} A & = 2 \pi r ^ 2 + 2 \pi r h
\\ 400 & =2 (3.14)( 5)^2 + 2 (3.14) (5)h
\\ 400 & = 157+31.4 (h)
\\ & \Rightarrow 243 = 31.4 h \Rightarrow h = 7.74 \, \text{cm}
\end {align*}$$

برای یادگیری اشکال مختلف هندسی و محاسبه محیط، مساحت و حجم آن‌ها، توصیه می‌کنیم آموزش‌های مجله فرادرس که در این زمینه تهیه شده‌اند را مطالعه کنید:

• چهار ضلعی ها در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• چندضلعی و تعریف آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• آشنایی با چند وجهی ها — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• دایره، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مثلث، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مربع و محاسبه محیط و مساحت آن — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مستطیل و محاسبات آن — به زبان ساده (+ فیلم آموزش رایگان)
• متوازی‌الاضلاع، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش رایگان)
• لوزی و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• کایت یا شبه‌لوزی، تعریف و محاسبات آن در هندسه — به زبان ساده
• ذوزنقه چیست؟ | محاسبات و فرمول‌ها به زبان ساده (+فیلم آموزش رایگان)
• بیضی، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مخروط، کره و استوانه — حجم و مساحت اشکال هندسی به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مخروط و محاسبان آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• استوانه و مفاهیم آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• آشنایی با منشور و محاسبات آن — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مکعب‌، منشور مربعی و مکعب‌مستطیل — به زبان ساده (+ دانلود فیلم آموزش رایگان)
• مکعب در هندسه — به زبان ساده (+ دانلود فیلم آموزش رایگان)
• مساحت دایره — به زبان ساده (+ فیلم آموزش رایگان)
• مساحت مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• مساحت مستطیل — به زبان ساده (+ فیلم آموزش رایگان)
• مساحت لوزی — به زبان ساده (+ فیلم آموزش رایگان)
• محاسبه مساحت ذوزنقه — به زبان ساده
• مساحت کره و محاسبه آن | به زبان ساده
• مساحت مکعب مستطیل و محاسبه آن | به زبان ساده
• مساحت استوانه و محاسبه آن | به زبان ساده
• محیط دایره — به زبان ساده (+ فیلم آموزش رایگان)
• محیط مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• محیط مستطیل و محاسبه آن — به زبان ساده (+ فیلم آموزش رایگان)
• محیط لوزی — به زبان ساده (+ فیلم آموزش رایگان)
• محیط بیضی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• حجم کره و محاسبه آن | به زبان ساده
• حجم مخروط و محاسبه آن | به زبان ساده