مجموع یابی دنباله ها — به زبان ساده
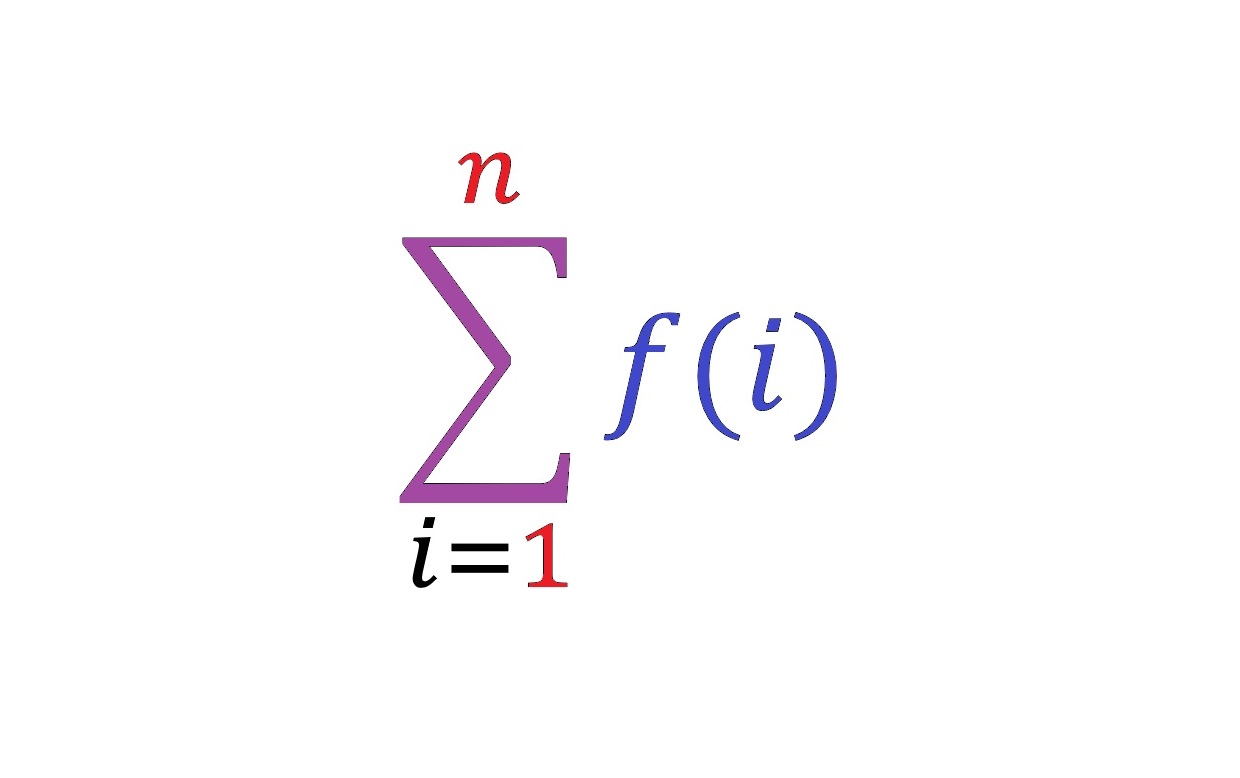
در آموزشهای قبلی مجله فرادرس با دنبالهها آشنا شدیم. در این آموزش نمادها و قضایای مربوط به جمع جملات یک دنباله را ارائه خواهیم کرد که اصطلاحاً مجموع یابی (Summation) نامیده میشود. در ادامه ابتدا یک تعریف را بیان میکنیم و سپس موارد دیگر را بر اساس آن شرح خواهیم داد.
نماد مجموع یابی
تعریف: دنباله $$\left\{ a_{n} \right\}_{n=k}^{\infty}$$ و اعداد $$ m $$ و $$ p $$ را در نظر بگیرید که در نامساوی $$k \leq m \leq p$$ صدق میکنند. مجموع از $$ m $$ تا $$ p $$ دنباله $$\left\{a_{n}\right\}$$ به صورت زیر نوشته میشود:
$$ \large \sum _ { n = m } ^ { p } a _ { n } = a _ { m } + a _ { m + 1 } + \ldots + a _ { p } $$
متغیر $$ n$$ شاخص یا اندیس مجموع یابی نامیده میشود. عدد $$ m $$ کران پایین مجموع یابی و $$p$$ کران بالای مجموع یابی است.
تعریف بالا به سادگی یک نماد کوتاه را برای جمع کردن جملات دنباله $$\left\{ a_{n} \right\}_{n=k}^{\infty} $$ از $$ a _ m $$ تا $$ a _ p $$ نشان میدهد. نماد $$\Sigma $$ حرف یونانی بزرگ سیگما و کوتاه شده sum به معنی مجموع است. کرانهای بالا و پایین مجموع یابی بیان میکنند که با کدام جمله شروع کنیم و با کدام جمله به پایان برسیم. برای مثال، برای دنباله $$a_{n} = 2n-1 $$ با $$ n \ge 1 $$، میتوانیم مجموع $$ (a _ 3 + a _ 4 + a _ 5 + a _ 6) $$ را به صورت زیر بنویسیم:
$$ \large \begin {array} { r c l } \displaystyle { \sum _ { n = 3 } ^ { 6 } ( 2 n - 1 ) } & = & ( 2 ( 3 ) - 1 ) + ( 2 ( 4 ) - 1 ) + ( 2 ( 5 ) - 1 ) + ( 2 ( 6 ) - 1 ) \\ & = & 5 + 7 + 9 + 11 \\ & = & 32 \\ \end {array} $$
متغیر شاخص یک متغیر ساختگی است که میتوان آن را با هر حرف دیگری نشان داد، بدون اینکه بر مقدار مجموع تأثیری داشته باشد. به عبارت دیگر، میتوان نوشت:
$$ \large \displaystyle { \sum _ { n = 3 } ^ { 6 } ( 2 n - 1 ) } = \displaystyle { \sum _ { k = 3 } ^ { 6 } ( 2 k - 1 ) } = \displaystyle { \sum _ { j = 3 } ^ { 6 } ( 2 j - 1 ) } $$
یکی از مواردی که میتوانیم از نماد مجموع یابی استفاده کنیم، در تعاریف ریاضیاتی است. برای مثال، نماد مجموع یابی به ما این توانایی را میدهد که چندجملهایها را به صورت توابعی به فرم زیر بیان کنیم:
$$ \large f ( x ) = \displaystyle { \sum _ { k = 0 } ^ { n } a _ { k } x ^ { k } } $$
که در آن، $$ a _ k $$ اعدادی حقیقی برای $$ k = 0 , 1 , ... , n $$ هستند. علامت مجموع یابی در عملیات ماتریسی نیز بسیار مفید است. برای مثال، میتوانیم ضرب $$i$$اُمین سطر $$ R_ i $$ ماتریس $$A = [a_{ij}]_{m \times n}$$ و ستون $$j$$اُم $$ C_ j $$ ماتریس $$B = [b_{ij}]_{n \times r} $$ را به شکل زیر بنویسیم:
$$ \large R i \cdot C j = \displaystyle { \sum _ { k = 1 } ^ { n } a _ { i k } b _ { k j } } $$
مثال اول مجموع یابی دنباله ها
مجموعهای زیر را بیابید.
- (الف) $$ \displaystyle { \sum _ { k = 1 } ^ { 4 } \dfrac { 1 3 } { 1 0 0 ^ k } } $$
- (ب) $$ \displaystyle { \sum _ { n = 0 } ^ { 4 } \dfrac { n ! } { 2 } } $$
- (ج) $$ \displaystyle { \sum _ { n = 1 } ^ { 5 } \dfrac { ( - 1 ) ^ { n + 1 } } { n } ( x - 1 ) ^ n } $$
حل (الف): $$ k = 1 $$ را در فرمول $$\frac{13}{100^k} $$ جایگذاری کرده و جملات را تا $$ k = 4 $$ با هم جمع میکنیم:
$$ \large \begin {array} { r c l } \displaystyle { \sum _ { k = 1 } ^ { 4 } \dfrac { 1 3 } { 1 0 0 ^ k } } & = & \dfrac { 1 3 } { 1 0 0 ^ 1 } + \dfrac { 1 3 } { 1 0 0 ^ 2 } + \dfrac { 1 3 } { 1 0 0 ^ 3 } + \dfrac { 1 3 } { 1 0 0 ^ 4 } \\ & = & 0 . 1 3 + 0 . 0 0 1 3 + 0 . 0 0 0 0 1 3 + 0 . 0 0 0 0 0 0 1 3 \\ & = & 0 . 1 3 1 3 1 3 1 3 \\ \end {array} $$
حل (ب): مشابه مورد قبل، مقدار $$ n $$ را برابر با مقادیر $$0 $$ تا $$ 4 $$ قرار میدهیم و خواهیم داشت:
$$ \large \begin {array} { r c l } \displaystyle { \displaystyle { \sum _ { n = 0 } ^ { 4 } \dfrac { n ! } { 2 } } } & = & \dfrac { 0 ! } { 2 } + \dfrac { 1 ! } { 2 } + \dfrac { 2 ! } { 2 } + \dfrac { 3 ! } { 2 } = \dfrac { 4 ! } { 2 } \\ & = & \dfrac { 1 } { 2 } + \dfrac { 1 } { 2 } + \dfrac { 2 \cdot 1 } { 2 } + \dfrac { 3 \cdot 2 \cdot 1 } { 2 } + \dfrac { 4 \cdot 3 \cdot 2 \cdot 1 } { 2 } \\ & = & \dfrac { 1 } { 2 } + \dfrac { 1 } { 2 } + 1 + 3 + 1 2 \\ & = & 17 \\ \end {array} $$
حل (ج): مقدار $$ n $$ را از $$ 1 $$ تا $$ 5 $$ قرار میدهیم و داریم:
$$ \large \begin {array} { r c l } \displaystyle { \sum _ { n = 1 } ^ { 5 } \dfrac { ( - 1 ) ^ { n + 1 } } { n } ( x - 1 ) ^ n } & = & \dfrac { ( - 1 ) ^ { 1 + 1 } } { 1 } ( x - 1 ) ^ 1 + \dfrac { ( - 1 ) ^ { 2 + 1 } } { 2 } ( x - 1 ) ^ 2 + \dfrac { ( - 1 ) ^ { 3 + 1 } } { 3 } ( x - 1 ) ^ 3 \\ & & + \dfrac { ( - 1 ) ^ { 1 + 4 } } { 4 } ( x - 1 ) ^ 4 + \dfrac { ( - 1 ) ^ { 1 + 5 } } { 5 } ( x - 1 ) ^ 5 \\ & = & ( x - 1 ) - \dfrac { ( x - 1 ) ^ 2 } { 2 } + \dfrac { ( x - 1 ) ^ 3 } { 3 } - \dfrac { ( x - 1 ) ^ 4 } { 4 } + \dfrac { ( x - 1 ) ^ 5 } { 5 } \\ \end {array} $$
مثال دوم مجموع یابی دنباله ها
عبارات زیر را با استفاده از نماد مجموع بنویسید.
- (الف) $$ 1 + 3 + 5 + \ldots + 117 $$
- (ب) $$ 1 - \dfrac { 1 } { 2 } + \dfrac { 1 } { 3 } - \dfrac { 1 } { 4 } + - \ldots + \dfrac { 1 } { 1 1 7 } $$
- (ج) $$ 0 . 9 + 0 . 0 9 + 0 . 0 0 9 + \ldots + 0 . \underbrace { 0 \cdots 0 } _ { \text {(n-1 )}} 9 $$
حل (الف): جملات مجموع یک دنباله حسابی را تشکیل میدهند که جمله اول آن $$ a = 1 $$ و قدر نسبت $$ d = 2 $$ است. فرمول $$ n $$ جمله این دنباله $$a_{n} = 1 + (n-1)2 = 2n-1$$ برای $$ n \ge 1 $$ است. در این مرحله، فرمول $$ 2 n - 1 $$ را برای جملات داریم که کران پایین مجموع $$ n = 1 $$ است. برای حل کامل مسئله، لازم است کران بالای مجموع را نیز تعیین کنیم. به عبارت دیگر، لازم است مشخص کنیم که کدام مقدار $$n$$ منجر به جمله $$ 117 $$ میشود. با قرار دادن $$ a _ n = 117 $$ مقدار $$2n-1=117 $$ یا $$ n = 59 $$ را خواهیم داشت. پاسخ نهایی به صورت زیر است:
$$ \large \begin {array} { r c l } 1 + 3 + 5 + \ldots + 1 1 7 & = & \displaystyle { \sum _ { n = 1 } ^ { 5 9 } ( 2 n - 1 ) } \end {array} $$
حل (ب): همه جملات را به صورت کسر و علامتهای جمع را منها را به صورت جمع مینویسیم. در نتیجه، خواهیم داشت:
$$ \large \dfrac { 1 } { 1 } + \dfrac { - 1 } { 2 } + \dfrac { 1 } { 3 } + \dfrac { - 1 } { 4 } + \ldots + \dfrac { 1 } { 1 1 7 } $$
صورت کسرها $$ -1 $$ و $$ 1 $$ است که به صورت یکی در میان تکرار میشود. در واقع میتوانیم اینها را یک سری هندسی با جمله اول $$ a = 1 $$ و قدر نسبت $$ r = - 1 $$ در نظر بگیریم که به صورت $$c_{n} = (-1)^{n-1} $$ برای $$ n \ge 1 $$ نوشته میشود. مخرجها نیز یک دنباله حسابی را نشان میدهند که جمله اول آن $$ a = 1 $$ و قدر نسبت آن $$ d = 1 $$ است، یعنی $$ d _ n = n $$ برای $$ n \ge 1 $$. بنابراین، فرمول $$a_{n} = \frac{(-1)^{n-1}}{n} $$ را برای جملات خواهیم داشت و کرانهای پایین و بالای مجموع، به ترتیب، $$ n = 1 $$ و $$ n = 117 $$ خواهند بود. در نتیجه، میتوان نوشت:
$$ \large \begin {array} { r c l } 1 - \dfrac { 1 } { 2 } + \dfrac { 1 } { 3 } - \dfrac { 1 } { 4 } + - \ldots + \dfrac { 1 } { 1 1 7 } & = & \displaystyle { \sum _ { n = 1 } ^ { 1 1 7 } \dfrac { ( - 1 ) ^ { n - 1 } } { n } } \end {array} $$
حل (ج): فرمول $$n$$اُمین جمله این دنباله $$a_{n} = \frac{9}{10^{n}} $$ برای $$ n \ge 1 $$ است. بنابراین، فرمولی برای مجموع با کران پایین خواهیم داشت. برای به دست آوردن کران بالای مجموع میدانیم که باید $$ n - 1 $$ صفر سمت راست اعشار قبل از عدد $$ 9 $$ تولید کنیم و به مخرج $$ 10 ^ n $$ نیاز داریم. بنابراین، $$ n$$ کران بالای مجموع خواهد بود. از آنجا که $$ n $$ در کرانها مورد استفاده قرار میگیرد، لازم است یک حرف دیگر برای شاخص مجموع تعیین کنیم. بدین منظور $$ k $$ را انتخاب میکنیم:
$$ \large \begin {array} { r c l } 0 . 9 + 0 . 0 9 + 0 . 0 0 9 + \ldots + 0 . \underbrace { 0 \cdots 0 } _ { \text {(n-1)}} 9 & = & \displaystyle { \sum _ { k = 1 } ^ { n } \dfrac { 9 } { 1 0 ^ {k } } } \end {array} $$
قضیه زیر برخی از ویژگیهای عمومی نماد مجموع یابی را بیان میکند. گرچه این ویژگیها شاید کمتر در جبر مورد استفاده قرار گیرند، اما در حسابان نقش ویژهای دارند.
خواص نماد مجموع یابی
قضیه: فرض کنید $$\left\{a_{n}\right\} $$ و $$\left\{b_{n}\right\} $$ دنبالههایی باشند که در مجموعهای زیر تعریف شدهاند. در این صورت، خواهیم داشت:
- $$ \displaystyle { \sum _ { n = m } ^ { p } \left ( a _ { n } \pm b _ { n } \right ) = \sum _ { n = m } ^ { p } a _ { n } \pm \sum _ { n = m } ^ { p } b _ { n } } $$
- $$ \displaystyle { \sum _ { n = m } ^ { p } c \, a _ { n } = c \sum _ { n = m } ^ { p } a _ { n } } $$ برای هر عدد حقیقی $$c$$
- $$ \displaystyle { \sum _ { n = m } ^ { p } a _ { n } = \sum _ { n = m } ^ { j } a _ { n } + \sum _ { n = j + 1 } ^ { p } a _ { n } } $$ برای هر عدد طبیعی $$m \leq j < j+1 \leq p $$
- $$ \displaystyle { \sum _ { n = m } ^ { p } a _ { n } = \sum _ { n = m + r } ^ { p + r } a _ { n - r } } $$ برای هر عدد $$ r $$
تصاعد حسابی و تصاعد هندسی
اکنون وقت آن است که چند مجموع تصاعد حسابی و هندسی را بررسی کنیم. تصاعد حسابی $$a_{k} = a + (k-1) d $$ برای $$ k \ge 1 $$ را در نظر بگیرید.
مجموع $$ n $$ جمله اول را $$ S $$ مینامیم. برای به دست آوردن فرمولی برای $$ S $$، آن را به شکلهای زیر میتوان نوشت:
$$ \large \begin{array} {ccccccccccc} S & = a + ( a + d ) + \ldots + ( a + ( n - 2 ) d ) + ( a + ( n - 1 ) d ) \\ S & = ( a + ( n - 1 ) d ) + ( a + ( n - 2 ) d ) + \ldots + ( a + d ) + a \\ \end {array} $$
اگر این دو معادله را با هم جمع کنیم و جملات متناظر را با هم ترکیب کنیم، خواهیم داشت:
$$ \large 2 S = ( 2 a + ( n - 1 ) d ) + ( 2 a + ( n - 1 ) d ) + \ldots + ( 2 a + ( n - 1 ) d ) + ( 2 a + ( n - 1 ) d ) $$
سمت راست این معادله شامل $$ n $$ جمله است که همه آنها برابر با $$(2a + (n-1)d) $$ هستند. بنابراین، تساوی $$2S = n(2a + (n-1)d) $$ را خواهیم داشت. با تقسیم دو طرف معادله بر ۲، فرمول زیر به دست میآید:
$$ \large S = \dfrac { n } { 2 } ( 2 a + ( n - 1 ) d ) $$
اگر مقدار $$2a + (n-1)d $$ را به صورت $$ a + ( a + ( n - 1 ) d ) = a _ 1 + a _ { n } $$ بنویسیم، آنگاه فرمول زیر را خواهیم داشت:
$$ \large S = n \left ( \dfrac { a _ 1 + a _ { n } } { 2 } \right) $$
یک راه مفید برای به خاطر سپردن این فرمول، تشخیص این موضوع است که مجموع را به صورت ضرب $$ n$$ و میانگین اولین و $$ n $$اُمین جمله نوشتهایم.
برای به دست آوردن فرمول مجموع هندسی، تصاعد هندسی $$a_{k} = ar^{k-1} $$ را برای $$ k \ge 1 $$ در نظر میگیریم و $$ S $$ را مجدداً به عنوان مجموع $$ n $$ جمله اول مشخص میکنیم. با مقایسه $$ S $$ و $$ r S $$، داریم:
$$ \large \begin {align*} S & = a + a r + a r ^ 2 + \ldots + a r ^ { n - 2 } + a r ^ { n - 1 } \\ r S & = a r + a r ^ 2 + \ldots + a r ^ { n - 2 } + a r ^ { n - 1 } + a r ^ { n } \end {align*} $$
با کم کردن معادله دوم از معادله اول همه جملات جز $$ a $$ و $$ a r ^ n $$ حذف میشوند و به رابطه $$S - rS = a - ar^{n} $$ خواهیم رسید. با فاکتورگیری معادله $$S(1-r) = a \left(1-r^{n}\right) $$ را خواهیم داشت. با در نظر گرفتن $$r \neq 1 $$، میتوانیم دو طرف را بر $$(1-r) $$ تقسیم کنیم:
$$ \large S = a \left ( \dfrac { 1 - r ^ n } { 1 - r } \right ) $$
اگر $$ a $$ را در صورت توزیع کنیم، $$ a - a r ^ { n } = a _ 1 - a _ { n + 1 } $$ منجر به فرمول زیر میشود:
$$ \large S = \dfrac { a _ 1 - a _ { n + 1 } } { 1 - r } $$
در حالتی که $$ r= 1 $$ است، فرمول زیر را داریم:
$$ \large S = \underbrace { a + a + \ldots + a } _ {n} = n a $$
این نتایج را میتوان به صورت زیر خلاصه کرد:
- مجموع $$ n $$ جمله اول تصاعد حسابی $$a_{k}= a + (k-1)d $$ برای $$ k \ge 1 $$ به صورت زیر است:
$$ \large S = \displaystyle { \sum _ { k = 1 } ^ { n } a _ { k } } = n \left ( \dfrac { a_ { 1 } + a _ { n } } { 2 } \right ) = \dfrac { n } { 2 } ( 2 a + ( n - 1 ) d ) $$
- مجموع $$ n $$ جمله نخست تصاعد هندسی $$a_{k}= ar^{k-1} $$ برای $$k\ge 1 $$ برابر با یکی از دو مورد زیر است:
- $$ S = \displaystyle { \sum _ { k = 1 } ^ { n } a _ { k } } = \dfrac { a _ { 1 } - a _ { n + 1 } } { 1 - r } = a \left ( \dfrac { 1 - r ^ n } { 1 - r } \right ) $$، اگر $$r \neq 1 $$ باشد.
- $$ S = \displaystyle { \sum _ { k = 1 } ^ { n } a _ { k } = \sum _ { k = 1 } ^ { n } a = n a } $$، اگر $$ r = 1 $$ باشد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- آموزش ریاضیات عمومی 1
- آموزش چرتکه — به زبان ساده
- حسابان کسری — به زبان ساده
- اکسترمم محلی تابع — از صفر تا صد
^^











خیلی خوب توضیح دادید من کلاس هشتم هستم اما به مبحث سیگما، انتگرالو… علاقه زیادی داریم. راجب تخفیف هم بگم لطفا این تخفیف 20000 تومانی را همیشگی کنید خیلی به درد میخوره ممنونم??
سلا محمد عزیز.
خوشحالیم که آموزشهای مجله فرادرس برایتان مفید بوده است.
سالم و سربلند باشید.