فیلتر بالا گذر اکتیو — از صفر تا صد
یک فیلتر بالا گذر اکتیو (Active High Pass Filter) یا HPF را میتوان با استفاده از ترکیب یک فیلتر شبکه RC بالا گذر پسیو با یک تقویتکننده عملیاتی ایجاد کرد. در این صورت یک فیلتر بالا گذر با خاصیت تقویتکنندگی ایجاد میشود. در این مطلب قصد داریم با اصول کار یک فیلتر بالا گذر اکتیو آشنا شویم.
عملکرد اساسی یک فیلتر بالا گذر اکتیو بسیار مشابه با نوع معادل آن یعنی مدار RC فیلتر بالا گذر پسیو است، البته این دو فیلتر با یکدیگر در این نکته متفاوت هستند که فیلتر بالا گذر اکتیو از یک تقویتکننده عملیاتی یا اپ امپ در طراحی خود استفاده میکند که همین المان موجب ایجاد تقویتکنندگی و بهره کنترل برای مدار فیلتر میشود.
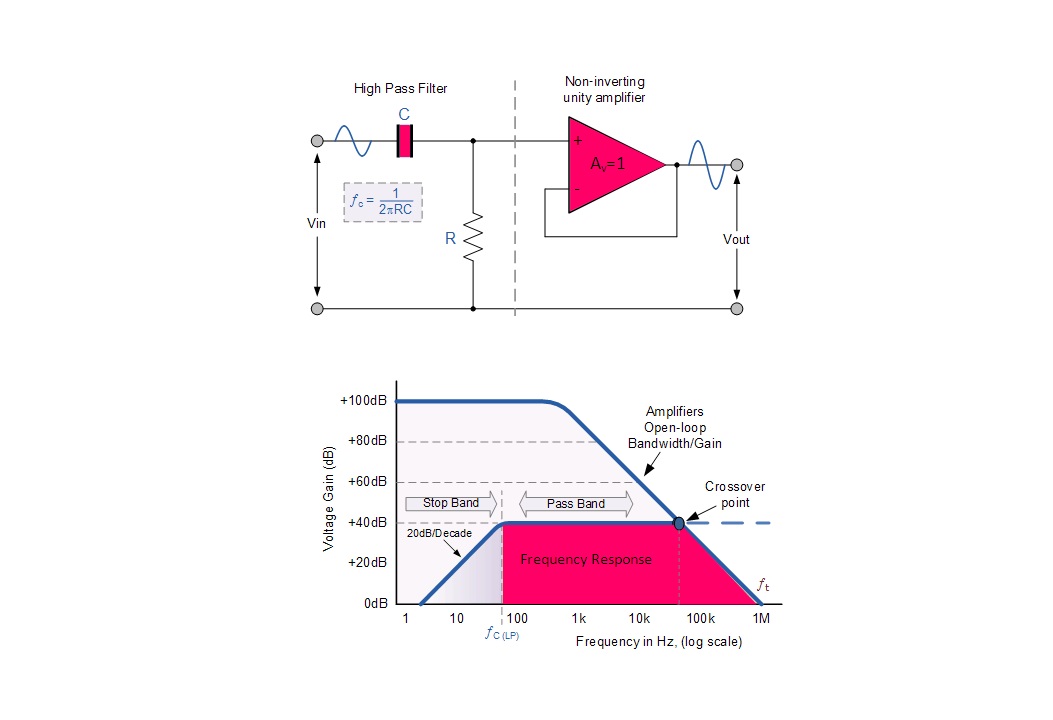
مانند مدار فیلتر پایین گذر اکتیو که در مطالب قبلی مجله فرادرس به بررسی آنها پرداختیم، سادهترین فرم یک فیلتر بالا گذر اکتیو این است که یک تقویتکننده عملیاتی معکوس کننده یا غیر معکوس کننده را به یک مدار فیلتر شبکه RC بالا گذر پسیو متصل کنیم. در تصویر زیر نمایی از یک مدار فیلتر بالا گذر اکتیو مرتبه اول نشان داده شده است.
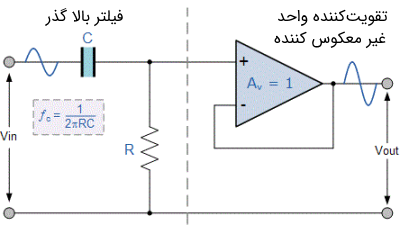
بر خلاف فیلترهای بالا گذر پسیو که دارای پاسخ فرکانسی بینهایت هستند، پاسخ فرکانسی باند عبور بیشینه یک فیلتر بالا گذر اکتیو توسط مشخصههای حلقه باز و یا پهنای باند تقویتکننده عملیاتی مورد استفاده محدود میشود. در واقع این عوامل یک فیلتر بالا گذر اکتیو را به صورت یک فیلتر میان گذر با فرکانس قطع بالا نشان میدهند که فرکانس قطع از طریق انتخاب اپ امپ و بهره آن تعیین میشود.
در مطلب تقویتکنندههای عملیاتی به این موضوع اشاره کردیم که پاسخ فرکانسی بیشینه یک اپ امپ با توجه به حاصل ضرب بهره اپ امپ در پهنای باند آن تعیین میشود. ولتاژ حلقه باز یا $$ A _ V $$ یک تقویتکننده عملیاتی مورد استفاده، محدودیت پهنای باند را مشخص میکند. در حالی که پاسخ حلقه بسته اپ امپ با پاسخ حلقه باز متقاطع است.
تقویتکنندههای عملیاتی متداول مورد استفاده مانند uA741، دارای بهره ولتاژ DC حلقه باز (بدون هیچ نوع فیدبک) بیشینه در حدود ۱۰۰ دسی بل هستند که این مقدار با افزایش فرکانس ورودی، با سرعت رول آف $$ -20dB/Decade $$ یا $$ -6db/Octave $$ کاهش مییابد. بهره اپ امپ uA741 تا زمانی که به بهره واحد یا صفر دسی بل و یا فرکانس گذار اپ امپ $$ f _ t $$ (که در حدود ۱ مگا هرتز است) برسد، همچنان کاهش پیدا میکند.
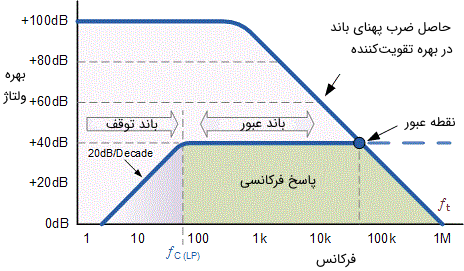
همین امر باعث میشود که تقویتکننده عملیاتی دارای منحنی پاسخ فرکانسی بسیار شبیه به یک فیلتر پایین گذر مرتبه اول داشته باشد. نمایی ازمنحنی پاسخ فرکانسی یک تقویتکننده عملیاتی معمولی در تصویر زیر نشان داده شده است.
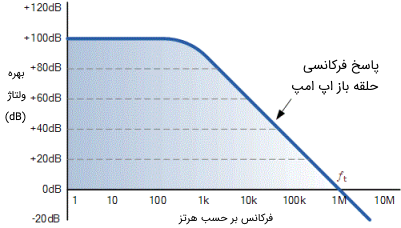
بنابراین عملکرد یک فیلتر بالا گذر در فرکانسهای بالا توسط فرکانس گذر از بهره واحد، محدود شده است. میتوان گفت که این فرکانس، پهنای باند کلی تقویتکننده حلقه باز را مشخص میکند. مقدار حاصل ضرب بهره در پهنای باند یک تقویتکننده عملیاتی برای تقویتکنندههای سیگنالهای کوچک از حدود ۱۰۰ کیلو هرتز شروع میشود و تا حدود ۱ گیگا هرتز برای تقویتکنندههای ویدئویی دیجیتالی پرسرعت میرسد. فیلترهای اکتیو مبتنی بر تقویتکنندههای عملیاتی میتوانند به دقت و عملکرد بسیار خوبی دست یابند، به شرط اینکه مقاومتها و خازنهای با تلرانس بسیار پایین استفاده شود.
تحت شرایط کاری نرمال، باند عبور بیشینهای که برای یک فیلتر اکتیو بالا گذر حلقه بسته و یا یک فیلتر میان گذر مورد نیاز است، پایینتر از فرکانس گذار حلقه باز بیشینه قرار دارد. اما در هنگام طراحی مدار یک فیلتر اکتیو، انتخاب یک اپ امپ مناسب برای مدار امری بسیار ضروری است؛ زیرا هرگونه از دست رفتن سیگنالهای فرکانس بالا ممکن است باعث اعوجاج سیگنال شود.
فیلتر بالا گذر اکتیو مرتبه یک
یک فیلتر بالا گذر اکتیو مرتبه اول یا تک قطبی، همان طور که از نام آن مشخص است، فرکانسهای پایین را تضعیف و از بین میبرد و فقط سیگنالهای فرکانس بالا را از خود عبور میدهد. این مدار ساختمان سادهای دارد و از یک بخش فیلتر پسیو همراه با یک تقویتکننده عملیاتی غیر معکوس کننده تشکیل شده است.
پاسخ فرکانسی مدار مشابه با پاسخ فرکانسی یک فیلتر پسیو است و تنها تفاوت این دو نمودار در این است که با افزایش بهره تقویتکننده، دامنه سیگنال افزایش مییابد و برای یک تقویتکننده غیر معکوس کننده، مقدار بهره ولتاژ باند عبور بر اساس رابطه $$ 1 + R _ 2 / R _ 1 $$ محاسبه میشود. مشاهده میکنیم که این همان رابطهای است که برای مدار یک فیلتر پایین گذر مورد استفاده قرار میگیرد.
فیلتر بالا گذر اکتیو با تقویتکنندگی
در تصویر زیر، مدار یک فیلتر بالا گذر اکتیو با خاصیت تقویتکنندگی (Amplification) نشان داده شده است.
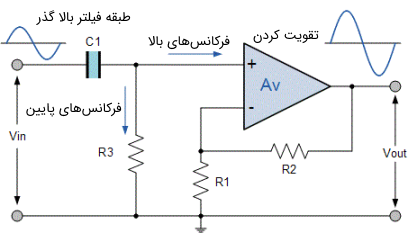
فیلتر بالا گذر مرتبه اول، از یک فیلتر پسیو همراه با یک تقویتکننده غیر معکوس کننده تشکیل شده است. پاسخ فرکانسی مدار مشابه با پاسخ فرکانسی یک فیلتر پسیو است و فقط در این نکته متفاوت هستند که دامنه سیگنال متناظر با بهره تقویتکننده افزایش مییابد. برای مدار یک تقویتکننده غیر معکوس کننده، دامنه بهره ولتاژ برای فیلتر به صورت تابعی از مقاومت فیدبک $$ R _ 2 $$ تقسیم بر مقاومت ورودی $$ R _ 1 $$ و به صورت زیر محاسبه میشود:
$$ \text {voltage gain, (AV)} = \frac { V _ { o u t }} { V _ { i n }} = \frac { A _ F ( \frac { f } { f _ c} ) } { \sqrt{ 1 + ( \frac { f } { f _ c} ) ^ 2 } } $$
در رابطه بالا، $$ A _ F $$ بهره باند عبور فیلتر است که با رابطه $$ 1 + R _ 2 / R _ 1 $$ محاسبه میشود. همچنین $$ f $$ برابر با فرکانس سیگنال ورودی بر حسب هرتز و $$ f _ c $$ فرکانس قطع بر حسب هرتز است.
همانند فیلتر پایین گذر، عملکرد یک فیلتر بالا گذر اکتیو را نیز میتوان از روی معادله بهره ولتاژ به دست آمده به صورت زیر تشخیص داد:
- در فرکانسهای بسیار پایین $$ f < f _ c $$، بهره ولتاژ به صورت $$ \frac { V _ { o u t } } { V _ { i n } } < A _ F $$ است.
- در فرکانس قطع $$ f = f _ c $$، بهره ولتاژ برابر با $$ \frac { V _ { o u t } } { V _ { i n } } = \frac { A _ F } { \sqrt { 2 } } = 0.707 A _ F $$ است.
- در فرکانسهای بسیار بزرگ $$ f > f _ c $$، معادله بهره ولتاژ با نامساوی $$ \frac { V _ { o u t } } { V _ { i n } } \cong A _ F $$ برابر میشود.
بنابراین میتوان گفت که یک فیلتر بالا گذر اکتیو دارای بهره $$ A _ F $$ است که از مقدار صفر هرتز در فرکانسهای پایین شروع میشود و با افزایش فرکانس به مقدار نقطه قطع فرکانس پایین $$ f _ c $$ در $$ 20dB/decade $$ میرسد. در فرکانس $$ f _ c $$ بهره برابر با $$ 0. 7 0 7 * A _ F $$ است و پس از فرکانس $$ f _ c $$، تمام فرکانسها، جزو فرکانسهای باند عبور محسوب میشوند، بنابراین فیلتر دارای بهره ثابت $$ A _ F $$ با بزرگترین فرکانس است که توسط پهنای باند حلقه بسته اپ امپ مشخص میشود.
در مدارات فیلترها، دامنه بهره باند عبور مدار معمولا بر حسب دسیبل یا dB بیان میشود و تابعی از بهره ولتاژ فیلتر است. در نتیجه دامنه بهره ولتاژ به صورت زیر محاسبه میشود:
$$ A _ V (dB ) = 20 log _ {10 } ( { \frac { V _ { o u t } } { V _ { i n } } ) } $$
$$ \therefore -3 dB = 20 log _ { 10 } ( 0.707 { \frac { V _ { o u t } } { V _ { i n } } ) } $$
برای یک فیلتر مرتبه اول، منحنی پاسخ فرکانسی فیلتر با سرعت $$ 20 dB / decade $$ یا $$ 6 dB / octave $$ تا نقطه فرکانس قطع معین بالا میرود که همیشه $$ - 3 dB $$ زیر مقدار بهره بیشینه قرار دارد. همانند فیلترهای دیگری که در مطالب قبلی مجله فراردرس بررسی شد، فرکانس گوشه یا قطع پایین $$ f _ c $$ را نیز میتوان با فرمول زیر به دست آورد:
$$ f _ c = \frac { 1 } { 2 \pi R C} HZ $$
نحوه محاسبه زاویه فاز یا شیفت فاز سیگنال خروجی از فیلتر بالا گذر اکتیو کاملا با فرمولهای شیفت فاز متعلق به فیلتر RC پسیو مشابه است و در حالت کلی میتوان گفت که با سیگنال ورودی پیش فاز (leads) است. این مقدار در فرکانس قطع $$ f _ c $$ برابر با 45+ درجه است و به صورت زیر محاسبه میشود:
$$ \text { phase shift} \; \phi = \tan ^ { -1 } ( \frac { 1 } { 2 \pi f R C } ) $$
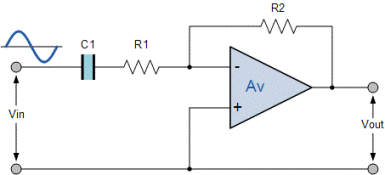
یک فیلتر بالا گذر اکتیو مرتبه اول ساده، را میتوان با پیکربندی یک تقویتکننده عملیاتی معکوس کننده نیز ایجاد کرد. در تصویر زیر نمونهای از یک مدار فیلتر بالا گذر اکتیو مرتبه اول با تقویتکننده عملیاتی معکوس کننده نشان داده شده است.
همچنین منحنی پاسخ فرکانسی این فیلتر مطابق با تصویر زیر است.
مثال 1: فیلتر بالا گذر اکتیو
یک فیلتر بالا گذر اکتیو مرتبه اول، دارای بهره باند عبور برابر با ۲ و فرکانس قطع پایین گوشه برابر با ۱ کیلو هرتز است. اگر خازن ورودی مقدار ۱۰ نانو فاراد داشته باشد، مقدار مقاومت تعیین کننده فرکانس قطع و مقاومتهای بهره در شبکه فیدبک را به دست آورید. همچنین منحنی پاسخ فرکانسی محتمل برای فیلتر را ترسیم کنید.
حل:
با توجه به مقدار فرکانس قطع گوشه برابر با ۱ کیلو هرتز و نیز مقدار خازن ۱۰ نانو فاراد، مقدار مقاومت R به صورت زیر به دست میآید:
$$ R = \frac { 1 } { 2 \pi f _ c C } = \frac { 1 } { 2 \pi * 1000 * 10 * 10 ^ { - 9 } } = 15 . 92K \Omega $$
نزدیکترین مقدار به این مقاومت، برابر با ۱۶ کیلو اهم است. بر اساس صورت سوال، بهره باند عبور این فیلتر بالا گذر اکتیو یا $$ A _ F $$ برابر با ۲ است. این مقدار بر اساس فرمول زیر محاسبه میشود:
$$ A _ F = 1 + \frac { R _ 2 } { R _ 1 } $$
$$ 2 = 1 + \frac { R _ 2 } { R _ 1 } $$
$$ \frac { R _ 2 } { R _ 1 } = 1 $$
چون مقدار مقاومت $$ R _ 2 $$ تقسیم بر مقاومت $$ R _ 1 $$ برابر با عدد یک به دست آمده است، در نتیجه مقاومت $$ R _ 1 $$ باید برابر با مقدار مقاومت $$ R _ 2 $$ باشد تا بهره باند عبور در فیلتر $$ A _ F $$ برابر با مقدار ۲ باشد. حال میتوانیم برای دو مقاومت فیدبک، یک مقدار برابر، مثلا 10 کیلو اهم انتخاب کنیم.
بنابراین برای یک فیلتر بالا گذر با فرکانس قطع گوشه برابر با ۱ کیلو هرتز، مقادیر مقاومت R و خازن C به ترتیب برابر با ۱۰ کیلو اهم و ۱۰ نانو فاراد خواهد بود. مقدار دو مقاومت فیدبک برای ایجاد بهره باند عبور برابر با ۲، به صورت $$ R _ 1 = R _ 2 = 10 \; K \Omega $$ محاسبه میشوند.
اطلاعات مورد نیاز برای ترسیم نمودار «منحنی پاسخ فرکانسی بود» (Bode) این فیلتر را میتوان با جایگذاری مقادیر به دست آمده از بالا در یک بازه فرکانسی از ۱۰۰ هرتز تا ۱۰۰ کیلو هرتز در معادله بهره ولتاژ ترسیم کرد:
$$ \text {voltage gain, (AV)} = \frac { V _ { o u t }} { V _ { i n }} = \frac { A _ F ( \frac { f } { f _ c} ) } {\sqrt{ 1 + ( \frac { f } { f _ c} ) ^ 2 } } $$
با استفاده از معادله فوق، مقادیر جدول زیر به دست میآیند:
| بهره بر حسب دسیبل ($$ 20 log _ {10 } \frac { V _ { o u t } } { V _ { i n } }$$) | بهره ولتاژ ($$ \frac { V _ { o u t } } { V _ { i n}} $$) | فرکانس $$ f $$ (هرتز) |
| 14.02- | 0.2 | 100 |
| 8.13- | 0.39 | 200 |
| 0.97- | 0.89 | 500 |
| 1.93 | 1.25 | 800 |
| 3.01 | 1.41 | 1000 |
| 5.56 | 1.9 | 3000 |
| 5.85 | 1.96 | 5000 |
| 5.98 | 1.99 | 10000 |
| 6.02 | 2 | 50000 |
| 6.02 | 2 | 100000 |
حال دادههای پاسخ فرکانسی در جدول فوق را میتوانیم در نمودار زیر ترسیم کنیم. در باند توقف فیلتر (از ۱۰۰ هرتز تا ۱ کیلو هرتز)، بهره با سرعت $$ 20 dB / decade $$ افزایش مییابد. اما در باند عبور و پس از فرکانس قطع فیلتر، یعنی در فرکانسهای بعد از $$ f _ c = 1 \; k H z $$، بهره در مقدار ۶٫۰۲ دسی بل ثابت باقی میماند. محدوده فرکانس بالای باند عبور فیلتر بالا گذر، توسط پهنای باند حلقه باز اپ امپ استفاده شده در مدار فیلتر تعیین میشود که قبلا راجع به این موضوع بحث کردیم. بنابراین نمودار بود فیلتر بالا گذر اکتیو به صورت زیر به دست میآید.
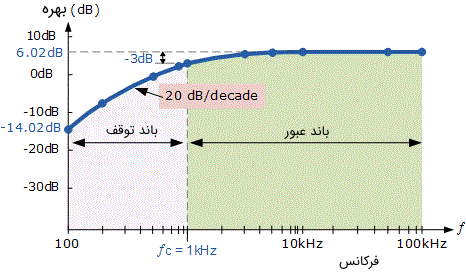
یک فیلتر بالا گذر اکتیو، در مدارات متنوعی از جمله تقویتکنندههای صوتی، سیستمهای بلندگو و یا «اکوالایزر» (Equalizers) کاربرد دارد. فیلتر بالا گذر در این مدارات برای رساندن سیگنالهای فرکانس بالا به «بلندگوهای پربسامد کوچکتر» (Tweeter Speakers) و یا کاهش هر نویز فرکانس پایین و یا «اعوجاجات نوع پر سر و صدا» (Rumble Type Distortion) مورد استفاده قرار میگیرد. زمانی که یک فیلتر بالا گذر اکتیو در کاربردهای صوتی به کار گرفته شود، به آن «فیلتر ارتقای صدای زیر» (Treble Boost Filter) میگویند.
فیلتر بالا گذر اکتیو مرتبه دو
همانند فیلترهای نوع پسیو، یک فیلتر بالا گذر اکتیو مرتبه اول را نیز میتوان به سادگی به فیلترهای از مرتبه بالاتر تبدیل کرد. برای تبدیل یک فیلتر بالا گذر اکتیو مرتبه اول به یک فیلتر بالا گذر اکتیو مرتبه دوم، میتوان یک شبکه RC را در مسیر ورودی مدار اضافه کرد.
در تصویر زیر نمایی از یک مدار فیلتر بالا گذر اکتیو مرتبه دوم نشان داده شده است.
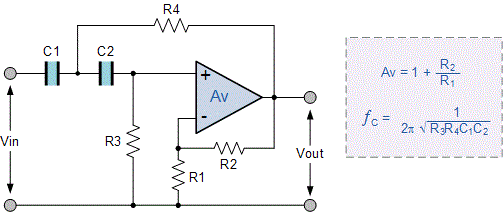
پاسخ فرکانسی فیلتر بالا گذر اکتیو مرتبه دوم، مشابه با پاسخ فرکانسی فیلتر بالا گذر مرتبه اول است و فقط در این تفاوت دارد که رول آف باند توقف دو برابر فیلتر مرتبه اول و برابر با $$ 40 \; dB / decade $$ یا $$ 12 \; dB / octave $$ است. بنابراین گامهای مورد نیاز برای طراحی یک فیلتر بالا گذر اکتیو مرتبه دو کاملا مانند قبل است.
توجه کنید که فیلترهای بالا گذر اکتیو از مرتبه بالاتر مانند سه، چهار، پنج و ... را نیز میتوان به سادگی و از طریق اتصال آبشاری فیلترهای مرتبه اول و مرتبه دوم ایجاد کرد. به عنوان مثال، میتوان یک فیلتر بالا گذر اکتیو مرتبه سه را با اتصال سری یک فیلتر مرتبه اول و یک فیلتر مرتبه دوم پیادهسازی کرد.
بنابراین میتوان گفت که یک فیلتر بالا گذر اکتیو با عدد مرتبه زوج، فقط از فیلترهای مرتبه دو ایجاد میشود، در حالی که یک فیلتر بالا گذر اکتیو از عدد مرتبه فرد، با یک فیلتر بالا گذر اکتیو مرتبه یک در ورودی شروع میشود. در تصویر زیر نمایی از نحوه اتصال آبشاری فیلترهای بالا گذر اکتیو برای تشکیل فیلترهای بالا گذر مرتبه بالاتر نشان داده شده است.
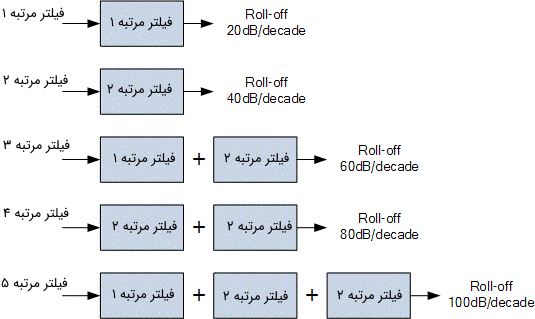
اگرچه به لحاظ تئوری هیچ محدودیتی برای مرتبه یک فیلتر در ساخت وجود ندارد، اما باید به این نکته توجه کرد که هر چه مرتبه فیلتر بالاتر میرود، متناسب با آن سایز فیلتر نیز بزرگتر میشود. همچنین، با افزایش مرتبه یک فیلتر بالا گذر اکتیو، دقت (Accuracy) آن فیلتر کاهش مییابد. دلیل کاهش دقت، افزایش مقدار اختلاف بین باند توقف پاسخ واقعی و باند توقف پاسخ تئوری است.
اگر مقاومتهای تعیین کننده فرکانس همگی برابر ($$ R _ 1 = R _ 2 = R _ 3 $$) و نیز خازنهای مشخص کننده فرکانس با یکدیگر برابر باشند ($$ C _ 1 = C _ 2 = C _ 3 $$)، آنگاه فرکانس قطع برای تمام فیلترهای بالا گذر اکتیو از هر مرتبهای با یکدیگر برابر خواهند بود. البته بهره کلی یک فیلتر بالا گذر از مرتبه بالا ثابت است؛ زیرا تمام المانهای تعیین کننده فرکانس با یکدیگر برابر هستند.
اگر این مطلب برای شما مفید بوده است، مطالب و آموزشهای زیر نیز برای مطالعه بیشتر به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش الکترونیک ۳
- مجموعه آموزشهای مهندسی مخابرات
- آموزش طراحی فیلتر و سنتز مدار
- تقویت کننده لگاریتمی و آنتی لگاریتمی — از صفر تا صد
- اسیلاتور کنترل شده با ولتاژ (VCO) — از صفر تا صد
- فیلتر میان گذر پسیو — از صفر تا صد
^^










