مدار انتگرال گیر RC — به زبان ساده (+ دانلود فیلم آموزش رایگان)
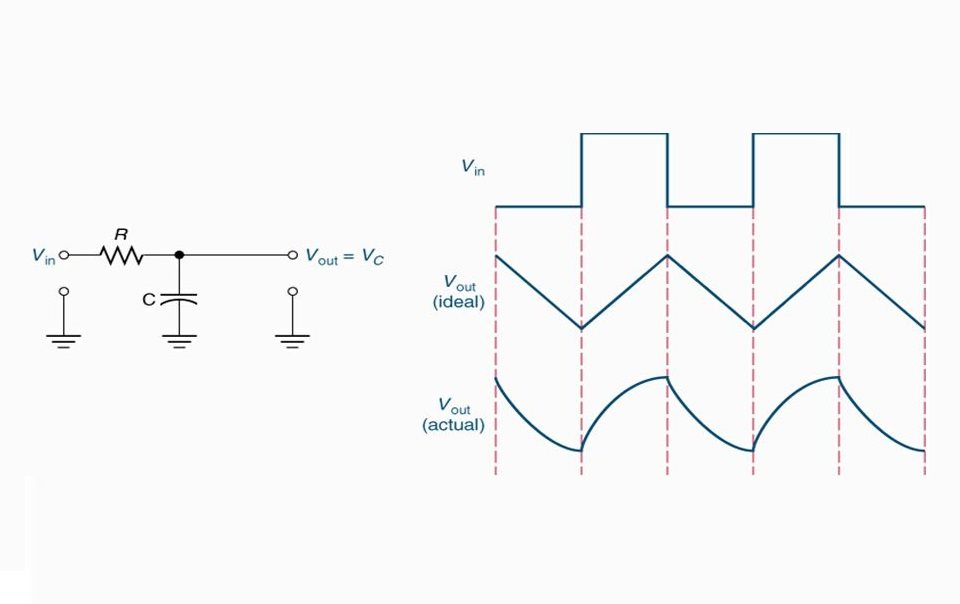
در الکترونیک، مدار RC کاربردهای فراوانی از مدارهای شارژ-دشارژ تا فیلترهای مرتبه بالا دارد. این مدار، با دو قطعه مقاومت و خازن، مدار سادهای به نظر میرسد، اما بسته به نوع و فرکانس سیگنال ورودی، رفتار و پاسخ بسیار متفاوتی خواهد داشت. در یک مدار انتگرال گیر RC پسیو، ورودی به مقاومت وصل شده و ولتاژ خروجی از خازن گرفته میشود.
مدار انتگرال گیر RC
یک مدار RC پسیو، چیزی جز یک مقاومت سری با خازن نیست که دارای یک مقاومت ثابت سری با راکتانسی وابسته به فرکانس است. با توجه به رابطه $$X_C = 1/(2 \pi f C)$$، در فرکانسهای پایین، راکتانس $$X_c$$ خازن زیاد و در فرکانسهای بالا، مقدار آن کم است.
اگر سیگنال ورودی، یک شکل موج سینوسی باشد، انتگرالگیر RC مانند یک فیلتر پایین گذر (LPF) در بالای نقطه قطع یا فرکانس قطع یا گوشه متناظر با ثابت زمانی شبکه سری عمل میکند. بنابراین، وقتی یک سیگنال با شکل موج سینوسی خالص را به انتگرالگیر RC اعمال کنیم، مدار مانند یک فیلتر پایین گذر عمل میکند و خروجی را در بالای نقطه فرکانس قطع محدود میسازد.
همانطور که میدانیم، ثابت زمانی مدار $$RC$$ رابطه بین مقاومت و ظرفیت را نسبت به زمان نشان میدهد و تناسب مستقیم با مقاومت $$R$$ و خازن $$C$$ دارد.
بنابراین، نرخ شارژ یا دشارژ به ثابت زمانی $$T=RC$$ وابسته است.
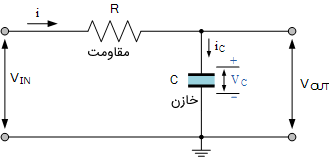
در یک مدار انتگرالگیر $$RC$$، سیگنال ورودی به مقاومت اعمال میشود و خروجی از خازن گرفته میشود. بنابراین، $$ V_{OUT}$$ برابر با $$ V_C$$ است. از آنجایی که خازن یک قطعه وابسته به فرکانس است، مقدار بارهای روی صفحات آن، برابر با انتگرال زمانی جریان است. این بدین معنی است که زمان مشخصی طول میکشد که خازن کاملاً شارژ شود، زیرا خازن نمیتواند به صورت آنی شارژ گردد و شارژ آن به صورت نمایی است.
بنابراین، جریان خازن را میتوان به صورت زیر نوشت:
$$ \large i _ {C(t)} = C \frac {dv_{C(t)}}{dt}$$
معادله اساسی $$ i_C= C(dv_C / dt)$$ را میتوان با تغییر لحظهای بار $$Q$$ نسبت به زمان با معادله $$i_C=dQ/dt$$ توصیف کرد که در آن، بار برابر با حاصلضرب ظرفیت در ولتاژ است: $$Q=C \times V_C$$.
نرخی که خازن شارژ یا دشار میشود، نسبت مستقیمی با مقدار مقاومت و ظرفیت دارد که ثابت زمانی مدار را نشان میدهد. بنابراین، ثابت زمانی یک مدار انتگرالگیر RC، یک بازه زمانی برابر با حاصلضرب $$R$$ در $$C$$ است.
ظرفیت خازن $$ Q / V_C$$ است، که در آن $$Q$$ شارش جریان $$i$$ در زمان $$t$$ است و با ضرب $$ i \times t $$ بیان میشود و واحد آن کولن (Coulomb) است. همچنین، با توجه به قانون اهم میدانیم که ولتاژ $$v$$ برابر با ضرب جریان در مقاومت $$ i \times R$$ است. با جایگذاری این مقدار در معادله ثابت زمانی RC، ثابت زمانی به صورت زیر به دست میآید:
$$ \large RC = R \frac { Q} { V} = R \frac {i \times T}{i \times R} = T $$
$$ \large T = RC $$
ثابت زمانی مدار انتگرالگیر RC بر حسب ثانیه است و آن را با حرف یونانی $$ \tau $$ نشان میدهند. لازم به ذکر است که ثابت زمانی، زمان لازم (برحسب ثانیه) را برای آن نشان میدهد که شارژ خازن به $$ 63.2 \, \%$$ ولتاژ ماکزیمم برسد یا به اندازه $$ 36. 8 \, \%$$ مقدار ماکزیمم ولتاژ تخلیه شود.
گفتیم که خروجی مدار انتگرالگیر RC برابر با ولتاژ خازن است. این ولتاژ، متناسب با بار $$Q$$ است که در خازن ذخیره میشود: $$ Q = V \times C$$.
در نتیجه، ولتاژ خروجی، انتگرال ولتاژ ورودی است و مقدار آن به مقادیر $$R$$ و $$C$$ و در نتیجه، ثابت زمانی بستگی دارد.
در بالا گفتیم که جریان خازن را میتوان بر حسب تغییرات بار $$Q$$ نسبت به زمان توصیف کرد. بنابراین، طبق یک قاعده کلی از حساب دیفرانسیل، مشتق $$Q$$ نسبت به زمان ($$dQ/dt$$) و در نتیجه $$ i = d Q/ dt$$ را میتوان با رابطه زیر بیان کرد:
$$ \large Q = \int i dt $$
از آنجایی که ورودی به مقاومت اعمال میشود، جریان مشابهی از مقاومت و خازن عبور میکند ($$ i_R = i_C$$) و افت ولتاژ $$V_R$$ را در دو سر مقاومت ایجاد خواهد کرد. جریان برابر است با:
$$ \large i ( t) = \frac {V _{IN} } {R} = \frac {V_R} {R} = C\frac {dv} {dt} $$
در نتیجه، ولتاژ خروجی به صورت زیر خواهد بود:
$$ \large V _ {OUT} = V_C = \frac {Q} {C} = \frac {\int i dt} {C} = \frac {1} {C} \int i (t) dt$$
از آنجایی که $$ i = V_{In}/ R$$، با جایگذاری و کمی تغییرات، تابع $$ V _ {OUT}$$ به صورت زیر خواهد بود:
$$ \large V _ {OUT} = \frac {1} {C} \int \left ( \frac { V_{IN} }{R} \right) dt = \frac {1} {RC} \int V _ {IN} dt $$
بنابراین، به عبارت دیگر، خروجی یک مدار انتگرالگیر RC، که برابر با ولتاژ خازن است، برابر با انتگرال ولتاژ ورودی $$V_{IN}$$ با ضریب $$ 1 / RC$$ خواهد بود.
با فرض شرایط اولیه صفر، $$V _{OUt} = 0$$ و ولتاژ ورودی $$ V _ {IN}$$ ثابت است و ولتاژ خروجی به صورت زیر بیان میشود:
$$ \large V _{OUT} = \frac {1 } {RC} \int _0 ^ t V _{IN(t)} dt $$
انتگرالگیر RC تکپالسه
وقتی یک پالس ولتاژ پلهای به ورودی انتگرالگیر RC اعمال کنیم، خازن از طریق مقاومت $$R$$ شارژ میشود. البته، ولتاژ خروجی به سرعت تغییر نمیکند و به صورت نمایی افزایش مییابد. نرخ شارژ خازن برابر با ثابت زمانی $$ \tau = R C $$ است.
میدانیم که سرعت شارژ و دشارژ با ثابت زمانی RC تعیین میشود. اگر یک پالس ولتاژ پله ایدهآل به مدار اعمال کنیم، ولتاژ خازن در هنگام شارژ به صورت زیر خواهد بود:
$$ \large V _ {C ( t ) } = V \left ( 1 - e ^ { - \left ( \frac { t } { R C } \right ) } \right ) $$
در حالت تخلیه یا دشارژ نیز داریم:
$$ \large V _ {C ( t ) } = V \left ( e ^ { - \left ( \frac { t } { R C } \right ) } \right ) $$
بنابراین، اگر فرض کنیم ولتاژ خازن برابر با یک ولت است، میتوانیم درصد شارژ یا دشارژ خازن را برای هر ثابت زمانی R مطابق جدول زیر رسم کنیم.
| ثابت زمانی | شارژ خازن | تخلیه خازن |
| $$ T $$ | درصد شارژ | درصد تخلیه |
| $$ 0.5$$ | $$39.4\%$$ | $$60.6 \%$$ |
| $$ 0.7$$ | $$50\%$$ | $$50 \%$$ |
| $$1$$ | $$63.2\%$$ | $$36.7 \%$$ |
| $$2$$ | $$86.4\%$$ | $$13.5 \%$$ |
| $$3$$ | $$95.0\%$$ | $$4.9 \%$$ |
| $$4$$ | $$98.1\%$$ | $$1.8 \%$$ |
| $$5$$ | $$99.3 \% $$ | $$0.67 \%$$ |
همانطور که میبینیم بعد از گذشت $$5$$ ثابت زمانی یا بیشتر از آن، خازن کاملاً شارژ یا کاملاً دشارژ میشود.
مثال
مدار شکل زیر را در نظر بگیرید.
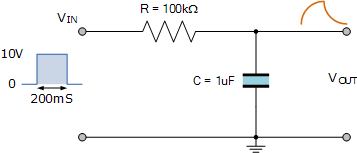
ثابت زمانی مدار برابر است با:
$$ \large RC = 100 \, \text {k} \Omega \times 1\, \mu \text {F} = 100 \, \text {ms} $$
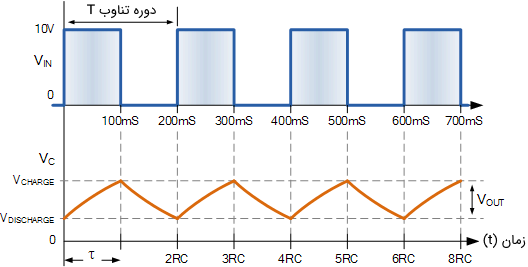
اگر یک ولتاژ پله را به مدت $$200$$ ثانیه به مدار اعمال کنیم، با توجه به جدول بالا، به اندازه $$86.4 \%$$ مقدار شارژ کاملش میرسد. اگر این پالس دامنهای به اندازه $$10$$ ولت داشته باشد، قبل از آنکه خازن دوباره تخلیه شود و انرژی آن از طریق مقاومت به منبع منتقل گردد، ولتاژ برابر با $$8.64$$ ولت خواهد بود، زیرا پالس ورودی به صفر بر میگردد.
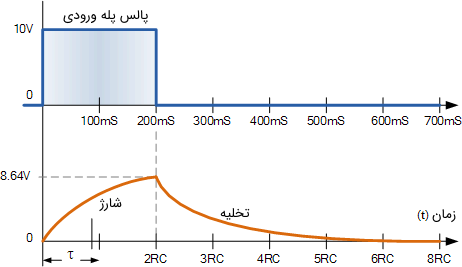
باید توجه کرد که مقدار اولیه خازن در حالت دشارژ برابر با $$8.64$$ ولت (دو ثابت زمانی) است (نه $$10$$ ولت).
همانطور که میبینیم، از آنجایی که ثابت زمانی RC ثابت است، هر تغییر در پهنای پالس ورودی بر خروجی مدار انتگرالگیر RC تأثیر خواهد گذاشت. اگر پهنای پالس افزایش یابد و به $$5RC$$ یا بزرگتر از آن برسد، آنگاه شکل خروجی شبیه خروجی خواهد بود، زیرا ولتاژ خروجی برابر با ولتاژ ورودی خواهد شد.
البته اگر پهنای پالس به کمتر از $$5RC$$ کاهش یابد، خازن به صورت جزئی شارژ شده و به مقدار ماکزیمم ولتاژ ورودی نمیرسد. در نتیجه ولتاژ خروجی کوچکتر از ولتاژ ورودی خواهد بود، زیرا ولتاژ خروجی متناسب با انتگرال ولتاژ ورودی است.
بنابراین، اگر فرض کنیم یک ورودی پالسی برابر با یک ثابت زمانی $$1RC$$ باشد، بین $$0$$ و $$10$$ ولت شارژ و دشارژ نمیشود، بلکه بین $$63.2 \%$$ و $$38.7 \%$$ ولتاژ دو سر خازن در زمان تغییر شارژ و دشارژ میشود. این مقادیر با استفاده از ثابت زمانی $$RC$$ تعیین شدهاند.
انتگرالگیر RC به عنوان ژنراتور سینوسی
در بخش قبل دیدیم که مدار انتگرالگیر RC با اعمال یک پالس ورودی، یک شکل موج مثلثی را نتیجه خواهد داد. اما اگر این عملیات را برعکس کنیم و یک شکل موج مثلثی را به ورودی اعمال کنیم، آیا یک شکل موج پالسی یا مربعی در خروجی خواهیم داشت؟
اگر ورودی مدار انتگرالگیر RC یک شکل موج پالسی باشد، خروجی یک شکل موج مثلثی است. اما اگر یک شکل موج مثلثی را به مدار اعمال کنیم، خروجی به دلیل انتگرالگیری زمانی از سیگنال رمپ یا شیب، یک شکل موج سینوسی خواهد بود.
راههای مختلفی برای تولید یک شکل موج سینوسی وجود دارد، اما یک راه ساده و ارزان برای تولید الکترونیکی شکل موج سینوسی، استفاده از یک جفت مدار انتگرالگیر RC پسیو است که مطابق شکل زیر به صورت سری به یکدیگر متصل شدهاند.
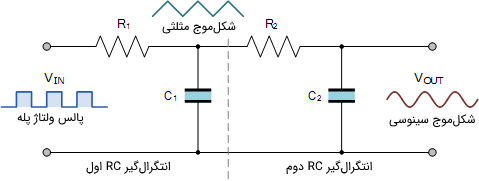
انتگرالگیر RC نخست، ورودی پالسی اصلی را به یک شکلموج مثلثی تبدیل میکند. این شکلموج خروجی، ورودی انتگرالگیر RC دوم است. انتگرالگیر دوم نقاط شکستگی شکلموج مثلثی را هموار کرده و آن را به یک شکلموج سینوسی تبدیل میکند.
جمعبندی
دیدیم که مدار انتگرالگیر RC، اساساً یک مدار فیلتر پایین گذر RC است که وقتی یک پالس ولتاژ پله به آن اعمال میشود، خروجی آن رابطه مستقیمی با انتگرال ورودی دارد.
با اتصال دو مدار انتگرالگیر RC به یکدیگر به صورت سری، میتوان اثر انتگرال دوگانه روی پالس ورودی گذاشت. نتیجه این انتگرالگیری دوگانه این است که انتگرالگیر نخست پالس ولتاژ پله را به یک شکل موج مثلثی تبدیل میکند و انتگرالگیر دوم، یک شکل موج سینوسی را از شکل موج مثلثی تولید خواهد کرد. البته دامنه این شکل موج سینوسی خروجی، نسبت به دامنه ورودی به اندازه قابل توجهی کاهش مییابد.
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
- دو قطبی در مدارهای الکتریکی — به زبان ساده
- تزویج در مدارهای الکتریکی — مفاهیم اصلی
- نوسان در مدارهای الکتریکی — از صفر تا صد
^^











امکانش هست با ترکیبش با ترانزیستور مبدل digital to analog صوتی بسازیم ؟