شبیه سازی مدار در متلب – راهنمای کاربردی (+ دانلود فیلم آموزش رایگان)
در آموزشهای پیشین مجله فرادرس، با برنامهنویسی در متلب و اصول شبیهسازی در سیمولینک آشنا شدیم. در این آموزش، شبیه سازی مدار در متلب و سیمولینک را در قالب مثال یک مدار RLC بیان میکنیم.
مدلسازی مدار RLC
یک مدار RLC در شکل ۱ نشان داده شده است.

ابتدا معادلات مدار RLC را به دست میآوریم. در مدار مورد نظر، جریان رابطه مستقیمی با افت ولتاژ سلف دارد؛
بدین صورت که مشتق ولتاژ متناسب با جریان گذرنده از آن است. بنابراین، میتوانیم دو معادله دیفرانسیل مرتبه اول و سپس با اعمال قانون ولتاژ کیرشهف (KVL)، معادله ولتاژ حلقه را بنویسیم.
دو متغیر و متغیرهای حالت نامیده میشوند. معادلات بالا، به عنوان معادلات جبری دینامیکی (DAE) شناخته میشوند. با جایگذاری مقدار در معادله جبری، به دو معادله دیفرانسیل معمولی (ODE) خواهیم رسید:
در معادلات بالا، مشتق متغیرهای حالت برحسب خود حالتها و ورودی بیان شده است.
توصیف عمومی سیستم بالا به صورت زیر است:
که در آن، ورودی و بردار متغیرهای حالت است.
در مدار RLC بالا، و . مدار RLC یک سیستم خطی است و میتوانیم مدل فضای حالت خطی زیر را برای آن بنویسیم:
خروجی مدل را نیز به صورت زیر تعریف میکنیم:
که در آن، یک ماتریس همانی است و .
اگر فقط جریان را به عنوان خروجی در نظر بگیریم، داریم:
شبیهسازی در پایتون
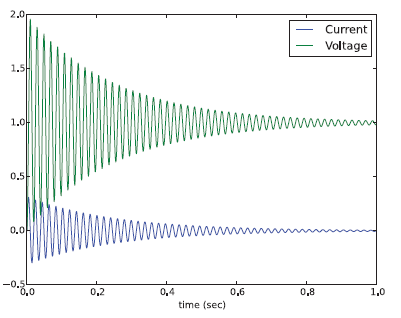
برای مقایسه، شبیهسازی را در پایتون نیز انجام میدهیم. کد پایتون زیر برای شبیهسازی مدار RLC نوشته شده است. در این برنامه، ابتدا تابعی برای محاسبه مشتقهای تعریف شده است.
ورودیهای این تابع پارامترهای RLC، بردار متغیر حالت و منبع ولتاژ هستند. در ادامه برنامه، روش ذوزنقهای رایج برای انتگرالگیری عددی نوشته شده است. در هر گام ، مشتقهای با فراخوانی تابع محاسبه میشوند. بر اساس مشتق، حالت در گامهای بعدی با استفاده از روش اویلر رو به جلو تخمین زده میشود. بر اساس این تخمین، مشتق در گام محاسبه میگردد. با استفاده از دو مشتق، حالت در گام محاسبه خواهد شد.
شکل ۲ نتایج شبیهسازی برنامه پایتون بالا را نشان میدهد.
شبیه سازی مدار در متلب با حل کننده ODE
حلکنندههای ODE متلب محیطی را برای انتگرالگیری عددی فراهم میکنند. تنها کافی است را تعریف کرده و حلکننده را فراخوانی کنیم.
در یک امفایل (m-file) به نام fun_RLC.m، تابعی با نام fun_RLC را برای محاسبه تعریف میکنیم. برای استفاده از حلکنندههای ODE، ابتدا را تعریف میکنیم. در اینجا، را به عنوان یک ورودی پله در نظر میگیریم تا پاسخ پله را مشاهده کنیم.
برنامه اصلی فراخوانی حلکننده ODE به صورت زیر است:
دقت کنید که در حلکنندههای ODE باید نام تابع را برای محاسبه مشتق بردار حالت نوشت. ورودیهای دوم و سوم تابع مدت زمان شبیهسازی و متغیرهای حالت اولیه هستند. همانطور که میبینیم، نتایج شبیهسازی مشابه شکل ۲ است.
شبیهسازی در سیمولینک
در این بخش، دو روش را برای شبیهسازی مدار در سیمولینک بیان میکنیم. البته شبیهسازی را میتوان با کمک کتابخانههایی مانند Simscape Electrical در سیمولینک نیز انجام داد که در این آموزش به آن نمیپردازیم.
تشکیل مدل با تابع توکار Embedded Function
گام مهم فرایند تشکیل مدل شناسایی بردار متغیرهای حالت و محاسبه مشتق از بردار ورودی و خودِ است. پس از آن، حالت و مشتق آن با یک انتگرالگیر با هم مرتبط میشوند. با تنظیم حالت اولیه در انتگرالگیر، مدل آماده اجرا خواهد بود.
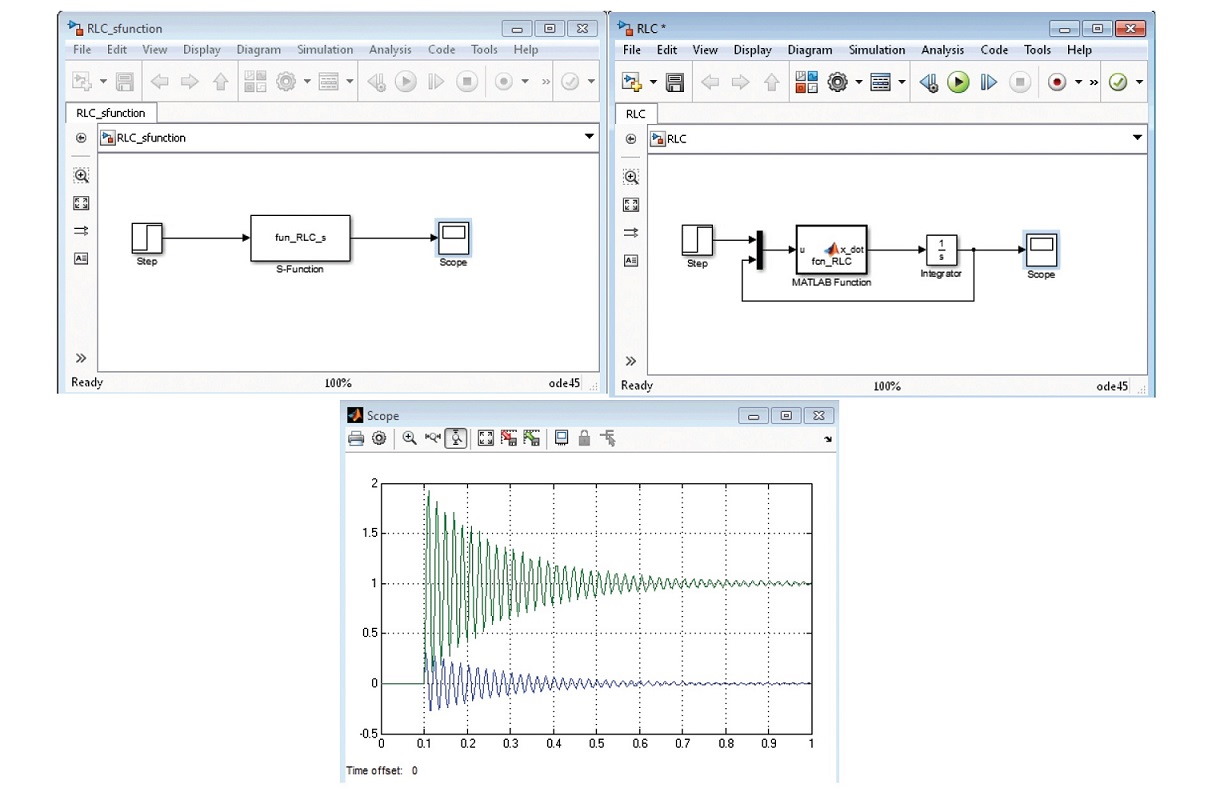
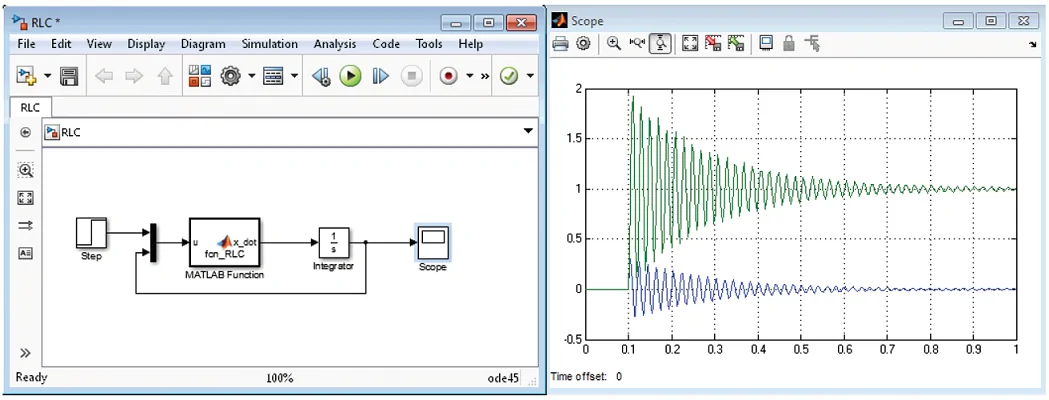
شکل ۳ بلوکهای تشکیل دهنده یک مدل دینامیکی را نشان میدهند که به صورت توصیف میشود. از یک انتگرالگیر نیز برای برقراری ارتباط حالت و مشتق آن استفاده شده است. ورودی انتگرالگیر باید باشد، در حالی که خروجی آن، است. با استفاده از یک تابع توکار (Embedded Function) متلب محاسبه میشود. ورودی تابع یک بردار شامل منبع ولتاژ و متغیرهای حالت است. و به بلوک Mux وارد میشوند و یک بردار را تولید میکنند. درون تابع fcn_RLC، و از هم تفکیک شدهاند. توجه کنید که ورودی دیگری به نام par نیز وجود دارد که یک ساختار (Structure) شامل مقادیر ، و است.
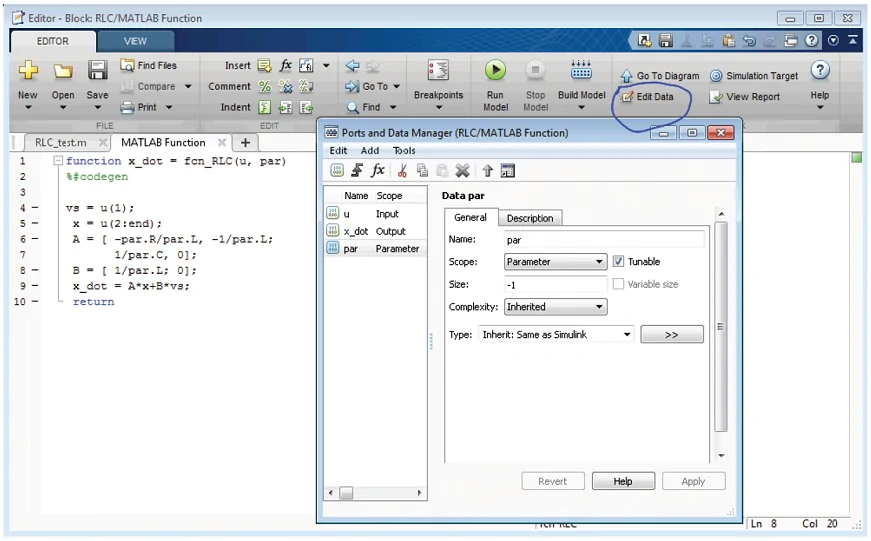
همانطور که در شکل ۴ نشان داده شده است، متلب par را به عنوان یک ورودی در نظر میگیرد. برای آنکه par به عنوان یک پارامترِ مشخص در نظر گرفته شود، باید از گزینه Edit Data استفاده کرده و آن را به عنوان یک پارارمتر انتخاب کنیم.
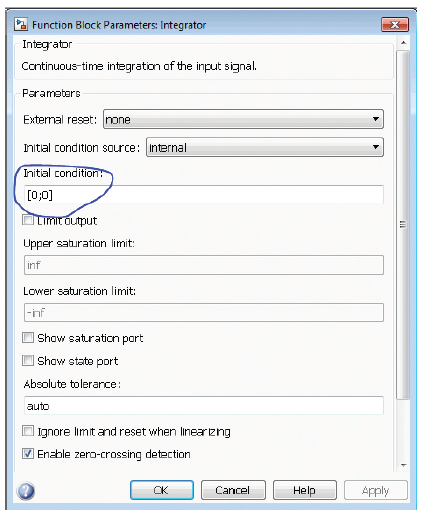
یک مورد مهمتر، تنظیم صحیح مقادیر اولیه انتگرالگیر، مخصوصاً اندازه است. در این مثال، باید یک بردار شامل مقدار جریان اولیه و ولتاژ اولیه باشد. بنابراین، مقدار بردار اولیه را [0,0] یا (zeros(2,1 قرار میدهیم.
در مرحله شبیهسازی، میتوانیم در قسمت تنظیمات سیمولینک، دوره شبیهسازی، روش انتگرالگیری عددی و اندازه گام را تعیین کنیم.
 " width="423" height="516">
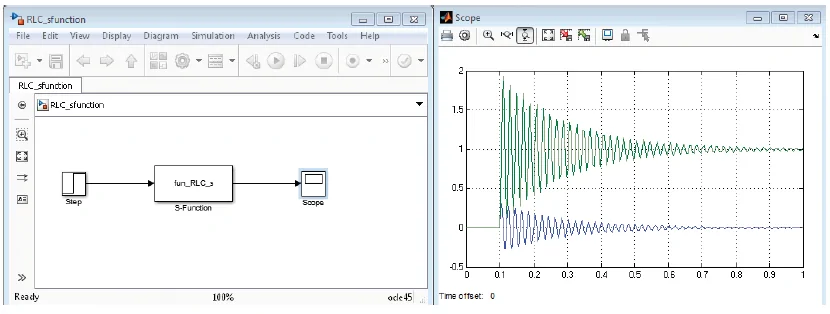
" width="423" height="516">تشکیل مدل بر اساس S-function
در رویکرد S-function، کل سیستم در یک بلوک تعریف میشود که در شکل ۶ نشان داده شده است. یک S-function قالب مشخص و ثابتی برای تعریف ابعاد سیستم، حالت اولیه، مشتق حالت و... دارد. برای مدار RLC مورد نظر، از قالب سیستم پیوسته استفاده میکنیم.
S-function سه مورد دارد که باید به آنها توجه کنیم: (الف) مقداردهی اولیه، (ب) محاسبه مشتق و (ج) تعریف خروجی. تنظیمات بردار حالت اولیه ورودی، خروجی و حالت در ابتدای کار تنظیم میشوند. این کار با تابع mdlInitializeSizes انجام میشود. کار دوم، محاسبه مشتق است که با کمک تابع mdlDerivatives انجام میگیرد. کار سوم، تعریف خروجی است که با تابع mdlOutputs آن را انجام میدهیم. برنامه S-function به صورت زیر است:
دستورهای متلب برای شبیهسازی سیستمهای خطی
روشهای شبیهسازی که در بخش قبل به آنها اشاره کردیم، به یک سیستم دینامیکی عمومی قابل اعمال هستند. برای سیستمهای خطی، میتوانیم مستقیماً از دستورهای متلب به منظور شبیهسازی استفاده کنیم. جعبهابزار کنترل متلب توابع زیادی برای تحلیل و شبیهسازی سیستمهای خطی نامتغیر با زمان (LTI) دارد. با نوشتن چند خط دستور میتوان مدل یک سیستم LTI را ساخت و آن را در حوزه زمان شبیهسازی کرد. با کمک این دستورها، نیازی به نوشتن برنامههای طولانی نداریم.
در ادامه، با در نظر گرفتن مدار RLC، مدل LTI آن را در قالب تابع تبدیل یا فضای حالت خواهیم ساخت.
تعریف مدلهای خطی
اولین گام، تعریف مدل LTI مدار RLC است. در بخشهای قبل، مدل این مدار را در فرم زیر به دست آوردیم:
با تعریف ، ، و این مدل فضای حالت را میتوان، در یک خط، به صورت زیر تعریف کرد:
تابع تبدیل مدل نیز به صورت زیر به دست میآید:
به فرم یک تابع تبدیل لاپلاس است.
یک رویکرد دیگر تعریف مدل در حوزه فرکانس است. بدین منظور، مدل امپدانس را برای هر عنصر مدار بررسی میکنیم. مدل امپدانس اصطلاحی است که نسبت نِمُو یا تغییر ولتاژ به نمو جریان را در حوزه فرکانس توصیف میکند. تکنیک مدلسازی امپدانس، یک تکنیک مدلسازی پرکاربرد در تحلیل مبدلهای الکترونیک قدرت است. مدل امپدانس مقاومت همان و مدل امپدانس سلف و خازن نیز، به ترتیب، و است.
بنابراین، میتوانیم عبارت تغییر جریان را با قانون اهم به دست آوریم. تابع تبدیل به به صورت زیر است:
در یک سیستم خطی، هنگام توصیف تابع تبدیل، معمولاً از نوشتن چشمپوشی میکنیم. همچنین داخل پرانتز را نمینویسیم.
توابع تبدیل بالا روابط ورودی/خروجی جریان، ولتاژ خازن و ولتاژ سلف در برابر ولتاژ ورودی را تعریف میکنند. این توابع تبدیل را میتوان با استفاده از عملگر لاپلاسِ s در متلب بیان کرد:
خط دوم رابطه ورودی/خروجی ولتاژ و جریان منبع را تعریف میکند. خط سوم نیز رابطه ورودی/خروجی ولتاژ منبع و ولتاژ خازن را معرفی میکند. خط چهارم برای تعریف رابطه ورودی/خروجی بین ولتاژ منبع و ولتاژ سلف است.
پاسخ زمانی
با تعریف مدل، میتوانیم شبیهسازی حوزه زمان را با استفاده از دستورهای متلب انجام دهیم.
مثال ۱: پاسخ زمانی جریان را وقتی ولتاژ منبع یک پاسخ پله باشد.
حل: پاسخ پله را میتوان با استفاده از دستور step متلب به دست آورد. برنامه متلب مورد نظر به صورت زیر است:
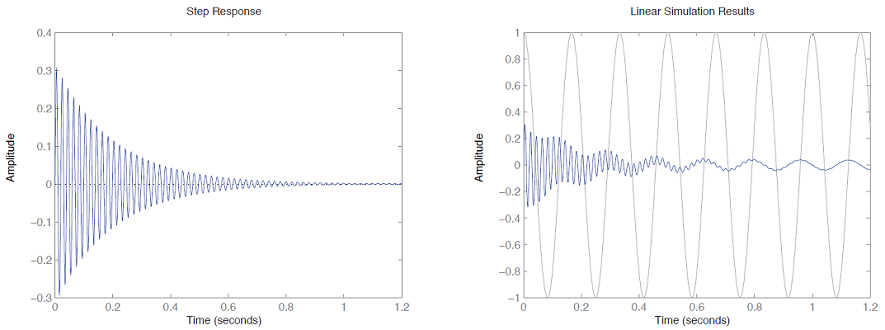
مثال ۲: پاسخ حوزه زمان جریان را وقتی که ولتاژ منبع از ۰ به یک ولتاژسینوسی با فرکانس ۶ هرتز تغییر میکند، به دست آورید.
حل: به طور کلی، میتوانیم از lsim برای شبیهسازی پاسخ به هر ورودی استفاده کنیم. کد مربوط به این مثال به صورت زیر است:
شکل ۷ نمودارهای مربوط بو دو دستور step و lsim را نشان میدهد.
تحلیل سیستم خطی
در یک سیستم تکورودی-تکخروجی (SISO)، میتوانیم تحلیل سیستم خطی را با استفاده از دستور bode متلب برای به دست آوردن نمودارهای بُد، دستور pole برای یافتن قطبها، دستور zero برای یافتن صفرهای سیستم و pzmap برای پیدا کردن قطبها و صفرها در فضای حقیقی-موهومی انجام دهیم.
شکل ۸ با استفاده از دستور زیر رسم شده است.
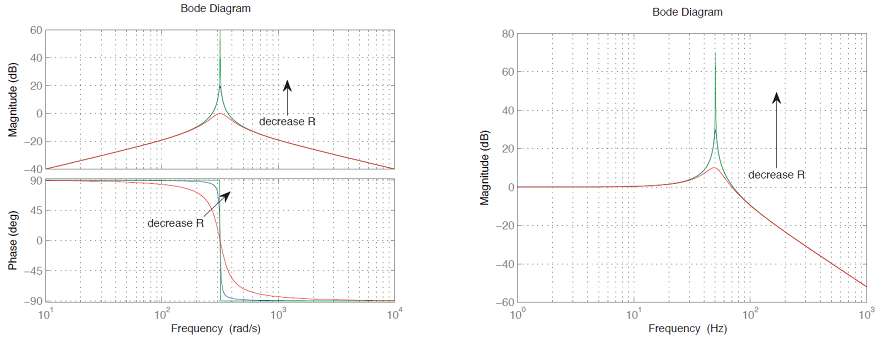 و " width="884" height="340">
و " width="884" height="340">نمودارهای بُد (اندازه) شکل ۸ مقدار پیک ۵۰۰ هرتز را نشان میدهند. این موضوع نشان دهنده وجود نوسانهایی با فرکانس ۵۰۰ هرتز است. اگر مقاومت کوچکتر باشد، مقدار این پیک محسوستر خواهد بود. هرچه پیک نمودار اندازه بُد بیشتر باشد، نوسان در فرکانس ۵۰۰ هرتز میرایی کمتری خواهد داشت. با مقایسه شکلهای ۷ و ۲ میتوان دریافت که فرکانس نوسانها تقریباً ۵۰۰ هرتز است.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش شبیه سازی با سیمیولینک Simulink
- مجموعه آموزشهای برنامهنویسی متلب (MATLAB)
- گنجینه آموزشهای شبیه سازی با سیمیولینک (Simulink)
- کاربرد تبدیل لاپلاس در تحلیل مدار — به زبان ساده
- رسم نمودار دو بعدی در متلب - از صفر تا صد
- دوقطبی در مدارهای الکتریکی — به زبان ساده
^^












سلام . تشکر .خیلی خوب و عالی
سلام ایمان عزیز.
خوشحالیم که همراه مجله فرادرس هستید.
سالم و موفق باشید.