سری فوریه سینوسی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

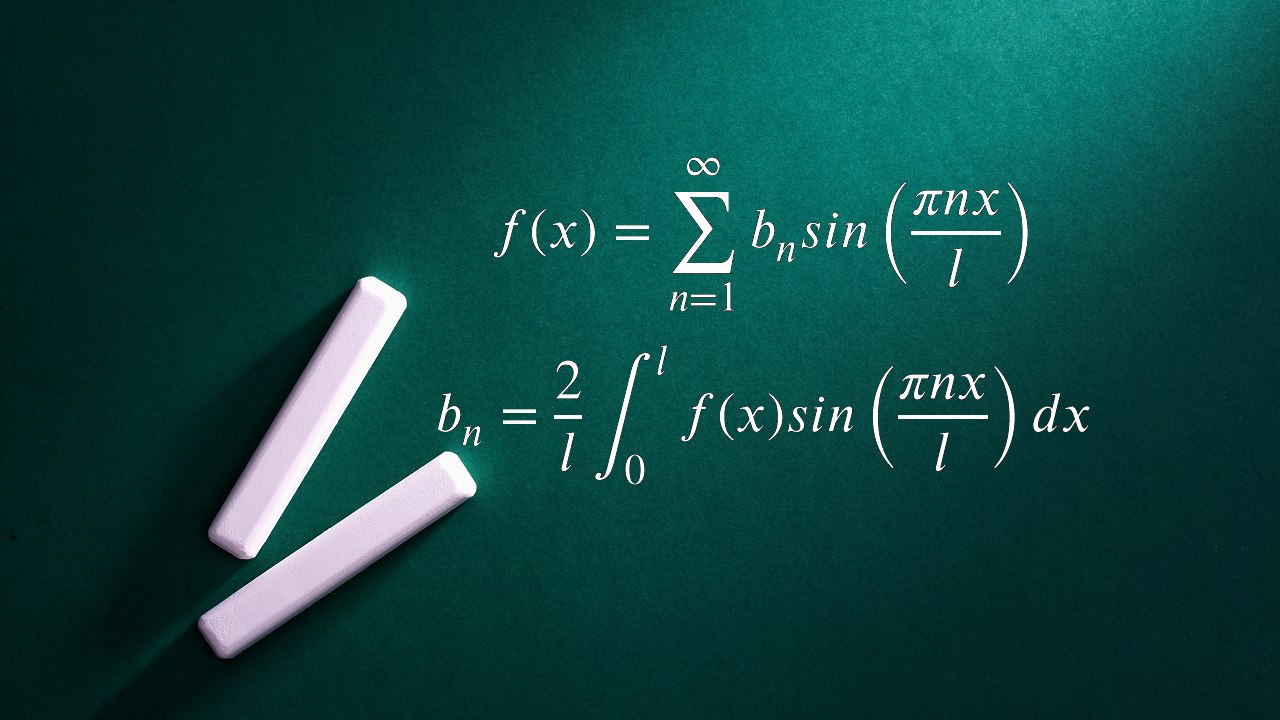
در آموزش‌های قبلی مجله فرادرس، درباره سری فوریه و تبدیل فوریه بحث کردیم. در این آموزش قصد داریم مفاهیم سری فوریه سینوسی را بیان کنیم.

در ابتدا بسط تیلور را در نظر بگیرید. بسط تیلور،‌ یک نمایش سری از تابع $$f(x)$$ است. بسط تیلور تابع $$f(x)$$‌ در نقطه $$x=a$$، سری توانی توابع $$x-a$$ است. این بسط به صورت زیر نوشته می‌شود:

$$f\left( x \right) = \sum\limits_{n = 0}^\infty {\frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{{\left( {x - a} \right)}^n}}$$

سری فوق، در بازه $$\left| {x - a} \right| < R$$ به تابع $$f(x)$$ همگرا می‌شود.

یکی از شرایط لازم برای نوشتن بسط تیلور آن است که مشتقات تابع $$f(x)$$ ار همه درجات روی $$x=a$$ موجود باشد. به عبارت دیگر $${f^{\left( n \right)}}\left( a \right)$$ به ازای $$n = 0,1,2,3, \ldots$$ وجود داشته باشد. اگر همه مشتقات تابع $$f(x)$$ وجود نداشته باشد، نوشتن بسط تیلور برای تابع مشکل می‌شود.

این مشکل و چند مشکل اساسی دیگر، نشان می‌دهد که بسط تیلور، روش مناسبی برای نمایش سری یک تابع نیست. در بسیاری از موارد، این بسط مناسب است و احتیاجی به استفاده از سری‌های متفاوت نیست. اما در برخی موارد، انواع دیگری از سری ترجیح داده می‌شود. در این آموزش، به بررسی یک نمایش سری دیگر از تابع می‌پردازیم.

سری فوریه سینوسی

فرض کنید تابع $$f(x)$$، یک تابع فرد است. یعنی:

$$f(-x) = -f(x)$$

فیلم آموزش ریاضی مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

از آنجا که تابع $$f(x)$$ یک تابع فرد است، منطقی است که این تابع به صورت سری سینوسی نوشته شود. زیرا توابع سینوسی نیز فرد هستند.

تابع $$f(x)$$، روی بازه $$- L \le x \le L$$ تعریف شده است. سری فوریه سینوسی این تابع به صورت زیر نوشته می‌شود:

$$f(x) =\sum\limits_{n = 1}^\infty {{B_n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)}$$
(معادله (۱

این سری در بازه $$- L \le x \le L$$ به تابع $$f(x)$$ همگرا است.

تفاوت‌های سری فوریه سینوسی و بسط تیلور

ذکر این نکته ضروری است که سری فوریه سینوسی بر خلاف سری تیلور، همواره به تابع $$f(x)$$ در یک بازه همگرا می‌شود. این بازه به تابع وابسته نیست. اما در سری تیلور، بازه‌ای برای همگرایی بسط وجود ندارد.

مسئله دوم این است که سری سینوسی بر خلاف سری تیلور، شامل توان‌های توابع سینوسی نمی‌شود، بلکه آرگومان‌های توابع سینوسی سری تشکیل می‌دهند.

در نهایت، لازم نیست آرگومان توابع سینوسی حتما به صورت $$\frac{{n\pi x}}{L}$$ باشد، اما این انتخاب آرگومان دلایل متفاوتی دارد. یکی از این دلایل، استفاده از سری سینوسی با آرگومان مطرح شده در حل معادلات دیفرانسیل با مشتقات جزئی است.

دلیل دیگر استفاده از این آرگومان، متعامد بودن توابع سینوسی در بازه $$- L \le x \le L$$ است. به عبارت دیگر، توابع به کار رفته و بازه انتخاب شده برای توابع فوریه سینوسی به نوعی با یکدیگر مرتبط هستند. با تغییر آرگومان، باید بازه همگرایی را نیز تغییر داد تا تعامد توابع سینوسی (با آرگومان‌های متفاوت) حفظ شود.

محاسبه ضرایب سری فوریه سینوسی

اگر دو طرف معادله (۱) را در $$\sin \left( {\frac{{m\pi x}}{L}} \right)$$ ضرب کنیم، خواهیم داشت:

$$f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right) = \sum\limits_{n = 1}^\infty {{B_n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)}$$

در معادله بالا، $$m$$ یک عدد صحیح ثابت از مجموعه $$\left\{ {1,2,3, \ldots } \right\}$$ است. حال اگر از دو طرف این معادله از $$x = - L$$ تا $$x=L$$ انتگرال‌گیری انجام شود، خواهیم داشت:

$$\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}} = \int_{{\, - L}}^{{\,L}}{{\sum\limits_{n = 1}^\infty {{B_n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)} \,dx}}$$

با تعویض جای انتگرال و سری، به معادله زیر می‌رسیم:

$$\begin{align*}\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}} &= \sum\limits_{n = 1}^\infty {\int_{{\, - L}}^{{\,L}}{{{B_n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}} \\ & = \sum\limits_{n = 1}^\infty {{B_n}\int_{{\, - L}}^{{\,L}}{{\sin \left( {\frac{{n\,\pi x}}{L}} \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}} \end{align*}$$
معادله (۲)

می‌دانیم که توابع سینوسی روی بازه $$- L \le x \le L$$ متعامد هستند. پس داریم:

$$\int_{{ - L}}^{L}{{\sin \left( {\frac{{n\pi x}}{L}} \right)\sin \left( {\frac{{m\pi x}}{L}} \right)\,dx}} = \left\{ {\begin{array}{*{20}{l}}L&{{\mbox{if }}n = m}\\0&{{\mbox{if }}n \ne m}\end{array}} \right.$$

در معادله بالا، اگر $$n = m$$ باشد، انتگرال جواب غیر صفر خواهد داشت. مقدار این انتگرال نیز برابر با $$L$$ است. با ساده کردن معادله (۲) داریم:

$$\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}} = {B_{\,m}}L$$
معادله (۳)

حال اگر دو طرف معادله (۳) به عدد $$L$$ تقسیم شود، ضرایب سری فوریه سینوسی به دست می‌آید:

$${B_{\,m}} = \frac{1}{L}\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}\hspace{0.25in}m = 1,2,3, \ldots$$

می‌دانیم حاصلضرب دو تابع فرد، تابعی زوج است. بنابراین:

$${B_{\,m}} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}\hspace{0.25in}m = 1,2,3, \ldots$$

به طور خلاصه، سری فوریه سینوسی برای تابع فرد $$f(x)$$ که روی بازه $$- L \le x \le L$$ تعریف می‌شود، به صورت زیر خواهد بود:

$$\begin{align*}f\left( x \right) & = \sum\limits_{n = 1}^\infty {{B_n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)} & {B_{\,n}} & = \frac{1}{L}\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\,\,\,\,\,\,\,n = 1,2,3, \ldots \\ & & & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\,\,\,\,\,\,\,n = 1,2,3, \ldots \end{align*}$$

مثال زیر، مفهوم سری فوریه سینوسی را نمایان‌تر می‌کند.

مثال ۱

سری فوریه سینوسی را برای تابع $$f\left( x \right) = x$$ روی بازه $$- L \le x \le L$$ بیابید.

حل: تابع $$f(x)$$، یک تابع فرد است، بنابراین ضرایب سری فوریه سینوسی به صورت زیر به دست می‌آید:

$$\begin{align*}{B_{\,n}} & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{x\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}} = \frac{2}{L}\left. {\left( {\frac{L}{{{n^2}{\pi ^2}}}} \right)\left( {L\sin \left( {\frac{{n\,\pi x}}{L}} \right) - n\pi x\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \right)} \right|_0^L\\ & = \frac{2}{{{n^2}{\pi ^2}}}\left( {L\sin \left( {n\,\pi } \right) - n\pi L\cos \left( {n\,\pi } \right)} \right)\end{align*}$$

با استفاده از دو رابطه $$\sin \left( {n\pi } \right) = 0$$ و $$\cos \left( {n\pi } \right) = {\left( { - 1} \right)^n}$$، خواهیم داشت:

$${B_{\,n}} = \frac{2}{{{n^2}{\pi ^2}}}\left( { - n\pi L{{\left( { - 1} \right)}^n}} \right) = \frac{{{{\left( { - 1} \right)}^{n + 1}}2L}}{{n\pi }}\hspace{0.25in}\hspace{0.25in}n = 1,2,3 \ldots$$

بنابراین سری فوریه سینوسی به صورت زیر نوشته می‌شود:

$$x = \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}2L}}{{n\pi }}\sin \left( {\frac{{n\,\pi x}}{L}} \right)} = \frac{{2L}}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)}$$

بسط نیم‌دامنه سری فوریه سینوسی

حال فرض کنید بخواهیم سری فوریه سینوسی یک تابع غیرفرد را بیابیم. همانطور که می‌دانیم، سری فوریه فقط برای توابع متناوب تعریف می‌شود، بنابراین در این حالت باید تابع را گسترش دهیم تا به یک تابع متناوب تبدیل شود.

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

تابع $$f(x)$$ روی بازه $$0 \le x \le L$$ تعریف شده است و فرد نیست. این تابع باید به بازه $$- L \le x \le L$$ گسترش یابد تا بتوان برای آن، سری فوریه را نوشت. تعمیم فرد تابع $$f(x)$$ روی بازه $$- L \le x \le L$$ به صورت زیر نوشته می‌شود:

$$ g\left( x \right) = \Bigg \{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{-f\left( { - x} \right)}&{\,\,\,\,{\mbox{if}} - L \le x \le 0}\end{array}} .$$

تابع $$g(x)$$، فرد است. زیرا:

$$g\left( -x \right)=-f\left( -\left( -x \right) \right)=-f\left( x \right)=-g\left( x \right) \hspace{0.25in} \text{for}$$ $$0$$

مشاهده می‌شود که روی بازه $$0 \le x \le L$$ توابع $$g(x)$$ و $$f(x)$$ با هم برابر هستند. اگر $$f(x)$$ یک تابع فرد باشد، $$g(x)$$ و $$f(x)$$ در بازه $$-L \le x \le L$$ برابر هستند.

حال می‌خواهیم دریابیم چگونه می‌توان بر اساس گسترش فرد یک تابع، بسط فوریه هر تابعی را در بازه $$0 \le x \le L$$ یافت.

اگر تابع $$f(x)$$ را در نظر بگیریم، تابع $$g(x)$$ همانند بالا تعریف می‌شود. $$g(x)$$، یک تابع فرد در بازه $$-L \le x \le L$$ است. پس می‌توان سری فوریه سینوسی آن را به صورت زیر نوشت:

$${b_n} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}\,\,\,\,\,\,\,n = 1,2,3, \ldots$$

در بازه $$0 \le x \le L$$، دو تابع $$f(x)$$‌ و $$g(x)$$ با هم برابر هستند. پس سری فوریه سینوسی تابع $$f\left( x \right)$$ روی بازه $$0 \le x \le L$$ به صورت زیر خواهد بود:

$$f\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin \left( {\frac{{n\,\pi x}}{L}} \right)} , \, \, \, \, {b_n} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}\,\,\,\,\,\,\,n = 1,2,3, \ldots$$

در ادامه به بیان چند مثال برای یافتن سری فوریه سینوسی توابع غیرفرد خواهیم پرداخت.

مثال ۲

سری فوریه سینوسی تابع $$f\left( x \right) = L - x$$ را در بازه $$0 \le x \le L$$ بیابید.

حل: ابتدا باید تابع $$f(x)$$ را گسترش داد تا به یک تابع فرد تبدیل شود. سپس سری فوریه برای آن نوشته می‌شود.

گسترش فرد تابع $$f(x)$$‌ به صورت زیر است:

$$\begin{align*}g\left( x \right) & = \Bigg\{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{-f\left( { - x} \right)}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\\ & = \Bigg\{ {\begin{array}{*{20}{l}}{L - x}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{-L - x}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\end{align*}$$

در شکل زیر، تابع مسئله و گسترش فرد آن نشان داده شده است:

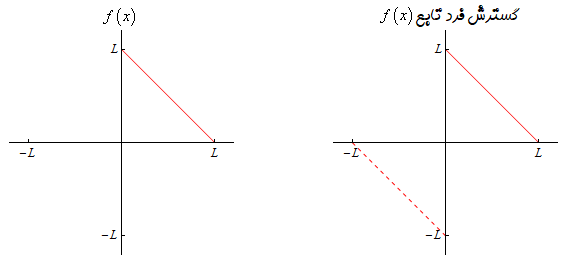
ضرایب سری فوریه سینوسی به صورت زیر هستند:

$$\begin{align*}{b_{\,n}} & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{\left( {L - x} \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\\ & = \frac{2}{L}\left. {\left( { - \frac{L}{{{n^2}{\pi ^2}}}} \right)\left[ {L\sin \left( {\frac{{n\,\pi x}}{L}} \right) - n\pi \left( {x - L} \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \right]} \right|_0^L\\ & = \frac{2}{L}\left[ {\frac{{{L^2}}}{{{n^2}{\pi ^2}}}\left( {n\pi - \sin \left( {n\pi } \right)} \right)} \right] = \frac{{2L}}{{n\pi }}\end{align*}$$

بنابراین سری فوریه تابع $$f(x)$$ عبارت است از:

$$f\left( x \right) = \sum\limits_{n = 1}^\infty {\frac{{2L}}{{n\pi }}\sin \left( {\frac{{n\,\pi x}}{L}} \right)} \,$$

مثال ۳

سری فوریه سینوسی تابع $$f\left( x \right) = {۱+x^2}$$ را در بازه $$0 \le x \le L$$ بیابید.

حل: گسترش فرد این تابع به صورت زیر است:

$$\begin{align*}g\left( x \right) & = \Bigg\{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{ - f\left( { - x} \right)}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\\ & = \Bigg\{ {\begin{array}{*{20}{l}}{1 + {x^2}}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{ - 1 - {x^2}}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\end{align*}$$

در شکل زیر، تابع مسئله و گسترش آن نشان داده شده است:

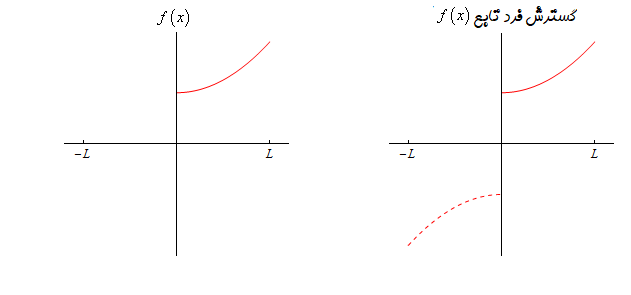
ضرایب سری فوریه سینوسی به صورت زیر هستند:

$$\begin{align*}{b_{\,n}} & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{\left( {1 + {x^2}} \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\\ & = \frac{2}{L}\left( {\frac{L}{{{n^3}{\pi ^3}}}} \right)\left[ {\left( {2{L^2} - {n^2}{\pi ^2}\left( {1 + {x^2}} \right)} \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right) + 2Ln\pi x\sin \left( {\frac{{n\,\pi x}}{L}} \right)} \right]_0^L\\ & = \frac{2}{L}\left( {\frac{L}{{{n^3}{\pi ^3}}}} \right)\left[ {\left( {2{L^2} - {n^2}{\pi ^2}\left( {1 + {L^2}} \right)} \right)\cos \left( {n\pi } \right) + 2{L^2}n\pi \sin \left( {n\pi } \right) - \left( {2{L^2} - {n^2}{\pi ^2}} \right)} \right]\\ & = \frac{2}{{{n^3}{\pi ^3}}}\left[ {\left( {2{L^2} - {n^2}{\pi ^2}\left( {1 + {L^2}} \right)} \right){{\left( { - 1} \right)}^n} - 2{L^2} + {n^2}{\pi ^2}} \right]\end{align*}$$

بنابراین سری فوریه سینوسی تابع $$f(x)$$ به صورت زیر است:

$$f\left( x \right) = \sum\limits_{n = 1}^\infty {\frac{2}{{{n^3}{\pi ^3}}}\left[ {\left( {2{L^2} - {n^2}{\pi ^2}\left( {1 + {L^2}} \right)} \right){{\left( { - 1} \right)}^n} - 2{L^2} + {n^2}{\pi ^2}} \right]\sin \left( {\frac{{n\,\pi x}}{L}} \right)} \,$$

در آموزش بعدی از این سری آموزش‌ها در مجله فرادرس، به بررسی سری فوریه کسینوسی خواهیم پرداخت.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• روش تغییر متغیر برای حل انتگرال — به زبان ساده
• مفاهیم، روش‌ های محاسبه و کاربردهای انتگرال - مجموعه مقالات وبلاگ فرادرس

^^