سری تلسکوپی — به زبان ساده
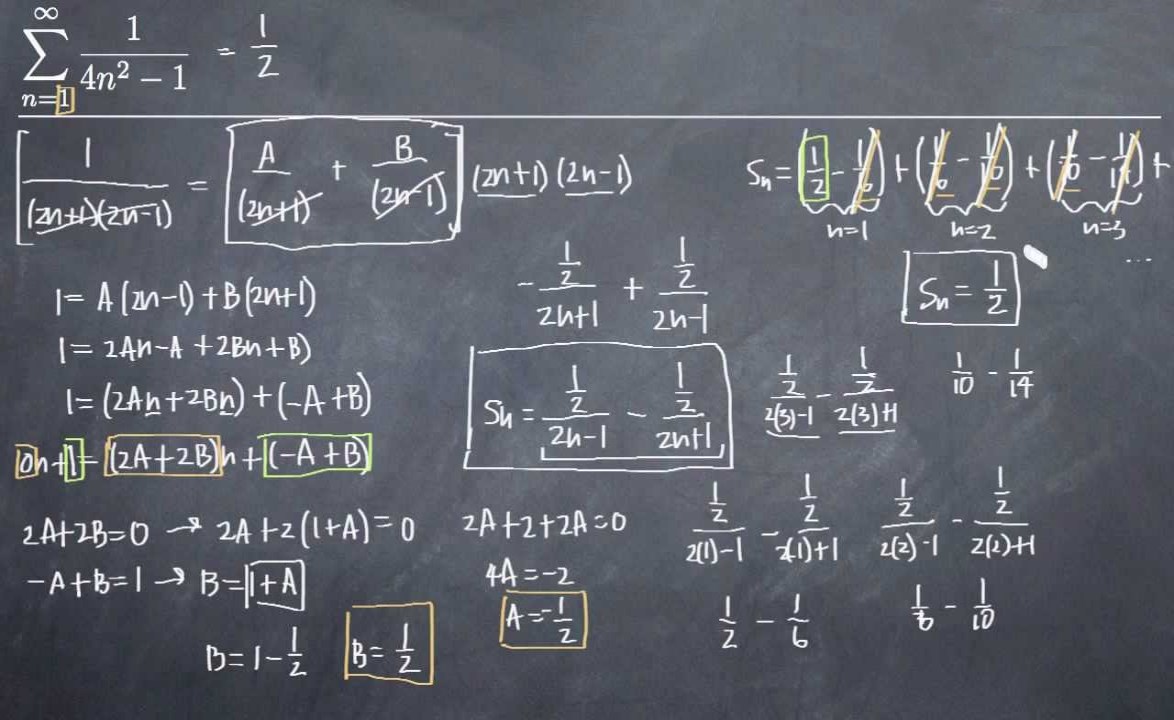
در راستای ارائه مفاهیم مرتبط با سری، در این مطلب میخواهیم تا سری جدیدی تحت عنوان سری تلسکوپی را معرفی کنیم. البته جهت آشنایی بیشتر با مفاهیم سریها مطالعه مطالب سری همگرا و واگرا، آزمون نسبت و سریهای توانی نیز خالی از لطف نخواهند بود.
سری تلسکوپی
در ریاضیات، سری تلسکوپی برابر با حاصل جمعی است که تعداد جملات آنها پس از خنثی کردنشان، عددی محدود است. برای نمونه سری زیر را در نظر بگیرید.
$$ \large \sum _ { { n = 1 } } ^ { \infty } { \frac { 1 } { n ( n + 1 ) } } $$
این سری را میتوان به شکلی نوشت که در آن جملات دو به دو یکدیگر را خنثی کنند. در ادامه سری فوق را بهصورت زیر بازنویسی کردهایم.
$$\begin {align} \sum _ { n = 1 } ^ \infty \frac { 1 } { n ( n + 1 ) } & { } = \sum _ { n = 1 } ^ \infty \left ( \frac { 1 } { n } - \frac { 1 } { n + 1 } \right ) \\ {} & { } = \lim _ { N \to\infty } \sum _ { n = 1 } ^ N \left ( \frac { 1 } { n } - \frac { 1 } { n + 1 } \right ) \\ {} & {} = \lim _ { N \to\infty } \left\lbrack { \left ( 1 - \frac { 1 } { 2 } \right ) + \left(\frac{1}{ 2 } - \frac{1}{3}\right) + \cdots + \left(\frac{1}{N} - \frac{1}{ N + 1} \right ) } \right \rbrack \\ {} & {} = \lim _ { N \to\infty } \left\lbrack { 1 + \left ( - \frac { 1 } { 2 } + \frac { 1 } { 2 } \right ) + \left( - \frac{1}{3} + \frac { 1} { 3 } \right) + \cdots + \left( - \frac { 1 } { N } + \frac { 1 } { N } \right) - \frac{1}{N+1} } \right\rbrack \\ { } & { } = \lim _ { N \to\infty } \left\lbrack { 1 - \frac{1}{N+1} } \right\rbrack = 1 \end{align} $$
همانطور که مشاهده میشود در عبارت فوق، کسرها، دو به دو یکدیگر را خنثی کرده تا اینکه نهایتا جملات اول (که برابر با $$1$$ است) و آخر یا همان $$ \frac { 1 } { N + 1 } $$ باقی میمانند. در این موارد میتوان مقدار سری را با استفاده از حد و به راحتی محاسبه کرد. توجه داشته باشید که همواره میتوان با استفاده از نوشتن سری تلسکوپی به صورتی که جملات آن یکدیگر را خنثی کنند، وضعیت همگرایی آن را تعیین کرد. این روش تحت عنوان قاعده ادغام شناخته میشود. در حقیقت فرض کنید $$ a _ n $$ نشاندهنده جملات عمومی یک سری بوده و حاصل حد آنها در بینهایت برابر با صفر باشد. حال میخواهیم حاصل جمع جملات این سری را بدست آوریم. با جمع زدن جملات سری داریم:
$$ \large \sum _ { { n = 1 } } ^ { N } \left ( a _{ n } - a _ { { n -1 } } \right ) = a _ { N } - a _ { { 0 } } $$
با توجه به صفر بودن حد آن در بینهایت، حاصل سری فوق برابر میشود با:
$$ \large \sum _ { { n = 1 } } ^ { \infty } \left ( a_ { n } - a _ { { n -1 } } \right ) = - a _ { { 0 } } $$
در ادامه چندین مثال در مورد استفاده از این قاعده را ارائه خواهیم کرد که بهمنظور درک بهتر پیشنهاد میشود آنها را مطالعه فرمایید.
مثال ۱
وضعیت همگرایی سری زیر به چه صورت است؟
$$ \large \sum \limits _ { n = 0 } ^ \infty { \frac { 1 } { { { n ^ 2 } + 3 n + 2 } } } $$
در ابتدا باید جمع جزئی سری فوق را بهصورت زیر بیان کرد:
$$ \large { s _ n } = \sum \limits _ { i = 0 } ^ n { \frac { 1} { { { i ^ 2 } + 3 i + 2 } } } $$
حال میتوان جمع جزئی فوق را نیز بهشکل زیر بیان کرد:
$$ \large \frac { 1 } { { { i ^ 2 } + 3 i + 2 } } = \frac { 1 } { { \left ( { i + 2 } \right ) \left ( { i + 1 } \right ) } } = \frac { 1 } { { i + 1 } } - \frac { 1 } { { i + 2 } } $$
عبارت فوق به نحوی بیان شده که جملات آن یکدیگر را خنثی میکنند. در ادامه این امر نشان داده شده است.
$$ \large \begin {align*} { s _ n } & = \sum \limits _ { i = 0 } ^ n { \left ( { \frac { 1 } { { i + 1 } } - \frac { 1 } { { i + 2 } } } \right ) } \\ & = \left ( { \frac { 1 } { 1 } - \require {cancel} \cancel { { \frac{1}{ 2 } } } } \right) + \left( {\require{cancel} \cancel { { \frac { 1 }{2}}} - \require{cancel} \bcancel { { \frac { 1 } { 3 }} } } \right) + \left( {\require{cancel} \bcancel { { \frac{1 } { 3 } }} - \require{cancel} \cancel{{\frac{1}{4}}}} \right ) + \cdots + \left( {\require{cancel} \cancel{{\frac{1}{n}}} - \require{cancel} \bcancel { { \frac { 1 } { { n + 1 } } } } } \right) + \left( { \require{cancel} \bcancel { { \frac { 1 } { { n + 1 } } } } - \frac{1}{{n + 2 } } } \right ) \\ & = 1 - \frac{1}{{n + 2}}\end{align*}$$
همانطور که میبینید سری فوق بهصورت تلسکوپی بوده و ترم آخر آن نیز در بینهایت به صفر میل میکند. حال کافی است حد فوق را بهصورت زیر محاسبه کنیم.
$$ \large \mathop { \lim } \limits _ { n \to \infty } { s _ n } = \mathop { \lim } \limits _ { n \to \infty } \left ( { 1 - \frac { 1 } { { n + 2 } } } \right ) = 1 $$
در نتیجه سری زیر نیز همگرا است:
$$ \large \sum \limits _ { n = 0 } ^ \infty { \frac { 1 } {{ { n ^2 } + 3 n + 2 } } } = 1 $$
مثال ۲
وضعیت همگرایی سری تلسکوپی زیر را مشخص کرده و در صورت همگرا بودن حاصل جمع جملات آن را بدست آورید.
$$ \large \sum _ { n = 1 } ^ { \infty } \frac { 1 } { ( 2 n - 1 ) ( 2 n + 1 ) } $$
با بازکردن این سری داریم:
$$ \large \begin {align} \quad \sum _ { n = 1 } ^ { \infty } \frac { 1 } { ( 2 n - 1) ( 2 n + 1 ) } = \frac { 1 } { 1 \times 3 } + \frac { 1 } { 3 \times 5} + \frac { 1 } { 5 \times 7 } + ... \end {align} $$
در این مثال قصد داریم تا با استفاده از روش تجزیه کسرها، سری را به صورت تلسکوپی بیان کنیم. بنابراین با توجه به اینکه مخرج کسر از حاصلضرب دو جمله تشکیل شده، لذا میتوان آن را با استفاده از دو ثابت بهصورت زیر در نظر گرفت.
$$ \large \begin {align} \frac { 1 } { ( 2 n - 1 ) ( 2 n + 1 ) } = \frac { A } { ( 2 n - 1 ) } + \frac { B } { ( 2 n + 1 ) } = \frac { A ( 2 n + 1 ) + B ( 2 n - 1 ) } { ( 2 n- 1 ) ( 2 n + 1 ) } \end {align} $$
بنابراین میتوان یکی از معادلات به منظور یافتن ضرایبِ $$ A , B $$ مطابق با معادله زیر بدست میآید.
$$ \large 1 = A ( 2 n + 1 ) + B ( 2 n - 1 ) $$
معادله فوق به ازای تمامی مقادیر $$ n \in \mathbb { R } $$ برقرار است. در حقیقت این رابطه نباید وابسته به مقدار $$ n $$ باشد. بدین منظور مقادیر $$ A , B $$ باید عکس یکدیگر باشند. بنابراین با حذف ترمهای شاملِ $$ n $$، دیگر عبارات مقدار $$ 1 $$ را نتیجه میدهند. لذا با حل دستگاه معادلات زیر، مقادیر $$ B , A $$ بدست میآیند.
$$ \large {\begin {cases} 2 n ( A + B )=0 \\ A - B = 1 & \end {cases} } \Rightarrow A=\frac {1}{2} \ , \ B = - \frac { 1 } { 2 } $$
با جایگذاری مقادیر بدست آمده در عبارت در نظر گرفته شده، کسر به صورت زیر تجزیه میشود:
$$ \large \begin {align} \frac { 1 } { ( 2 n - 1 ) ( 2 n + 1 ) } = \frac { 1 } { 4 n - 2 } -\frac { 1 } { 4 n + 2 } \end{align}$$
در نتیجه سری را نیز میتوان بهشکل زیر بازنویسی کرد:
$$ \large \begin {align} \quad \sum _ { n = 1 } ^ { \infty } \frac { 1} { ( 2 n - 1 ) ( 2 n + 1 ) } = \sum _ { n = 1 } ^ { \infty } \left ( \frac { 1 } { 4 n - 2 } -\frac { 1 } { 4 n + 2 } \right ) \end {align} $$
جملات سری فوق دو به دو یکدیگر را خنثی میکنند؛ به منظور تشخیص جملات باقیمانده بهتر است، سری را به صورت زیر باز کرده، در نتیجه حاصل جمع $$ s _ n $$ نیز بدست خواهد آمد.
$$ \large \begin {align} \quad \quad s_n = \sum_{i=1}^{n} \left ( \frac { 1 } { 4 i - 2 } -\frac { 1 } { 4 i + 2 } \right ) = \left ( \frac{1}{2} -\frac{1}{6} \right) + \left ( \frac { 1 } { 6 } - \frac { 1 } { 1 0 } \right ) + \left ( \frac{1}{10} -\frac{1}{14} \right) + ... + \left ( \frac { 1 } { 4 n - 2 } -\frac { 1 } { 4 n + 2 } \right ) \\ \quad s_n = \frac { 1 } { 2 } - \frac { 1 } { 4 n + 2 } \end{align} $$
با محاسبه حاصل جمعِ $$ s _ n $$ در بینهایت، داریم:
$$ \large \begin {align} \lim_{n \to \infty } s _ n = \lim _ { n \to \infty } \left ( \frac { 1 } { 2 } - \frac { 1 } { 4 n + 2 } \right ) = \frac { 1 } { 2 } \end {align} $$
بنابراین سری به عدد $$\frac { 1 } { 2 } $$ همگرا است.
مثال ۳
وضعیت همگرایی سری تلسکوپی $$ \sum _ { n = 1 } ^ { \infty } \frac { 3 } { n ^ 2 + 3 n + 2 } $$ را تعیین کنید.
با توجه به اینکه عبارت فوق یک سری تلسکوپی محسوب میشود بنابراین مشابه با مثال قبل، در ابتدا باید مخرج سری را به صورت حاصلضرب چند عبارت بیان کرد. از این رو در اولین قدم، این کسر را به صورت زیر بازنویسی میکنیم.
$$ \large a _ n = \frac { 3 } { ( n + 1 ) ( n + 2 ) } $$
بنابراین شکل جزئی کسر نیز به صورت زیر قابل بازنویسی است.
$$ \large \begin {align} \frac { 3 } { ( n + 1 ) ( n + 2 ) } = \frac { A } { ( n + 1 ) } + \frac { B } { ( n + 2 ) } = \frac { A ( n + 2 ) + B ( n + 1 ) }{ (n + 1 ) ( n + 2 ) } \end{align}$$
بدیهی است که حاصل جمع ترمهای قرار گرفته در صورت باید برابر با $$ 3 $$ باشد. همچنین عبارت نباید وابسته به مقدار $$ n $$ باشد. بنابراین دو معادله زیر به منظور بدست آوردن $$ A , B $$ قابل بیان است.
$$\large A + B = 0 $$
$$ \large 2 A + B = 3 $$
با حل دو معادله فوق، مقادیر $$ A $$ و $$ B $$ برابر میشوند با:
$$ \large A = 3 , B = - 3 $$
در نتیجه کسر را میتوان به شکل زیر بازنویسی کرد:
$$ \large \begin {align} \frac { 3 } { ( n + 1 ) ( n + 2 ) } = \frac { 3 } { ( n + 1 ) } - \frac { 3 } { ( n + 2 ) } \end {align} $$
بنابراین سری نیز به شکل زیر قابل بازنویسی است.
$$ \large \begin {align} \quad \sum _ { n = 1 } ^ { \infty } \frac { 1 } { n ^ 2 + 3 n + 2 } = \sum _ { n = 1 } ^ { \infty } \left ( \frac { 3 } { ( n + 1 ) } - \frac { 3 }{ ( n + 2 ) } \right ) \end {align} $$
حال جمع جزئی $$ n $$ جمله اول برابر میشود با:
$$ \large \begin{align} \quad \quad s_n = \sum_{i=1}^{n} \left ( \frac { 3 } { ( i + 1 ) } - \frac { 3 } { ( i + 2 ) } \right ) = \left ( \frac { 3} { 2 } - \frac { 3 } { 3 } \right ) + \left ( \frac { 3 } { 3 } - \frac { 3 } { 4 } \right ) + \left ( \frac { 3 } { 4 } - \frac { 3 } { 5 } \right ) + ... + \left ( \frac { 3 } { n + 1 } - \frac { 3 } { n + 2 } \right ) \end {align} $$
$$\large \Rightarrow s _ n = \frac { 3 } { 2 } - \frac { 3 } { n + 2 }$$
بنابراین حاصل جمع جزئی سری برابر با حد زیر بدست میآید.
$$ \large \begin{align} \quad \lim_{n \to \infty } s _ n = \lim _ { n \to \infty } \left ( \frac { 3 } { 2 } - \frac { 3 } { n + 2 } \right ) = \frac { 3 } { 2 } \end {align} $$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^











توضیحاتشون خیلییی خوب بود
سپاسگزارم
سلام بسیارزیبا ومختصر بود سپاس