در آموزشهای پیشین مجله فرادرس ، با برخی از روشهای درونیابی، از قبیل درونیابی چندجملهای ، لاگرانژ ، هرمیت و اسپلاین آشنا شدیم. در این آموزش، درون یابی خطی را معرفی خواهیم کرد.
«تابع درونیابی» (Interpolation Function) تابعی است که دقیقاً از یک مجموعه نقطه داده عبور میکند. توابع درونیاب دادههای جدولی به فرم زیر را درونیابی میکنند.
x sin ( x ) 0.0 0.000000 0.5 0.479426 1.0 0.841471 1.5 0.997495 2.0 0.909297 2.5 0.598472 \begin {array} { | c | c | } \hline x & { \sin ( x ) } \\ \hline 0 . 0 & { 0 . 0 0 0 0 0 0 } \\ \hline 0 . 5 & { 0 . 4 7 9 4 2 6 } \\ \hline 1 . 0 & { 0 . 8 4 1 4 7 1 } \\ \hline 1 . 5 & { 0 . 9 9 7 4 9 5 } \\ \hline 2 . 0 & { 0 . 9 0 9 2 9 7 } \\ \hline 2 . 5 & { 0 . 5 9 8 4 7 2 } \\ \hline \end {array} x 0.0 0.5 1.0 1.5 2.0 2.5 sin ( x ) 0.000000 0.479426 0.841471 0.997495 0.909297 0.598472
در جدول دادهها، تابع تنها در تعداد محدودی نقطه یا مجموعه گسستهای از مقادیر متغیر مستقل مشخص شده است. میتوان از درونیابی برای یافتن مقادیر تابعی در سایر مقادیر متغیرهای مستقل، مثلاً sin ( 0.63253 ) \sin (0.63253) sin ( 0.63253 ) انتگرالگیری عددی ، مشتقگیری عددی و روش اجزای محدود استفاده میکنیم.
از درونیابی معمولاً برای به دست آوردن یک توصیف تابعی از دادههای اندازهگیری شده استفاده نمیشود، زیرا خطاهای دادهها ممکن است منجر به یک نمایش ضعیف از تابع شود.
درون یابی خطی
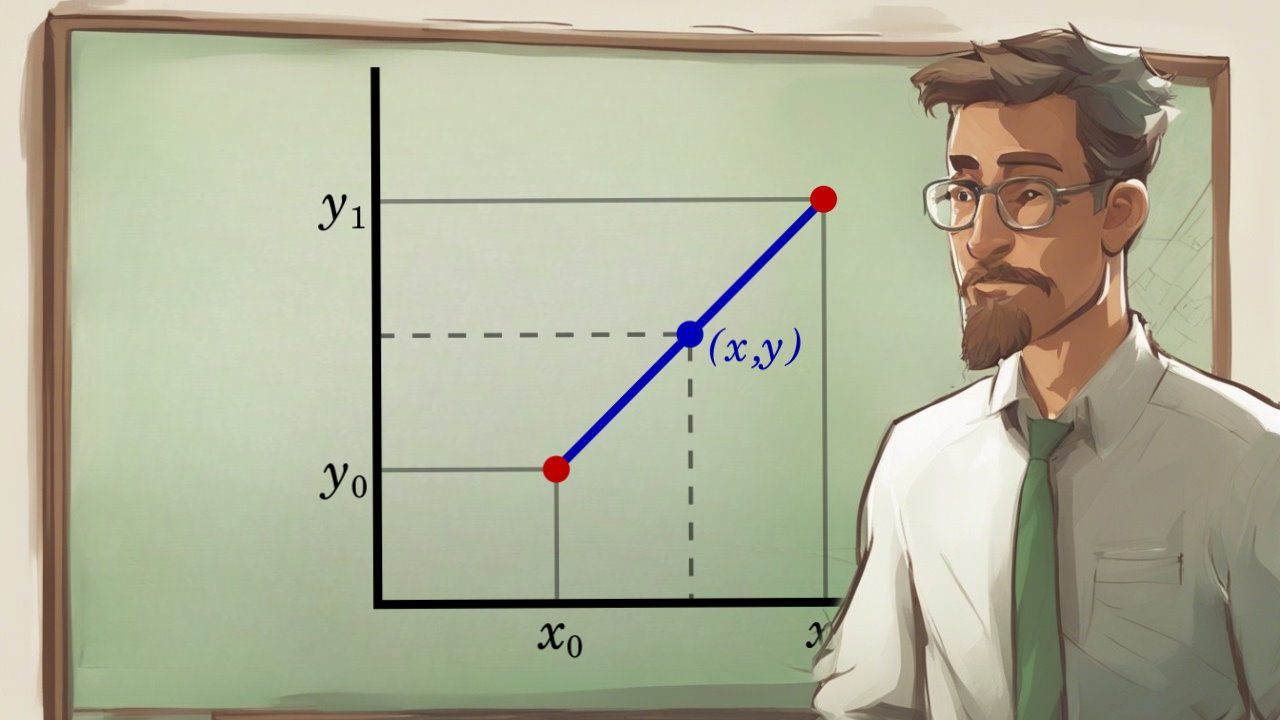
به طور ساده، میتوان گفت که «درون یابی خطی» (Linear Interpolation) عبور دادن یک خط راست بین دو نقطه داده است.
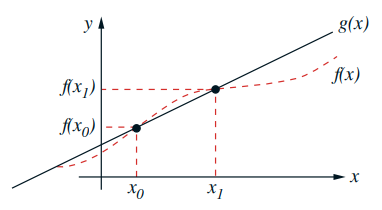
در شکل بالا، f ( x ) f ( x) f ( x ) g ( x ) g ( x ) g ( x ) f ( x ) f ( x ) f ( x ) x 0 x _ 0 x 0 x 1 x _ 1 x 1
به عبارت دیگر، به فرم جدولی میتوانیم بنویسم:
x o f ( x o ) x g ( x ) x 1 f ( x 1 ) \begin {array} { l l } { x _ { o } } & { f \left ( x _ { o } \right ) } \\ { x } & { g ( x ) } \\ { x _ { 1 } } & { f \left ( x _ { 1 } \right ) } \end {array} x o x x 1 f ( x o ) g ( x ) f ( x 1 )
اگر g ( x ) g ( x ) g ( x )
g ( x ) = A x + B ( 1 ) g ( x ) = A x + B \;\;\;\;\; ( 1 ) g ( x ) = A x + B ( 1 )
برای عبور دادن خط از نقاط ( x 0 , f ( x 0 ) ) ( x _ 0 , f ( x _ 0 )) ( x 0 , f ( x 0 )) ( x 1 , f ( x 1 ) ) ( x _ 1 , f (x _ 1 )) ( x 1 , f ( x 1 ))
g ( x 0 ) = f ( x 0 ) ⇒ A x 0 + B = f ( x 0 ) ( 2 ) g ( x 1 ) = f ( x 1 ) ⇒ A x 1 + B = f ( x 1 ) ( 3 ) \begin {array} { l } { g \left ( x _ { 0 } \right ) = f \left ( x _ { 0 } \right ) \quad \Rightarrow \quad A x _ { 0 } + B = f \left ( x _ { 0 } \right ) }\;\;\;\;\; ( 2) \\ { g \left ( x _ { 1 } \right ) = f \left ( x _ { 1 } \right ) \quad \Rightarrow \quad A x _ { 1 } + B = f \left ( x _ { 1 } \right ) }\;\;\;\;\; ( 3 ) \end {array} g ( x 0 ) = f ( x 0 ) ⇒ A x 0 + B = f ( x 0 ) ( 2 ) g ( x 1 ) = f ( x 1 ) ⇒ A x 1 + B = f ( x 1 ) ( 3 )
همانطور که میبینیم، یک دستگاه معادلات خطی با دو معادله و دو مجهول داریم. حال باید A A A B B B
با استفاده از معادله (۲)، میتوان نوشت:
B = f ( x 0 ) − A x 0 B = f ( x _ 0 ) - A x _ 0 B = f ( x 0 ) − A x 0
با جایگذاری این عبارت در (۳)، خواهیم داشت:
A x 1 + f ( x 0 ) − A x 0 = f ( x 1 ) A x _ 1 + f ( x _ 0 ) - A x _ 0 = f ( x _ 1 ) A x 1 + f ( x 0 ) − A x 0 = f ( x 1 )
A = f ( x 1 ) − f ( x 0 ) x 1 − x B = f ( x 0 ) x 1 − f ( x 1 ) x 0 x 1 − x 0 \begin {aligned} & A = \frac { f \left ( x _ { 1 } \right ) - f \left ( x _ { 0 } \right ) } { x _ { 1 } - x _ { } } \\ & B = \frac { f \left ( x _ { 0 } \right ) x _ { 1 } - f \left ( x _ { 1 } \right ) x _ { 0 } } { x _ { 1 } - x _ { 0 } } \end {aligned} A = x 1 − x f ( x 1 ) − f ( x 0 ) B = x 1 − x 0 f ( x 0 ) x 1 − f ( x 1 ) x 0
حال که A A A B B B
g ( x ) = f ( x 0 ) ( x 1 − x ) ( x 1 − x 0 ) + f ( x 1 ) ( x − x 0 ) ( x 1 − x 0 ) \boxed { g ( x ) = f \left ( x _ { 0 } \right ) \frac { \left ( x _ { 1 } - x \right ) } { \left ( x _ { 1 } -x _ { 0 } \right ) } + f \left ( x _ { 1 } \right ) \frac { \left ( x - x _ { 0 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } } g ( x ) = f ( x 0 ) ( x 1 − x 0 ) ( x 1 − x ) + f ( x 1 ) ( x 1 − x 0 ) ( x − x 0 )
این همان فرمول درون یابی خطی است.
مثال ۱
مقادیر x 0 x _ 0 x 0 x 1 x _ 1 x 1 f ( x 0 ) f ( x _ 0 ) f ( x 0 ) f ( x 1 ) f ( x _ 1 ) f ( x 1 ) g ( 0.632 ) g(0. 632) g ( 0.632 )
x f ( x ) = sin x x 0 = 0.5 f ( x 0 ) = 0.47942554 0.632 g ( 0.632 ) = ? x 1 = 1.0 f ( x 1 ) = 0.84147099 \begin {array} { | c | c | } \hline x & { f ( x ) = \sin x } \\ \hline x _ { 0 } = 0 .5 & { f \left ( x _ { 0 } \right ) = 0 . 4 7 9 4 2 5 5 4 } \\ \hline 0 . 6 3 2 & { g ( 0 . 6 3 2 ) = ? } \\ \hline x _ { 1 = 1 . 0 } & { f \left ( x _ { 1 } \right ) = 0 . 8 4 1 4 7 0 9 9 } \\ \hline \end {array} x x 0 = 0.5 0.632 x 1 = 1.0 f ( x ) = sin x f ( x 0 ) = 0.47942554 g ( 0.632 ) = ? f ( x 1 ) = 0.84147099
با استفاده از فرمول درون یابی خطی که به دست آوردیم، داریم:
g ( 0.632 ) = 0.479425 ( 1.0 − 0.632 ) ( 1.0 − 0.5 ) + 0.84147099 ( 0.632 − 0.5 ) ( 1.0 − 0.5 ) g ( 0 . 6 3 2 ) = 0 . 4 7 9 4 2 5 \frac { ( 1 . 0 - 0 . 6 3 2 ) } { ( 1. 0- 0 . 5 ) }+ 0 . 8 4 1 47 0 9 9 \frac { ( 0 .6 3 2 - 0 . 5 ) }{ ( 1 . 0- 0 . 5 ) } g ( 0.632 ) = 0.479425 ( 1.0 − 0.5 ) ( 1.0 − 0.632 ) + 0.84147099 ( 1.0 − 0.5 ) ( 0.632 − 0.5 )
بنابراین، g ( 0.632 ) = 0.57500 g ( 0. 6 3 2 ) = 0.57500 g ( 0.632 ) = 0.57500
خطای درون یابی خطی
خطای درون یابی خطی به صورت زیر تعریف میشود:
e ( x ) ≡ f ( x ) − g ( x ) e ( x ) \equiv f ( x ) - g ( x ) e ( x ) ≡ f ( x ) − g ( x )
که اختلاف بین تابع دقیق f ( x ) f ( x ) f ( x ) g ( x ) g ( x ) g ( x ) x 0 x _ 0 x 0 x 1 x _ 1 x 1 e ( x 0 ) = 0 e ( x _ 0 ) = 0 e ( x 0 ) = 0 e ( x 1 ) = 0 e ( x _ 1 ) = 0 e ( x 1 ) = 0 g ( x 0 ) = f ( x 0 ) g ( x _ 0 ) = f ( x _ 0 ) g ( x 0 ) = f ( x 0 ) g ( x 1 ) = f ( x 1 ) g ( x _ 1 ) = f ( x _ 1 ) g ( x 1 ) = f ( x 1 )
محاسبه e ( x ) \large e ( x ) e ( x )
خطای e ( x ) e ( x ) e ( x )
گام ۱: بسط سری تیلور f ( x ) f ( x ) f ( x ) x 0 x _ 0 x 0
f ( x ) = f ( x 0 ) + ( x − x 0 ) d f d x ∣ x = x 0 + ( x − x 0 ) 2 2 ! d 2 f d x 2 ∣ x = ξ , x 0 ≤ ξ ≤ x ( 4 ) f ( x ) = f \left ( x _ { 0 } \right ) + \left.\left ( x - x _ {0 } \right ) \frac { d f } { d x } \right | _ { x = x _ { 0 } } + \left. \frac { \left ( x - x _ { 0 } \right ) ^ { 2 } } { 2 ! } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \quad \text {, } x _ { 0 } \leq \xi \leq x \;\;\;\;\; ( 4 ) f ( x ) = f ( x 0 ) + ( x − x 0 ) d x df x = x 0 + 2 ! ( x − x 0 ) 2 d x 2 d 2 f x = ξ , x 0 ≤ ξ ≤ x ( 4 )
جمله سوم، باقیمانده واقعی است و همه جملات دیگر در سری را نشان میدهد، زیرا در x = ξ x = \xi x = ξ
گام ۲: عبارت d f d x ∣ x = x 0 \left.\frac { d f } { d x } \right | _ { x = x _ { 0 } } d x df x = x 0 f ( x 0 ) f ( x _ 0 ) f ( x 0 ) f ( x 1 ) f ( x _ 1 ) f ( x 1 ) x = x 1 x = x _ 1 x = x 1
f ( x 1 ) = f ( x 0 ) + ( x 1 − x 0 ) d f d x ∣ x = x 0 + ( x 1 − x 0 ) 2 2 ! d 2 f d x 2 ∣ x = ξ ( 5 ) f \left ( x _ { 1 } \right ) = f \left ( x _ { 0 } \right ) + \left . \left ( x _ { 1 } - x _ { 0 } \right ) \frac { d f } { d x } \right | _ { x = x _ { 0 } } + \left . \frac { \left ( x_ { 1 } - x _ { 0 } \right ) ^ { 2 } } { 2 ! } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; (5) f ( x 1 ) = f ( x 0 ) + ( x 1 − x 0 ) d x df x = x 0 + 2 ! ( x 1 − x 0 ) 2 d x 2 d 2 f x = ξ ( 5 )
بنابراین، داریم:
d f d x ∣ x = x 0 = f ( x 1 ) ( x 1 − x 0 ) − f ( x 0 ) ( x 1 − x 0 ) − ( x 1 − x 0 ) 2 2 ! ⋅ 1 ( x 1 − x 0 ) d 2 f d x 2 ∣ x = ξ ( 6 ) \left . \frac { d f } { d x } \right | _ { x = x _ { 0 } } = \frac { f \left ( x _ { 1 } \right ) } { \left ( x _{ 1 } -x _ { 0 } \right ) } - \frac { f \left ( x _ { 0 } \right ) } { \left ( x _ { 1 } -x _ { 0 } \right ) } - \left . \frac { \left ( x _ { 1 } -x _ { 0 } \right ) ^ { 2 } } { 2 ! } \cdot \frac { 1 } { \left ( x _ { 1 } - x _ { 0 } \right ) } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; ( 6 ) d x df x = x 0 = ( x 1 − x 0 ) f ( x 1 ) − ( x 1 − x 0 ) f ( x 0 ) − 2 ! ( x 1 − x 0 ) 2 ⋅ ( x 1 − x 0 ) 1 d x 2 d 2 f x = ξ ( 6 )
و در نتیجه:
d f d x ∣ x = x 0 = f ( x 1 ) ( x 1 − x 0 ) − f ( x 0 ) ( x 1 − x 0 ) − ( x 1 − x 0 ) 2 d 2 f d x 2 ∣ x = ξ ( 7 ) \left . \frac { d f } { d x } \right | _ { x = x _ { 0 } } = \frac { f \left ( x _ { 1 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } - \frac { f \left ( x _ { 0 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } - \left . \frac { \left ( x _ { 1 } - x _ { 0 } \right ) } { 2 } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; ( 7 ) d x df x = x 0 = ( x 1 − x 0 ) f ( x 1 ) − ( x 1 − x 0 ) f ( x 0 ) − 2 ( x 1 − x 0 ) d x 2 d 2 f x = ξ ( 7 )
فرمول اخیر یک تقریب گسسته برای مشتق اول است.
گام ۳: معادله (۷) را در فرم (۴) سری تیلور f ( x ) f ( x ) f ( x ) f ( x ) f ( x ) f ( x ) f ( x 0 ) f ( x _ 0 ) f ( x 0 ) f ( x 1 ) f ( x _ 1 ) f ( x 1 )
f ( x ) = f ( x 0 ) + ( x − x 0 ) [ f ( x 1 ) ( x 1 − x 0 ) − f ( x 0 ) ( x 1 − x 0 ) − ( x 1 − x 0 ) 2 d 2 f d x 2 ∣ x = ξ ] + ( x − x 0 ) 2 2 d 2 f d x 2 ∣ x = ξ ( 8 ) f ( x ) = f \left ( x _ { 0 } \right ) + \left ( x - x _ { 0 } \right ) \left[ \frac { f \left ( x _ { 1 } \right ) } { \left ( x _ { 1 } -x _ { 0 } \right ) } - \frac { f \left ( x _ { 0 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } -\left. \frac { \left ( x _ { 1 } -x _ { 0 } \right ) } { 2 } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \right ] + \left. \frac { \left ( x - x _ { 0 } \right ) ^ { 2 } } { 2 } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; ( 8 ) f ( x ) = f ( x 0 ) + ( x − x 0 ) [ ( x 1 − x 0 ) f ( x 1 ) − ( x 1 − x 0 ) f ( x 0 ) − 2 ( x 1 − x 0 ) d x 2 d 2 f x = ξ ] + 2 ( x − x 0 ) 2 d x 2 d 2 f x = ξ ( 8 )
در نتیجه:
f ( x ) = f ( x 0 ) + ( x − x 0 ) ( x 1 − x 0 ) f ( x 1 ) − ( x − x 0 ) ( x 1 − x 0 ) f ( x 0 ) + [ ( x − x 0 ) ( − x 1 + x 0 ) 2 + ( x − x 0 ) 2 2 ] d 2 f d x 2 ∣ x = ξ ( 9 ) f ( x ) = f \left ( x _ { 0 } \right ) + \frac { \left ( x -x _ { 0 } \right ) } { \left ( x_ { 1 } - x _ { 0 } \right ) } f \left ( x _ { 1 } \right ) - \frac { \left ( x - x _ { 0 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } f \left ( x _ { 0 } \right ) + \left . \left [ \frac { \left ( x - x _ { 0 } \right ) \left ( - x _ { 1 } + x _ { 0 } \right ) } { 2 } + \frac { \left ( x - x _ { 0 } \right ) ^ { 2 } } { 2 } \right ] \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; (9) f ( x ) = f ( x 0 ) + ( x 1 − x 0 ) ( x − x 0 ) f ( x 1 ) − ( x 1 − x 0 ) ( x − x 0 ) f ( x 0 ) + [ 2 ( x − x 0 ) ( − x 1 + x 0 ) + 2 ( x − x 0 ) 2 ] d x 2 d 2 f x = ξ ( 9 )
بنابراین:
f ( x ) = ( x 1 − x 0 − x + x 0 ) f ( x 0 ) ( x 1 − x 0 ) + ( x − x 0 ) f ( x 1 ) ( x 1 − x 0 ) + ( − x 1 + x 0 + x − x 0 ) ( x − x 0 ) 2 d 2 f d x 2 ∣ x = ξ ( 10 ) f ( x ) = \left ( x _ { 1 } - x _ { 0 } - x + x _ { 0 } \right ) \frac { f \left ( x _ { 0 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } + \left ( x - x _ { 0 } \right ) \frac { f \left ( x _ { 1 } \right ) } { \left ( x _ { 1 } - x _ { 0 } \right ) } + \left . \left ( - x _ { 1 } + x _ { 0 } + x - x _ { 0 } \right ) \frac { \left ( x - x _ { 0 } \right ) } { 2 } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; ( 10 ) f ( x ) = ( x 1 − x 0 − x + x 0 ) ( x 1 − x 0 ) f ( x 0 ) + ( x − x 0 ) ( x 1 − x 0 ) f ( x 1 ) + ( − x 1 + x 0 + x − x 0 ) 2 ( x − x 0 ) d x 2 d 2 f x = ξ ( 10 )
و در نهایت، داریم:
f ( x ) = f ( x 0 ) [ x 1 − x x 1 − x 0 ] + f ( x 1 ) [ x − x 0 x 1 − x 0 ] + ( x − x 0 ) ( x − x 1 ) 2 d 2 f d x 2 ∣ x = ξ ( 11 ) f ( x ) = f \left ( x _ { 0 } \right ) \left [ \frac { x _ { 1 } - x } { x _ { 1 } - x _ { 0 } } \right ] + f \left ( x _ { 1 } \right ) \left [ \frac { x - x _ { 0 } } { x _ { 1 } - x _ { 0 } } \right ] + \left . \frac { \left ( x - x _ { 0 } \right ) \left ( x - x _ { 1 } \right ) } { 2 } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \;\;\;\;\; ( 11 ) f ( x ) = f ( x 0 ) [ x 1 − x 0 x 1 − x ] + f ( x 1 ) [ x 1 − x 0 x − x 0 ] + 2 ( x − x 0 ) ( x − x 1 ) d x 2 d 2 f x = ξ ( 11 )
دو بخش اول رابطه (۱۱) همان فرمول درون یابی خطی است و بخش دیگر نیز در واقع خطا را نشان میدهد. بنابراین:
e ( x ) ≡ f ( x ) − g ( x ) e ( x ) = f ( x 0 ) [ x 1 − x x 1 − x 0 ] + f ( x 1 ) [ x − x 0 x 1 − x 0 ] + ( x − x 0 ) ( x − x 1 ) 2 d 2 f d x 2 ∣ x = ξ − f ( x 0 ) [ x 1 − x x 1 − x 0 ] − f ( x 1 ) [ x − x 0 x 1 − x 0 ] \begin {aligned} e ( x ) & \equiv f ( x ) - g ( x ) \\ e ( x ) & = f \left ( x _ { 0 } \right ) \left [ \frac { x _ { 1 } - x } { x _ { 1 } - x _ { 0 } } \right ] + f \left ( x _ { 1 } \right ) \left [ \frac { x - x _ { 0 } } { x _ { 1 } -x _ { 0 } } \right ] + \left . \frac { \left ( x - x _ { 0 } \right ) \left ( x -x _ { 1 } \right ) } { 2 } \frac { d ^{ 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } - f \left ( x _ { 0 } \right ) \left [ \frac { x _ { 1} - x } { x_ { 1 } - x _ { 0 } } \right ] - f \left ( x _ { 1 } \right ) \left [ \frac { x - x _ { 0 } } { x _ { 1 } - x _ { 0 } } \right ] \end {aligned} e ( x ) e ( x ) ≡ f ( x ) − g ( x ) = f ( x 0 ) [ x 1 − x 0 x 1 − x ] + f ( x 1 ) [ x 1 − x 0 x − x 0 ] + 2 ( x − x 0 ) ( x − x 1 ) d x 2 d 2 f x = ξ − f ( x 0 ) [ x 1 − x 0 x 1 − x ] − f ( x 1 ) [ x 1 − x 0 x − x 0 ]
در نتیجه:
e ( x ) = ( x − x 0 ) ( x − x 1 ) 2 d 2 f d x 2 ∣ x = ξ x 0 ≤ ξ ≤ x 1 e ( x ) = \left . \frac { \left ( x - x _ { 0 } \right ) \left ( x - x_ { 1 } \right ) } { 2 } \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \quad x _ { 0 } \leq \xi \leq x _ { 1 } e ( x ) = 2 ( x − x 0 ) ( x − x 1 ) d x 2 d 2 f x = ξ x 0 ≤ ξ ≤ x 1
اگر فرض کنیم بازه [ x 0 , x 1 ] [ x _ 0 , x _ 1 ] [ x 0 , x 1 ]
d 2 f d x 2 ∣ x = ξ ≅ d 2 f d x 2 ∣ x = x 0 ≅ d 2 f d x 2 ∣ x = x 1 ≅ d 2 f d x 2 ∣ x = x m , x m ≡ x 0 + x 1 2 \begin {aligned} & \left . \left . \left . \left . \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = \xi } \cong \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = x _ { 0 } } \cong \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = x _ { 1 } } \cong \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = x _ { m } } \text {, } \quad x _ { m } \equiv \frac { x _ { 0 } + x _ { 1 } } { 2 } \end {aligned} d x 2 d 2 f x = ξ ≅ d x 2 d 2 f x = x 0 ≅ d x 2 d 2 f x = x 1 ≅ d x 2 d 2 f x = x m , x m ≡ 2 x 0 + x 1
بنابراین، معمولاً جمله مشتق در عبارت خطا را با استفاده از نقطه میانی در بازه محاسبه میکنیم:
e ( x ) ≅ 1 2 ( x − x 0 ) ( x − x 1 ) d 2 f d x 2 ∣ x = x m \left . e ( x ) \cong \frac { 1 } { 2 } \left ( x -x _ { 0 } \right ) \left ( x - x _ { 1 } \right ) \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = x _ { m } } e ( x ) ≅ 2 1 ( x − x 0 ) ( x − x 1 ) d x 2 d 2 f x = x m
یک مسئله دیگر این است که معمولاً مشتق دوم را در نقطه میانی x m x _ m x m
حداکثر خطا در روش درون یابی خطی در نقطه میانی رخ میدهد ( که در آن، ( x − x 0 ) ( x − x 1 ) ( x - x _ 0 ) ( x - x _ 1 ) ( x − x 0 ) ( x − x 1 )
max ∣ e ( x ) ∣ x 0 < x 1 ≅ 1 2 ( x m − x 0 ) ( x m − x 1 ) d 2 f d x 2 ∣ x = x m \left . \max | e ( x ) | _ { x _ { 0 } < x _ { 1 } } \cong \frac { 1 } { 2 } \left ( x _ { m } - x _ { 0 } \right ) \left ( x _ { m } - x _ { 1 } \right ) \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = x _ {m } } max ∣ e ( x ) ∣ x 0 < x 1 ≅ 2 1 ( x m − x 0 ) ( x m − x 1 ) d x 2 d 2 f x = x m
با تعریف h ≡ x 1 − x 0 h \equiv x _ 1 - x _ 0 h ≡ x 1 − x 0 h 2 = x m − x 0 \frac { h } { 2 } = x _ m - x _ 0 2 h = x m − x 0 h 2 = x 1 − x m \frac { h } { 2 } = x _ 1 - x _ m 2 h = x 1 − x m
max ∣ e ( x ) ∣ x 0 < x < x 1 = h 2 8 d 2 f d x 2 ∣ x m \max | e ( x ) | _ { x _ { 0 } < x < x _ { 1 } } = \left . \frac { h ^ {2 } } { 8 } \frac { d ^ { 2 } f } { d x^ { 2 } } \right | _ { x _ { m } } max ∣ e ( x ) ∣ x 0 < x < x 1 = 8 h 2 d x 2 d 2 f x m
در عبارت خطای درون یابی خطی یک چندجملهای و یک مشتق وجود دارد. حداکثر خطا تقریباً در نقطه میانی بین x 0 x _ 0 x 0 x 1 x _ 1 x 1 h h h f ( 2 ) ( x ) f ^ {(2)} ( x ) f ( 2 ) ( x )
مثال ۲
خطای درون یابی خطی مثال ۱ را محاسبه کنید.
حل: همانطور که دیدم:
g ( 0.632 ) = 0.57500 g ( 0.632 ) = 0.57500 g ( 0.632 ) = 0.57500
خطا به صورت زیر تقریب زده میشود:
e ( x ) ≅ 1 2 ( x − x 0 ) ( x − x 1 ) d 2 f d x 2 ∣ x = x m \left . e ( x ) \cong \frac { 1 } { 2 } \left ( x -x _ { 0 } \right ) \left ( x - x _ { 1 } \right ) \frac { d ^ { 2 } f } { d x ^ { 2 } } \right | _ { x = x _ { m } } e ( x ) ≅ 2 1 ( x − x 0 ) ( x − x 1 ) d x 2 d 2 f x = x m
از آنجا که x = 0.750 x = 0.750 x = 0.750 [ 0.5 , 1.0 ] [ 0.5 , 1.0 ] [ 0.5 , 1.0 ]
e ( 0.632 ) ≅ 1 2 ( 0.632 − 0.5 ) ( 0.632 − 1.0 ) d 2 f d x 2 ∣ x = 0.750 e ( 0.632 ) ≅ − 0.024288 d 2 f d x 2 ∣ x = 0.75 \begin {aligned} & \left . e ( 0 . 6 3 2 ) \cong \frac { 1 } { 2 } ( 0 . 6 3 2- 0. 5 ) (0 . 6 3 2 - 1 . 0 ) \frac { d ^ { 2 } f } { d x ^ {2 } } \right | _ { x = 0 . 7 5 0 } \\ & e ( 0 . 6 3 2 ) \cong - \left . 0 . 0 2 4 2 8 8 \frac { d ^ { 2 } f } { d x^ { 2 } } \right | _ { x = 0 . 7 5 } \end {aligned} e ( 0.632 ) ≅ 2 1 ( 0.632 − 0.5 ) ( 0.632 − 1.0 ) d x 2 d 2 f x = 0.750 e ( 0.632 ) ≅ − 0.024288 d x 2 d 2 f x = 0.75
مقدار d 2 f d x 2 ∣ x = 0.75 \left. \frac { d ^ { 2 } f } { d x^ { 2 } } \right | _ { x = 0 . 7 5 } d x 2 d 2 f x = 0.75
d 2 f d x 2 ∣ x = 0.75 = − sin ( 0.750 ) = − 0.68164 \left. \frac { d ^ { 2 } f } { d x^ { 2 } } \right | _ { x = 0 . 7 5 } = - \sin ( 0.750 ) = - 0.68164 d x 2 d 2 f x = 0.75 = − sin ( 0.750 ) = − 0.68164
اکنون با جایگذاری مقدار d 2 f d x 2 ∣ x = 0.75 \left. \frac { d ^ { 2 } f } { d x^ { 2 } } \right | _ { x = 0 . 7 5 } d x 2 d 2 f x = 0.75
e ( 0.632 ) ≅ ( − 0.024288 ) ( − 0.68164 ) = 0.016555 e( 0 . 6 3 2) \cong ( - 0 . 0 2 42 88 ) ( - 0. 68 1 6 4 ) = 0 . 0 1 6 5 5 5 e ( 0.632 ) ≅ ( − 0.024288 ) ( − 0.68164 ) = 0.016555
حال برای مقایسه، خطای واقعی (تفاضل جواب واقعی و جواب جواب تخمینی) را محاسبه میکنیم:
E ( x ) = sin ( x ) − g ( x ) E ( x ) = \sin ( x ) - g ( x ) E ( x ) = sin ( x ) − g ( x )
E ( 0.632 ) = sin ( 0.632 ) − 0.57500 = 0.01576 E ( 0.632) = \sin ( 0 .632) - 0.57500 = 0.01576 E ( 0.632 ) = sin ( 0.632 ) − 0.57500 = 0.01576
میبینیم که خطای تخمینی e ( x ) e ( x ) e ( x ) E ( x ) E ( x ) E ( x )
درون یابی خطی در متلب
همانطور که گفتیم، فرمول درون یابی خطی به صورت زیر است:
y = y 1 + ( y 2 − y 1 ) ( x − x 1 ) ( x 2 − x 1 ) y = y _ 1 + \frac { ( y _ 2 - y _ 1 ) ( x - x _ 1 ) } { ( x _ 2 - x _1)} y = y 1 + ( x 2 − x 1 ) ( y 2 − y 1 ) ( x − x 1 )
کد متلب این روش را میتوان به سادگی به صورت زیر نوشت:
برای مثال، فرض کنید دو نقطه ( 60 , 15.56 ) ( 60 , 15.56 ) ( 60 , 15.56 ) ( 90 , 32.22 ) (90 , 32.22) ( 90 , 32.22 ) y y y x = 73 x = 73 x = 73
که جواب آن برابر است با:
y = 22.7793

















سلام ،
ببخشید چجوری میشه از نمودار رسم شده مقادیر xو y آن را بدست آورد ؟
)درمورد دستور plot گشتم اما هرکاری میکنم نمی تونه از روی خطوط بدست آمده مقادیر xو y خطوط را بدست بیاورم )
سلام.
میتوانید از راهنمای زبان یا نرمافزاری که استفاده میکنید، کمک بگیرید. برای مثال، در متلب میتوانید از دستورهای زیر استفاده کنید:
h = findobj(gca,'Type','line');x=get(h,'Xdata') ;y=get(h,'Ydata')شاد و پیروز باشید.
عالی