فرادرس
دامنه و برد توابع جبری و گویا — به زبان ساده
در آموزش‌های پیشین مجله فرادرس، با تعریف دامنه و برد تابع آشنا شدیم. در این آموزش، روش محاسبه دامنه و برد توابع جبری و گویا را بیان می‌کنیم.
تعریف دامنه تابع
دامنه تابعی مانند $$f$$ که به صورت عبارتی برحسب متغیر $$x$$ تعریف شده است، برابر است با مجموعه اعداد حقیقی متغیر $$x$$ که به ازای آن‌ها مقدار تابع حقیقی است.
تعریف برد تابع
برد تابع $$f$$ برابر است با مجموعه مقادیری که به ازای قرار دادن مقادیر دامنه در متغیر $$x$$ برای تابع حاصل می‌شود.
تعیین دامنه و برد توابع جبری و گویا
برای به دست آوردن دامنه و برد یک تابع ابتدا باید نوع آن تابع را تشخیص دهیم، زیرا توابع گوناگون از جمله توابع جبری، لگاریتمی، گویا، مثلثاتی و... دامنه و برد متفاوتی دارند. در ادامه این مطلب، به منظور آشنایی با نحوه تعیین دامنه و برد توابع جبری و گویا مثال‌هایی را ارائه خواهیم کرد.
دامنه و برد تعدادی از توابع جبری و گویا به شرح زیر است:
| برد | دامنه | تابع |
| $$[0, +∞)$$ | $$(-∞,+∞)$$ | ($$n$$ زوج و $$a\neq0$$) $$ f ( x ) = ( a x \pm b ) ^n $$ |
| $$(-∞,+∞)$$ | $$(-∞,+∞)$$ | ($$n$$ فرد و $$a\neq0$$) $$ f ( x ) = ( a x \pm b ) ^n $$ |
| $$[0, +∞)$$ | $$(-∞,+∞)$$ | $$ f ( x ) = | a x \pm b | , \; a \neq 0 $$ |
| $$[0, +∞)$$ | $$[ \mp \frac b a , +∞) $$ | ($$n$$ زوج و $$a\neq0$$) $$ f ( x ) = { ( a x \pm b ) } ^{\frac 1n} $$ |
| $$(-∞,+∞)$$ | $$(-∞,+∞)$$ | ($$n$$ فرد و $$a\neq0$$) $$ f ( x ) = { ( a x \pm b ) } ^{\frac 1n} $$ |
| $$ ( - \infty , 0 ) \cup ( 0 , + \infty ) $$ | $$ ( -\infty ,\mp \frac b a ) \cup (\mp \frac b a , + \infty ) $$ | $$ f ( x ) = \frac {1}{(ax±b)},\; a \neq 0 $$ |
مثال های تعیین دامنه و برد توابع جبری و گویا
در این بخش، چند مثال را از تعیین دامنه و برد توابع جبری و گویا بیان می‌کنیم.
مثال اول دامنه و برد توابع جبری و گویا
دامنه تابع $$ f ( x ) = \sqrt { ( 1 - x ) / ( x + 3 ) } $$ را بدست آورید.
حل: برای تعیین دامنه این تابع، باید بازه‌ای را پیدا کنیم که در آن، عبارت زیر رادیکال مثبت باشد. بنابراین، صورت و مخرج هردو باید یا مثبت یا منفی باشند. در این صورت، دو شرط خواهیم داشت (در هر دو مورد $$x+3$$ در مخرج باید مخالف صفر باشد، یعنی $$x≠-3$$):
- $$1-x\ge0 $$ و $$ x+3>0$$. یعنی:
$$x\le 1 , x>-3\Rightarrow x\in ( - 3, 1]$$
- $$1-x\le0 $$ و $$ x+3<0$$. یعنی:
$$x\ge1 , x<-3 $$
که در مورد دوم اشتراکی وجود ندارد.
از این رو، دامنه تابع $$( - 3, 1]$$ خواهد بود.
مثال دوم دامنه و برد توابع جبری و گویا
دامنه تابع $$ f ( x ) = \frac {1}{ ( x ^ 3 + x ^ 2 - 2 x ) } $$ را تعیین کنید.
حل: همانطور که می دانید، اگر مخرج یک تابع کسری صفر شود، مقدار تابع بینهایت (تعریف نشده) خواهد بود. بنابراین، باید $$ x ^ 3 + x ^ 2 - 2 x \neq 0 $$ باشد. برای تعیین دامنه، ابتدا باید $$x$$هایی که مخرج را صفر می‌کنند، به دست آوریم:
$$ \large x ^ 3 + x ^ 2 - 2 x = 0 , \\
\large x ( x ^ 2 + x - 2 ) = 0 , \\
\large x ( x - 1 ) ( x + 2 ) = 0 . $$
در نتیجه
$$ \large x=0, \; x=1,\; x = - 2 $$
بنابراین، دامنه تابع برابر است با
$$ \large ( - ∞ , - 2 ) \cup ( - 2 , 0 ) \cup ( 0 , 1 ) \cup ( 1 , + ∞ ) $$
مثال سوم دامنه و برد توابع جبری و گویا
برد تابع $$ f ( x ) = \sqrt { x ^ 2 + 4 x + 4 } - 6 $$ را بیابید.
حل: عبارت زیر رادیکال، یک اتحاد مربع به صورت $$ x ^ 2 + 4 x + 4 = ( x + 2 ) ^ 2 $$ است. بنابراین، داریم:
$$ \large \sqrt {x ^ 2 + 4 x + 4 } - 6 = \sqrt { ( x + 2 ) ^ 2 } - 6 = | x + 2 | - 6 $$
از آنجا که برد تابع $$|x+2$$، بازه $$[0,+\infty$$ است، با جابه‌جایی نمودار این تابع به اندازه شش واحد به سمت پایین، می‌توانیم برد تابع $$ | x + 2 | - 6 $$ را به دست آوریم. بنابراین، برد تابع $$f(x)$$ برابر است با $$[-6, +∞) $$.
مثال چهارم دامنه و برد توابع جبری و گویا
برد تابع $$ f ( x ) = \frac {1} { x ^ 2 + 4 } $$ را به دست آورید.
حل: همانطور که می‌دانید $$ x ^ 2 \ge 0 $$ است. اگر عدد $$4$$ را به طرفین نامعادله اضافه کنیم، داریم:
$$ \large x ^ 2 + 4 \ge 4 $$
در نتیجه، خواهیم داشت:
$$ \large \frac { 1 } { x ^ 2 + 4 } \le \frac 1 4 \\
\large f ( x ) \le \frac 1 4 $$
توجه داشته باشید که $$ \frac {1} { x ^ 2 + 4 } $$ همواره یک عبارت مثبت است و هیچ‌گاه صفر نمی‌شود، اما هنگامی که $$x$$ افزایش می‌یابد، ممکن است خیلی به صفر نزدیک باشد. بنابراین، برد این تابع برابر با $$ (0, \frac 14 ] $$ خواهد بود.
مثال پنجم دامنه و برد توابع جبری و گویا
برد تابع $$ f ( x ) = \frac {x-1} {x+2} $$ را تعیین کنید.
حل: روش جبری به دست آوردن برد این تابع گویا با مثال‌های قبلی متفاوت است. برای یافتن برد این تابع ابتدا باید معکوس آن را به دست آوریم و سپس، دامنه تابع معکوس را تعیین کنیم. زیرا همانطور که در مبحث تابع معکوس بیان شد، دامنه تابع معکوس برابر با برد تابع اصلی است.
از آنجا که $$f(x)$$ تابعی یک به یک است، معکوس‌پذیر نیز هست.
$$ \large y = \frac {x-1} {x+2} $$
تساوی بالا را برحسب $$y$$ به صورت زیر بازنویسی می‌کنیم:
$$ \large x = \frac {y-1} {y+2} $$
با توجه به رابطه فوق، تابع معکوس را می‌توان به شکل زیر نوشت:
$$ \large f ^ { - 1 } ( x ) = y = \frac { 2 x + 1 }{ 1 - x } $$
بنابراین، دامنه $$f^{-1}$$ و در نتیجه برد تابع $$f$$ برابر با $$ ( - ∞ , 1 ) \cup ( 1 , + ∞ ) $$ است.
مثال ششم دامنه و برد توابع جبری و گویا
برد تابع $$ f ( x ) = \frac { 2 x ^ 2 - 1 } { x + 1 } $$ را به دست آورید.
حل: مانند مثال قبل، ابتدا تابع را به صورت زیر می‌نویسیم:
$$ \large y = \frac { 2 x ^ 2 - 1 } { x + 1 } \Rightarrow 2 x ^ 2 - y x - y - 1 = 0 $$
جواب این معادله به صورت زیر است:
$$ \large x _ { 1 , 2 } = \frac { y ± \sqrt {y^2+8y+8} } {2} $$
جواب‌های فوق در صورتی حقیقی هستند که عبارت زیر رادیکال منفی نباشد. بنابراین، باید نامعادله زیر را حل کنیم:
$$ \large y ^ 2 + 8 y + 8≥ 0 , \\
\large ( y + 4 ) ^ 2 ≥ 8 \\
\large y ≥ 2 \sqrt 2-4, \; y≤-4-2\sqrt 2 $$
در نتیجه، برد تابع برابر است با $$ (-∞, -4-2\sqrt 2] \cup [2\sqrt2-4, +∞) $$.
مثال هفتم دامنه و برد توابع جبری و گویا
برد تابع $$ f ( x ) = - \frac 14 | - 4x + 5 | + \frac 1 2 $$ را بیابید.
حل: همانطور که می‌دانید، خروجی تابع قدر مطلق همواره مقداری مثبت است. بنابراین، واضح است که $$ | - 4 x + 5 | \ge 0 $$. با ضرب $$-\frac 14$$ در طرفین نامعادله داریم:
$$ \large -\frac 14 |-4x+5|≤0 $$
حال $$\frac 12$$ را به طرفین این نامعادله اضافه می‌کنیم:
$$ \large -\frac 14 | - 4 x + 5 | + \frac 1 2 ≤ \frac 1 2 $$
واضح است که برد تابع در محدوده $$ ( - ∞ ,\frac 12 ] $$ قرار می‌گیرد.
مثال هشتم دامنه و برد توابع جبری و گویا
دامنه و برد تابع $$ f ( x ) = \sqrt {x^2-4x+8}$$ را به دست آورید.
حل: دامنه این تابع، برابر با مجموعه‌ای از مقادیر $$x$$ است که در رابطه زیر صدق کنند:
$$ \large x ^ 2 - 4 x + 8 ≥ 0 $$
مقدار دلتای این عبارت برابر با $$ ( - 4) ^ 2 + 4 ( 1 ) ( 8 ) = - 16 $$ است. از آنجا که مقدار دلتا منفی است، عبارت زیر رادیکال به ازای تمام مقادیر $$x$$ یا مثبت است یا منفی. در اینجا عبارت زیر رادیکال همواره مثبت است، زیرا اگر به عنوان مثال $$x=0$$ را در $$ x ^ 2 - 4 x + 8 $$ جایگذاری کنیم، حاصل آن مقداری مثبت خواهد بود. بنابراین، دامنه این تابع، مجموعه‌ای از تمام اعداد حقیقی است.
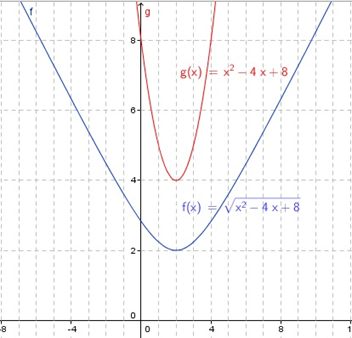
برای تعیین برد تابع، می‌توانیم $$ x ^ 2 - 4 x + 8 $$ را به صورت $$ ( x - 2 ) ^ 2 + 4 $$ بازنویسی کنیم. نمودار $$ ( x - 2 ) ^ 2 + 4 $$ یک سهمی با یک مینیمم در نقطه $$ ( 2 , 4 ) $$ است. از این رو، برد $$ x ^ 2 - 4 x + 8 $$ برابر با $$ [ 4, + ∞ ) $$ و برد تابع $$f(x)$$ برابر با $$[\sqrt 4,\sqrt {+∞})=[2,+∞) $$ خواهد بود.
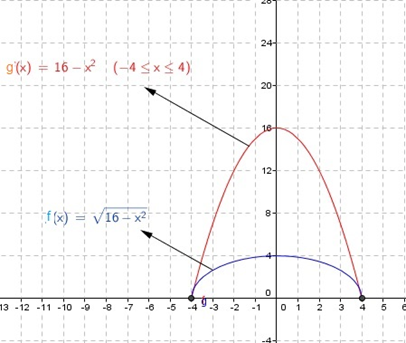
مثال نهم دامنه و برد توابع جبری و گویا
دامنه و برد تابع $$ f ( x ) = \sqrt { 1 6 - x ^ 2 } $$ را تعیین کنید.
حل: عبارت زیر یک رادیکال با فرجه زوج باید صفر یا مثبت باشد:
$$ \large 16-x^2≥0 $$
در نتیجه، داریم:
$$ \large x ^ 2 ≤ 1 6 , \\
\large x ≥ - 4, \; x ≤ 4 $$
بنابراین، دامنه تابع بازه بسته $$ [-4,4] $$ است. همانطور که در نمودار زیر مشاهده می‌کنید، تابع $$ 1 6 - x ^ 2 $$ یک سهمی با یک ماکزیمم در نقطه $$ (0,16) $$ است. بنابراین، برد آن $$ [0,16] $$ و در نتیجه برد تابع $$f(x)$$ بازه $$ [ \sqrt 0 , \sqrt { 1 6 } ] = [ 0 , 4 ] $$ خواهد بود.
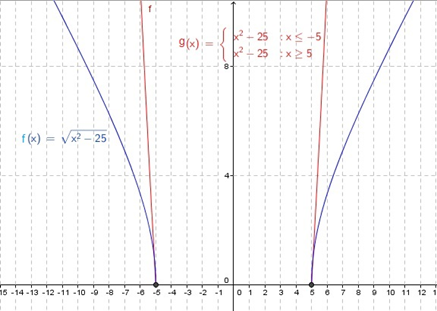
مثال دهم دامنه و برد توابع جبری و گویا
دامنه و برد تابع $$ f ( x ) = \sqrt { x ^ 2 - 2 5 } $$ را محاسبه کنید.
حل: از آنجا که تابع یک تابع رادیکالی با فرجه زوج است، داریم:
$$ \large x ^ 2- 2 5 ≥ 0 , \\
\large x ^ 2 ≥ 2 5 \\
\large x ≥ 5, \; x ≤ - 5 $$
به ازای مجموعه مقادیر $$x$$ در بازه $$ (-∞ , -5] \cup [5, +∞) $$، برد تابع $$ x^2-25 $$ و $$f(x)$$، بازه $$[0, +∞) $$ است.
معرفی فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس
برای آشنایی بیشتر با مباحث ریاضی دبیرستان، پیشنهاد می‌کنیم به مجموعه آموزش دروس دبیرستان و پیش دانشگاهی مراجعه کنید که توسط فرادرس تهیه شده است. این مجموعه، شامل دروس مقاطع مختلف تحصیلی متوسطه اول و دوم است که مطابق سرفصل‌های کتاب‌های درسی و با کیفیتی بالا توسط معلمان و دبیران کارآزموده تدوین شده‌اند.
- برای مشاهده فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه دانشگاهی
برای آشنایی بیشتر با مبحث دامنه و برد توابع، پیشنهاد می‌کنیم به فیلم آموزش ریاضی پایه دانشگاهی مراجعه کنید که توسط فرادرس و در ۱۲ ساعت و ۴۶ دقیقه تدوین شده است. در درس یکم این فیلم آموزشی که از ۱۰ درس تشکیل شده، مبحث مجموعه‌ها، مجموعه اعداد، توان، ب.م.م و ک.م.م بیان شده است. موضوع درس دوم چندجمله‌ای‌ها و اتحاد و تجزیه است. در درس سوم به موضوع نامساوی‌ها، نامعادلات، طول پاره‌خط، ضریب زاویه و معادله خط پرداخته شده است. درس چهارم درباره مثلثات است و در درس پنجم تصاعد حسابی و هندسی معرفی شده‌اند. موضوع مهم درس ششم تابع، دامنه و برد است. در ادامه، در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع بیان شده‌اند. توابع زوج و فرد، تابع یک به یک و تابع وارون موضوعات درس هشتم هستند. انواع تابع، شامل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح در درس نهم معرفی شده‌اند و در نهایت، در درس دهم به توابع نمایی و لگاریتمی پرداخته شده است.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد)
فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد) در ۵ ساعت و ۱۶ دقیقه و در قالب ۴ درس تهیه شده است. درس یکم این آموزش درباره مجموعه‌ها، چندجمله‌ای‌ها، اتحاد و تجزیه، نامساوی و نامعادلات است. در درس دوم، معادله درجه 2 مورد بررسی قرار گرفته است. موضوع درس سوم مثلثات است. در نهایت، در درس چهارم به تابع، دامنه و برد آن، تساوی دو تابع، اعمال جبری روی تابع، ترکیب توابع، توابع زوج و فرد، توابع یک به یک، وارون تابع، تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق، تابع جزء صحیح، تابع نمایی و تابع لگاریتمی پرداخته شده است.
- برای مشاهده فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد) + اینجا کلیک کنید.
سلام
ممنون از مطالب مفیدتون
در مثال اول دامنه و برد توابع چجوری دامنه تابع منفی بینهایت رو شامل میشه لطفا یه نگاه به مثال بکنید
سلام.
مثال بازنویسی شد.
سپاس از همراهی‌تان با مجله فرادرس.