حرکت غلتشی — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، درباره حرکت هماهنگ ساده بحث کردیم. در این آموزش، نوع دیگری از حرکت، یعنی حرکت غلتشی را معرفی خواهیم کرد.

اگر به چرخ‌‌های یک دوچرخه یا یک اتومبیل در حال حرکت نگاه کنید، می‌‌بینید که چرخ‌‌ها در عین حال که می‌‌چرخند جابه‌جا نیز می‌‌شوند. در واقع، چرخ‌‌ها علاوه بر حرکت دورانی، حرکت انتقالی نیز دارند. این نوع حرکت که ترکیبی از حرکت دورانی و حرکت انتقالی است را «حرکت غلتشی» (Rolling Motion) می‌‌نامند.

غلتش بدون لغزش

اتومبیلی را روی سطح یک جاده در نظر بگیرید. هنگامی که راننده گاز را تا انتها فشار می‌‌دهد، به گونه‌‌ای که چرخ‌‌ها بدون اینکه اتومبیل به جلو حرکت کند بچرخند، بین چرخ‌‌ها و سطح جاده اصطکاک جنبشی به وجود می‌‌آید. اگر راننده گاز را آهسته فشار دهد و موجب حرکت اتومبیل به سمت جلو شود، آن‌گاه چرخ‌‌ها بدون لغزش می‌‌غلتند.

فیلم آموزش فیزیک پایه 1 – جامع و کاربردی در فرادرس

کلیک کنید

در حقیقت، پایین چرخ نسبت به کف زمین ساکن است که نشان‌‌دهنده وجود اصطکاک ایستایی بین چرخ‌‌ها و سطح جاده خواهد بود. شکل زیر یک دوچرخه در حال حرکت را نشان می‌‌دهد که چرخ‌‌های آن با سطح جاده در تماس‌‌اند و با وجود اینکه در حال غلتیدن هستند، پایین چرخ‌‌ها اندکی تغییر شکل می‌‌دهند، اما نمی‌‌لغزند و نسبت به سطح جاده به ازای یک بازه زمانی ساکن هستند. بنابراین، باید بین چرخ و سطح جاده اصطکاک ایستایی وجود داشته باشد.

دوچرخه به سمت جلو حرکت می‌‌کند، در حالی که چرخ‌‌های آن هیچ لغزشی ندارند. پایینِ چرخی که اندکی تغییر شکل یافته به ازای یک بازه زمانی نسبت به سطح جاده ساکن است. تصویر فوق نشان می‌‌دهد که بالای چرخ غلتان به دلیل حرکتش تار به نظر می‌‌رسد، اما پایین چرخ فوراً ساکن می‌‌شود.

برای بررسی حرکت غلتشی بدون لغزش، ابتدا روابط بین متغیرهای خطی سرعت و شتاب مرکز جرم چرخ و متغیرهای زاویه‌‌ای را که حرکت چرخ را توصیف می‌‌کنند، به دست می‌‌آوریم. این حرکت در شکل زیر نشان داده شده است.

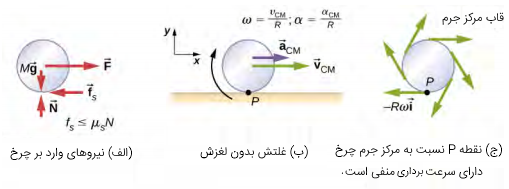
چرخ توسط نیروی $$\overrightarrow{F}$$ روی یک سطح افقی می‌‌غلتد. برای اینکه از لغزش چرخ جلوگیری شود، نیروی اصطکاک ایستایی $$\overrightarrow{f}_{S}$$ ($$|\overrightarrow{f}_{S}| \le \mu _S N$$) باید به اندازه کافی بزرگ باشد. بردارهای سرعت و شتاب خطی مرکز جرم هم‌‌جهت‌‌اند و نقطه P نسبت به سطح ساکن است. سرعت خطی در نقطه P نسبت به قاب مرکز جرم (CM) برابر است با $$-R\omega \hat{i}$$ که در آن، $$R$$ شعاع چرخ و $$\omega$$ سرعت زاویه‌‌ای چرخ حول محور آن است.

از آن‌جایی که چرخ در حال غلتش است، سرعت نقطه P نسبت به سطح برابر است با سرعت آن نسبت به مرکز جرم به علاوه سرعت مرکز جرم نسبت به سطح:

$$\large \overrightarrow { v } _ { P } = - R \omega \hat { i } + v _ { C M } \hat { i } \ldotp$$

سرعت نقطه P نسبت به سطح برابر با صفر است ($$v_p=0$$). از این رو، داریم:

$$\large v _ { C M } = R \omega \ldotp$$

رابطه (۱)

بنابراین، سرعت مرکز جرم چرخ برابر است با شعاع چرخ در سرعت زاویه‌‌ای حول محور آن. این رابطه ارتباط بین متغیر خطی (طرف چپ) و متغیر زاویه‌‌‌‌ای (طرف راست) را نشان می‌‌دهد.

اگر از رابطه (۱) نسبت به زمان مشتق بگیریم، شتاب خطی مرکز جرم به دست می‌‌آید. R یک ثابت است و از آن‌جایی که $$\alpha = \frac { d \omega } { d t }$$، داریم:

$$\large a _ { C M } = R \alpha \ldotp$$

رابطه (۲)

مسافت پیموده شده توسط چرخ را می‌‌توان با استفاده از شکل زیر برحسب متغیرهای زاویه‌‌ای به دست آورد. هنگامی که چرخ از نقطه A تا نقطه B می‌‌غلتد، سطح بیرونی آن دقیقاً همان مسافتی که پیموده شده است را روی زمین تصویر می‌‌کند که برابر است با $$d_{CM}$$. از طرف دیگر، طول سطح بیرونی (کمان AB) برابر با $$R\theta$$ است. بنابراین، خواهیم داشت:

$$\large d _ { C M } = R \theta \ldotp$$

رابطه (۳)

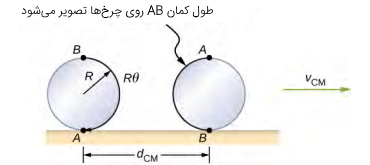
این رابطه نشان می‌‌دهد که طول کمان $$R\theta$$ متناظر با مسافت پیموده شده $$d_{CM}$$ مرکز جرم است.

مثال 1

یک استوانه توپر به جرم m و شعاع r، بدون اینکه بلغزد، از حالت سکون به سمت پایین یک سطح شیبدار شروع به غلتیدن می‌‌کند. (الف) شتاب این استوانه چقدر است؟ (ب) برای اینکه استوانه نلغزد، ضریب اصطکاک ایستایی باید در چه شرطی صدق کند؟

حل (الف): نمودار جسم آزاد برای این استوانه که شامل نیروی عمودی تکیه‌‌گاه، مؤلفه‌‌های نیروی وزن و نیروی اصطکاک ایستایی است، در شکل زیر نشان داده شده است.

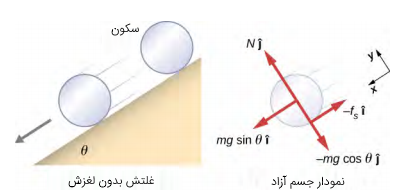
از آن‌جایی که هیچ لغزشی وجود ندارد، بزرگی نیروی اصطکاک باید کوچکتر یا مساوی با N باشد. مطابق با قانون دوم نیوتن داریم:

$$\large \sum F _ { x } = m a _ { x } ; \; \sum F _ { y } = m a _ { y } \ldotp$$

با جایگذاری نیروهای وارد شده به جسم، داریم:

$$\large \begin {split} m g \sin \theta - f _ { S } & = m ( a _ { C M } ) x , \\ N - m g \cos \theta & = 0 , \\ f _ { S } & \leq \mu _ { S } N , \end {split}$$

با استفاده از این روابط، می‌‌توان شتاب خطی مرکز جرم را به دست آورد:

$$\large ( a _ { C M } ) _ { x } = g ( \sin \theta - \mu _ { S } \cos \theta ) \ldotp$$

در این‌جا به دست آوردن شتاب خطی برحسب گشتاور لختی به حل مسئله کمک خواهد کرد. برای این کار از قانون دوم نیوتن برای دوران استفاده می‌‌کنیم:

$$\large \sum \tau _ { C M } = I _ { C M } \alpha \ldotp$$

گشتاورهای نیرو حول محور گذرنده از مرکز جرم استوانه محاسبه می‌‌شوند. در این مسئله، تنها گشتاور نیروی غیرصفر توسط نیروی اصطکاک ایجاد می‌‌شود. بنابراین، خواهیم داشت:

$$\large f _ { S } r = I _ { C M } \alpha \ldotp$$

از طرفی رابطه بین شتاب خطی و شتاب زاویه‌‌ای که قبلاً به دست آمد، به صورت زیر است:

$$\large ( a _ { C M } ) _ { x } = r \alpha \ldotp$$

این روابط را می‌‌توان برای محاسبه $$a_{CM}$$، $$\alpha$$ و $$f_S$$ برحسب گشتاور لختی به کار برد (در اینجا اندیس x را حذف کرده‌‌ایم). ابتدا $$a_{CM}$$ را برحسب مؤلفه عمودی نیروی وزن و نیروی اصطکاک می‌‌نویسیم:

$$\large a _ { C M } = g \sin \theta - \frac { f _ { S } } { m }$$

$$\large f _ { S } = \frac { I _ {C M } \alpha } { r } = \frac { I _ { C M } a _ { C M } } { r ^ { 2 } }$$

در نتیجه خواهیم داشت:

$$\large \begin {split} a _ { C M } & = g \sin \theta - \frac { I _ { CM } a _ {C M } } { m r ^ { 2 } } , \\ & = \frac { m g \sin \theta } { m + \left ( \dfrac { I _ { C M } } { r ^ { 2 } } \right ) } \ldotp \end {split}$$

همان‌طور که می‌‌بینیم، شتاب خطی به دست آمده مستقل از ضریب اصطکاک ایستایی $$\mu_{S}$$ است.

از آن‌جایی که یک استوانه توپر داریم، گشتاور لختی حول محور مرکزی برابر با $$I _ { C M } =\frac { m r ^ { 2 } } { 2 }$$ است. بنابراین، داریم:

$$\large a _ { C M } = \frac { m g \sin \theta } { m + \left ( \dfrac { m r ^ { 2 } } { 2 r ^ { 2 } } \right ) } = \frac { 2 } { 3 } g \sin \theta \ldotp$$

در نتیجه:

$$\large \alpha = \frac { a _ { C M } } { r } = \frac { 2 } { 3 r } g \sin \theta \ldotp$$

حل (ب): نیروی اصطکاک به صورت زیر به دست می‌‌آید:

$$\large \begin {align*} f _ { S } & = I _ { C M } \frac { \alpha } { r } = I _ { C M } \frac { ( a _ { C M } ) } { r ^ { 2 } } \\ &= \left ( \dfrac { I _ { C M } } { r ^ { 2 } } \right ) \left ( \dfrac { m g \sin \theta } { m + \left ( \dfrac { I _ { C M } } { r ^ { 2 } } \right ) } \right ) = \frac { m g I _ { C M } \sin \theta } { m r ^ { 2 } + I _ { C M } } \ldotp \end {align*}$$

چون این حرکت بدون لغزش اتفاق می‌‌افتد، $$f_S\le \mu _S N$$ است. بنابراین، با جایگذاری جواب به دست آمده در این شرط و با توجه به اینکه $$N=mg \cos \theta$$ است، داریم:

$$\large \frac { m g I _ { C M } \sin \theta } { m r ^ { 2 } + I _ { C M } } \leq \mu _ { S } mg \cos \theta$$

یا

$$\large \mu _ { S } \geq \frac { \tan \theta } { 1 + \left ( \dfrac { m r ^ { 2 } } { I _ { C M } } \right ) } \ldotp$$

برای استوانه توپر این شرط به صورت زیر خواهد بود:

$$\large \mu _ { S } \geq \frac { \tan \theta } { 1 + \left ( \dfrac { 2 m r ^ { 2 } } { m r ^ { 2 } } \right ) } = \frac { 1 } { 3 } \tan \theta \ldotp$$

نتایج این مثال را می‌توان به صورت زیر نوشت:

• شتاب خطی به طور خطی با $$\sin \theta$$ متناسب است. بنابراین، اگر زاویه شیب بزرگتر باشد، شتاب خطی بزرگتر است. شتاب زاویه‌‌ای نیز به طور خطی با $$\sin \theta$$ و به طور معکوس با شعاع استوانه متناسب است. در صورتی که شعاع بزرگتر باشد، شتاب زاویه‌‌ای کوچکتر است.
• برای اینکه غلتش بدون لغزش رخ دهد، باید ضریب اصطکاک ایستایی بزرگتر یا مساوی با $$\frac{1}{3} \tan \theta$$ باشد. بنابراین، اگر زاویه شیب بزرگتر باشد، ضریب اصطکاک ایستایی نیز باید بزرگتر شود تا مانع لغزش استوانه گردد.

در مثال قبل نشان دادیم شتاب جسمی که از بالای یک سطح شیبدار با اصطکاک بدون لغزش می‌‌غلتد، برابر است با:

$$\large a _ { C M } = \frac { m g \sin \theta } { m + \left ( \dfrac { I _ { C M } } { r ^ { 2 } } \right ) } \ldotp$$

این رابطه برای حل مسائل مربوط به حرکت غلتشی بدون لغزش بسیار کاربرد دارد. توجه داشته باشید که این شتاب نسبت به شتاب جسمی که روی یک سطح بدون اصطکاک، بدون چرخش به سمت پایین غلت می‌‌خورد، کمتر است. همچنین، برای دو استوانه چرخان با لختی‌‌های دورانی متفاوت، این شتاب متفاوت خواهد بود.

حرکت غلتشی همراه با لغزش

در حرکت غلتشی همراه با لغزش باید از ضریب اصطکاک جنبشی که منجر به نیروی اصطکاک جنبشی می‌‌شود، استفاده کنیم.

فیلم آموزش فیزیک پایه 1 – مرور و حل تست در فرادرس

کلیک کنید

این حرکت در شکل زیر نشان داده شده است. در حالتی که لغزش وجود دارد، $$v_{CM}-R\omega \neq 0$$ است، زیرا نقطه P روی چرخ نسبت به سطح ساکن نیست و $$v_p \neq 0$$ است. بنابراین، $$\omega \neq \frac{v_{CM}}{R}$$ و $$\alpha \neq \frac{a_{CM}}{R}$$ است.

مثال 2

یک استوانه توپر به جرم m و شعاع r روی یک سطح شیبدار از حالت سکون به سمت پایین می‌‌غلتد و دچار لغزش می‌‌شود. (الف) شتاب خطی استوانه را به دست آورید. (ب) شتاب زاویه‌‌ای حول محور گذرنده از مرکز جرم چقدر است؟

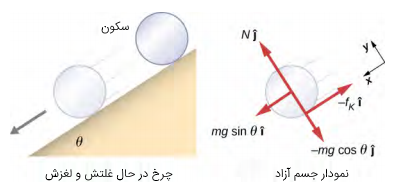
حل: مشابه مثال قبل، برای به دست آوردن شتاب از قانون دوم نیوتن استفاده می‌‌کنیم.

جمع نیروها در راستای محور y مساوی با صفر است؛ بنابراین، نیروی اصطکاک برابر با $$f_k=\mu _k N = \mu _k m g \cos \theta$$ خواهد بود. قانون دوم نیوتن در راستای x به صورت زیر است:

$$\large \sum F _ { x } = m a _ { x }$$

$$\large mg \sin \theta - \mu _ { k } m g \cos \theta = m ( a _ { C M } ) _ { x }$$

یا

$$\large ( a _ { C M } ) _ { x } = g ( \sin \theta - \mu _ { k } \cos \theta ) \ldotp$$

تنها گشتاور نیرو حول محور گذرنده از مرکز جرم توسط نیروی اصطکاک حاصل می‌‌شود. بنابراین، قانون دوم نیوتن برای دوران به صورت زیر است:

$$\large \sum \tau _ { C M } = I _ { C M } \alpha ,$$

$$\large f _ { k } r = I _ { C M } \alpha = \frac { 1 } { 2 } m r ^ { 2 } \alpha \ldotp$$

در نتیجه، خواهیم داشت:

$$\large \alpha = \frac { 2 f _ { k } } { m r } = \frac { 2 \mu _ { k } g \cos \theta } { r } \ldotp$$

شتاب زاویه‌‌ای حول محور دوران به طور خطی با نیروی عمودی تکیه‌‌گاه متناسب است که به کسینوس زاویه شیب بستگی دارد. در صورتی که $$\theta$$ به ۹۰ درجه میل کند، این نیرو و در نتیجه شتاب زاویه‌‌ای به سمت صفر میل خواهند کرد.

پایستگی انرژی مکانیکی در حرکت غلتشی

یک جسم غلتان، بسته به سیستم مورد نظر، می‌‌تواند انرژی جنبشی دورانی، انرژی جنبشی انتقالی و انرژی پتانسیل داشته باشد. بنابراین، انرژی مکانیکی کل یک جسم غلتان برابر است با:

$$\large E _ { T } = \frac { 1 } { 2 } m v ^ { 2 } _ { C M } + \frac { 1 } { 2 } I _ { C M } \omega ^ { 2 } + m g h \ldotp$$

در غیاب نیروهای ناپایستار که انرژی را خارج از سیستم در قالب گرما می‌‌گیرند، انرژی کل جسم غلتان بدون لغزش پایسته است و در طول حرکت ثابت می‌‌ماند، اما برای جسم غلتانی که می‌‌لغزد، انرژی پایسته نیست.

شاید این پرسش برایتان پیش آید که چرا برای حالتی که جسم بدون لغزش می‌‌غلتد انرژی پایسته می‌‌ماند، در حالی که نیروی اصطکاک ایستایی یک نیروی ناپایستار است. پاسخ این پرسش به شکل مربوط به حرکت غلتشی بدون لغزش بر می‌‌گردد. نقطه P که با سطح در تماس است، نسبت به سطح ساکن است؛ بنابراین، جابه‌جایی بسیار کوچک این نقطه نسبت به سطح و در نتیجه کار انجام شده توسط نیروی اصطکاک ایستایی صفر خواهد بود.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آموزش مکانیک تحلیلی 1
• قانون جهانی گرانش نیوتن — به زبان ساده
• تانسور چیست؟ — مفاهیم اصلی

^^