تقویت کننده انتگرال گیر — به زبان ساده (+ دانلود فیلم آموزش رایگان)

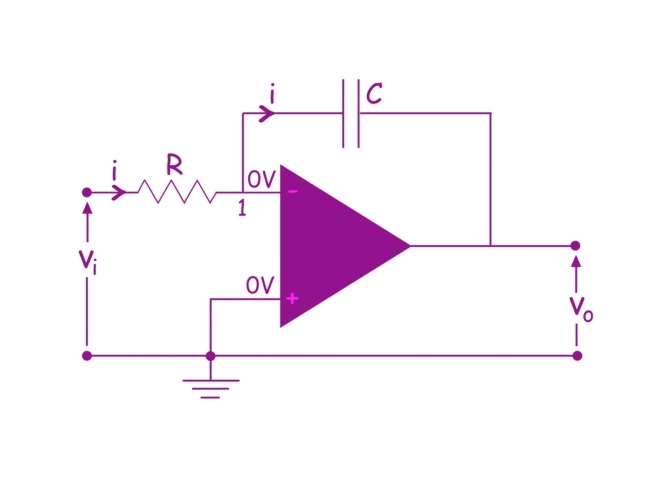
در آموزش‌های پیشین مجله فرادرس، با تقویت‌کننده‌های عملیاتی یا آپ‌امپ‌ها آشنا شدیم. همچنین یکی از انواع این تقویت‌کننده‌ها به نام تقویت‌کننده معکوس‌کننده را بررسی کردیم. در این آموزش، تقویت کننده انتگرال گیر را معرفی خواهیم کرد.

همان‌طور که می‌دانیم، تقویت‌کننده‌‌های عملیاتی، به عنوان قسمتی از تقویت‌کننده‌های فیدبک مثبت یا منفی به کار می‌روند. از آپ‌امپ‌ها می‌توان مشابه یک مدار جمع‌کننده یا مدار تفریق‌کننده نیز استفاده کرد که در آن‌ها یک مقاومت خالص برای هر دو حلقه ورودی و فیدبک به کار رفته است.

فیلم آموزش الکترونیک 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

اگر در یک تقویت‌کننده معکوس، المان فیدبک مقاومتی خالص $$R_f$$ را با یک المان راکتانسی وابسته به فرکانس $$X$$ مانند خازن $$C$$ جایگزین کنیم، چه اتفاقی خواهد افتاد؟ این تغییر چه تأثیری بر ولتاژ خروجی آپ‌امپ دارد؟

با تعویض مقاومت فیدبک با یک خازن، یک مدار $$RC$$ به دست می‌آید که در مسیر فیدبک تقویت‌کننده عملیاتی قرار دارد. در این حالت، یک نوع دیگر از مدارهای تقویت‌کننده عملیاتی به‌ دست می‌آید که به مدار «تقویت‌کننده انتگرال‌گیر» (Integrator Amplifier) معروف است. مدار این تقویت‌کننده در شکل زیر نشان داده شده است.

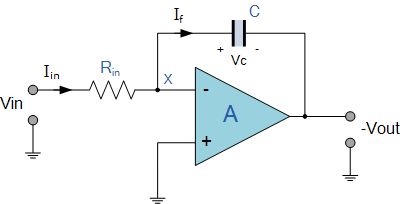
همان‌طور که از نام آن پیداست، یک مدار تقویت‌کننده انتگرال‌گیر عملکردی مشابه انتگرال در ریاضیات دارد. بنابراین، می‌توان خروجی آن را بر اساس تغییرات ولتاژ ورودی در طول زمان به دست آورد. به عبارت دیگر، ولتاژ خروجی آپ‌امپ انتگرال‌گیر، متناسب با انتگرال ولتاژ ورودی است.

می‌توان گفت که دامنه سیگنال خروجی این آپ‌امپ به مدت زمان حضور ولتاژ ورودی وابسته است. در طول این مدت، جریان با عبور از حلقه فیدبک، خازن را شارژ یا دشارژ می‌کند. این عمل تا جایی ادامه دارد که فیدبک منفی مورد نیاز از طریق خازن تأمین شود.

زمانی که ولتاژ پله $$V_{in}$$ برای اولین بار به ورودی تقویت‌کننده انتگرال‌گیر اعمال شود، خازنِ بدون شارژ $$C$$، مانند یک مقاومت بسیار کوچک عمل می‌کند. در این حالت، خازن اتصال کوتاه است و تا وقتی که بین دو صفحه آن اختلاف پتانسیل وجود دارد، همه جریان از مقاومت ورودی $$R_{in}$$ عبور می‌کند. بنابراین، هیچ جریانی از ورودی تقویت‌کننده (نقطه X) نمی‌گذرد. پس این نقطه به عنوان زمین مجازی در نظر گرفته می‌شود و تقویت‌کننده هیچ‌گونه خروجی نخواهد داشت. از آن‌جایی که امپدانس خازن در این حالت بسیار کم است، نسبت $$X_C/R_{in}$$ نیز بسیار کوچک خواهد بود. این نسبت پایین باعث می‌شود بهره ولتاژ تقویت‌کننده کمتر از یک باشد (مدار دنبال‌‌کننده ولتاژ).

با گذشت زمان و به دلیل حضور ولتاژ ورودی، خازن فیدبک $$C$$‌ شارژ می‌شود و امپدانس $$X_C$$ آن شروع به افزایش می‌کند. افزایش امپدانس، متناسب با نرخ شارژ خازن است و سرعت شارژ خازن توسط ثابت زمانی $$T$$ مدار RC تعیین می‌شود. وجود فیدبک منفی منجر به تولید ولتاژ خروجی در آپ‌امپ و در نتیجه حفظ زمین مجازی در ورودی آن خواهد شد.

در شکل بالا مشاهده می‌کنیم که خازن بین ورودی منفی آپ‌امپ (که هم‌پتانسیل با زمین است) و خروجی آن (که منفی است) قرار دارد. با افزایش تدریجی ولتاژ خازن $$V_C$$، جریان عبوری $$I_f$$ از آن کاهش یافته و امپدانس آن زیاد می‌شود. بنابراین، با افزایش تدریجی $$X_C$$، نسبت $$X_C/R_{in}$$ نیز زیاد می‌شود و در نتیجه، ولتاژ خروجی به صورت خطی افزایش می‌یابد. افزایش ولتاژ خروجی تا جایی ادامه دارد که خازن به طور کامل شارژ شود.

در نقطه شارژ کامل، خازن عملکردی مشابه مدار باز دارد و هیچ‌گونه جریان DC را از خود عبور نمی‌دهد. بنابراین، نسبت خازن فیدبک به مقاومت ورودی $$X_C/R_{in}$$ بسیار زیاد است و بهره بی‌نهایت می‌شود. بی‌نهایت شدن بهره (مشابه بهره آپ‌امپ‌های مدار باز) سبب اشباع شدن تقویت‌کننده خواهد شد. این موضوع در شکل زیر نشان داده شده است. اشباع، زمانی رخ می‌دهد که ولتاژ خروجی تقویت‌کننده نسبت به ولتاژ تغذیه یا دیگر ولتاژها به شدت و به طور غیر قابل کنترل نوسان کند.

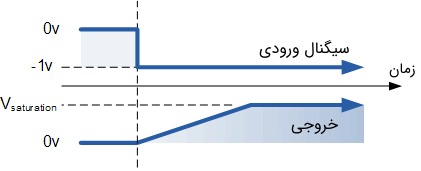
نرخ افزایش (سرعت) ولتاژ خروجی، توسط مقدار خازن و مقاومت تعیین می‌شود. به عبارت دقیق‌تر، ثابت زمانی مدار RC سرعت افزایش را مشخص می‌کند. با تغییر مقدار خازن $$C$$ و مقدار مقاومت $$R$$، می‌توان ثابت زمانی RC را تغییر داد. بنابراین، با تغییر ثابت زمانی RC، زمان به اشباع رسیدن ولتاژ خروجی نیز تغییر می‌کند.
اگر یک سیگنال با تغییرات ثابت مانند سیگنال موج مربعی به ورودی تقویت‌کننده انتگرال‌گیر اعمال کنیم، خازن شارژ و دشارژ می‌شود. این کار باعث به وجود آمدن سیگنال دندان‌اره‌ای در خروجی خواهد شد. از آن‌جایی که در فرکانس‌های بالاتر، خازن زمان کمتری برای شارژ کامل دارد، این خروجی با تغییر ثابت زمانی مدار RC تغییر خواهد کرد. این نوع مدار با نام مدار تولیدکننده شیب (Ramp) شناخته می‌شود. تابع انتقال این مدار در ادامه ارائه شده است.

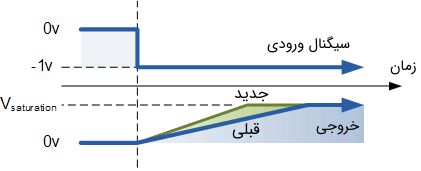
با توجه به اصول پایه فیزیک می‌دانیم که ولتاژ روی صفحه‌های خازن، برابر با بار روی خازن تقسیم بر ظرفیت آن ($$Q/C$$) است. بنابراین، ولتاژ در خروجی $$V_{out}$$ خازن، برابر با $$Q/C$$ است. اگر خازن شارژ و دشارژ شود، میزان تغییر بار در خازن به صورت زیر محاسبه می‌شود:

$$\large V_C = \frac {Q} {C}, \,\,\,\;\; V_C = V_X - V_{out} = 0-V_{out} \\ \large \Rightarrow - \frac {dV _{out}} {dt} =\frac {dQ} {C dt } = \frac { 1 } { C } \frac { dQ } { C dt }$$

که در آن، $$d Q / dt$$ همان تعریف جریان الکتریکی است و از آن‌جایی که ولتاژ گره آپ‌امپ انتگرال‌گیر در ترمینال ورودی منفی صفر است ($$V_X = 0$$)، جریان ورودی $$I_{in}$$ از مقاومت عبوری $$R_{in}$$ می‌گذرد. این جریان، برابر است با:‌

$$\large I _ {in} = \frac { V _ {in} - 0 } { R _ { in} } = \frac { V _ {in} } {I _ {in }}$$

جریان عبوری از خازن فیدبک $$C$$ نیز به صورت زیر است:

$$\large I _ f = C \frac {d V _ {out} } {d t } = C \frac {d Q } { C dt } = \frac { d Q } { d t } = \frac { dV _ {out} \cdot C } { d t }$$

اگر فرض کنیم امپدانس ورودی آپ‌امپ بی‌نهایت است (آپ‌امپ ایده‌آل باشد)، در این صورت هیچ جریانی از ترمینال‌های آن عبور نمی‌کند. بنابراین، معادله گره در ترمینال ورودی منفی به صورت زیر است:

$$\large I _ { in } = I _ f = \frac { V _ {in}} { R _ {in} } = \frac { d V _ {out} \cdot C } {d t } \\ \large \frac { V _ {in}} {V _ { out}} \times \frac {dt } { R _ {in} \cdot C } = 1$$

در نتیجه، ولتاژ خروجی آپ‌امپ انتگرال‌گیر ایده‌آل به صورت زیر بیان می‌شود:

$$\large V {out} = - \frac {1 } {R_{in} C }\int _ 0 ^ t { V_{in} dt} = - \int _ 0 ^ t { V_{in} \frac { dt} { R_{in} \cdot C}}$$

معادله بالا را می‌توان به شکل زیر نوشت:

$$\large V _ {out} = - \frac {1 } { j \omega RC} V _ {in}$$

که درآن، $$\omega = 2 \pi f$$، و ولتاژ خروجی $$V _ {out}$$ برابر با $$1/RC$$ انتگرال ولتاژ‌ ورودی $$V_ {in}$$ است. علامت منفی در فرمول ولتاژ خروجی، نشان دهنده اختلاف فاز $$180$$ درجه‌ای آن نسبت به ولتاژ ورودی است. دلیل این امر، آن است که سیگنال ورودی مستقیماً به ترمینال منفی آپ‌امپ متصل می‌شود.

تقویت کننده انتگرال گیر AC

اگر سیگنال ورودی موج مربعی بالا را با یک سیگنال سینوسی با فرکانس متغیر جایگزین کنیم، آپ‌امپ، دیگر مشابه یک انتگرال‌گیر رفتار نمی‌کند. در این حالت، عملکرد تقویت‌کننده مانند یک فیلتر پایین‌گذر است. همان‌طور که از نام آن پیداست، فیلتر پایین‌گذر سیگنال‌های با فرکانس پایین را عبور می‌دهد و سیگنال‌های با فرکانس بالا را حذف می‌کند.

فیلم آموزش حل تمرین الکترونیک ۱ در فرادرس

کلیک کنید

در سیگنال‌هایی با فرکانس صفر یا همان DC، خازن مانند یک مدار باز عمل می‌کند. در این حالت، خازن تمام ولتاژ فیدبک را مسدود می‌کند و فیدبک منفی بسیار ناچیزی از خروجی به ورودی تقویت‌کننده می‌رسد. بنابراین، تنها به دلیل وجود خازن فیدبک $$C$$، تقویت‌کننده در سیگنال‌های DC رفتاری مشابه یک تقویت‌کننده مدار باز معمولی دارد. در این حالت، بهره تقویت‌کننده مدار باز، به اندازه‌ای زیاد است که منجر به اشباع ولتاژ خروجی می‌شود.

در این مدار، یک مقاومت بزرگ با یک خازن به صورت موازی متصل شده است. این خازن همواره شارژ و دشارژ می‌شود. موازی بودن مقاومت فیدبک $$R_2$$ با خازن $$C$$ باعث به وجود آمدن یک تقویت‌کننده معکوس با بهره حلقه بسته بی‌نهایت $$R_2 / R_1$$ می‌شود. این ویژگی سبب خواهد شد تقویت‌کننده در فرکانس‌های مختلف، رفتار یکسانی نشان ندهد. به این صورت که در فرکانس‌های پایین، مانند یک انتگرال‌گیر استاندارد عمل کرده و در فرکانس‌های بالا به دلیل کاهش بهره در اثر راکتانس خازنی، مقاومت فیدبک $$R_2$$ را از مدار خارج می‌کند.

شکل زیر، آپ‌امپ انتگرال‌گیر AC با کنترل بهره DC را نشان می‌دهد.

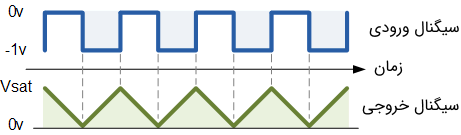
تقویت‌کننده AC، با تقویت‌کننده انتگرال‌گیر DC تفاوت‌هایی دارد. در تقویت‌کننده انتگرال‌گیر DC، ولتاژ خروجی در هر لحظه برابر با انتگرال شکل موج ورودی است. به عنوان مثال، زمانی که ورودی یک شکل موج مربعی باشد، شکل موج خروجی مثلثی خواهد بود. در حالی که اگر یک شکل موج سینوسی را به انتگرال‌گیر AC اعمال کنیم، خروجی یک شکل موج سینوسی دیگر خواهد بود. با این تفاوت که شکل موج خروجی، $$90$$ درجه با شکل موج ورودی اختلاف فاز دارد.

علاوه بر این، زمانی که ورودی مثلثی باشد، شکل موج خروجی هم‌چنان سینوسی است. این رفتار، اساس یک فیلتر اکتیو پایین‌گذر را نشان می‌دهد. فرکانس گوشه این فیلتر به صورت زیر محاسبه می‌شود:

$$\large f _ 0 = \frac {1 } { 2 \pi C R _ 2 }$$

بهره ولتاژ DC و بهره ولتاژ AC نیز به ترتیب برابرند با:

$$\large A _ {v0} = - \frac {R_2} {R _ 1}$$

$$\large A _ v = - \frac {R _ 2} {R _ 1} \times \frac {1 } { (1+ 2 \pi f C R _ 2 )}$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تقویت کننده های الکترونیکی – مجموعه مقالات جامع وبلاگ فرادرس
• انواع تقویت‌ کننده‌ ها از نظر نوع عملکرد تقویتی — به زبان ساده
• بایاس ترانزیستور (Transistor Biasing) — از صفر تا صد

^^