مساله تقسیم بندی در بهینه سازی — به زبان ساده

در این مطلب، روش حل مساله تقسیم بندی در بهینه سازی بیان شده است. همچنین، پیاده‌سازی روش آموزش داده شده در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «سی» (C)، «جاوا» (Java)، «پایتون ۳» (Python 3) و «پی‌اچ‌پی» (PHP) انجام شده است. «مساله تقسیم بندی» (Partition Problem) یکی از انواع مسائل بهینه‌سازی است. در مساله تقسیم بندی، هدف تقسیم کردن مساله به دو زیر مجموعه به گونه‌ای است که مجموع مقادیر موجود در هر دو زیر مجموعه، با هم برابر باشد. مثال زیر در این راستا قابل توجه است:

arr[] = {1, 5, 11, 5}
Output: true 
The array can be partitioned as {1, 5, 5} and {11}

arr[] = {1, 5, 3}
Output: false 
The array cannot be partitioned into equal sum sets.

در ادامه، دو گام اساسی برای حل این مساله بیان شده‌اند.

1. مجموع آرایه را محاسبه کن. اگر مجموع عددی فرد باشد، دو زیر مجموعه با مجموع برابر وجود نخواهد داشت. بنابراین، مقدار False را بازگردان.
2. اگر مجموع عناصر آرایه زوج است، مجموع تقسیم بر ۲ را محاسبه و سپس، زیرمجموعه‌ای از آرایه با مجموع برابر با $$\frac{sum}{2}$$ را پیدا کن.

گام اول ساده و گام دوم مهم و حیاتی است. برای پیاده‌سازی گام دوم می‌توان از راهکار بازگشتی یا برنامه‌نویسی پویا استفاده کرد.

راهکار بازگشتی برای حل مساله تقسیم بندی

در ادامه، راهکار بازگشتی برای پیاده‌سازی گام دوم بیان شده در بالا، ارائه شده است.

(isSubsetSum(arr, n, sum/2 تابعی است که اگر زیرمجموعه‌ای از آرایه [arr[0..n-1 با مجموع برابر با $$\frac{Sum}{2}$$ وجود داشت، مقدار True را باز می‌گرداند.

مساله isSubsetSum را می‌توان به دو زیر مسأله تقسیم کرد.

1. ()isSubsetSum بدون در نظر گرفتن آخرین عنصر (کاهش n به n-1)
2. isSubsetSum با در نظر گرفتن آخرین عنصر (کاهش $$\frac{Sum}{2}$$ با [arr[n-1 و n تا n-1)

اگر هر یک از دو زیرمسأله بالا مقدار true را بازگرداند، مقدار true را بازگردان.

isSubsetSum (arr, n, sum/2) = isSubsetSum (arr, n-1, sum/2) || isSubsetSum (arr, n-1, sum/2 – arr[n-1])

حل مساله تقسیم بندی به روش بازگشتی در ++C

// A recursive C++ program for partition problem  
#include <bits/stdc++.h> 
using namespace std; 
  
// A utility function that returns true if there is  
// a subset of arr[] with sun equal to given sum  
bool isSubsetSum (int arr[], int n, int sum)  
{  
    // Base Cases  
    if (sum == 0)  
        return true;  
    if (n == 0 && sum != 0)  
        return false;  
  
    // If last element is greater than sum, then  
    // ignore it  
    if (arr[n-1] > sum)  
       return isSubsetSum (arr, n-1, sum);  
  
    /* else, check if sum can be obtained by any of  
        the following  
        (a) including the last element  
        (b) excluding the last element  
    */
    return isSubsetSum (arr, n-1, sum) ||  
        isSubsetSum (arr, n-1, sum-arr[n-1]);  
}  
  
// Returns true if arr[] can be partitioned in two  
// subsets of equal sum, otherwise false  
bool findPartiion (int arr[], int n)  
{  
    // Calculate sum of the elements in array  
    int sum = 0;  
    for (int i = 0; i < n; i++)  
    sum += arr[i];  
  
    // If sum is odd, there cannot be two subsets  
    // with equal sum  
    if (sum%2 != 0)  
    return false;  
  
    // Find if there is subset with sum equal to  
    // half of total sum  
    return isSubsetSum (arr, n, sum/2);  
}  
  
// Driver program to test above function  
int main()  
{  
    int arr[] = {3, 1, 5, 9, 12};  
    int n = sizeof(arr)/sizeof(arr[0]);  
    if (findPartiion(arr, n) == true)  
        cout << "Can be divided into two subsets "
                "of equal sum";  
    else
        cout << "Can not be divided into two subsets"
                " of equal sum";  
    return 0;  
}  
  
// This code is contributed by rathbhupendra

حل مساله تقسیم بندی به روش بازگشتی در C

// A  recursive C program for partition problem 
#include <stdio.h> 
#include <stdbool.h> 
  
// A utility function that returns true if there is  
// a subset of arr[] with sun equal to given sum 
bool isSubsetSum (int arr[], int n, int sum) 
{ 
   // Base Cases 
   if (sum == 0) 
     return true; 
   if (n == 0 && sum != 0) 
     return false; 
  
   // If last element is greater than sum, then  
   // ignore it 
   if (arr[n-1] > sum) 
     return isSubsetSum (arr, n-1, sum); 
  
   /* else, check if sum can be obtained by any of  
      the following 
      (a) including the last element 
      (b) excluding the last element 
   */
   return isSubsetSum (arr, n-1, sum) ||  
          isSubsetSum (arr, n-1, sum-arr[n-1]); 
} 
  
// Returns true if arr[] can be partitioned in two 
//  subsets of equal sum, otherwise false 
bool findPartiion (int arr[], int n) 
{ 
    // Calculate sum of the elements in array 
    int sum = 0; 
    for (int i = 0; i < n; i++) 
       sum += arr[i]; 
  
    // If sum is odd, there cannot be two subsets  
    // with equal sum 
    if (sum%2 != 0) 
       return false; 
  
    // Find if there is subset with sum equal to 
    // half of total sum 
    return isSubsetSum (arr, n, sum/2); 
} 
  
// Driver program to test above function 
int main() 
{ 
  int arr[] = {3, 1, 5, 9, 12}; 
  int n = sizeof(arr)/sizeof(arr[0]); 
  if (findPartiion(arr, n) == true) 
     printf("Can be divided into two subsets "
            "of equal sum"); 
  else
     printf("Can not be divided into two subsets"
            " of equal sum"); 
  return 0; 
}

حل مساله تقسیم بندی به روش بازگشتی در جاوا

// A recursive Java solution for partition problem 
import java.io.*; 
  
class Partition 
{ 
    // A utility function that returns true if there is a 
    // subset of arr[] with sun equal to given sum 
    static boolean isSubsetSum (int arr[], int n, int sum) 
    { 
        // Base Cases 
        if (sum == 0) 
            return true; 
        if (n == 0 && sum != 0) 
            return false; 
  
        // If last element is greater than sum, then ignore it 
        if (arr[n-1] > sum) 
            return isSubsetSum (arr, n-1, sum); 
  
        /* else, check if sum can be obtained by any of 
           the following 
        (a) including the last element 
        (b) excluding the last element 
        */
        return isSubsetSum (arr, n-1, sum) || 
               isSubsetSum (arr, n-1, sum-arr[n-1]); 
    } 
  
    // Returns true if arr[] can be partitioned in two 
    // subsets of equal sum, otherwise false 
    static boolean findPartition (int arr[], int n) 
    { 
        // Calculate sum of the elements in array 
        int sum = 0; 
        for (int i = 0; i < n; i++) 
            sum += arr[i]; 
  
        // If sum is odd, there cannot be two subsets 
        // with equal sum 
        if (sum%2 != 0) 
            return false; 
  
        // Find if there is subset with sum equal to half 
        // of total sum 
        return isSubsetSum (arr, n, sum/2); 
    } 
  
    /*Driver function to check for above function*/
    public static void main (String[] args) 
    { 
  
        int arr[] = {3, 1, 5, 9, 12}; 
        int n = arr.length; 
        if (findPartition(arr, n) == true) 
            System.out.println("Can be divided into two "+ 
                                "subsets of equal sum"); 
        else
            System.out.println("Can not be divided into " + 
                                "two subsets of equal sum"); 
    } 
} 
/* This code is contributed by Devesh Agrawal */

حل مساله تقسیم بندی به روش بازگشتی در پایتون ۳

# A recursive Python3 program for  
# partition problem 
  
# A utility function that returns  
# true if there is a subset of 
# arr[] with sun equal to given sum 
def isSubsetSum (arr, n, sum): 
    # Base Cases 
    if sum == 0: 
        return True
    if n == 0 and sum != 0: 
        return False
  
    # If last element is greater than sum, then  
    # ignore it 
    if arr[n-1] > sum: 
        return isSubsetSum (arr, n-1, sum) 
  
    ''' else, check if sum can be obtained by any of  
    the following 
    (a) including the last element 
    (b) excluding the last element'''
      
    return isSubsetSum (arr, n-1, sum) or isSubsetSum (arr, n-1, sum-arr[n-1]) 
  
# Returns true if arr[] can be partitioned in two 
# subsets of equal sum, otherwise false 
def findPartion (arr, n): 
    # Calculate sum of the elements in array 
    sum = 0
    for i in range(0, n): 
        sum += arr[i] 
    # If sum is odd, there cannot be two subsets  
    # with equal sum 
    if sum % 2 != 0: 
        return false 
  
    # Find if there is subset with sum equal to 
    # half of total sum 
    return isSubsetSum (arr, n, sum // 2) 
  
# Driver program to test above function 
arr = [3, 1, 5, 9, 12] 
n = len(arr) 
if findPartion(arr, n) == True: 
    print ("Can be divided into two subsets of equal sum") 
else: 
    print ("Can not be divided into two subsets of equal sum") 
      
# This code is contributed by shreyanshi_arun.

حل مساله تقسیم بندی به روش بازگشتی در #C

// A recursive C# solution for partition problem 
using System; 
  
class GFG 
{ 
    // A utility function that returns true if there is a 
    // subset of arr[] with sun equal to given sum 
    static bool isSubsetSum (int []arr, int n, int sum) 
    { 
        // Base Cases 
        if (sum == 0) 
            return true; 
        if (n == 0 && sum != 0) 
            return false; 
  
        // If last element is greater than sum, then ignore it 
        if (arr[n-1] > sum) 
            return isSubsetSum (arr, n-1, sum); 
  
        /* else, check if sum can be obtained by any of 
        the following 
        (a) including the last element 
        (b) excluding the last element 
        */
        return isSubsetSum (arr, n-1, sum) || 
               isSubsetSum (arr, n-1, sum-arr[n-1]); 
    } 
  
    // Returns true if arr[] can be partitioned in two 
    // subsets of equal sum, otherwise false 
    static bool findPartition (int []arr, int n) 
    { 
        // Calculate sum of the elements in array 
        int sum = 0; 
        for (int i = 0; i < n; i++) 
            sum += arr[i]; 
  
        // If sum is odd, there cannot be two subsets 
        // with equal sum 
        if (sum%2 != 0) 
            return false; 
  
        // Find if there is subset with sum equal to half 
        // of total sum 
        return isSubsetSum (arr, n, sum/2); 
    } 
  
    // Driver function  
    public static void Main () 
    { 
  
        int []arr = {3, 1, 5, 9, 12}; 
        int n = arr.Length; 
        if (findPartition(arr, n) == true) 
            Console.Write("Can be divided into two "+ 
                          "subsets of equal sum"); 
        else
            Console.Write("Can not be divided into " + 
                          "two subsets of equal sum"); 
    } 
} 
  
// This code is contributed by Sam007

حل مساله تقسیم بندی به روش بازگشتی در PHP

<?php 
// A recursive PHP solution for partition problem 
  
// A utility function that returns true if there is  
// a subset of arr[] with sun equal to given sum  
function isSubsetSum ($arr, $n, $sum)  
{  
    // Base Cases  
    if ($sum == 0)  
        return true;  
    if ($n == 0 && $sum != 0)  
        return false;  
      
    // If last element is greater than  
    // sum, then ignore it  
    if ($arr[$n - 1] > $sum)  
        return isSubsetSum ($arr, $n - 1, $sum);  
      
    /* else, check if sum can be obtained  
       by any of the following  
        (a) including the last element  
        (b) excluding the last element  
    */
    return isSubsetSum ($arr, $n - 1, $sum) ||  
           isSubsetSum ($arr, $n - 1,  
                        $sum - $arr[$n - 1]);  
}   
  
// Returns true if arr[] can be partitioned  
// in two subsets of equal sum, otherwise false  
function findPartiion ($arr, $n)  
{  
    // Calculate sum of the elements 
    // in array  
    $sum = 0;  
    for ($i = 0; $i < $n; $i++)  
    $sum += $arr[$i];  
  
    // If sum is odd, there cannot be  
    // two subsets with equal sum  
    if ($sum % 2 != 0)  
    return false;  
  
    // Find if there is subset with sum 
    // equal to half of total sum  
    return isSubsetSum ($arr, $n, $sum / 2);  
}  
  
// Driver Code 
$arr = array(3, 1, 5, 9, 12);  
$n = count($arr);  
if (findPartiion($arr, $n) == true)  
    echo "Can be divided into two subsets of equal sum";  
else
    echo "Can not be divided into two subsets of equal sum";  
  
// This code is contributed by rathbhupendra 
?>

خروجی قطعه کدهای بالا به صورت زیر است.

Can be divided into two subsets of equal sum

پیچیدگی زمانی این روش در بدترین حالت از درجه (O(2ⁿ است. این روش دو احتمال (در نظر گرفتن یا نگرفتن) را برای هر یک از عناصر می‌سنجد.

راهکار برنامه نویسی پویا برای حل مساله تقسیم بندی

این مساله را می‌توان هنگامی که مجموع عناصر خیلی بزرگ نیست، با استفاده از «برنامه‌نویسی پویا» (Dynamic Programming) نیز حل کرد. می‌توان یک آرایه دوبُعدی [][]part با اندازه $$(\frac{sum}{2})*(n+1)$$ ساخت. همچنین، می‌توان راهکار را به صورت پایین به بالا به گونه‌ای ساخت که هر ورودی دارای خصوصیات زیر باشد.

part[i][j] = true if a subset of {arr[0], arr[1], ..arr[j-1]} has sum 
equal to i, otherwise false

حل مساله تقسیم بندی با برنامه‌نویسی پویا در ++C/C

// A Dynamic Programming based C program to partition problem 
#include <stdio.h> 
  
// Returns true if arr[] can be partitioned in two subsets of 
// equal sum, otherwise false 
bool findPartiion (int arr[], int n) 
{ 
    int sum = 0; 
    int i, j; 
    
    // Caculcate sun of all elements 
    for (i = 0; i < n; i++) 
      sum += arr[i]; 
      
    if (sum%2 != 0)   
       return false; 
    
    bool part[sum/2+1][n+1]; 
      
    // initialize top row as true 
    for (i = 0; i <= n; i++) 
      part[0][i] = true; 
        
    // initialize leftmost column, except part[0][0], as 0 
    for (i = 1; i <= sum/2; i++) 
      part[i][0] = false;      
       
     // Fill the partition table in botton up manner  
     for (i = 1; i <= sum/2; i++)   
     { 
       for (j = 1; j <= n; j++)   
       { 
         part[i][j] = part[i][j-1]; 
         if (i >= arr[j-1]) 
           part[i][j] = part[i][j] || part[i - arr[j-1]][j-1]; 
       }         
     }     
       
    /* // uncomment this part to print table  
     for (i = 0; i <= sum/2; i++)   
     { 
       for (j = 0; j <= n; j++)   
          printf ("%4d", part[i][j]); 
       printf("\n"); 
     } */ 
       
     return part[sum/2][n]; 
}      
  
// Driver program to test above funtion 
int main() 
{ 
  int arr[] = {3, 1, 1, 2, 2, 1}; 
  int n = sizeof(arr)/sizeof(arr[0]); 
  if (findPartiion(arr, n) == true) 
     printf("Can be divided into two subsets of equal sum"); 
  else
     printf("Can not be divided into two subsets of equal sum"); 
  getchar(); 
  return 0; 
}

حل مساله تقسیم بندی با برنامه‌نویسی پویا در جاوا

// A dynamic programming based Java program for partition problem 
import java.io.*; 
  
class Partition { 
  
    // Returns true if arr[] can be partitioned in two subsets of 
    // equal sum, otherwise false 
    static boolean findPartition (int arr[], int n) 
    { 
        int sum = 0; 
        int i, j; 
  
        // Caculcate sun of all elements 
        for (i = 0; i < n; i++) 
            sum += arr[i]; 
  
        if (sum%2 != 0) 
            return false; 
  
        boolean part[][]=new boolean[sum/2+1][n+1]; 
  
        // initialize top row as true 
        for (i = 0; i <= n; i++) 
            part[0][i] = true; 
  
        // initialize leftmost column, except part[0][0], as 0 
        for (i = 1; i <= sum/2; i++) 
            part[i][0] = false; 
  
        // Fill the partition table in botton up manner 
        for (i = 1; i <= sum/2; i++) 
        { 
            for (j = 1; j <= n; j++) 
            { 
                part[i][j] = part[i][j-1]; 
                if (i >= arr[j-1]) 
                    part[i][j] = part[i][j] || 
                                 part[i - arr[j-1]][j-1]; 
            } 
        } 
  
        /* // uncomment this part to print table 
        for (i = 0; i <= sum/2; i++) 
        { 
            for (j = 0; j <= n; j++) 
                printf ("%4d", part[i][j]); 
            printf("\n"); 
        } */
  
        return part[sum/2][n]; 
    } 
  
    /*Driver function to check for above function*/
    public static void main (String[] args) 
    { 
        int arr[] = {3, 1, 1, 2, 2,1}; 
        int n = arr.length; 
        if (findPartition(arr, n) == true) 
            System.out.println("Can be divided into two "
                               "subsets of equal sum"); 
        else
            System.out.println("Can not be divided into"
                            " two subsets of equal sum"); 
  
    } 
} 
/* This code is contributed by Devesh Agrawal */

حل مساله تقسیم بندی با برنامه‌نویسی پویا در پایتون ۳

# Dynamic Programming based python  
# program to partition problem 
  
# Returns true if arr[] can be  
# partitioned in two subsets of  
# equal sum, otherwise false 
def findPartition(arr, n): 
    sum = 0
    i, j = 0, 0
      
    # calculate sum of all elements 
    for i in range(n): 
        sum += arr[i] 
      
    if sum % 2 != 0: 
        return false 
      
    part = [[ True for i in range(n + 1)]  
                   for j in range(sum // 2 + 1)] 
      
    # initialize top row as true 
    for i in range(0, n + 1): 
        part[0][i] = True
          
    # intialize leftmost column,  
    # except part[0][0], as 0 
    for i in range(1, sum // 2 + 1): 
        part[i][0] = False
      
    # fill the partition table in 
    # bottom up manner 
    for i in range(1, sum // 2 + 1): 
          
        for j in range(1, n + 1): 
            part[i][j] = part[i][j - 1] 
              
            if i >= arr[j - 1]: 
                part[i][j] = (part[i][j] or 
                              part[i - arr[j - 1]][j - 1]) 
          
    return part[sum // 2][n] 
      
# Driver Code 
arr = [3, 1, 1, 2, 2, 1] 
n = len(arr) 
if findPartition(arr, n) == True: 
    print("Can be divided into two",  
             "subsets of equal sum") 
else: 
    print("Can not be divided into ", 
          "two subsets of equal sum") 
  
# This code is contributed  
# by mohit kumar 29 

حل مساله تقسیم بندی با برنامه‌نویسی پویا در #C

// A dynamic programming based C# program  
// for partition problem 
using System; 
  
class GFG { 
      
    // Returns true if arr[] can be partitioned  
    // in two subsets of equal sum, otherwise  
    // false 
    static bool findPartition (int []arr, int n) 
    { 
          
        int sum = 0; 
        int i, j; 
  
        // Caculcate sun of all elements 
        for (i = 0; i < n; i++) 
            sum += arr[i]; 
  
        if (sum % 2 != 0) 
            return false; 
  
        bool [, ]part=new bool[sum / 2 + 1, n + 1]; 
  
        // initialize top row as true 
        for (i = 0; i <= n; i++) 
            part[0, i] = true; 
  
        // initialize leftmost column, except  
        // part[0][0], as 0 
        for (i = 1; i <= sum/2; i++) 
            part[i, 0] = false; 
  
        // Fill the partition table in botton  
        // up manner 
        for (i = 1; i <= sum/2; i++) 
        { 
            for (j = 1; j <= n; j++) 
            { 
                part[i, j] = part[i, j - 1]; 
                if (i >= arr[j - 1]) 
                    part[i, j] = part[i, j] || 
                    part[i - arr[j - 1],j - 1]; 
            } 
        } 
  
        /* // uncomment this part to print table 
        for (i = 0; i <= sum/2; i++) 
        { 
            for (j = 0; j <= n; j++) 
                printf ("%4d", part[i][j]); 
            printf("\n"); 
        } */
  
        return part[sum / 2, n]; 
    } 
  
    // Driver program to test above funtion 
    public static void Main () 
    { 
        int []arr = {3, 1, 1, 2, 2,1}; 
        int n = arr.Length; 
          
        if (findPartition(arr, n) == true) 
            Console.Write("Can be divided" 
                  + " into two subsets of"
                          + " equal sum"); 
        else
            Console.Write("Can not be " 
               + "divided into two subsets"
                      + " of equal sum"); 
  
    } 
} 
  
// This code is contributed by Sam007.

خروجی قطعه کدهای بالا به صورت زیر است.

Can be divided into two subsets of equal sum

نمودار زیر، مقادیر را در جدول تقسیم‌بندی نشان می‌دهد.

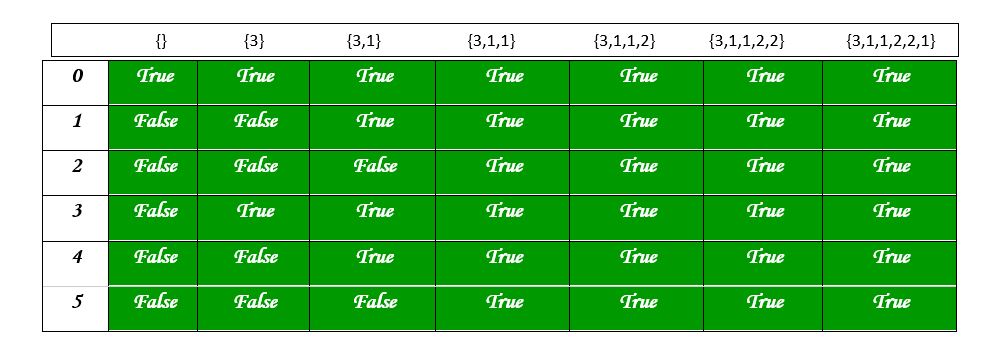
پیچیدگی زمانی این روش از درجه (O(sum*n و فضای کمکی آن از درجه (O(sum*n است. شایان توجه است که این روش برای آرایه‌هایی با مجموع بزرگ قابل استفاده نیست.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده
• الگوریتم جست و جوی دودویی در جاوا اسکریپت — به زبان ساده

^^