بهینه سازی نسبت طلایی – از صفر تا صد (+ دانلود فیلم آموزش رایگان)

بهینه سازی نسبت طلایی یکی از ساده‌ترین الگوریتم‌های ارائه شده در روش‌های بهینه سازی عددی است. در این آموزش قصد داریم به معرفی این الگوریتم بپردازیم.

بهینه سازی علم تعیین بهترین مقادیر برای پارامترها یا متغیرهای یک سیستم، با توجه به یک تابع هزینه مشخص است. مسائل بهینه‌سازی در طول دهه‌های اخیر در اغلب رشته‌ها مانند علوم کامپیوتر و مهندسی تا تحقیق در عملیات و اقتصاد، مورد توجه بسیاری قرار گرفته‌اند. در ساده‌ترین حالت، یک مسئله بهینه‌سازی شامل حداقل‌سازی یا حداکثرسازی یک تابع حقیقی است که ورودی‌های آن در بازه‌ای که مورد بررسی است، انتخاب می‌شوند.

تعمیم این مسئله به سایر مسائل بهینه‌سازی نیازمند حوزه‌های وسیعی از ریاضیات کاربردی است. به صورت کلی هدف از بهینه‌سازی، تعیین بهترین مقدار ممکن برای متغیرهای یک تابع هزینه است که این مقدار باید در داخل یک دامنه تعریف‌ شده از متغیرهای تصمیم باشد. اگر دامنه تعریف متغیرهای تصمیم مشخص نباشد، نوع آن بهینه‌سازی نامقید است که اغلب با استفاده از مفهوم مشتق برای توابع تک‌ متغیره و گرادیان برای توابع چندمتغیره قابل حل هستند. اما اگر دامنه تعریف متغیرهای تصمیم مشخص باشد، به آن بهینه‌سازی مقید گفته می‌شود که عموما ریاضیات آن بسیار پیچیده‌تر از مسائل بهینه‌سازی نامقید است و حتی اغلب حل‌های تحلیلی برای آن وجود ندارد. در این مواقع، تنها امکان تعیین مقادیر بهینه‌ تابع هزینه در ناحیه تعریف‌شده به صورت عددی وجود دارد.

بهینه سازی عددی

منظور از بهینه‌سازی عددی، تکرار یک الگوریتم ساده برای رسیدن به نقطه بهینه در تابع هزینه است. بر خلاف الگوریتم‌های تحلیلی که به صورت مستقیم و کلی، از روی ریشه‌های مشتق یا گرادیان نقطه بهینه را تعیین می‌کنند، در الگوریتم‌های بهینه‌سازی عددی، نقطه بهینه به صورت تکراری و در طی چندمرحله محاسبه می‌شود. الگوریتم‌های بهینه‌سازی عددی، امروزه اهمیت زیادی در علوم مختلف پیدا کرده‌اند و در بهینه‌سازی سیستم‌ها به وفور استفاده می‌شوند.

یک مثال رایج از این کاربردها، شبکه‌های عصبی است که امروزه در کاربردهای متنوعی مانند مدلسازی‌ سیستم‌ها و پیش‌بینی سری‌های زمانی استفاده می‌شوند. در شبکه‌های عصبی، تعداد زیادی پارامتر وجود دارند. این پارامترها باید به صورتی انتخاب شوند که شبکه عصبی همانند سیستم دلخواهی که از قبل مشخص شده است، رفتار کند. به همین دلیل، تابع هزینه مجموع مربعات خطا (بین خروجی سیستم واقعی و شبکه عصبی) تعریف می‌شود و از روی حداقل‌سازی این تابع هزینه، بهترین پارامترهای ممکن برای شبکه عصبی انتخاب می‌شوند. حل تحلیلی با استفاده از گرادیان، به دلیل پیچیدگی بسیار زیاد سیستم، معمولا زمان‌بر است و گاهی اصلا امکان‌پذیر نیست. در نتیجه روش جایگزین، استفاده از الگوریتم‌های بهینه‌سازی عددی است. امروزه در همه شبکه‌های عصبی از الگوریتم‌های بهینه‌سازی عددی برای بهینه‌سازی پارامترهای آن‌ها (که در اصطلاح به آن آموزش شبکه عصبی نیز گفته می‌شود) استفاده می‌کنند.

الگوریتم‌های گسترده‌ای برای بهینه‌سازی عددی وجود دارند که مهمترین آنها عبارتند از: بهینه سازی نسبت طلایی (Golden Section)، الگوریتم گرادیان نزولی (Gradient Descent)، الگوریتم نیوتن، الگوریتم مجموعه فعال (Active-set)، الگوریتم بهینه‌سازی مربعی (Quadratic Optimization) و... . هر کدام از این الگوریتم‌ها برای دسته خاصی از مسائل بهینه‌سازی بهترین عملکرد را دارند و ما باید با توجه به نوع مسئله بهینه‌سازی که می‌خواهیم آن را حل کنیم، بهترین الگوریتم بهینه‌ساز را انتخاب کنیم. در این تحقیق به الگوریتم ساده ولی فوق‌العاده پرکاربرد تقسیم طلایی یا Golden Section می‌پردازیم.

الگوریتم بهینه سازی نسبت طلایی

الگوریتم بهینه سازی نسبت طلایی، بر مبنای عدد طلایی ارائه شده است.‌ فرض کنید که می خواهیم مقدار حداقل تابع $$f(x)$$ در بازه  $$x_{l}$$‌ تا  $$x_{u}$$‌ را به دست آوریم. مطابق شکل زیر ابتدا بازه $$f(x)$$ تا $$x_{u}$$‌ را به صورتی تقسیم می‌کنیم که رابطه زیر برقرار باشد:

$$\frac{{\ell}_1+{\ell}_2}{{\ell}_1}=\frac{{\ell}_1}{{\ell}_1}$$

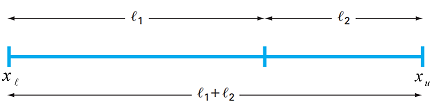
با تعریف متغیر $$\phi=\frac{{\ell}_1}{{\ell}_1}$$، معادله بالا به صورت زیر بازنویسی می‌شود:

$$\phi^{2}-\phi-1=0$$

که جواب قابل قبول این معادله به صورت زیر به دست می‌آید:

$$\phi =\frac{\sqrt{5}+1}{2}=1.61803398874989$$

این عدد همان نسبت طلایی است که قرن‌های متوالی است که به منظور زیباسازی آثار هنری استفاده می‌شود.

یک الگوریتم ساده‌تر برای بهینه‌سازی عددی، استراتژی دوبخشی (همانند الگوریتم دوبخشی در ریشه‌یابی معادلات غیرخطی) است که در آن در هر مرحله، بازه تعریف متغیرهای تصمیم به دو قسمت مساوی تقسیم می‌شود. سپس مقدار تابع هزینه در وسط بازه را با مقادیر ابتدا و انتهای آن مقایسه کرده و به این ترتیب بازه جدیدی به دست می‌آید. بعد از چندین تکرار، طول بازه آن قدر کوچک می‌شود که ابتدا و انتهای آن تقریب متغیرهای تصمیم بهینه هستند. اما در الگوریتم بهینه‌سازی عددی به روش تقسیم طلایی، بازه متغیرهای تصمیم بر اساس عدد طلایی تقسیم‌بندی می‌شود که این امر منجر به افزایش سرعت همگرایی خواهد شد. به عبارت دیگر با تعداد تکرارهای کمتر به نقطه بهینه خواهیم رسید.

در گام اول، الگوریتم بهینه سازی نسبت طلایی پارامتر $$d$$‌ بصورت زیر تعریف می‌شود:

$$d=(\phi-1)(x_{u}-x_{\ell})$$

سپس نقاط $$x_{1}$$  و $$x_{2}$$ بصورت زیر درنظر گرفته می‌شوند:

$$x_{1}=x_{\ell}+d$$

$$x_{2}=x_{u}-d$$

حال برای مسئله حداقل‌سازی تابع هزینه $$f(x)$$‌، با استفاده از دو حالت زیر بازه جدیدی حاصل می‌شود.

حالت اول: مطابق شکل زیر، فرض کنید که $$f(x_{1})$$ باشد. در این شرایط می‌توان نتیجه گرفت که نقطه بهینه در اطراف نقطه $$x_{1}$$، اما دور از نقطه $$x_{2}$$‌ قرار دارد. بنابراین می‌توان گفت که نقطه بهینه در بازه $$x_{2}$$ تا $$x_{u}$$  قرار دارد. پس کران بالای بازه متغیر تصمیم حذف می‌شود ولی کران پایین آن با $$x_{2}$$  جایگزین می‌شود.

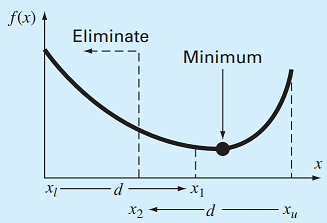
حالت دوم: فرض کنید که $$f(x_{2})$$ باشد. در این شرایط می‌توان نتیجه گرفت که نقطه بهینه در اطراف نقطه $$x_{2}$$، اما دور از نقطه $$x_{1}$$‌ قرار دارد. بنابراین می‌توان گفت که نقطه بهینه در بازه $$x_{\ell}$$ تا $$x_{2}$$  قرار دارد. پس کران پایین بازه متغیر تصمیم حذف می‌شود ولی کران بالای آن با $$x_{1}$$ جایگزین می‌شود.

در حالت کلی با قرینه کردن تابع هزینه می‌توان مسئله حداکثرسازی را به حداقل‌سازی تبدیل کرد. زیرا نقاط مینیمم یک تابع بیانگر نقاط ماکزیمم قرینه تابع نیز خواهند بود. همچنین نقاط حداکثر یک تابع بیانگر نقاط مینیمم قرینه آن نیز هستند. پس می‌توان در حالت کلی از الگوریتم حداقل‌سازی استفاده کرد و مسئله حداکثرسازی را با قرینه کردن تابع هزینه آن به مسئله حداقل‌سازی تبدیل کرد.

حل مسئله

برای مثال فرض کنید که می‌خواهیم مقدار حداقل تابع زیر را در بازه 0 تا 4 بدست آوریم:

$$f(x)=0.1x^{2}-2sin(x)$$

فیلم آموزش شبیه سازی سری فیبوناچی و محاسبه عدد طلایی در سیمیولینک (رایگان) در فرادرس

کلیک کنید

در گام اول،  $$x_{\ell}=0$$ و $$x_{u}=4$$ است. بنابراین مقادیر $$d$$، $$x_{1}$$ و $$x_{۲}$$ به صورت زیر بدست می‌آیند:

$$d=(1.61803-1)(4-0)=2.4721$$

$$x_{1}=0+2.4721=2.4721$$

$$x_{2}=4-2.4721=1.5279$$

حال مقادیر تابع هزینه یا همان تابع $$f(x)$$ را در این نقاط محاسبه می‌کنیم:

$$f(x_{2})=0.1(1.5279)^{2}-2sin(1.5279)=-1.7647$$

$$f(x_{1})=0.1(2.4721)^{2}-2sin(2.4721)=-0.6300$$

واضح است که $$f(x_{2})$$. پس می‌توان گفت نقطه بهینه در اطراف $$x_{2}$$ قرار دارد. پس طبق حالت دوم، کران بالای بازه تغییر پیدا می‌کند و بازه جدید برابر با 0 تا 2.4721 خواهد بود. حال مراحل قبل را با درنظر گرفتن بازه جدید تکرار می‌کنیم.

در گام دوم، $$x_{\ell}=0$$‌ و $$x_{u}=2.4721$$ است. با این اعداد جدید، مقادیر $$d$$، $$x_{1}$$ و $$x_{2}$$ به صورت زیر به دست می‌آیند:

$$d=(1.61803-1)(2.4721-0)=1.5279$$

$$x_{1}=0+1.5279=1.5279$$

$$x_{2}=2.4721-1.5279=0.9443$$

حال مقادیر تابع هزینه یا همان تابع $$f(x)$$ را در این نقاط محاسبه می‌کنیم:

$$f(x_{2})=0.1(0.9443)^{2}-2sin(0.9443)=-1.5310$$

$$f(x_{1})=0.1(1.5279)^{2}-2sin(1.5279)=-1.7647$$

واضح است که $$f(x_{1})$$. پس می‌توان گفت نقطه بهینه در اطراف $$x_{1}$$ قرار دارد. پس طبق حالت اول کران پایین بازه تغییر پیدا می‌کند و بازه جدید 0.9443 تا 2.4721 خواهد بود. حال دوباره مراحل قبل را با درنظر گرفتن بازه جدید تکرار می‌کنیم.‌

بقیه مراحل سرراست و واضح است. در جدول زیر نتایج 8 تکرار اول الگوریتم نشان داده شده است:

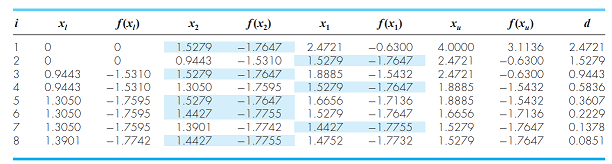
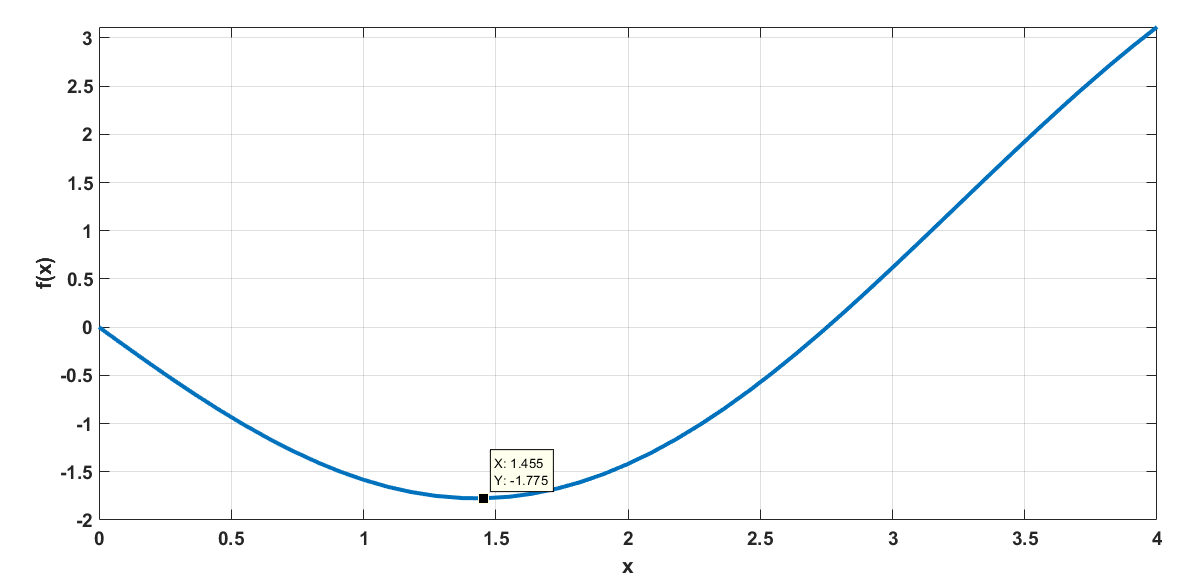
همان طور که از روی جدول بالا مشخص است با هر بار اجرای الگوریتم بازه تعریف متغیرهای تصمیم کوچکتر خواهد شد و در نهایت این بازه به نقطه‌ای همگرا خواهد شد که تابع در آن نقطه دارای حداقل مقدار (در بازه 0 تا 4) است. شکل زیر نمودار تابع در بازه 0 تا 4 را نشان می‌دهد. مشخص است که نقطه بهینه 1.455 است که طبق جدول بالا مقادیر $$x_{1}$$‌ و $$x_{2}$$ تمایل دارند به سمت این نقطه همگرا شوند.

برنامه متلب زیر با استفاده از الگوریتم بهینه سازی نسبت طلایی نقطه مینیمم تابع را محاسبه می‌کند.

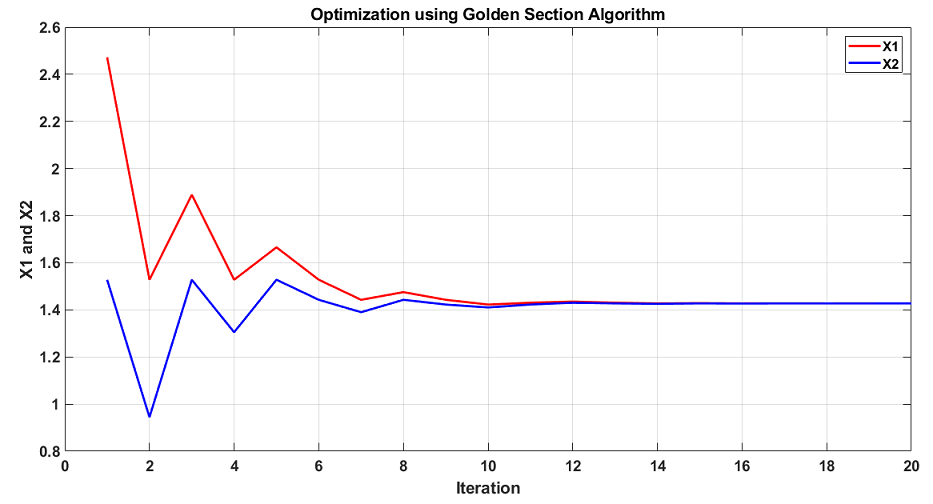
بعد از اجرای برنامه مطابق شکل زیر نمودار همگرایی الگوریتم رسم می‌شود. طبق این نمودار واضح است که بعد از 14 تکرار مقادیر $$x_{1}$$‌ و $$x_{2}$$ به  1.427 همگرا شده اند که نقطه بهینه تحلیلی تابع را نشان می‌دهد.

اگر مطلب بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های محاسبات عددی
• آموزش محاسبات عددی با MATLAB
• مجموعه آموزش‌های الگوریتم‌‌های بهینه‌‌سازی هوشمند
• آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون (Python)
• کاربرد بهینه‌سازی در هندسه — به زبان ساده
• مسائل بهینه سازی در فیزیک — به زبان ساده

^^