گاهی در محاسبات لازم است توابعی از ماتریسها را محاسبه کنیم. اما انجام این کار به صورت مستقیم، دشوار و مستلزم محاسبات فراوانی است. در این موارد، قضیه «کیلی همیلتون» (Cayley-Hamilton Theorem) محاسبات را سادهتر خواهد کرد. به بیان ساده، قضیه کیلی همیلتون بیان میکند که هر ماتریس مربعی در معادله مشخصه خود صدق میکند. از این ویژگی میتوان استفادههای فراوانی کرد. در این آموزش، قضیه کیلی-همیلتون را بیان کرده و چند مثال مربوط به آن را بررسی میکنیم.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
قضیه کیلی همیلتون
اگر چندجملهای p ( λ ) p ( \lambda) p ( λ ) چندجملهای مشخصه ماتریس A A A n × n n \times n n × n p ( A ) p ( A ) p ( A ) n × n n \times n n × n A A A
اثبات قضیه کیلی همیلتون
فرض کنید A A A n × n n \times n n × n A i , j A_{i,j} A i , j i i i j j j A A A ماتریس الحاقی $$A_{\mbox{adj}}=[(-1)^{i+j}A_{j,i}] $$
$$ \large A A _ { \mbox {adj} } = A _ { \mbox {adj} } A = \mbox {det} ( A ) I , $$
که در آن، $$\mbox{det}(A) $$
رابطه زیر نیز برقرار است:
$$ \large ( A - \lambda I ) ( A - \lambda I ) _ { \mbox{adj} } = ( A - \lambda I ) _ { \mbox {adj} } ( A - \lambda I ) =<br />
\mbox {det} ( A - \lambda I ) I $$
ماتریس $$(A-\lambda I)_{\mbox{adj}} $$
$$ \large ( A - \lambda I ) _ { \mbox {adj} } = Q _ { 0 } + \lambda Q _ { 1 } + \cdots + \lambda ^ { n - 1 } Q _ { n - 1 } , $$
که در آن، Q j Q_{j} Q j n × n n \times n n × n
( Q 0 + Q 1 λ + ⋯ + Q n − 1 λ n − 1 ) ( A − λ I ) = p ( λ ) I , \large ( Q _ { 0 } + Q _ { 1 } \lambda + \cdots + Q _ { n - 1 } \lambda ^ { n - 1 } ) ( A - \lambda I ) = p ( \lambda ) I , ( Q 0 + Q 1 λ + ⋯ + Q n − 1 λ n − 1 ) ( A − λ I ) = p ( λ ) I ,
که در آن، $$ p(\lambda)=\mbox{det}(\lambda I -A) $$
p ( λ ) = α 0 + α 1 λ + ⋯ + α n − 1 λ n − 1 + λ n \large p ( \lambda ) = \alpha _ 0 + \alpha _ 1 \lambda + \cdots + \alpha _ { n - 1 } \lambda ^ { n - 1 } + \lambda ^ n p ( λ ) = α 0 + α 1 λ + ⋯ + α n − 1 λ n − 1 + λ n
با برابر قرار دادن ضرایب λ \lambda λ I I I A A A ⋯ \cdots ⋯ A n A^n A n
− A Q 0 = α 0 I → I × → − A Q 0 = α 0 I Q 0 − A Q 1 = α 1 I → A × → A Q 0 − A 2 Q 1 = α 1 A Q 1 − A Q 2 = α 2 I → A 2 × → A 2 Q 1 − A 3 Q 2 = α 2 A ⋮ ⋮ ⋮ Q n − 2 − A Q n − 1 = α n − 1 I → A n − 1 × → A n − 1 Q n − 2 − A n Q n − 1 = α n − 1 A n − 1 Q n − 1 = I → A n × → A n Q n − 1 = A n \large \begin{matrix} - A Q _ 0 = \alpha _ 0 I & \rightarrow I \times \rightarrow & - AQ_0=\alpha _0 I \\ Q _0 -AQ _ 1 = \alpha _ 1 I & \rightarrow A \times \rightarrow & A Q _ 0 - A ^ 2 Q _ 1 = \alpha _ 1 A \\ Q _1 -AQ _ 2 = \alpha _ 2 I & \rightarrow A ^ 2 \times \rightarrow & A^ 2 Q _ 1 - A ^ 3 Q _ 2 = \alpha _ 2 A \\ \vdots & \vdots & \vdots \\ Q _ { n -2 } - A Q _ {n -1 } = \alpha _ {n-1 } I & \rightarrow A ^ {n-1} \times \rightarrow & A ^ { n -1 } Q _ { n-2} - A ^ n Q _ {n-1} = \alpha _ { n-1} A ^ {n-1} \\ Q _ { n -1 } = I & \rightarrow A ^ {n} \times \rightarrow & A ^ { n } Q _ { n-1} = A ^ {n} \end {matrix} − A Q 0 = α 0 I Q 0 − A Q 1 = α 1 I Q 1 − A Q 2 = α 2 I ⋮ Q n − 2 − A Q n − 1 = α n − 1 I Q n − 1 = I → I × → → A × → → A 2 × → ⋮ → A n − 1 × → → A n × → − A Q 0 = α 0 I A Q 0 − A 2 Q 1 = α 1 A A 2 Q 1 − A 3 Q 2 = α 2 A ⋮ A n − 1 Q n − 2 − A n Q n − 1 = α n − 1 A n − 1 A n Q n − 1 = A n
حال معادلات سمت راست را با یکدیگر جمع میکنیم و در نهایت، داریم:
O = α 0 I + α 1 A + ⋯ + α n − 1 A n − 1 + A n \large O = \alpha _ 0 I + \alpha _ 1 A + \cdots + \alpha _ { n -1 } A ^ { n-1} + A ^n O = α 0 I + α 1 A + ⋯ + α n − 1 A n − 1 + A n
مثالها
در ادامه، چند مثال را از کاربرد قضیه کیلی-همیلتون بررسی میکنیم.
مثال ۱
ماتریس A A A
A = [ 1 1 1 3 ] \large A = \begin {bmatrix} 1 & 1 \\ 1 & 3 \end {bmatrix} A = [ 1 1 1 3 ]
چندجملهای مشخصه p ( t ) p ( t) p ( t ) A A A
p ( t ) = det ( A − t I ) = [ 1 − t 1 1 3 − t ] = t 2 − 4 t + 2. \large \begin {align*} p ( t ) & = \det ( A - t I ) = \begin {bmatrix} 1 - t & 1 \\ 1 & 3 - t \end {bmatrix} \\ & = t ^ 2 - 4 t + 2 . \end {align*} p ( t ) = det ( A − t I ) = [ 1 − t 1 1 3 − t ] = t 2 − 4 t + 2.
طبق قضیه کیلی-همیلتون، ماتریس p ( A ) = A 2 − 4 A + 2 I p ( A ) = A ^ 2 - 4 A + 2 I p ( A ) = A 2 − 4 A + 2 I 2 × 2 2 \times 2 2 × 2
p ( A ) = A 2 − 4 A + 2 I = [ 1 1 1 3 ] [ 1 1 1 3 ] − 4 [ 1 1 1 3 ] + 2 [ 1 0 0 1 ] = [ 2 4 4 10 ] + [ − 4 − 4 − 4 − 12 ] + [ 2 0 0 2 ] = [ 0 0 0 0 ] . \large \begin {align*} p ( A ) & = A ^ 2 - 4 A + 2 I = \begin {bmatrix} 1 & 1 \\ 1 & 3 \end {bmatrix} \begin {bmatrix} 1 & 1 \\ 1 & 3 \end {bmatrix} - 4 \begin {bmatrix} 1 & 1 \\ 1& 3 \end {bmatrix} + 2 \begin {bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix} \\[6pt] & = \begin {bmatrix} 2 & 4 \\ 4 & 10 \end {bmatrix} + \begin {bmatrix} - 4 & - 4 \\ - 4 & - 1 2 \end {bmatrix} +\begin {bmatrix} 2 & 0 \\ 0 & 2 \end {bmatrix} = \begin {bmatrix} 0 & 0 \\ 0 & 0 \end {bmatrix}. \end {align*} p ( A ) = A 2 − 4 A + 2 I = [ 1 1 1 3 ] [ 1 1 1 3 ] − 4 [ 1 1 1 3 ] + 2 [ 1 0 0 1 ] = [ 2 4 4 10 ] + [ − 4 − 4 − 4 − 12 ] + [ 2 0 0 2 ] = [ 0 0 0 0 ] .
مثال ۲
ماتریس زیر را در نظر بگیرید.
T = [ 1 0 2 0 1 1 0 0 2 ] \large T = \begin {bmatrix} 1 & 0 & 2 \\ 0 & 1 & 1 \\ 0 & 0 & 2 \end {bmatrix} T = 1 0 0 0 1 0 2 1 2
عبارت − T 3 + 4 T 2 + 5 T − 2 I -T^3+4T^2+5T-2I − T 3 + 4 T 2 + 5 T − 2 I I I I 3 × 3 3 \times 3 3 × 3
حل: از قضیه کیلی-همیلتون استفاده میکنیم. برای به دست آوردن چندجملهای مشخصه T T T T − t I T - t I T − t I دترمینان یک ماتریس بالامثلثی برابر با حاصلضرب درایههای قطری آن است. بنابراین، چندجملهای مشخصه p T ( t ) p_T(t) p T ( t ) T T T
p T ( t ) = det ( T − t I ) = ( 1 − t ) ( 1 − t ) ( 2 − t ) = − t 3 + 4 t 2 − 5 t + 2. \large p _ T ( t ) = \det ( T - t I ) = ( 1 - t ) ( 1 - t ) ( 2 - t ) = - t ^ 3 + 4 t ^ 2 - 5 t + 2 . p T ( t ) = det ( T − t I ) = ( 1 − t ) ( 1 − t ) ( 2 − t ) = − t 3 + 4 t 2 − 5 t + 2.
با توجه به قضیه کیلی-همیلتون، داریم:
p T ( T ) = − T 3 + 4 T 2 − 5 T + 2 I = O . \large p _ T ( T ) = - T ^ 3 + 4 T ^ 2 -5 T + 2 I = O . p T ( T ) = − T 3 + 4 T 2 − 5 T + 2 I = O .
که در آن، O O O 3 × 3 3 \times 3 3 × 3
حاصل عبارت فوق، برابر است با:
− T 3 + 4 T 2 + 5 T − 2 I = ( − T 3 + 4 T 2 − 5 T + 2 I ) + ( 10 T − 4 I ) = p T ( T ) + 10 T − 4 I = 10 T − 4 I = [ 10 0 20 0 10 10 0 0 20 ] – [ 4 0 0 0 4 0 0 0 4 ] = [ 6 0 20 0 6 10 0 0 16 ] . \large \begin {align*} - T ^ 3 + 4 T ^ 2 + 5 T - 2 I & = ( - T ^ 3 + 4 T ^ 2 - 5 T + 2 I ) + ( 1 0 T - 4 I ) \\ & = p _ T ( T ) + 1 0 T - 4 I = 1 0 T - 4 I \\[6pt] & = \begin {bmatrix} 10 & 0 & 20 \\ 0 &10 &10 \\ 0 & 0 & 20 \end {bmatrix} – \begin {bmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \end {bmatrix} \\[6pt] & = \begin {bmatrix} 6 & 0 & 20 \\ 0 & 6 &10 \\ 0 & 0 & 16 \end {bmatrix} . \end {align*} − T 3 + 4 T 2 + 5 T − 2 I = ( − T 3 + 4 T 2 − 5 T + 2 I ) + ( 10 T − 4 I ) = p T ( T ) + 10 T − 4 I = 10 T − 4 I = 10 0 0 0 10 0 20 10 20 – 4 0 0 0 4 0 0 0 4 = 6 0 0 0 6 0 20 10 16 .
بنابراین، پاسخ این مثال برابر است با:
− T 3 + 4 T 2 + 5 T − 2 I = [ 6 0 20 0 6 10 0 0 16 ] . \large - T ^ 3 + 4 T ^ 2 + 5 T - 2 I = \begin {bmatrix} 6 & 0 & 20 \\ 0 & 6 & 10 \\ 0 & 0 & 16 \end {bmatrix} . − T 3 + 4 T 2 + 5 T − 2 I = 6 0 0 0 6 0 20 10 16 .
مثال ۳
با استفاده از قضیه کیلی-همیلتون معمکوس ماتریس زیر را محاسبه کنید.
A = [ 1 1 2 9 2 0 5 0 3 ] \large A = \begin {bmatrix} 1 & 1 & 2 \\ 9 & 2 & 0 \\ 5 & 0 & 3 \end {bmatrix} A = 1 9 5 1 2 0 2 0 3
حل: برای استفاده از قضیه کیلی-همیلتون، ابتدا چندجملهای مشخصه p ( t ) p ( t) p ( t ) A A A
p ( t ) = det ( A − t I ) = ∣ 1 − t 1 2 9 2 − t 0 5 0 3 − t ∣ = ( − 1 ) 3 + 1 5 ∣ 1 2 2 − t 0 ∣ + ( − 1 ) 3 + 2 ⋅ 0 ∣ 1 − t 2 9 0 ∣ + ( − 1 ) 3 + 3 ( 3 − t ) ∣ 1 − t 1 9 2 − t ∣ = 5 ( 2 t − 4 ) + 0 + ( 3 − t ) ( ( 1 − t ) ( 2 − t ) − 9 ) = − t 3 + 6 t 2 + 8 t − 41. \large \begin {align*} p ( t ) & = \det ( A - t I ) = \begin {vmatrix} 1 - t & 1 & 2 \\ 9 & 2 - t & 0 \\ 5 & 0 & 3 - t \end {vmatrix} \\[6pt] & = ( - 1 ) ^ { 3 + 1 } 5 \begin {vmatrix} 1 & 2 \\ 2 - t & 0 \end {vmatrix} + ( - 1 ) ^ { 3 + 2 } \cdot 0 \begin {vmatrix} 1 - t & 2\\ 9 & 0 \end {vmatrix} + ( - 1 ) ^ { 3 + 3 } ( 3 - t ) \begin {vmatrix} 1- t & 1 \\ 9 & 2 - t \end {vmatrix} \\[6pt] & = 5 ( 2 t - 4 ) + 0 + ( 3 - t ) \left( \, ( 1 - t ) ( 2 - t ) - 9 \, \right) \\ & = - t ^ 3 + 6 t ^ 2 + 8 t - 4 1 . \end {align*} p ( t ) = det ( A − t I ) = 1 − t 9 5 1 2 − t 0 2 0 3 − t = ( − 1 ) 3 + 1 5 1 2 − t 2 0 + ( − 1 ) 3 + 2 ⋅ 0 1 − t 9 2 0 + ( − 1 ) 3 + 3 ( 3 − t ) 1 − t 9 1 2 − t = 5 ( 2 t − 4 ) + 0 + ( 3 − t ) ( ( 1 − t ) ( 2 − t ) − 9 ) = − t 3 + 6 t 2 + 8 t − 41.
طبق قضیه کیلی-همیلتون، رابطه p ( A ) = O p(A)=O p ( A ) = O
O = p ( A ) = − A 3 + 6 A 2 + 8 A − 41 I . \large \begin {align*} O = p ( A ) = - A ^ 3 + 6 A ^ 2 + 8 A -4 1 I . \end {align*} O = p ( A ) = − A 3 + 6 A 2 + 8 A − 41 I .
بنابراین، داریم:
41 I = − A 3 + 6 A 2 + 8 A = A ( − A 2 + 6 A + 8 I ) , \large 4 1 I = - A ^ 3 + 6 A ^ 2 + 8 A = A ( - A ^ 2 + 6 A + 8 I ) , 41 I = − A 3 + 6 A 2 + 8 A = A ( − A 2 + 6 A + 8 I ) ,
یا به طور معادل:
I = A ( 1 41 ( − A 2 + 6 A + 8 I ) ) . \large I = A \left( \, \frac { 1 } { 4 1 } ( -A ^ 2 + 6 A + 8 I ) \, \right) . I = A ( 41 1 ( − A 2 + 6 A + 8 I ) ) .
بنابراین، معکوس ماتریس را میتوان با استفاده از فرمول زیر به دست آورد:
A − 1 = 1 41 ( − A 2 + 6 A + 8 I ) . \large A ^ { - 1 } = \frac { 1 } { 4 1 } ( - A^ 2 + 6 A + 8 I ) . A − 1 = 41 1 ( − A 2 + 6 A + 8 I ) .
ماتریس A 2 A ^ 2 A 2
A 2 = [ 20 3 8 27 13 18 20 5 19 ] \large A ^ 2 = \begin {bmatrix} 20 & 3 & 8 \\ 27 & 13 & 18 \\ 20 & 5 & 19 \end {bmatrix} A 2 = 20 27 20 3 13 5 8 18 19
و
− A 2 + 6 A + 8 I = − [ 20 3 8 27 13 18 20 5 19 ] + 6 [ 1 1 2 9 2 0 5 0 3 ] + 8 [ 1 0 0 0 1 0 0 0 1 ] = [ − 6 3 4 27 7 − 18 10 − 5 7 ] . \large \begin {align*} - A ^ 2 + 6 A + 8 I & = - \begin {bmatrix} 20 & 3 & 8 \\ 27 & 13 & 18 \\ 20 & 5 & 19 \end {bmatrix} + 6 \begin {bmatrix} 1 & 1 & 2 \\ 9 & 2 & 0 \\ 5 & 0 & 3 \end {bmatrix} + 8 \begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end {bmatrix} \\[6pt] & = \begin {bmatrix} -6 & 3 & 4 \\ 27 & 7 & -18 \\ 10 & -5 & 7 \end {bmatrix}. \end {align*} − A 2 + 6 A + 8 I = − 20 27 20 3 13 5 8 18 19 + 6 1 9 5 1 2 0 2 0 3 + 8 1 0 0 0 1 0 0 0 1 = − 6 27 10 3 7 − 5 4 − 18 7 .
در نتیجه، معکوس ماتریس A A A
A − 1 = 1 41 [ − 6 3 4 27 7 − 18 10 − 5 7 ] . \large A ^ { - 1 } = \frac { 1 } { 4 1 } \begin {bmatrix} -6 & 3 & 4 \\ 27 & 7 & -18 \\ 10 & -5 & 7 \end {bmatrix} . A − 1 = 41 1 − 6 27 10 3 7 − 5 4 − 18 7 .
مثال 4
ماتریس زیر را در نظر بگیرید:
A = [ 1 − 1 2 3 ] . \large A = \begin {bmatrix} 1 & - 1 \\ 2 & 3 \end {bmatrix} . A = [ 1 2 − 1 3 ] .
مقادیر ویژه و بردارهای ویژه ماتریس زیر را محاسبه کنید.
B = A 4 − 3 A 3 + 3 A 2 − 2 A + 8 I . \large B = A ^ 4 - 3 A ^ 3 + 3 A ^ 2 - 2 A + 8 I . B = A 4 − 3 A 3 + 3 A 2 − 2 A + 8 I .
I I I
حل: ابتدا چندجملهای مشخصه p A ( t ) p_A(t) p A ( t ) A A A
p A ( t ) = det ( A − t I ) = ∣ 1 − t − 1 2 3 − t ∣ = ( 1 − t ) ( 3 − t ) − ( − 1 ) ( 2 ) = t 2 − 4 t + 5. \large \begin {align*} p _ A ( t ) & = \det ( A - t I ) = \begin {vmatrix} 1 - t & - 1 \\ 2 & 3 - t \end {vmatrix} \\ & = ( 1 - t ) ( 3 - t ) - ( - 1 ) ( 2 ) = t ^ 2 - 4 t + 5 . \end {align*} p A ( t ) = det ( A − t I ) = 1 − t 2 − 1 3 − t = ( 1 − t ) ( 3 − t ) − ( − 1 ) ( 2 ) = t 2 − 4 t + 5.
با حل t 2 − 4 t + 5 = 0 t^2-4t+5=0 t 2 − 4 t + 5 = 0 A A A 2 ± i 2\pm i 2 ± i B B B
برای سادگی محاسبه، از قضیه کیلی-همیلتون استفاده میکنیم:
p t ( A ) = A 2 − 4 A + 5 I = O , \large p _ t ( A ) = A ^ 2 - 4 A + 5 I = O , p t ( A ) = A 2 − 4 A + 5 I = O ,
که در آن، I I I 2 × 2 2 \times 2 2 × 2 O O O 2 × 2 2 \times 2 2 × 2
بنابراین، داریم:
B = A 4 − 3 A 3 + 3 A 2 − 2 A + 8 I = ( A 2 − 4 A + 5 I ) ( A 2 + A + 2 I ) + A − 2 I , \large B = A ^ 4 - 3 A ^ 3 + 3 A ^ 2 - 2 A + 8 I = ( A ^2 - 4 A + 5 I ) ( A ^ 2 + A + 2 I ) + A - 2 I , B = A 4 − 3 A 3 + 3 A 2 − 2 A + 8 I = ( A 2 − 4 A + 5 I ) ( A 2 + A + 2 I ) + A − 2 I ,
و در نتیجه:
B = A − 2 I = [ − 1 − 1 2 1 ] . \large B = A - 2 I = \begin {bmatrix} - 1 & - 1 \\ 2 & 1 \end {bmatrix} . B = A − 2 I = [ − 1 2 − 1 1 ] .
از آنجایی که مقادیر ویژه ماتریس A A A 2 ± i 2\pm i 2 ± i B = A − 2 I B=A-2I B = A − 2 I
( 2 ± i ) − 2 = ± i . \large ( 2 \pm i ) - 2 = \pm i . ( 2 ± i ) − 2 = ± i .
در ادامه، بردار ویژهها را به دست میآوریم. ابتدا بردار ویژه متناظر با مقدار ویژه i i i
A − i I = [ − 1 − i − 1 2 1 − i ] → ( − 1 + i ) R 1 [ 2 1 − i 2 1 − i ] → R 2 − R 1 [ 2 1 − i 0 0 ] → 1 2 R 1 [ 1 ( 1 − i ) / 2 0 0 ] . \large \begin {align*} A - i I & = \begin {bmatrix} - 1 - i & - 1 \\ 2 & 1 - i \end {bmatrix} \xrightarrow { ( - 1 + i ) R _ 1 } \begin {bmatrix} 2 & 1 - i \\ 2 & 1 - i \end {bmatrix} \\ & \xrightarrow { R _ 2 - R _ 1 } \begin {bmatrix} 2 & 1 - i \\ 0 & 0 \end {bmatrix} \xrightarrow { \frac { 1 } { 2} R _ 1 } \begin {bmatrix} 1 & ( 1 - i ) / 2 \\ 0 & 0 \end {bmatrix} . \end {align*} A − i I = [ − 1 − i 2 − 1 1 − i ] ( − 1 + i ) R 1 [ 2 2 1 − i 1 − i ] R 2 − R 1 [ 2 0 1 − i 0 ] 2 1 R 1 [ 1 0 ( 1 − i ) /2 0 ] .
بنابراین، داریم:
x 1 = − 1 − i 2 \large x _ 1 = - \frac { 1 - i } { 2 } x 1 = − 2 1 − i
و بردارهای ویژه متناظر با مقدار ویژه i i i
x = x 2 [ − 1 − i 2 1 ] , \large \mathbf { x } = x _ 2 \begin {bmatrix} - \frac { 1 - i } { 2 } \\ 1 \end {bmatrix} , x = x 2 [ − 2 1 − i 1 ] ,
که در آن، x 2 x _ 2 x 2 عدد مختلط غیرصفری میتواند باشد.
اگر از − 1 + i -1+i − 1 + i i i i
a [ 1 − 1 − i ] \large a\begin{bmatrix} 1 \\ -1-i \end{bmatrix} a [ 1 − 1 − i ]
که در آن، a a a
از آنجایی که B B B i i i − i -i − i مزدوج مختلط یکدیگر هستند، بردار ویژههای متناظر با مقدار ویژه − i -i − i
b [ 1 − 1 + i ] , \large b \begin {bmatrix} 1 \\ - 1 + i \end {bmatrix} , b [ 1 − 1 + i ] ,
که در آن، b b b
مثال ۵
فرض کنید A A A B B B 2 × 2 2 \times 2 2 × 2 A = A B − B A A=AB-BA A = A B − B A A 2 = O A ^ 2 = O A 2 = O O O O 2 × 2 2 \times 2 2 × 2
حل: برای اثبات رابطه مورد نظر، ابتدا اثر ماتریس A A A
اثر ماتریس A A A
tr ( A ) = tr ( A B − B A ) = tr ( A B ) − tr ( B A ) = tr ( A B ) − tr ( A B ) = 0. \large \begin {align*} \text {tr} ( A ) & = \text {tr} ( A B - B A)\\ &=\text {tr}(AB)-\text {tr}(BA)\\ &=\text {tr}(AB)-\text {tr}(AB)=0. \end{align*} tr ( A ) = tr ( A B − B A ) = tr ( A B ) − tr ( B A ) = tr ( A B ) − tr ( A B ) = 0.
بنابراین، tr ( A ) = 0 \text{tr} (A) = 0 tr ( A ) = 0
O = A 2 − tr ( A ) A + det ( A ) I = A 2 + det ( A ) I , \large \begin {align*} O & = A ^ 2 - \text{tr} ( A ) A + \det ( A ) I \\ & = A ^ 2 + \det ( A ) I , \end{align*} O = A 2 − tr ( A ) A + det ( A ) I = A 2 + det ( A ) I ,
که در آن، I I I 2 × 2 2 \times 2 2 × 2
از رابطه اخیر، داریم:
A 2 = − det ( A ) I . ( ∗ ) \large A ^ 2 = - \det ( A ) I . \; \; \; \; \; \; \; \; {(*)} A 2 = − det ( A ) I . ( ∗ )
در ادامه، ماتریس A 2 A ^ 2 A 2
A 2 = A ( A B − B A ) = A 2 B − A B A \large \begin {align*} A ^ 2 = A ( A B - B A ) = A ^ 2 B - A B A \end {align*} A 2 = A ( A B − B A ) = A 2 B − A B A
و
A 2 = ( A B − B A ) A = A B A − B A 2 . \large \begin {align*} A ^ 2 = ( A B - B A ) A = A B A - B A ^ 2 . \end{align*} A 2 = ( A B − B A ) A = A B A − B A 2 .
با جمع دو معادله اخیر با یکدیگر، عبارت زیر به دست میآید:
2 A 2 = A 2 B − B A 2 = ( ∗ ) ( − det ( A ) I ) B − B ( − det ( A ) I ) = − det ( A ) B + det ( A ) B = O . \large \begin {align*} 2 A ^ 2 & = A ^ 2 B - B A ^ 2 \\ & \stackrel { ( * ) } { = } ( - \det ( A ) I ) B - B ( - \det ( A ) I ) \\ & = - \det ( A ) B + \det ( A ) B = O . \end {align*} 2 A 2 = A 2 B − B A 2 = ( ∗ ) ( − det ( A ) I ) B − B ( − det ( A ) I ) = − det ( A ) B + det ( A ) B = O .
در نتیجه، میبینیم که رابطه A 2 = O A^2=O A 2 = O
قضیه کیلی-همیلتون برای یک ماتریس 2 × 2 2 \times 2 2 × 2
فرض کنید A = [ a b c d ] A=\begin{bmatrix} a & b\\ c& d \end{bmatrix} A = [ a c b d ] 2 × 2 2 \times 2 2 × 2
چندجملهای مشخصه برابر است با:
p ( x ) = det ( A − x I ) = ∣ a − x b c d − x ∣ = ( a − x ) ( d − x ) − b c = x 2 − ( a + d ) x + a d − b c = x 2 − tr ( A ) x + det ( A ) , \large \begin {align*} p ( x ) & = \det ( A - x I ) \\ & = \begin {vmatrix} a - x & b \\ c & d - x \end {vmatrix}\\ & = ( a - x ) ( d - x ) - b c \\ & = x ^ 2 - ( a + d ) x + a d - b c \\ & = x ^ 2 -\text {tr} ( A ) x + \det ( A ) , \end {align*} p ( x ) = det ( A − x I ) = a − x c b d − x = ( a − x ) ( d − x ) − b c = x 2 − ( a + d ) x + a d − b c = x 2 − tr ( A ) x + det ( A ) ,
که tr ( A ) = a + d \text{tr} ( A ) = a + d tr ( A ) = a + d det ( A ) = a d − b c \det(A)=ad-bc det ( A ) = a d − b c
قضیه کیلی-همیلتون بیان میکند که ماتریس A A A p ( x ) = 0 p ( x ) = 0 p ( x ) = 0
A 2 − tr ( A ) A + det ( A ) I = O . \large A ^ 2 - \text {tr} ( A ) A + \det ( A ) I = O . A 2 − tr ( A ) A + det ( A ) I = O .
مثال ۶
در کدام یک از موارد زیر ماتریس A A A A − 1 A ^ { -1} A − 1 A A A A A A
(الف) A A A 3 × 3 3 \times 3 3 × 3 λ = i , λ = − i \lambda=i , \lambda=-i λ = i , λ = − i λ = 0 \lambda=0 λ = 0
(ب) A A A 3 × 3 3 \times 3 3 × 3 λ = i , λ = − i \lambda=i , \lambda=-i λ = i , λ = − i λ = − 1 \lambda=-1 λ = − 1
حل: از این موضوع استفاده میکنیم که ضرب همه مقادیر ویژه ماتریس A A A A A A
(الف) دترمینان ماتریس A A A det ( A ) = i ⋅ ( − i ) ⋅ 0 = 0 \det(A) = i\cdot (-i)\cdot 0 = 0 det ( A ) = i ⋅ ( − i ) ⋅ 0 = 0 A A A
(ب) در این حالت، داریم: det ( A ) = i ⋅ ( − i ) ⋅ ( − 1 ) = − 1 \det(A) = i\cdot (-i)\cdot (-1)=-1 det ( A ) = i ⋅ ( − i ) ⋅ ( − 1 ) = − 1 A A A
برای پیدا کردن عبارت A − 1 A ^ { -1} A − 1 A A A
p ( λ ) = ( λ − i ) ( λ + i ) ( λ + 1 ) = λ 3 + λ 2 + λ + 1. \large p ( \lambda ) = ( \lambda - i ) ( \lambda + i ) ( \lambda + 1 ) = \lambda ^ 3 + \lambda ^ 2 + \lambda + 1 . p ( λ ) = ( λ − i ) ( λ + i ) ( λ + 1 ) = λ 3 + λ 2 + λ + 1.
طبق قضیه کیلی-همیلتون، ماتریس A A A
A 3 + A 2 + A + I = O \large A ^ 3 + A ^ 2 + A + I = O A 3 + A 2 + A + I = O
که در آن، O O O
I = − A – A 2 – A 3 = A ( − I – A – A 2 ) . \large I = - A – A ^ 2 – A ^ 3 = A ( - I – A – A ^ 2 ) . I = − A – A 2 – A 3 = A ( − I – A – A 2 ) .
اگر A − 1 A ^ { - 1} A − 1
A − 1 = − I – A – A 2 . \large A ^ { - 1 } = - I – A – A ^ 2 . A − 1 = − I – A – A 2 .
مثال ۷
فرض کنید A A A 2 × 2 2 \times 2 2 × 2 − 1 -1 − 1 3 3 3 n n n a n a _ n a n b n b _ n b n A n + 1 = a n A + b n I A^{n+1}=a_nA+b_nI A n + 1 = a n A + b n I I I I 2 × 2 2 \times 2 2 × 2
حل: از آنجایی که − 1 -1 − 1 3 3 3 A A A A A A
( t + 1 ) ( t − 3 ) = t 2 − 2 t − 3. \large ( t + 1 ) ( t - 3 ) = t^ 2 - 2 t - 3 . ( t + 1 ) ( t − 3 ) = t 2 − 2 t − 3.
طبق قضیه کیلی-همیلتون، داریم:
A 2 − 2 A − 3 I = O , \large A ^ 2 - 2 A - 3 I = O , A 2 − 2 A − 3 I = O ,
که در آن، O O O 2 × 2 2 \times 2 2 × 2
بنابراین، داریم:
A 2 = 2 A + 3 I , ( ∗ ) \large A ^ 2 = 2 A+ 3 I , \;\;\;\;\;\;\; (*) A 2 = 2 A + 3 I , ( ∗ )
و در نتیجه، a 1 = 2 , b 1 = 3 a_1=2, b_1=3 a 1 = 2 , b 1 = 3
با ضرب (*) در A A A
A 3 = A A 2 = 2 A 2 + 3 A = 2 ( 2 A + 3 I ) + 3 A = 7 A + 6 I . \large \begin {align*} A ^ 3 & = A A ^ 2 = 2 A^ 2 + 3 A \\ & = 2 ( 2 A + 3 I ) + 3 A \\ & = 7 A + 6 I . \end {align*} A 3 = A A 2 = 2 A 2 + 3 A = 2 ( 2 A + 3 I ) + 3 A = 7 A + 6 I .
بنابراین، a 2 = 7 , b 2 = 6 a_2=7, b_2=6 a 2 = 7 , b 2 = 6
در حالت کلی:
A n + 2 = A A n + 1 = A ( a n A + b n I ) = a n A 2 + b n A = a n ( 2 A + 3 I ) + b n A = ( 2 a n + b n ) A + ( 3 a n ) I . \large \begin {align*} A ^ { n + 2 } & = A A ^ { n + 1 } \\ & = A ( a _ n A + b _ n I ) \\ & = a _ nA ^ 2 +b _ n A \\ & = a _ n ( 2 A + 3 I ) + b _ n A \\ & = ( 2 a _ n + b _ n ) A + ( 3 a _ n ) I . \end {align*} A n + 2 = A A n + 1 = A ( a n A + b n I ) = a n A 2 + b n A = a n ( 2 A + 3 I ) + b n A = ( 2 a n + b n ) A + ( 3 a n ) I .
بنابراین، داریم:
a n + 1 = 2 a n + b n b n + 1 = 3 a n . \large \begin {align*} a _ { n + 1 } & =2 a _ n + b_ n \\ b _ { n + 1 } & = 3 a _ n . \end {align*} a n + 1 b n + 1 = 2 a n + b n = 3 a n .
دو معادله بالا، به رابطه بازگشتی زیر میانجامند:
a n + 2 = 2 a n + 1 + 3 a n \large a _ { n + 2 } = 2 a _ { n + 1 } + 3a _ { n } a n + 2 = 2 a n + 1 + 3 a n
که مقادیر اولیه آن، a 1 = 2 a _1 = 2 a 1 = 2 a 2 = 7 a _ 2 = 7 a 2 = 7
جمله عمومی a n a _ n a n ( a n ) n = 1 ∞ (a_n)_{n=1}^{\infty} ( a n ) n = 1 ∞
a n = 1 4 ( ( − 1 ) n + 3 n + 1 ) . \large a _ n = \frac { 1 } { 4 } \big ( ( - 1 ) ^ n + 3 ^ { n+ 1 } \big ) . a n = 4 1 ( ( − 1 ) n + 3 n + 1 ) .
همچنین، داریم:
b n = 3 a n − 1 = 3 4 ( ( − 1 ) n − 1 + 3 n ) . \large b _ n = 3 a _ { n - 1 } = \frac { 3 } { 4 } \big ( ( - 1 ) ^ { n - 1 } + 3 ^ { n } \big ) . b n = 3 a n − 1 = 4 3 ( ( − 1 ) n − 1 + 3 n ) .
این فرمول، برای n = 1 n =1 n = 1
در نهایت، A n A ^ n A n
A n = 1 4 ( ( − 1 ) n + 3 n + 1 ) A + 3 4 ( ( − 1 ) n − 1 + 3 n ) I \large \begin {align*} A ^ n = \frac { 1 } { 4 } \big ( ( - 1 ) ^ n + 3 ^ { n + 1 } \big ) A + \frac { 3 } { 4 } \big ( ( - 1 ) ^ { n - 1 } + 3 ^ { n } \big ) I \end {align*} A n = 4 1 ( ( − 1 ) n + 3 n + 1 ) A + 4 3 ( ( − 1 ) n − 1 + 3 n ) I
مثال 8
با استفاده از قضیه کیلی-همیلتون، معکوس ماتریس زیر را محاسبه کنید:
A = [ 7 2 − 2 − 6 − 1 2 6 2 − 1 ] \large A = \begin {bmatrix} 7 & 2 & - 2 \\ - 6 & - 1 & 2 \\ 6 & 2 & - 1 \end {bmatrix} A = 7 − 6 6 2 − 1 2 − 2 2 − 1
حل: برای استفاده از قضیه کیلی-همیلتون، ابتدا چندجملهای مشخصه p ( t ) p ( t) p ( t ) A A A I I I 3 × 3 3 \times 3 3 × 3
p ( t ) = det ( A − t I ) = ∣ 7 − t 2 − 2 − 6 − 1 − t 2 6 2 − 1 − t ∣ = ( 7 − t ) ∣ − 1 − t 2 2 − 1 − t ∣ − 2 ∣ − 6 2 6 − 1 − t ∣ + ( − 2 ) ∣ − 6 − 1 − t 6 2 ∣ = − t 3 + 5 t 2 − 7 t + 3. \large \begin {align*} p ( t ) & = \det ( A - t I ) = \begin {vmatrix} 7-t & 2 & -2 \\ -6 &-1-t &2 \\ 6 & 2 & -1-t \end {vmatrix} \\[6pt] & = ( 7 - t ) \begin {vmatrix} - 1 - t & 2 \\ 2 & - 1 - t \end {vmatrix} - 2 \begin {vmatrix} - 6 & 2 \\ 6 & - 1 - t \end {vmatrix} + ( - 2 ) \begin {vmatrix} - 6 & - 1 - t \\ 6 & 2 \end {vmatrix} \\[6pt] & \\ & = - t ^ 3 + 5 t ^ 2 - 7 t + 3 . \end {align*} p ( t ) = det ( A − t I ) = 7 − t − 6 6 2 − 1 − t 2 − 2 2 − 1 − t = ( 7 − t ) − 1 − t 2 2 − 1 − t − 2 − 6 6 2 − 1 − t + ( − 2 ) − 6 6 − 1 − t 2 = − t 3 + 5 t 2 − 7 t + 3.
بنابراین، چندجملهای مشخصه برابر است با:
p ( t ) = − t 3 + 5 t 2 − 7 t + 3 \large p ( t ) = - t ^ 3 + 5 t ^ 2 - 7 t + 3 p ( t ) = − t 3 + 5 t 2 − 7 t + 3
طبق قضیه کیلی-همیلتون، داریم:
O = p ( A ) = − A 3 + 5 A 2 − 7 A + 3 I , \large O = p ( A ) = - A ^ 3 + 5 A ^ 2 - 7 A + 3 I , O = p ( A ) = − A 3 + 5 A 2 − 7 A + 3 I ,
که در آن، O O O 3 × 3 3 \times 3 3 × 3
با کمی جابهجایی عبارات معادله مشخصه، میتوان نوشت:
A 3 − 5 A 2 + 7 A = 3 I ⇔ A ( A 2 − 5 A + 7 I ) = 3 I ⇔ A ( 1 3 ( A 2 − 5 A + 7 I ) ) = I . \large \begin {align*} & A ^ 3 - 5 A ^ 2 + 7 A = 3 I \\[6pt] & \Leftrightarrow A ( A ^ 2 - 5 A + 7 I ) = 3 I \\[6pt] & \Leftrightarrow A \left ( \frac { 1 } { 3 } ( A ^ 2 - 5 A + 7 I ) \right ) = I . \end {align*} A 3 − 5 A 2 + 7 A = 3 I ⇔ A ( A 2 − 5 A + 7 I ) = 3 I ⇔ A ( 3 1 ( A 2 − 5 A + 7 I ) ) = I .
و
( 1 3 ( A 2 − 5 A + 7 I ) ) A = I . \large \left ( \frac { 1 } { 3 } ( A ^ 2 - 5 A + 7 I ) \right ) A = I . ( 3 1 ( A 2 − 5 A + 7 I ) ) A = I .
با توجه به معادله اخیر، در مییابیم که معکوس ماتریس A A A
1 3 ( A 2 − 5 A + 7 I ) \large \frac { 1 } { 3 } ( A ^ 2 - 5 A + 7 I ) 3 1 ( A 2 − 5 A + 7 I )
بنابراین:
A − 1 = 1 3 ( A 2 − 5 A + 7 I ) = 1 3 ( [ 25 8 − 8 − 24 − 7 8 24 8 − 7 ] − 5 [ 7 2 − 2 − 6 − 1 2 6 2 − 1 ] + 7 [ 1 0 0 0 1 0 0 0 1 ] ) = 1 3 [ − 3 − 2 2 6 5 − 2 − 6 − 2 5 ] . \large \begin {align*} A ^ { - 1 } & = \frac { 1 } { 3 } ( A ^ 2 - 5 A + 7 I ) \\[6pt] & = \frac { 1 } { 3 } \left ( \, \begin {bmatrix} 25 & 8 & -8 \\ -24 &-7 &8 \\ 24 & 8 & -7 \end {bmatrix} - 5 \begin {bmatrix} 7 & 2 & -2 \\ -6 &-1 &2 \\ 6 & 2 & -1 \end {bmatrix} + 7 \begin {bmatrix} 1 & 0 & 0 \\ 0 &1 & 0 \\ 0 & 0 & 1 \end {bmatrix} \, \right ) \\[6pt] & = \frac { 1 } { 3 } \begin {bmatrix} -3 & -2 & 2 \\ 6 &5 &-2 \\ -6 & -2 & 5 \end {bmatrix}. \end{align*} A − 1 = 3 1 ( A 2 − 5 A + 7 I ) = 3 1 25 − 24 24 8 − 7 8 − 8 8 − 7 − 5 7 − 6 6 2 − 1 2 − 2 2 − 1 + 7 1 0 0 0 1 0 0 0 1 = 3 1 − 3 6 − 6 − 2 5 − 2 2 − 2 5 .
در نهایت، معکوس ماتریس A A A
A − 1 = 1 3 [ − 3 − 2 2 6 5 − 2 − 6 − 2 5 ] . \large A ^ { - 1 } = \frac { 1 } { 3 } \begin {bmatrix} - 3 & -2 & 2 \\ 6 & 5 &-2 \\ -6 & - 2 & 5 \end {bmatrix}. A − 1 = 3 1 − 3 6 − 6 − 2 5 − 2 2 − 2 5 .
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش قضیه کیلی همیلتون – از صفر تا صد (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی قضیه کیلیهمیلتون فیلم آموزشی قضیه کیلیهمیلتون برای ماتریس 2*2 فیلم آموزشی محاسبه معکوس ماتریس با قضیه کیلیهمیلتون فیلم آموزشی حل چند مثال از قضیه کیلیهمیلتون 
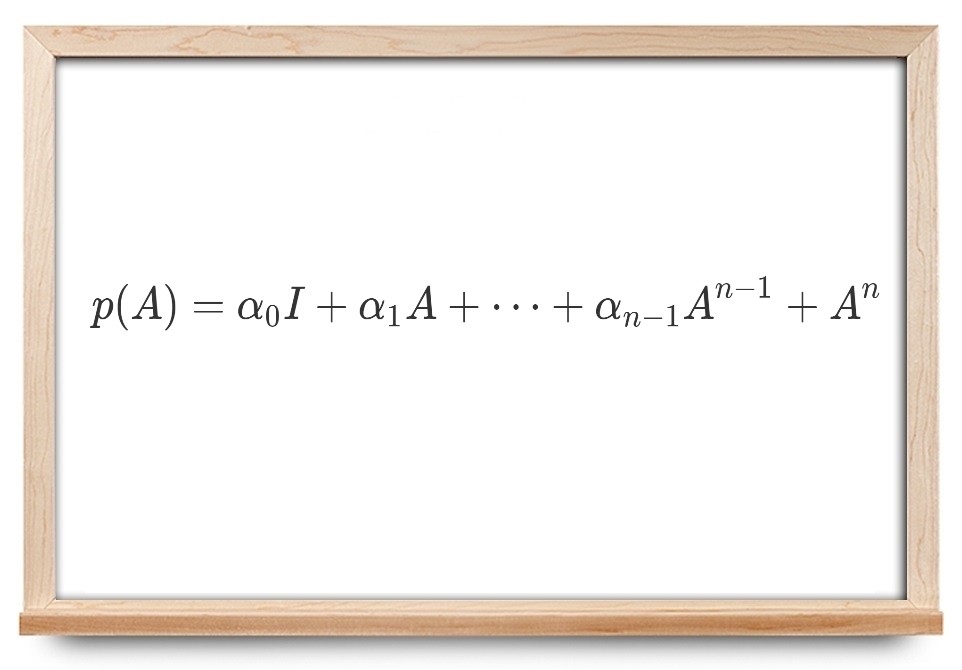













با سلام خیلی ممنون از آموزش بسیار خوبتون با زبانی ساده و مثالی خوب در زمان بسیار مناسبی این قضیه را توضیح دادین
سوالم مخالف هیچ موضع خاصی نبود که پاک کردید
پرسیدم با چی تدریس میکنن
قلم نوری؟
اسم و مشخصاتش همین؟
با تشکر از تدریس اقای سراح
یه سوال داشتم
شما با چه چزی می نویسید؟
قلم نوری؟ یا چیز دیگزی
اگر امکانش هست اسم و مدلش رو بگید
باتشکر