نیرو چیست؟ — تعریف، اثر، واحد و فرمول به زبان ساده

در زندگی روزمره بارها کلمه نیرو را شنیده‌ایم و از این کلمه بار‌ها در مبحث‌های مختلف استفاده کرده‌ایم. در علم فیزیک، به فشار یا کشش وارد شده بر هر جسمی به هنگام برهم‌کنش آن با جسم دیگر نیرو گفته می‌شود. در این مطلب در مورد نیرو صحبت می‌کنیم. ابتدا تلاش می‌کنیم به پرسش نیرو چیست پاسخ دهیم، سپس انواع نیرو را معرفی کرده و مثال‌های گوناگونی مرتبط با این کمیت را تحلیل و بررسی می‌کنیم.

نیرو چیست ؟

نیرو به هر تأثیری می‌گویند که باعث تغییر یک جسم شود. این تغییر می‌تواند در مورد حرکت، جهت یا ساختار هندسی آن باشد. به بیان دیگر در فیزیک، نیرو به هر تأثیری گفته می‌شود که باعث می‌شود یک جسم دچار تغییر خاصی شود، چه در مورد حرکت، جهت یا ساختار هندسی آن. کمیت نیرو به افتخار ایزاک نیوتن با واحد SI نیوتن اندازه گیری می‌شود.

نیرو کمیتی است که باعث می‌شود جسمی دارای جرم، سرعت خود را تغییر دهد، یعنی شتاب بگیرد، یا باعث تغییر شکل جسمِ انعطاف پذیر شود. نیرو را می‌توان با مفاهیم شهودی مانند فشار یا کشیدن نیز توصیف کرد. یک نیرو هم مقدار و هم جهت دارد و به همین دلیل آن را کمیت برداری می‌نامند.در این مبحث سعی داریم به پرسش نیرو چیست به زبان ساده پاسخ دهیم.

نکته: نیروها در نتیجه برهم‌کنش به وجود می‌آیند.

واحد نیرو چیست ؟

واحد نیرو نیوتن است و با نماد N نشان داده می‌شود.

یکای نیرو چیست ؟

همانطور که گفته شد، یکای نیرو نیوتن است که با نماد N آن را نشان می‌دهند.

فرمول نیرو چیست ؟

بر طبق قانون دوم نیوتن، فرمول نیرو، حاصل‌ضرب جرم جسم در شتاب حرکت آن یعنی F = ma است.

نکته: در قانون دوم نیوتن تعریف نیرو به صورت معادله زیر بیان می‌شود.

$$\sum \textbf{F} =m\textbf{a}$$

اثر نیرو چیست ؟

زمانی که نیرویی به جسمی وارد می‌شود سبب تغییر شکل و اندازه آن می‌شود. همچنین، اینرو می‌توان جسمی را به حرکت درآورد یا آن را متوقف کند. از جمله اثرات دیگر نیرو می‌توان به افزایش یا کاهش شتاب جسم نیز اشاره کرد. به بیان ساده، زمانی که برهم‌کنشی بین دو شئ وجود داشته باشد، این دو جسم بر یکدیگر نیرو وارد می‌کنند و این نیروها از نظر اندازه با یکدیگر برابر اما بر خلاف جهت یکدیگر هستند.

مهم ترین ویژگی نیرو چیست ؟

نیرو دارای ویژگی‌های مختلفی است که که از میان ‌آن‌ها می‌توان «به حرکت درآوردن جسم»، «توقف جسم متحرک»، «تغییر اندازه و جهت حرکت» و بسیاری ویژگی‌های دیگر را ذکر کرد که در این متن به آن‌ها اشاره شده است. در فهرست زیر، مهم‌ترین ویژگی‌های نیرو آورده شده است.

• به حرکت درآوردن جسم: اگر به توپی ضربه بزنید آن را به حرکت در می‌آورید. هنگامی که جسمی از ارتفاع رها می‌شود تحت نیروی جاذبه شروع به حرکت می‌کند. به هنگام وزش باد شاخه‌ها و بر‌گ‌های درختان حرکت می‌کنند.
• توقف جسم متحرک: توپی که بر روی زمین حرکت می‌کند پس از مدتی بر اثر نیروی اصطکاک متوقف خواهد شد. اتومبیل در حال حرکت پس از ترمز راننده متوقف می‌شود.
• تغییر اندازه حرکت: هنگامی که به جسم متحرکی در جهت حرکت آن نیرویی وارد شود، جسم با سرعت بزرگ‌تری حرکت خواهد کرد. وارد شدن نیرو در خلاف جهت حرکت جسم سبب کاهش اندازه سرعت می‌شود.
• تغییر جهت حرکت: هنگامی که توپی در مسیر حرکتش به دیواری برخورد می‌کند، جهت حرکت آن به دلیل وارد شدن نیرو از سمت دیوار تغییر خواهد کرد.
• تغییر شکل جسم: طول فنر به هنگام فشردن یا کشیده شدن تغییر می‌کند. شکل اسفنج با اعمال نیرو تغییر خواهد کرد.
• نیروی کلی صفر: هنگامی‌که دو نیروی وارد بر جسمی از نظر اندازه برابر و در خلاف جهت یکدیگر باشند، آنگاه نیروی کلی وارد بر جسم برابر صفر است.
• کمیت برداری: نیروی کمیتی برداری به شمار می‌آید. بنابراین، دارای اندازه و جهت است.
• تغییر بزرگی و اندازه نیرو: اگر اندازه و بزرگی نیرو یا هر دوی آن‌ها تغییر کنند، آنگاه اثر نیرو نیز تغییر خواهد کرد.

دسته بندی نیروها چیست ؟

نیروها به دو دسته نیروهای تماسی و غیرتماسی تقسیم می‌شوند.

نیروی تماسی چیست ؟

هنگامی که دو جسم در تماس فیزیکی با یکدیگر قرار داشته باشند، نیروی وارد شده بر آن‌ها از نوع نیروی تماسی خواهد بود. نیروی اصطکاک، نیروی کششی، نیروی عمود بر سطح، نیروی مقاومت هوا و نیروی ورودی یا محرک مثال‌هایی از نیروهای تماسی هستند.

نیروی غیر تماسی چیست ؟

به نیرویی که دو جسم دور از هم بر یکدیگر وارد می‌کنند نیروی غیرتماسی می‌گوییم. نیروی گرانشی، نیروی الکتریکی و نیروی مغناطیسی یکی از مهم‌ترین مثال‌های نیروهای غیرتماسی هستند.

نمایش ریاضی نیرو

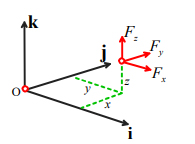
همان‌گونه که در توضیحات بالا اشاره شد نیرو یک بردار است، بنابراین علاوه بر اندازه، جهت نیز دارد. نمایش ریاضی نیرو همواره به صورت بردار خواهد بود. برای نوشتن نیرو به صورت بردار به نکات زیر توجه می‌کنیم.

1. بردارهای پایه {$${{\bf i}, \bf j, k}$$} یا {$${{\bf e_1}, \bf e_2, e_3}$$} به گونه‌ای انتخاب می‌شوند که دو به دو بر یکدیگر عمود باشند.
2. با استفاده از تجزیه بردارها در جهت بردارهای پایه، مولفه نیرو را در هر جهت به صورت $$(F_x,F_y,F_z)$$ یا $$(F_1,F_2,F_3)$$ به دست می‌‌آوریم.

در نتیجه نمایش برداری نیروی $$\bf F$$ به صورت زیر نوشته خواهد شد.

$$\textbf{F}=F_x\textbf{i}+F_y\textbf{j}+F_z\textbf{k}$$

حل نمونه سوال نیرو

در ادامه به منظور داشتن درک عمیق‌تر از مفهوم نیرو چیست به حل مثال‌های گوناگون می‌پردازیم. علاوه بر این، برای مطالعه بیشتر، قوانین نیوتون و نمودار جسم آزاد در انتهای همین مطلب بیان شده است.

مثال

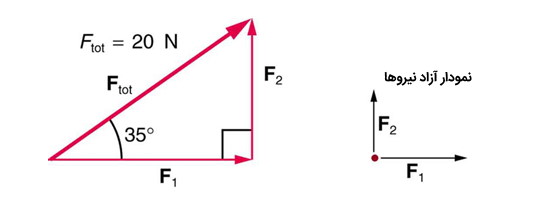
بزرگی نیروهای $$F_1$$ و $$F_2$$ را بیابید که برای بدست آوردن نیروی کل $$F_{tot}$$ نشان داده شده در شکل زیر با یکدیگر جمع شده‌اند.

پاسخ

برآیند دو نیروی $$F_1$$ و $$F_2$$ برابر با ۲۰ نیوتن است. بدین ترتیب می‌توان با توجه به زاویه داده شده بین نیروهای $$F_1$$ و برآیند آن‌ها و با استفاده از تجزیه برداری مقدار نیروی $$F_1$$ را به دست آورد. بدین ترتیب نیروی $$F_1$$ برابر است با:

$$\large F_1=F_{tot} \times \cos(35^{\circ})$$

در نتیجه نیروی $$F_1$$ برابر است با:

$$F_1=20 \times 0.819=16.38$$

برای به دست آوردن نیروی $$F_2$$ هم می‌توان از تجزیه برداری و هم می‌توان از قضیه فیثاغورس استفاده کرد. در این قسمت از قضیه فیثاغورس استفاده می‌کنیم. هر چند از شکل نیز می‌توانید درک کنید که نیروی $$F_2$$ برابر با نیروی برآیند در $$sin (35^{\circ})$$ است. اما به همین ترتیب از قضیه فیثاغورس نیز داریم:

$$\sqrt{F_1^2+F_2^2}=F_{tot}$$
$$\sqrt{(16.38)^2+F_2^2}=20$$
$$268.3044+F_2^2=400$$
$$F_2^2=\sqrt{400-268.3044}=131.67$$
$$F_2=11.47\ N$$

مثال

اگر وزن فردی بر روی زمین $$875 \ N$$ باشد، وزن او بر روی سیاره مشتری با شتاب سقوط آزاد $$25.9 \ \frac{m}{s^2}$$ چه قدر خواهد بود؟

پاسخ

وزن جسمی به جرم m بر روی زمین از رابطه W=mg محاسبه می‌شود. بنابراین، ابتدا جرم فرد را به دست می‌آوریم.

$$m=\frac{W}{g}=\frac{875 N}{9.80\ \frac{m}{s^2}}=89.3 \ kg$$

به منظور به دست آوردن وزن فرد بر روی سیاره مشتری، در رابطه بالا به جای g، $$a_{Jupiter}$$ را قرار می‌دهیم.

$$W_{Jupiter} = mg_{Jupiter} = (89.3 \ kg)(25.9\ \frac{m}{s^2}) = 2.31\times10^2\ N$$

مثال‌ کاربرد قوانین نیوتن

در ادامه یاد می‌گیریم کاربرد قانون‌های نیوتن در نیرو چیست و مثال‌هایی را حل می‌‌کنیم.

مثال

یک توپ به جرم $$1.12$$ کیلوگرم با شتاب $$1.11$$ متر بر مجذور ثانیه به سمت جلو حرکت می‌کند. نیروی خالص وارد بر توپ چه قدر است؟

پاسخ

طبق قانون دوم نیوتن نیرو برابر با جرم در شتاب است. بدین ترتیب با توجه به داده‌های مسئله داریم:

$$F=1.12 \times 1.11=1.24\ N$$

مثال

یک جعبه $$3.2$$ کیلوگرمی با نیرویی برابر با $$1.5$$ نیوتن کشیده می‌شود. شتاب حاصل از این حرکت چه قدر است؟

پاسخ

طبق قانون دوم نیوتن $$F=ma$$ است. با توجه به داده‌های مسئله داریم:

$$\begin{aligned} &\overrightarrow{F}=m\overrightarrow{a} \\ &1.5 N=3.2 k g(a) \\ &\frac{1.5 N}{3.2 k g}=a \\ &0.47 \frac{m}{s^{2}}=a \end{aligned}$$

مثال

جسمی به جرم ۲ کیلوگرم با سرعت ثابت به سمت بالا حرکت می‌کند. اگر شتاب گرانش $$9.8$$ متر بر مجذور ثانیه باشد، نیروی وارد بر جعبه چه قدر است؟

پاسخ

با توجه به اینکه حرکت با سرعت ثابت انجام می‌شود، شتاب حرکت صفر است. بدین ترتیب نیروی خالص بر جسم صفر است. نیروی خالص در این حرکت نیز مجموع دو نیروی گرانش و نیروی کشش به سمت بالا است.

$$F_{net}=F_{lift}+F_{gravity}$$

نیروی خالص برابر با صفر است و بدین ترتیب داریم:

$$\begin{aligned} &-F_{\text {gravity }}=F_{\text {lift }} \\ &-(m g)=F_{\text {lift }} \\ &-\left(-9.8 \frac{m}{s^{2}} * 2 k g\right)=F_{l i f t} \\ &-(-19.6 N)=F_{l i f t} \\ &19.6 N=F_{\text {lift }} \end{aligned}$$

مثال

سرعت یک جعبه ۱۲ کیلوگرمی از حالت سکون بعد از طی مسافت ۱۲ متر به ۳٫۴۵ متر بر ثانیه می‌رسد. نیروی وارد بر جعبه چه قدر است؟

پاسخ

با داشتن جرم و شتاب می‌توانیم نیروی وارد بر جسم را به دست آوریم. با استفاده از رابطه مستقل از زمان می‌توانیم شتاب حرکت را به دست آوریم. رابطه مستقل از زمان حرکت برابر است با:

$$\begin{aligned} &v_{f}^{2}=v_{i}^{2}+2 a \Delta x \\ &\left(3.45 \frac{m}{s}\right)^{2}=\left(0 \frac{m}{s}\right)^{2}+2 a(12 m) \end{aligned}$$

بدین ترتیب شتاب حرکت برابر است با:

$$a=0.496\ \frac{m}{s^2}$$

با به دست آوردن شتاب حرکت، نیروی وارد بر جسم برابر است با:

$$\begin{aligned} &F=m a \\ &F=12 k g * 0.496 \frac{m}{s^{2}} \\ &F=5.95 N \end{aligned}$$

مثال

جسمی به جرم 3/0 کیلوگرم با شتاب $$\textbf{a}=(2.0\textbf{i}+5.0\textbf{j}) \ \frac{m}{s^2}$$ حرکت می‌کند. بزرگی و جهت نیروی وارد شده بر این جسم را به دست آورید.

پاسخ

با توجه به قانون دوم نیوتن داریم.

$$\sum \textbf{F}=m \textbf{a}$$

در نتیجه نیروی وارد شده بر جسم به صورت زیر به دست خواهد آمد.

$$\textbf{F}=m \textbf{a} \\ = (3.0 \ kg)(2.0\textbf{i} \ + 5.0\textbf{j})\frac{m}{s^2}\\ =(6.0\textbf{i} \ + 15\textbf{j})$$

بزرگی نیرو نیز به صورت زیر محاسبه می‌شود.

$$F=\sqrt{(6.0N)^2\ + \ (15N)^2}=16N$$

مثال

دو نیرو هم‌زمان به ذره‌ای به جرم 3/2 کیلوگرم وارد می‌شوند اگر ذره با سرعت $$(3\ \frac{m}{s})\textbf{i} \ - \ (4\frac{m}{s})\textbf{j}$$ حرکت کند و یکی از نیروهای وارد شده بر ذره به صورت $$\textbf{F}_1 = (2N)\textbf{i} \ + \ (-6N) \textbf{j}$$ باشد، مقدار نیروی دوم چه قدر است؟

پاسخ

بر طبق قانون دوم نیوتن داریم.

$$\sum \textbf{F}=m \textbf{a}\\ \textbf{F}_1\ +\ \textbf{F}_2 = m\textbf{a}$$

از آنجایی که ذره با سرعت ثابت حرکت می‌کند، در نتیجه شتاب حرکت آن برابر با صفر خواهد بود. بنابراین داریم.

$$\textbf{F}_1\ +\ \textbf{F}_2 = m\textbf{a} \\ \textbf{F}_1\ +\ \textbf{F}_2 = 0 \\ \Rightarrow \textbf{F}_2\ = -\ \textbf{F}_1$$

در نتیجه نیروی دوم برابر با $$\textbf{F}_2\ = -\ \textbf{F}_1 = (-2N)\textbf{i} \ +\ (6N)\textbf{j}$$ است.

مثال

جسمی به جرم $$4.0 \ kg$$ در یک لحظه با سرعت $$3.0 \textbf{i} \ \frac{m}{s}$$ حرکت می‌کند. هشت ثانیه بعد سرعت جسم برابر $$(8.0 \textbf{i} \ +10.0\textbf{j})\ \frac{m}{s}$$ می‌شود. با فرض آن‌که نیروی ثابتی بر این جسم وارد خواهد شد، مولفه‌های نیرو و بزرگی آن را به دست آورید.

پاسخ

طبق صورت سوال نیروی وارد بر جسم ثابت است. در نتیجه،‌ شتاب حرکت جسم نیز ثابت خواهد بود و مقدار آن با استفاده از معادله‌های حرکت با شتاب ثابت به دست می‌آید. با توجه به مقادیر اولیه و نهایی سرعت داریم.

$$a_x=\frac{\triangle v_x}{\triangle t}= \frac{[(8.0 \frac{m}{s})-(3.0)\frac{m}{s})}{(8.0s)}=0.63 \ \frac{m}{s^2}$$

و

$$a_y=\frac{\triangle v_y}{\triangle t}= \frac{[(10.0 \frac{m}{s})-(0.0)\frac{m}{s})}{(8.0s)}=1.3 \ \frac{m}{s^2}$$

با استفاده از قانون دوم نیوتن، مولفه‌های نیرو را در هر راستا به دست می‌آوریم.

$$F_x=ma_x=(4.0kg)(0.63\frac{m}{s^2})=2.5 N \\ F_y=ma_y=(4.0kg)(1.3\frac{m}{s^2})=5.0 N$$

بزرگی نیرو نیز به صورت زیر محاسبه می‌شود.

$$F=\sqrt{(F_x^2 \ + F_y^2)} = \sqrt{(2.5N)^2 \ + \ (5.0N)^2}\ = 5.6 \ N$$

مثال

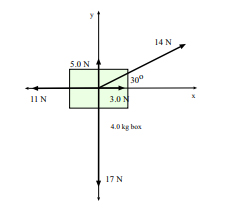
بر جعبه‌ای به جرم $$4.0\ kg$$، پنج نیرو مطابق تصویر نشان داده شده وارد می‌شوند. اندازه و بزرگی شتاب حرکت جعبه را به دست آورید.

پاسخ

در ابتدا اندازه نیروهای وارد شده بر جعبه را در دو راستای x و y به دست می‌آوریم.

$$\sum F_x = -11N\ + \ 14Ncos30^o\ + \ 3.0N = 4.1\ N$$

و

$$\sum F_y = +5.0N\ + \ 14Nsin30^o\ - \ 17N = -5.0\ N$$

با توجه به مقادیر به دست آمده برای مولفه‌های نیرو در دو راستای‌ x و y، نیروی کل وارد بر جعبه برابر خواهد بود با:

$$\sum F = (4.1\ N)\textbf{i}\ + (-5.0 \ N)\textbf{j}$$

با استفاده از رابطه $$\textbf{a} = \frac{\sum\textbf{F}}{m}$$ مولفه‌های شتاب در راستای x و y به صورت زیر به دست خواهند آمد.

$$a_x=\frac{\sum F_x}{m}=\frac{(4.1 \ N)}{(4.0\ kg)}= 1.0 \ \frac{m}{s^2}\\ a_y=\frac{\sum F_y}{m}=\frac{(-5.0 \ N)}{(4.0\ kg)}= -1.2 \ \frac{m}{s^2}$$

در نتیجه، نمایش برداری شتاب به صورت $$\textbf{a}= (1.0\ \frac{m}{s^2})\textbf{i} \ + \ (-1.2\ \frac{m}{s^2})\textbf{j}$$ نوشته می‌شود. برای به دست آوردن بزرگی شتاب حرکت جعبه داریم:

$$a=\sqrt{a_x^2+a_y^2}\ = \sqrt{(1.0\frac{m}{s^2})^2\ + (-1.2\frac{m}{s^2})^2}=1.6 \ \frac{m}{s^2}$$

به منظور به دست آوردن جهت بردار داریم:

$$tan\theta=\frac{a_y}{a_x}=\frac{-1.2}{1.0}=-1.2 \\ \theta = tan^{-1}(-1.2)=-50^o$$

مثال

موشکی با جرم $$5 \times 10^5$$ کیلوگرم مستقیماً به سمت بالا شتاب می‌گیرد. موتورهای این موشک دارای نیروی رانش $$1.250 \times 10^7$$ هستند و نیروی مقاومت هوا $$4.50 \times 10^6$$ نیوتن است. شتاب موشک چقدر است؟

پاسخ

با استفاده از نمودار نیروهای آزاد وارد بر جسم به شکل زیر:

$$F_{\text {net }}=T-f-m g=\mathrm{ma}$$

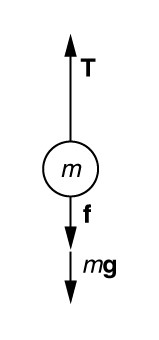
بدین ترتیب شتاب جسم برابر است با:

$$a=\frac{T-f-\mathrm{mg}}{m}=\\ \frac{1.250 \times 10^{7} \mathrm{~N}-4.50 \times 10^{6} N-\left(5.00 \times 10^{5} \mathrm{~kg}\right)\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)}{5.00 \times 10^{5} \mathrm{~kg}}=\\ 6.20 \mathrm{~m} / \mathrm{s}^{2}$$

مثال قانون دوم نیوتن

در تصویر نشان داده شده در زیر کشش هر طناب را به دست آورید‌ (از جرم طناب‌ها چشم‌پوشی کنید).

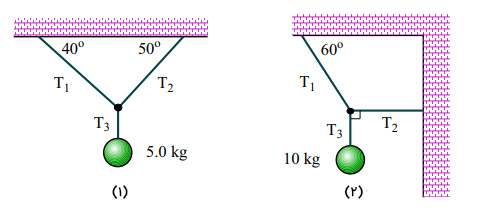
پاسخ

قسمت (۱). در قسمت ۱ جسم به جرم 5/0 کیلوگرم را با $$m_1$$ نشان می‌دهیم. نیروهای وارد بر $$m_1$$ نیروی وزن به سمت پایین و نیروی کشش طناب ($$T_3$$) به سمت بالا خواهند بود. از آنجایی که این جسم در حال سکون قرار دارد برآیند نیروهای وارد شده بر آن برابر صفر است. در نتیجه داریم.

$$T_3= m_1g= (5.0\ kg)(9.80 \ \frac{m}{s^2}) = 49 \ N$$

اکنون به نیروهای اعمالی بر نقطه اتصال سه طناب نگاه می‌کنیم (تصویر نشان داده شده در ادامه).

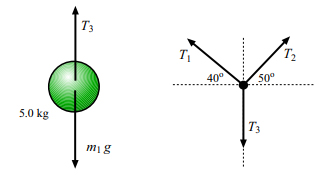
از آنجایی که نقطه اتصال ساکن است جمع نیروهای اعمال شده بر آن صفر خواهد بود. در واقع جمع نیروهای عمودی و افقی به طور جداگانه برابر صفر می‌شوند. برآیند نیروهای افقی برابر است با.

$$-T_1cos\ 40^o\ + T_2cos \ 50^o\ = 0$$

با استفاده از رابطه بالا مقدار کشش در طناب ۲ را بر حسب کشش طناب ۱ به دست می‌آوریم.

$$T_2cos \ 50^o\ = T_1cos\ 40^o\ \Rightarrow T_2 = \frac{cos\ 40^o}{cos \ 50^o }\ T_2 = 1.19 \ T_1$$

جمع نیروهای عمودی نیز برابر صفر خواهد بود بنابراین داریم.

$$T_1sin \ 40^o\ + T_2sin\ 50^o\ -T_3 = 0$$

مقدار $$T_3$$ را به دست آوردیم. با جایگزینی رابطه به دست آمده برای $$T_2$$ خواهیم داشت.

$$T_1sin \ 40^o\ + (1.19\ T_1)sin\ 50^o\ -49 \ N = 0$$

اکنون می‌توانیم مقدار $$T_1$$ را به دست آوریم.

$$(1.56) T_1 = 49 \ N \\ T_1 = \frac{49 \ N}{(1.56) } = 31.5 \ N$$

با به دست آوردن مقدار $$T_1$$، مقدار $$T_2$$ به صورت زیر به دست خواهد آمد.

$$T_2 = (1.19) T_1 = (1.19)(31.5 \ N) =37.5 \ N$$

قسمت (۲). اکنون سیستم (۲) را مطالعه می‌کنیم. مانند قسمت (۱)‌ نیروی کل وارد شده بر جرم $$‌m_2$$ صفر است. بنابراین داریم.

$$T_3= m_2g= (10\ kg)(9.80 \ \frac{m}{s^2}) = 98 \ N$$

مانند قسمت (۱)‌ نقطه اتصال طناب‌ها را در نظر می‌گیریم. برای مولفه افقی نیروهای وارد شده بر این نقطه داریم.

$$-T_1cos \ 60^o \ + T_2=0\Rightarrow T_2=T_1cos \ 60^o$$

برای مولفه عمودی نیروهای وارد شده خواهیم داشت.

$$T_1sin \ 60^o \ - T_3=0$$

با دانستن مقدار $$T_3$$، مقدار $$T_1$$ را به دست می‌آوریم.

$$T_1 = \frac{T_3}{sin \ 60^o}= \frac{98 \ N}{sin \ 60^o}=113 \ N$$

اکنون با به دست آوردن مقدار $$T_1$$، می‌توانیم کشش طناب ۲ را نیز به دست آوریم.

$$T_2 = T_1 cos \ 60^o = (113 \ N) cos \ 60^o = 56.6 \ N$$

مثال اول سطح شیبدار

در شکل زیر اگر زاویه سطح شیبدار ۴۱ درجه و جرم جسم ۱۴٫۲ کیلوگرم باشد، نیروی عمود بر سطح چه قدر است؟

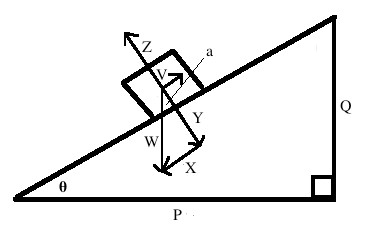
پاسخ

همان طور که می‌دانید نیروی عمود بر سطح یا نیروی نرمال، عمود بر سطحی است که جسم روی آن قرار می‌گیرد. بدین ترتیب راستای عمود بر سطح شیبدار را محور y و در راستای سطح شیبدار را محور x در نظر می‌گیریم. بدین ترتیب نیروی عمود بر سطح برابر با مولفه عمودی وزن می‌شود و داریم:

$$N=mg\ \cos(\theta)=14.2 \times 9.8 \times \cos(41^{\circ})$$

$$N=105.03\ N$$

مثال دوم سطح شیب دار

جعبه‌ای به جرم $$m=2.0 \ kg$$ بر روی سطح شیب‌داری با زاویه $$\theta = 60^o$$ توسط نیروی افقی F در حالت سکون قرار گرفته است. مقادیر زیر را به دست آورید.

(۱)‌ نیروی افقی ‌F.

(۲)‌ نیروی عمودی وارد شده بر جعبه از طرف سطح شیب‌دار (از اصطکاک چشم‌پوشی کنید).

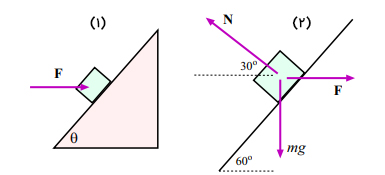
پاسخ

(۱): در ابتدا نمودار جسم آزاد را برای جعبه رسم می‌کنیم (تصویر ۲). از آنجایی که جعبه در حال تعادل است در نتیجه برآیند نیروهای وارد شده بر آن برابر صفر خواهد بود. برآیند نیروها در راستای عمود به صورت زیر نوشته می‌شود.

$$N \ sin\ 30^o-mg = 0 \Rightarrow N=\frac{mg}{sin \ 30^o}$$

با جایگزینی داده‌های مساله، مقدار N به صورت زیر به دست خواهد آمد.

$$N=\frac{(2.0 \ kg) ( 9.80 \frac{m}{s^2})}{sin \ 30^o}= 39.2 \ N$$

همچنین برآیند نیروهای افقی نیز برابر با صفر است.

$$F-Ncos\ 30^o = 0\Rightarrow F= Ncos\ 30^o = (39.2\ N)cos\ 30^o = 33.9 \ N$$

در نتیجه مقدار نیروی اعمالی بر جعبه برابر 33/9 نیوتن به دست می‌آید.

(۲)‌: مقدار نیروی عمودی در قسمت (۱) برابر 39.2 نیوتن به دست آمد.

مثال کشش طناب

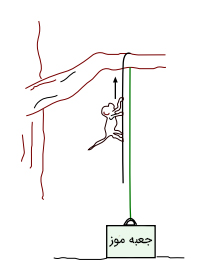
میمونی به جرم 10 کیلوگرم همان‌گونه که در تصویر زیر نشان داده شده است از طناب بدون وزنی بالا می‌رود. سپس جعبه‌ای به جرم 15 کیلوگرم را می‌بیند و برای رسیدن به آن از طناب پایین می‌رود. (۱) حداقل شتابی که میمون باید داشته باشد تا بتواند جعبه را از زمین بلند کند چه مقدار است؟ اگر پس از بلند شدن جعبه از روی زمین، میمون از طناب بالا نرود مقدارهای (۲) شتاب میمون و (۳)‌کشش طناب را به دست آورید (از اصطکاک بین طناب و شاخه درخت چشم‌پوشی کنید).

پاسخ

(۱): قبل از حل پرسش، نیروهای وارد شده بر میمون و جعبه موز را تعیین می‌کنیم. نمودار جسم آزادِ میمون و جعبه موز در تصویر زیر نشان داده شده است.

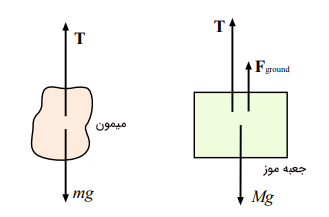
میمون از طناب بالا می‌رود، بنابراین نیروی رو به بالایی به اندازه T (کشش طناب)‌ وارد می‌کند. نیروی جاذبه mg به سمت پایین بر میمون وارد می‌شود. نیروهای وارد شده بر جعبه موز، نیروی جاذبه زمین به سمت پایین (Mg)، نیروی کشش طناب به سمت بالا (T) و نیروی عمودی از طرف زمین بر جعبه ($$F_{ground}$$) هستند.

در قسمت (۱) پرسش، میمون از طناب بالا می‌رود. فرض کنید شتاب میمون و جعبه موز به ترتیب با $$a_{y,monkey}$$ و $$a_{y,box}$$ نشان داده می‌شوند. برای شتاب میمون مطابق با قانون دوم نیوتن داریم.

$$T-mg=ma_{y,monkey} \\ (1)$$

هنگامی که جعبه بر روی زمین قرار دارد شتاب آن برابر صفر خواهد بود. در نتیجه برآیند نیروهای وارد بر آن صفر خواهند شد.

$$T+F_{ground}=Mg$$

به هنگام بلند شدن جعبه از زمین خواهیم داشت.

$$T-Mg=Ma_{box}$$

در قسمت (۱) پرسش حداقل شتابی که میمون باید داشته باشد تا بتواند جعبه را از زمین بلند کند به دست آوریم. حداقل شتاب زمانی به دست می‌آید که جعبه موز در آستانه بلند شده از زمین قرار بگیرد، در این‌ صورت نیروی $$F_{ground}$$ برابر صفر خواهد شد.

$$T-Mg =0 \ \Rightarrow T=Mg$$

با جایگزینی مقدار به دست آمده برای ‌T در رابطه (۱) داریم.

$$Mg-mg=ma_{y,monkey} \ \Rightarrow a_{monkey} = \frac{(M-m)g}{m}$$

با جایگزینی مقدارهای داده شده در رابطه بالا خواهیم داشت.

$$a_{monkey}=\frac{(15\ kg\ - 10\ kg)(9.80 \ \frac{m}{s^2})}{10 \ kg}=4.9\ \frac{m}{s^2}$$

اگر میمون با شتاب $$4.9\ \frac{m}{s^2}$$ از طناب بالا برود، جعبه موز در آستانه بلند شدن از زمین قرار خواهد گرفت.

(۲): اگر پس از بلند شدن جعبه از زمین، میمون متوقف شود مسافتی که جعبه به سمت پایین حرکت می‌کند با مسافت طی شده توسط میمون به سمت بالا برابر خواهد بود. با گرفتن جهت مثبت به سمت بالا خواهیم داشت.

$$a_{monkey}=-a_{box}=a$$

برای حرکت میمون طبق قانون دوم نیوتن داریم.

$$T-mg=ma \\ (1)$$

برای جعبه موز نیز خواهیم داشت.

$$T-Mg=M(-a) \\ (2)$$

با استفاده از رابطه (۱) کشش نخ را به دست می‌آوریم.

$$T=mg+ma$$

با جایگزینی رابطه به دست آمده برای کشش نخ در معادله (۲) داریم.

$$mg+ma-Mg=Ma \ \Rightarrow \ ma+Ma=Mg-mg$$

در نتیجه شتاب حرکت به صورت زیر به دست خواهد آمد.

$$(M+m) a=(M-m) g \ \Rightarrow \ a= \frac{(M-m)}{(M+m)}\ g$$

با جایگذاری داده‌های پرسش در رابطه بالا شتاب به صورت زیر دست خواهد آمد.

$$a= \frac{(15.0 \ kg - 10.0 \ kg)}{(15.0 \ kg + 10.0 \ kg)} \ (9.80 \frac{m}{s^2}) = 2.0 \frac{m}{s^2}$$

هنگامی که میمون طناب را محکم گرفته است هر دو جرم آزادانه حرکت خواهند کرد. در نتیجه، شتاب میمون نیز برابر $$2.0 \frac{m}{s^2}$$ و سمت بالا است.

(۳) با داشتن مقدار شتاب، به راحتی می‌توانیم اندازه کشش طناب را به دست آوریم. با استفاده از رابطه (۱) داریم.

$$T=mg+ma=m(g+a)= (10.0 \ kg) (9.80 \ \frac{m}{s^2}+2.0 \ \frac{m}{s^2})= 118 \ N$$

بنابراین کششش طناب برابر 118 نیوتن است.

مثال اول قرقره

جرم M توسط نیروی F و سیستم قرقره نمایش داده شده در تصویر زیر نگه داشته شده است. قرقره‌ها را بدون جرم و اصطکاک در نظر بگیرید. مطلوب است (۱)‌ کشش‌ در طناب‌های ۱ تا ۵ و (۲) بزرگی نیروی F.

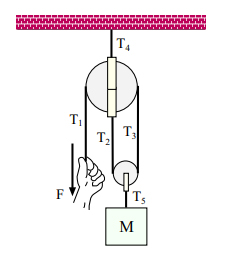
پاسخ

(۱): ذکر این نکته مهم است که جرم M و قرقره‌ها بی‌حرکت هستند. بنابراین، نیروی کل وارد شده بر هر جرمی برابر صفر خواهد بود.

هنگامی که طناب بدون جرمی از قرقره بدون جرم و اصطکاکی می‌گذرد کشش طناب در دو سمت قرقره یکسان خواهد بود. همان‌گونه که در شکل نشان داده شده است از قرقره بزرگ‌تر و کوچک‌تر طناب یکسانی عبور کرده است بنابراین کشش‌های $$T_1, \ T_2$$ و $$T_3$$ با یکدیگر برابر خواهند بود:

$$T_1=T_2=T_3$$

اکنون نیروهای وارد شده بر جرم M را در نظر می‌گیریم. نیروی گرانش Mg‌ به سمت پایین و نیروی کشش $$T_5$$ به سمت بالا بر این جرم وارد می‌شوند. از آنجایی که جرم‌ M در حالت تعادل قرار دارد در نتیجه داریم:

$$T_5=Mg$$

اکنون نیروهای وارد شده بر قرقره کوچک‌تر را در نظر می‌گیریم. همان‌طور که در تصویر مشاهده می‌کنید بر این قرقره نیروی کشش $$T_5$$ به سمت پایین و دو نیروی $$T_2$$ و $$T_3$$ به سمت بالا وارد می‌شوند.

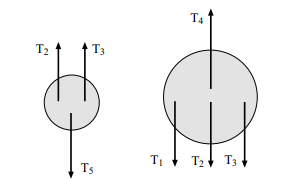
از آنجایی که قرقره ساکن است جمع برداری این نیروها صفر خواهد بود.

$$T_2+T_3-T_5=0$$

می‌دانیم $$T_5=Mg$$، در نتیجه خواهیم داشت:

$$2T_2-Mg=0$$

بنابراین داریم:

$$T_2=\frac{Mg}{2} \ \Rightarrow \ T_3=T_2 = \frac{Mg}{2}$$

همچنین

$$T_1=T_2 = \frac{Mg}{2}$$

اکنون نیروهای وارد شده بر قرقره بزرگ‌تر را در نظر بگیرید. کشش $$T_4$$ از طرف طنابی که به سقف وصل شده است به سمت بالا بر آن وارد می‌شود. همچنین کشش‌های $$T_1, \ T_2$$ و $$T_3$$ نیز به سمت پایین بر این قرقره وارد خواهند شد. جمع برداری این نیروها باید صفر شود در نتیجه داریم:

$$T_4-T_1-T_2-T_3=0$$

در رابطه بالا، کشش $$T_4$$ تنها مقدار مجهول است.

$$T_4=T_1+T_2+T_3=\frac{Mg}{2}+\frac{Mg}{2}+\frac{Mg}{2}=\frac{3Mg}{2}$$

(۲): نیروی F نیرویی است که از طرف دست فرد و به سمت پایین بر طناب وارد می‌شود. این نیرو با نیروی کشش طناب بر روی دست، یعنی $$T_1$$ برابر خواهد بود.

$$F=T_1=\frac{Mg}{2}$$

مثال دوم قرقره

جرم $$m_1$$ بر روی میز بدون اصطکاکی قرار دارد و از طریق قرقره بدون جرم $$P_1$$ به قرقره بدون جرم و ثابت $$P_2$$ به جرم $$m_2$$ وصل شده است. (۱) اگر $$a_1$$ و $$a_2$$ به ترتیب شتاب‌ جرم‌های $$m_1$$ و $$m_2$$ باشند، چه رابطه‌ای بین این دو شتاب برقرار است. (۲) نیروهای کشش نخ چقدر است؟ (۳)‌ شتاب‌های $$a_1$$ و $$a_2$$ را بر حسب $$m_1$$ و $$m_2$$ به دست آورید.

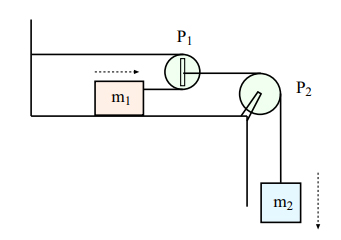
پاسخ

مطابق تصویر نشان داده شده، اگر جرم $$m_2$$ به سمت پایین حرکت کند، جرم $$m_1$$ به سمت راست حرکت خواهد کرد. سوالی که مطرح می‌شود آن است که اندازه‌های مسافت جابجا شده، سرعت‌ و شتاب دو جرم $$m_1$$ و $$m_2$$ چگونه با یکدیگر مقایسه می‌شوند؟

بهترین راه برای نشان دادن رابطه بین $$a_1$$ و $$a_2$$ در ادامه توضیح داده می‌شود. جرم $$m_1$$ و قرقره $$P_1$$ در تصویر زیر نشان داده شده‌اند.

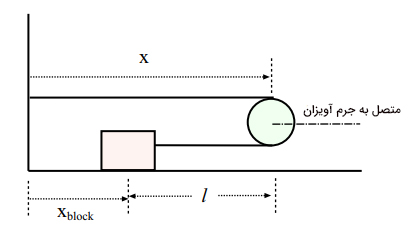
فاصله بین دیوار و قرقره متحرک $$P_1$$ برابر ‌x است. مکان جرم $$m_2$$ نیز با x اندازه گرفته می‌شود. طول طناب بین جرم $$m_1$$ و قرقره $$P_1$$ برابر $$l$$ خواهد بود. در نتیجه فاصله بین جرم $$m_1$$ و دیوار برابر خواهد بود با:

$$x_{block}=x-l$$

ذکر این نکته مهم است که بخشی از طول طناب که به دور قرقره پیچیده شده در محاسبات لخاظ نشده است (از آن چشم‌پوشی کرده‌ایم). طول کل طناب برابر با $$L=x+l$$ خواهد بود که با زمان تغییر نمی‌کند. با توجه به آن‌که $$l=L-x$$ داریم:

$$x_{block}=x-(L-x)=2x-L$$

با توجه به این نکته که مقدار L ثابت است، از دو طرف رابطه بالا دو بار مشتق می‌گیریم.

$$\frac{\text{d}^2x_{block}}{\text{d}t^2}=2\frac{\text{d}^2x}{\text{d}t^2}$$

طرف چپ معادله بالا شتاب جرم $$m_1$$ و طرف راست آن شتاب جرم $$m_2$$ است. در نتیجه، شتاب جرم $$m_1$$ دو برابر شتاب جرم $$m_2$$ خواهد بود.

$$a=2a_2 \\ (1)$$

در واقع، هنگامی که جسم ۲ به اندازه x به سمت پایین حرکت می‌کند طناب و در نتیجه جسم ۱ به اندازه 2x جابجا خواهند شد.

(۲) تصویر زیر نمودار جسم آزاد جسم‌های ۱، ۲ و قرقره $$P_1$$ را نشان می‌دهد.

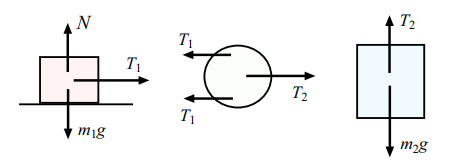
نیروهای وارد بر جرم $$m_1$$ عبارتند از:

1. نیروی وزن $$m_1g$$ به سمت پایین.
2. نیروی عمودی سطح (N) به سمت بالا.
3. نیروی کشش نخ ($$T_1$$) به سمت راست.

از آنجایی که جرم $$m_1$$ در راستای عمود بر سطح حرکتی ندارد، در نتیجه برآیند نیروهای وارد بر آن در راستای عمودی برابر صفر خواهد بود.

$$T_1=m_1a_1 \\ (2)$$

نیروهای وارد بر قرقره $$P_1$$ عبارتند از :

1. نیروی $$T_1$$ که بر بالا و پایین قرقره و به سمت چپ بر آن وارد می‌شوند.
2. نیروی $$T_2$$ که قرقره را به سمت راست می‌کشد.

از آنجایی که قرقره $$P_1$$ بدون جرم در نظر گرفته شده است، جمع برداری نیروهای وارد بر آن برابر صفر خواهند شد.

$$T_2-2T_1=0 \\ (3)$$

در پایان جرم $$m_۲$$ را در نظر می‌گیریم. این جرم با شتاب $$a_2$$ به سمت پایین حرکت خواهد کرد. در نتیجه بر طبق قانون دوم نیوتن داریم.

$$m_2g-T_2=m_2a_2 \\ (4)$$

مقدارهای $$T_1, \ T_2, \ a_1$$ و $$a_2$$ باید محاسبه شوند.

با جایگزین کردن رابطه (۱)‌ در رابطه (۲) داریم:

$$T_1=2m_1a_2$$

با قرار دادن رابطه به دست آمده در بالا در رابطه (۳)‌ خواهیم داشت:

$$T_2-2T_1=T_2-4m_1a_2 \ \Rightarrow \ T_2=4m_1a_2$$

با قرار دادن مقدار به دست آمدن برای $$T_2$$ در رابطه (۴) داریم:

$$m_2g-4m_1a_2=m_2a_2$$

 با حل معادله بالا بر حسب $$a_2$$ خواهیم داشت:

$$m_2g=a_2(4m_1\ + \ m_2) \ \Rightarrow \ a_2= \frac{m_2g}{(4m_1\ + \ m_2)}$$

شتاب $$a_1$$ نیز از رابطه زیر به دست می‌آید.

$$a_1= 2a_2= \frac{2m_2g}{(4m_1\ + \ m_2)}$$

با استفاده از روابط بالا کشش‌های $$T_1$$ و $$T_2$$ نیز به صورت زیر به دست خواهند آمد.

$$T_1=m_1a_1= \frac{2m_1m_2g}{(4m_1\ + \ m_2)} \\ T_2=m_2a_2= \frac{4m_1m_2g}{(4m_1\ + \ m_2)}$$

عامل ایجاد نیرو چیست ؟

عامل‌‌های زیادی مانند جاذبه، الکترواستاتیک و الکترومغناطیس سبب ایجاد نیرو می‌شوند. برخی از نیروهای گفته شده با استفاده از قانون‌های جهانی توصیف می‌شوند. انواع نیروها و علامت اختصاری آن‌ها در ادامه این متن آورده شده‌اند.

نیروی محرک یا ورودی $$F_{app}$$

نیروی ورودی یا محرک، نیرویی است که توسط شخص یا جسم دیگری به جسم وارد می‌شود. اگر شخصی در حال هل دادن میز در سراسر یک اتاق باشد، نیرویی بر جسم وارد می‌شود. نیروی محرک به صورت عمومی به عنوان نیرویی شناخته می‌شود که یک فرد به یک جسم اعمال می‌کند.

نیروی گرانش یا وزن $$F_{grav}$$

نیروی گرانش نیرویی است که با آن زمین، ماه، یا سایر اجسام بسیار بزرگ جسم دیگری را به سمت خود جذب می‌کنند. طبق تعریف، این کمیت برابر با وزن جسم است. تمام اجسام روی زمین نیروی گرانشی را تجربه می‌کنند که آن‌ها را به سمت مرکز زمین و به سمت پایین می‌کشد. نیروی گرانش روی زمین همیشه برابر با وزن جسم است که با معادله زیر بدست می‌آید:

$$F_{grav}=m.g$$

که $$g=9.8$$ نیوتن بر کیلوگرم (روی زمین) و m = جرم (بر حسب کیلوگرم) است.

نیروی عمود بر سطح $$F_{norm}$$

نیروی نرمال یا عمود بر سطح، نیروی پشتیبانی است که بر جسمی وارد می‌شود که با جسم ثابت دیگری در تماس است. به عنوان مثال، اگر کتابی بر روی سطحی قرار گرفته باشد، سطح آن به منظور تحمل وزن کتاب، نیرویی رو به بالا بر کتاب وارد می‌کند. در مواردی، یک نیروی عمود بر سطح به صورت افقی بین دو جسمی که با یکدیگر در تماس هستند وارد می شود. به عنوان مثال، اگر فردی به دیوار تکیه دهد، دیوار به صورت افقی به فرد فشار می آورد.

نیروی اصطکاک $$F_{frict}$$

نیروی اصطکاک نیرویی است که توسط یک سطح به هنگام حرکت جسم بر روی آن یا جسمی که در تلاش است تا بر روی جسم دیگر حرکت کند وارد می‌شود. حداقل دو نوع نیروی اصطکاک وجود دارد که عبارت از اصطکاک جنبشی و استاتیک هستند. اگرچه همیشه اینطور نیست، اما عموماً نیروی اصطکاک اغلب با حرکت یک جسم مخالف است. برای مثال، اگر کتابی روی سطح میز بلغزد، میز در خلاف جهت حرکت خود نیروی اصطکاک وارد می‌کند. اصطکاک ناشی از فشرده شدن دو سطح به یکدیگر است که باعث ایجاد نیروهای جاذبه بین مولکول‌های سطوح مختلف می‌شود. به این ترتیب، اصطکاک به ماهیت دو سطح و میزان فشرده شدن آن‌ها به یکدیگر نیز بستگی دارد. حداکثر نیروی اصطکاک که یک سطح می‌تواند بر یک جسم وارد کند را می‌توان با استفاده از فرمول زیر محاسبه کرد:

$$F_{frict}=\mu . F_{Norm}$$

عوامل موثر بر نیروی اصطکاک

حرکت دوچرخه در جاده مسطح بسیار راحت‌تر از حرکت آن در جاده‌ای غیر مسطح است. سوالی که مطرح می‌شود آن است که آیا نیروی اصطکاک به زبری سطوح مربوط است؟ برای پاسخ به این پرسش به مثال زیر توجه کنید.

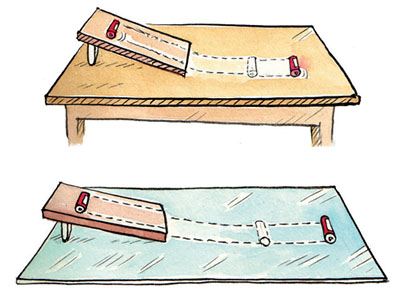
مطابق شکل زیر صفحه‌ای را به صورت شیب‌دار بر روی میز قرار دهید. سپس مدادی را بر روی خط نشان داده شده نگه دارید. اکنون مداد را رها کنید. مشاهده می‌کنید مداد پس از عبور از سطح شیب‌دار، در فاصله معینی از سطح بر روی میز متوقف می‌شود.

آزمایش بالا را بر روی میز شیشه‌ای تکرار کنید و به مسافت طی شده توسط مداد در این حالت دقت کنید. اکنون آزمایش را با پوشاندن سطح میز با لایه یکنواختی از شن تکرار کنید. مشاهده می‌کنید که مسافت طی شده توسط مداد بر روی سطح شیشه بیشینه و بر روی لایه شن کمینه است. این تفاوت به دلیل نیروی اصطکاک اعمالی از طرف سطوح مختلف بر مداد خواهد بود. در واقع نیروی اصطکاک کمتری از طرف سطح شیشه‌ای بر مداد وارد می‌شود. بنابراین، میزان صاف بودن سطوح یکی از عامل‌های موثر بر اصطکاک است.

نیروی مقاومت هوا $$F_{air}$$

نیروی مقاومت هوا نوع خاصی از نیروی اصطکاک است که بر روی اجسام هنگام حرکت در هوا تأثیر می‌گذارد. نیروی مقاومت هوا اغلب برای مخالفت با حرکت یک جسم مشاهده می‌شود. این نیرو به دلیل اندازه ناچیز آن (و به دلیل اینکه پیش بینی مقدار آن از نظر ریاضی دشوار است) اغلب نادیده گرفته می‌شود. این نیرو برای اجسامی که با سرعت بالا حرکت می‌کنند (مانند چترباز یا اسکی باز) یا برای اجسامی با سطح بزرگ بیشتر قابل توجه است.

نیروی کششی $$F_{tens}$$

نیروی کششی نیرویی است که از طریق یک ریسمان، طناب، کابل یا سیم، هنگامی که یک جسم توسط نیروهایی که از دو طرف مخالف وارد می‌شوند، منتقل می‌شود. نیروی کشش در طول سیم امتداد می‌یابد و به طور مساوی بر روی اجسام در انتهای مخالف سیم اثر می‌گذارد.

نیروی فنر $$F_{spring}$$

نیروی فنر نیرویی است که توسط یک فنر فشرده شده یا کشیده شده به هر جسمی که به آن متصل است وارد می‌شود. جسمی که فنر را فشرده یا کشیده می‌کند همیشه با نیرویی فنر که می‌خواهد آن را به حالت تعادل بازگرداند، مخالفت می‌کند. برای اکثر فنرها، مخصوصاً آن‌هایی که از قانون هوک پیروی می‌کنند، بزرگی نیرو با مقدار کشش یا فشرده سازی فنر نسبت مستقیم دارد.

نیروی مغناطیسی

نیروی وارد شده از طرف آهن‌ربا نیروی مغناطیسی نامیده می‌شود. به طور مثال، قطب‌های هم‌نام آهن‌ربا یکدیگر را دفع، درحالی‌که قطب‌های مخالف یکدیگر را جذب می‌کنند. نیروهای مغناطیسی بدون تماس بین دو آهن‌ربا وجود دارند.

نیروی الکترواستاتیکی

نیروی وارد شده از طرف اجسام باردار نیروی الکترواستاتیکی نامیده می‌شود. همانند نیروی مغناطیسی، نیروی الکترواستاتیکی نیز بدون تماس بین دو جسم وجود دارد.

در جدول زیر مثال‌هایی را از اندازه نیروهای مختلف در طبیعت مشاهده می‌کنید.

نقش نیرو‌های تعادلی و غیرتعادلی در مفهوم نیرو چیست ؟

تا اینجا می‌دانیم مفهوم نیرو چیست و با انواع نیروهای موجود در طبیعت آشنا شدیم. در ادامه تعریف نیروی تعادلی و غیرتعادلی و چگونگی تشخیص آنها را یاد خواهیم گرفت.

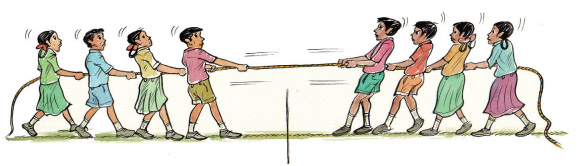
به هنگام شرکت در مسابقه طناب‌کشی تمام سعی خود را به کار خواهید برد تا نیروی بیشتری وارد کنید. در این مسابقه اگر دو گروه شرکت‌کننده نیروی یکسانی را بر طناب وارد کنند، تیم برنده‌ای وجود نخواهد داشت. هنگامی که یکی از دو تیم نیروی بزرگ‌تری را بر طناب وارد کند، تیم ضعیف‌تر به سمت تیم قوی‌تر حرکت می‌کند و بازنده بازی محسوب خواهد شد.

مثال نیروی تعادلی و غیر تعادلی

به منظور درک بهتر نیروهای تعادلی و غیرتعادلی، مثال زیر را در نظر بگیرید.

آجری را بر روی میزی قرار دهید. با دست راستتان آجر را به سمت چپ حرکت دهید. مشاهده می‌کنید که آجر به سمت چپ حرکت می‌کند. اکنون با دست چپ آجر را به سمت راست حرکت دهید. در این حالت آجر به سمت راست حرکت خواهد کرد. سپس دو دست را در دو طرف آجر قرار دهید و نیروهای مساوی به آن وارد کنید. آیا آجر حرکت می‌کند؟ مشاهده خواهید کرد که آجر در هیچ جهتی حرکت نمی‌کند. در واقع نیروهای وارد شده از سمت دو دست با یکدیگر در تعادل هستند. به چنین نیروهایی،‌ نیروهایی تعادلی می‌گویند.

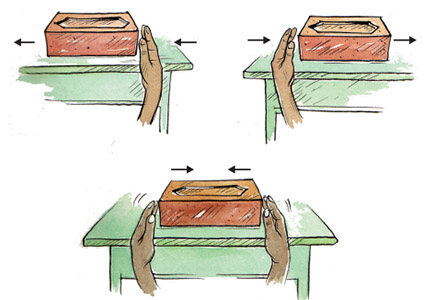
همان‌طور که در مثال بالا دیدیم نیروهای تعادلی تغییری در حالت سکون جسم یا حرکت آن ایجاد نمی‌کنند. حال این سوال مطرح می‌شود که اگر اندازه دو نیروی وارد شده بر آجر برابر نباشد چه اتفاقی رخ می‌دهد. در این حالت آجر در جهت نیروی بزرگ‌تر حرکت خواهد کرد. به چنین نیروهایی، نیروهای غیرتعادلی می‌گویند. نیروهای غیرتعادلی وارد بر یک جسم موجب حرکت جسم از حالت سکون یا تغییر حرکت جسم متحرک می‌شوند. تا اینجا یاد گرفتیم که نقش نیروهای تعادلی و غیرتعادلی در مفهوم نیرو چیست اما در ادامه قصد داریم با قوانین نیوتن آشنا شویم.

قوانین نیوتن چیست ؟

در ادامه به منظور داشتن درک بهتری از پرسش نیرو چیست به بیان قوانین نیوتن و کاربردهای آن‌ها در حرکت اجسام می‌پردازیم.

اینرسی چیست ؟

اینرسی تمایل اجسام برای حفظ حالت سکون یا حرکت با سرعت ثابت است. مثال‌های مختلفی از اینرسی را می‌توانید در زندگی روزمره بیابید. به طور مثال، دونده حتی پس از عبور از خط پایان باز هم به دلیل اینرسی به دویدن خود تا مسافتی مشخص ادامه می‌‌دهد. یاد گرفتیم که مفهوم اینرسی در نیرو چیست.

جرم چیست ؟ 

به مقدار ماده موجود در جسم جرم گفته می‌شود. هر چیزی که در اطرافمان مشاهده می‌کنیم دارای جرم است. در واقع وقتی می‌گوییم جسمی سبک‌ یا سنگین است به مقدار جرم آ‌ن‌ها اشاره می‌کنیم.

قانون اول نیوتن چیست ؟

آشنایی با قانون‌های نیوتن به ما در درک مفهوم نیرو چیست بسیار کمک خواهد کرد در نتیجه در ادامه به اختصار با این قوانین آشنا می‌شویم.

نیوتن ادعا کرد اجسام ساکن یا اجسام در حال حرکت با سرعت ثابت بر خط راست، در غیاب اثر خارجی در این حالت باقی خواهند ماند.

قانون اول نیوتن دارای کاربردهای بسیاری در زندگی روزمره است. هنگامی که در اتوبوس ساکن ایستاده‌اید و ناگهان اتوبوس شروع به حرکت می‌کند، شما به سمت عقب هل داده می‌شوید. در واقع پاهای شما در تماس با کف اتوبوس است. حرکت ناگهانی اتوبوسی سبب حرکت پاها با آن خواهد شد. ولی به دلیل اینرسی، قسمت بالای بدن تمایل به حفظ حالت سکون و افتادن به سمت عقب دارد.

قانون دوم نیوتن چیست ؟

بر طبق قانون اول نیوتن، اعمال نیروی غیرتعادلی بر جسم سبب تغییر در سرعت جسم خواهد شد. تغییر در سرعت به معنای شتاب است. در نتیجه، این قانون رابطه بین نیرو و شتاب را به صورت زیر بیان می‌کند.

$$F=ma$$

قانون سوم نیوتن چیست ؟

هنگامی که بادکنک پر شده از هوایی را رها می‌کنید، جهت حرکت بادکنک در خلاف جهت هوای خروجی از آن است.

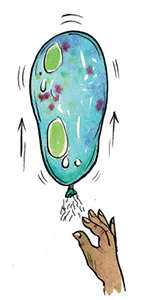
نیوتن در قانون سوم خود به رابطه بین عمل و عکس‌العمل پرداخت. بر طبق این قانون، برای هر عمل، عکس‌العمل مساوی و در خلاف جهتی وجود دارد. نیروهای عمل و عکس‌العمل بر دو جسم متفاوت وارد می‌شوند.

نمودار جسم آزاد

پس از آشنایی با مفهوم نیرو و انواع نیروهای موجود در طبیعت، اکنون به تحلیل نیروهای وارد شده بر جسم و چگونگی رسم آن‌ها می‌پردازیم.

به منظور تحلیل نیروهای وارد بر جسم از نمودار جسم آزاد استفاده می‌شود. نمودار جسم آزاد نموداری است که در آن اندازه‌های نسبی و جهت تمامی نیروهای وارد شده بر جسم رسم می‌شوند. این نمودار مثالی از نمودارهای برداری است. این نمودار از یک سیستم یگانه (جسم آزاد که می‌تواند جسم تک یا گروهی از اجسام باشد، تشکیل شده است. بردارهای رسم شده از جسم آزاد& نشان دهنده جهت و اندازه نیروهای وارد شده بر آن است. به منظور ترسیم صحیح نمودار جسم آزاد قانون‌های زیر را در نظر بگیرید.

• این نمودار تنها شامل سیستم ایزوله است. سیستم ایزوله می‌تواند از یک جسم یا تعداد زیادی اجسام تشکیل شده باشد، اما نیروهای وارد شده تنها بر این سیستم اعمال خواهند شد.
• بردارهای نیرو باید نیروهای واقعی (نیروهای گفته شده در بالا) باشند.
• فقط نیروهای وارد شده بر سیستم (نه نیروهای اعمال شده توسط سیستم) رسم می‌شوند.

فرض کنید دو فرد با یکدیگر مسابقه طناب‌کشی می‌دهند. اگر نیروهای وارد شده بر این دو فرد یکسان باشد، کدام‌یک از آن‌ها برنده مسابقه خواهد شد؟ نمودار جسم آزاد را بر یکی از این دو فرد به صورت زیر رسم می‌کنیم.

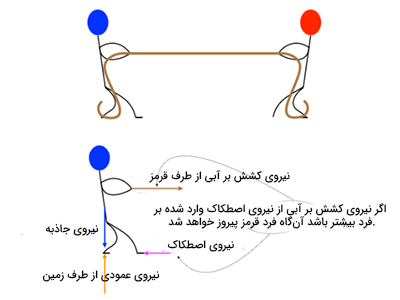
همان‌طور که در توضیحات بالا گفته شد می‌دانیم که در این مسابقه نقش نیرو چیست و نیروی وارد شده از سمت طناب بر هر دو فرد آبی و قرمز برابر است. سوالی که مطرح می‌شود آن است که آیا این دو نیرو یکدیگر را خنثی می‌کنند؟ پاسخ به این پرسش خیر است، زیرا این دو نیرو بر دو سیستم جداگانه وارد می‌شوند. به منظور رسم نمودار جسم آزاد، یکی از دو فرد آبی یا قرمز (در اینجا آبی) را در نظر می‌گیریم و نیروهای وارد شده بر این شخص را رسم می‌کنیم.

اگر تفریق برداری نیروهای افقی بر فرد آبی غیر صفر و برآیند آن‌ها به سمت چپ باشد، فرد آبی پیروز مسابقه خواهد بود. در نتیجه، نیروی اصطکاک وارد شده از سمت زمین بر فرد آبی باید بیشتر از نیروی کشش وارد شده بر او از سمت فرد قرمز باشد.

معرفی فیلم آموزش فیزیک پایه 1

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک پایه ۱ کرده است. این مجموعه آموزشی از سیزده درس تشکیل شده و برای دانشجویان رشته‌های علوم پایه و فنی و مهندسی مفید است. پیش‌نیاز این درس آموزش ریاضی عمومی ۱ است. این آموزش جزو اولین دروس دانشگاهی است که شامل مفاهیم مربوط به فیزیک عمومی است و اگر شما در مفاهیم ابتدایی فیزیک دچار مشکل هستید، پیشنهاد می‌کنیم از این آموزش شروع کنید و سپس مجموعه‌های دیگر مربوط به فیزیک را مشاهده کنید.

درس اول این مجموعه به اندازه گیری و یکاها و درس دوم به قوانین بردارها می‌پردازد. درس سوم به حرکت در یک بُعد و درس چهارم به حرکت در دو و سه‌بُعد اختصاص دارد. در درس پنجم و ششم به ترتیب دینامیک حرکت و کاربرد قوانین نیوتن و کار و انرژی را خواهید آموخت و با مفهوم نیرو چیست به خوبی آشنا خواهید چیست. در درس هفتم مفاهیم مربوط به پایستگی انرژی و انرژی پتانسیل بررسی می‌شود. در درس هشتم درباره تکانه و برخورد خواهید آموخت و درس نهم به مرکز جرم و سیستم‌های ذرات اختصاص دارد. درس دهم و یازدهم مباحث مربوط به سینماتیک و دینامیک دورانی را پوشش می‌دهد و درس دوازدهم و سیزدهم به مفاهیم مربوط به تکانه زاویه‌ای و تعادل اختصاص دارد.

• برای دیدن آموزش فیزیک پایه ۱ +‌ اینجا کلیک کنید.

جمع‌بندی

در این مطلب یاد گرفتیم نیرو چیست و در ادامه با بحث‌های زیر به اختصار آشنا شدیم.

• نیرو و کاربردهای آن در زندگی روزمره
• دسته بندی نیروها به دو گروه نیروهای تماسی و غیر تماسی
• نیروهای تعادلی و غیرتعادلی
• قوانین نیوتن